solving uniform motion problems

About me and why I created this physics website.

Uniform Motion Problems

• Search Website

Real World Applications — for high school level and above

• Amusement Parks
• Battle & Weapons
• Engineering
• Miscellaneous

Education & Theory — for high school level and above

• Useful Formulas
• Physics Questions
• Example Mechanics Problems
• Learn Physics Compendium

Kids Section

• Physics For Kids
• Science Experiments
• Science Fair Ideas
• Science Quiz
• Science Toys
• Teacher Resources
• Commercial Disclosure
• Privacy Policy

© Copyright 2009-2024 real-world-physics-problems.com

Physics Problems with Solutions

Motion problems, questions with solutions and tutorials.

Free questions and problems related to the SAT test and tutorials on rectilinear motion with either uniform velocity or uniform acceleration are included. The concepts of displacement, distance, velocity, speed, acceleration are thoroughly discussed. Problems, questions and examples are presented with solutions and detailed explanations. Graphical analysis of motion problems are also included.

Projectile Equations, Problems and Solutions

• Projectile Problems with Solutions and Explanations
• Solutions and Explanations to Projectile Problems
• Projectile Equations with Explanations

Distance and Displacement

• Displacement and Distance: Tutorials with Examples
• Displacement and Distance: Problems with Solutions

Velocity and Speed

• Velocity and Speed: Tutorials with Examples
• Velocity and Speed: Problems with Solutions

Uniform Acceleration

• Acceleration: Tutorials with Examples
• Uniform Acceleration Motion: Problems with Solutions
• Uniform Acceleration Motion: Equations with Explanations

Graphical Analysis of Motion

• Free SAT II Physics Practice Questions with Solutions on Graphical Analysis of Motion with detailed solutions

Formulas and Constants

• Physics Formulas Reference
• SI Prefixes Used with Units in Physics, Chemistry and Engineering
• Constants in Physics, Chemistry and Engineering

Popular Pages

• Privacy Policy

Algebra Motion Problems

In these lessons, we will learn how to solve algebra word problems that involve motion.

Related Pages Rate, Time and Distance Word Problems Rate, Time and Distance More Algebra Word Problems More Algebra Lessons

What are Motion or Distance Word Problems? Motion problems are based on the formula

where d = distance, r = rate and t = time.

How to solve Motion or Distance Word Problems? Step 1: Draw a diagram to represent the relationship between the distances involved in the problem. Step 2: Set up a chart based on the formula: rate × time = distance. Step 3: Use the chart to set up one or more equations. Step 4: Solve the equations.

We will look at three types of Motion Word Problems:

• Two objects going in opposite directions.
• Both objects going in the same direction, but one goes further.
• One object going and returning at different rates.

Solve Motion Word Problems: Two objects going in opposite directions

Example: John and Philip who live 14 miles apart start at noon to walk toward each other at rates of 3 mph and 4 mph respectively. After how many hours will they meet?

Solution: Let x = time walked.

3x + 4x = 14 7x = 14 x = 2

They will meet in 2 hours.

How to solve motion word problems with objects traveling in opposite directions?

Example: Two cars leave from the same place at the same time and travel in opposite direction. One car travels at 55 mph and the other at 75 mph. After how many hours will there be 520 miles apart?

Example: Two planes leave the same point at 8 AM. Plane 1 heads East at 600 mph and Plane 2 heads West at 450 mph. How long will they be 1400 miles apart? At what time will they be 1400 miles apart? How far has each plane traveled?

Solve Motion Word Problems: Two objects going in the same direction

Example: Aaron left L.A. to drive at 55 mph towards Las Vegas. Mike left L.A. an hour after Aaron (also towards Las Vegas), driving at 70 mph. How long will it take Mike to overtake Aaron?

How to solve motion word problems with objects traveling in the same direction?

Example: John left his house at 3.00 pm to drive 60 mph to drive towards Michigan. Phoebe left the same house at 5.00 pm, driving 80 mph in the same direction as John. How long will it take Phoebe to overtake John?

Solve Motion Word Problems: One object going and returning at different rates

Example: In still water, Peter’s boat goes 4 times as fast as the current in the river. He takes a 15-mile trip up the river and returns in 4 hours. Find the rate of the current.

Solution: Let x = rate of the current.

The rate of the current is 2 mph.

Example: Gordon rode his bike at 15 mph to get his car. He then drove back at 45 mph. If the entire trip took him 8 hours, how far away was his car?

Motion Word Problems This is how to set up motion problems for Algebra. Three Types of Problems

• Both going the same direction but one going further
• Two going in opposite directions
• Going in one direction and then returning at a different rate.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Classes (Version 2)
• Student Progress Edit
• Task Properties
• Export Student Progress
• Task, Activities, and Scores
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Tasks and Classes
• Tasks - Classic
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Task Tracker Directions
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Stoichiometry
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Motion in One Dimension
• Work, Energy and Power
• Algebra Based Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the CD
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Classes (Legacy Version)
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law
• Sample Problems and Solutions
• Kinematic Equations Introduction
• Solving Problems with Kinematic Equations
• Kinematic Equations and Free Fall
• Kinematic Equations and Kinematic Graphs

Check Your Understanding

Answer: d = 1720 m

Answer: a = 8.10 m/s/s

Answers: d = 33.1 m and v f = 25.5 m/s

Answers: a = 11.2 m/s/s and d = 79.8 m

Answer: t = 1.29 s

Answers: a = 243 m/s/s

Answer: a = 0.712 m/s/s

Answer: d = 704 m

Answer: d = 28.6 m

Answer: v i = 7.17 m/s

Answer: v i = 5.03 m/s and hang time = 1.03 s (except for in sports commericals)

Answer: a = 1.62*10 5 m/s/s

Answer: d = 48.0 m

Answer: t = 8.69 s

Answer: a = -1.08*10^6 m/s/s

Answer: d = -57.0 m (57.0 meters deep) 

Answer: v i = 47.6 m/s

Answer: a = 2.86 m/s/s and t = 30. 8 s

Answer: a = 15.8 m/s/s

Answer: v i = 94.4 mi/hr

Solutions to Above Problems

d = (0 m/s)*(32.8 s)+ 0.5*(3.20 m/s 2 )*(32.8 s) 2

Return to Problem 1

110 m = (0 m/s)*(5.21 s)+ 0.5*(a)*(5.21 s) 2

110 m = (13.57 s 2 )*a

a = (110 m)/(13.57 s 2 )

a = 8.10 m/ s 2

Return to Problem 2

d = (0 m/s)*(2.60 s)+ 0.5*(-9.8 m/s 2 )*(2.60 s) 2

d = -33.1 m (- indicates direction)

v f = v i + a*t

v f = 0 + (-9.8 m/s 2 )*(2.60 s)

v f = -25.5 m/s (- indicates direction)

Return to Problem 3

a = (46.1 m/s - 18.5 m/s)/(2.47 s)

a = 11.2 m/s 2

d = v i *t + 0.5*a*t 2

d = (18.5 m/s)*(2.47 s)+ 0.5*(11.2 m/s 2 )*(2.47 s) 2

d = 45.7 m + 34.1 m

(Note: the d can also be calculated using the equation v f 2 = v i 2 + 2*a*d)

Return to Problem 4

-1.40 m = (0 m/s)*(t)+ 0.5*(-1.67 m/s 2 )*(t) 2

-1.40 m = 0+ (-0.835 m/s 2 )*(t) 2

(-1.40 m)/(-0.835 m/s 2 ) = t 2

1.68 s 2 = t 2

Return to Problem 5

a = (444 m/s - 0 m/s)/(1.83 s)

a = 243 m/s 2

d = (0 m/s)*(1.83 s)+ 0.5*(243 m/s 2 )*(1.83 s) 2

d = 0 m + 406 m

Return to Problem 6

(7.10 m/s) 2 = (0 m/s) 2 + 2*(a)*(35.4 m)

50.4 m 2 /s 2 = (0 m/s) 2 + (70.8 m)*a

(50.4 m 2 /s 2 )/(70.8 m) = a

a = 0.712 m/s 2

Return to Problem 7

(65 m/s) 2 = (0 m/s) 2 + 2*(3 m/s 2 )*d

4225 m 2 /s 2 = (0 m/s) 2 + (6 m/s 2 )*d

(4225 m 2 /s 2 )/(6 m/s 2 ) = d

Return to Problem 8

d = (22.4 m/s + 0 m/s)/2 *2.55 s

d = (11.2 m/s)*2.55 s

Return to Problem 9

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(2.62 m)

0 m 2 /s 2 = v i 2 - 51.35 m 2 /s 2

51.35 m 2 /s 2 = v i 2

v i = 7.17 m/s

Return to Problem 10

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(1.29 m)

0 m 2 /s 2 = v i 2 - 25.28 m 2 /s 2

25.28 m 2 /s 2 = v i 2

v i = 5.03 m/s

To find hang time, find the time to the peak and then double it.

0 m/s = 5.03 m/s + (-9.8 m/s 2 )*t up

-5.03 m/s = (-9.8 m/s 2 )*t up

(-5.03 m/s)/(-9.8 m/s 2 ) = t up

t up = 0.513 s

hang time = 1.03 s

Return to Problem 11

(521 m/s) 2 = (0 m/s) 2 + 2*(a)*(0.840 m)

271441 m 2 /s 2 = (0 m/s) 2 + (1.68 m)*a

(271441 m 2 /s 2 )/(1.68 m) = a

a = 1.62*10 5 m /s 2

Return to Problem 12

• (NOTE: the time required to move to the peak of the trajectory is one-half the total hang time - 3.125 s.)

First use:  v f  = v i  + a*t

0 m/s = v i  + (-9.8  m/s 2 )*(3.13 s)

0 m/s = v i  - 30.7 m/s

v i  = 30.7 m/s  (30.674 m/s)

Now use:  v f 2  = v i 2  + 2*a*d

(0 m/s) 2  = (30.7 m/s) 2  + 2*(-9.8  m/s 2 )*(d)

0 m 2 /s 2  = (940 m 2 /s 2 ) + (-19.6  m/s 2 )*d

-940  m 2 /s 2  = (-19.6  m/s 2 )*d

(-940  m 2 /s 2 )/(-19.6  m/s 2 ) = d

Return to Problem 13

-370 m = (0 m/s)*(t)+ 0.5*(-9.8 m/s 2 )*(t) 2

-370 m = 0+ (-4.9 m/s 2 )*(t) 2

(-370 m)/(-4.9 m/s 2 ) = t 2

75.5 s 2 = t 2

Return to Problem 14

(0 m/s) 2 = (367 m/s) 2 + 2*(a)*(0.0621 m)

0 m 2 /s 2 = (134689 m 2 /s 2 ) + (0.1242 m)*a

-134689 m 2 /s 2 = (0.1242 m)*a

(-134689 m 2 /s 2 )/(0.1242 m) = a

a = -1.08*10 6 m /s 2

(The - sign indicates that the bullet slowed down.)

Return to Problem 15

d = (0 m/s)*(3.41 s)+ 0.5*(-9.8 m/s 2 )*(3.41 s) 2

d = 0 m+ 0.5*(-9.8 m/s 2 )*(11.63 s 2 )

d = -57.0 m

(NOTE: the - sign indicates direction)

Return to Problem 16

(0 m/s) 2 = v i 2 + 2*(- 3.90 m/s 2 )*(290 m)

0 m 2 /s 2 = v i 2 - 2262 m 2 /s 2

2262 m 2 /s 2 = v i 2

v i = 47.6 m /s

Return to Problem 17

( 88.3 m/s) 2 = (0 m/s) 2 + 2*(a)*(1365 m)

7797 m 2 /s 2 = (0 m 2 /s 2 ) + (2730 m)*a

7797 m 2 /s 2 = (2730 m)*a

(7797 m 2 /s 2 )/(2730 m) = a

a = 2.86 m/s 2

88.3 m/s = 0 m/s + (2.86 m/s 2 )*t

(88.3 m/s)/(2.86 m/s 2 ) = t

t = 30. 8 s

Return to Problem 18

( 112 m/s) 2 = (0 m/s) 2 + 2*(a)*(398 m)

12544 m 2 /s 2 = 0 m 2 /s 2 + (796 m)*a

12544 m 2 /s 2 = (796 m)*a

(12544 m 2 /s 2 )/(796 m) = a

a = 15.8 m/s 2

Return to Problem 19

v f 2 = v i 2 + 2*a*d

(0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(91.5 m)

0 m 2 /s 2 = v i 2 - 1793 m 2 /s 2

1793 m 2 /s 2 = v i 2

v i = 42.3 m/s

Now convert from m/s to mi/hr:

v i = 42.3 m/s * (2.23 mi/hr)/(1 m/s)

v i = 94.4 mi/hr

Return to Problem 20

6.2 Uniform Circular Motion

Section learning objectives.

By the end of this section, you will be able to do the following:

• Describe centripetal acceleration and relate it to linear acceleration
• Describe centripetal force and relate it to linear force
• Solve problems involving centripetal acceleration and centripetal force

Teacher Support

The learning objectives in this section will help your students master the following standards:

• (C) analyze and describe accelerated motion in two dimensions using equations, including projectile and circular examples.
• (D) calculate the effect of forces on objects, including the law of inertia, the relationship between force and acceleration, and the nature of force pairs between objects.

In addition, the High School Physics Laboratory Manual addresses content in this section in the lab titled: Circular and Rotational Motion, as well as the following standards:

Section Key Terms

Centripetal acceleration.

[BL] [OL] Review uniform circular motion. Ask students to give examples of circular motion. Review linear acceleration.

In the previous section, we defined circular motion . The simplest case of circular motion is uniform circular motion , where an object travels a circular path at a constant speed . Note that, unlike speed, the linear velocity of an object in circular motion is constantly changing because it is always changing direction. We know from kinematics that acceleration is a change in velocity , either in magnitude or in direction or both. Therefore, an object undergoing uniform circular motion is always accelerating, even though the magnitude of its velocity is constant.

You experience this acceleration yourself every time you ride in a car while it turns a corner. If you hold the steering wheel steady during the turn and move at a constant speed, you are executing uniform circular motion. What you notice is a feeling of sliding (or being flung, depending on the speed) away from the center of the turn. This isn’t an actual force that is acting on you—it only happens because your body wants to continue moving in a straight line (as per Newton’s first law) whereas the car is turning off this straight-line path. Inside the car it appears as if you are forced away from the center of the turn. This fictitious force is known as the centrifugal force . The sharper the curve and the greater your speed, the more noticeable this effect becomes.

[BL] [OL] [AL] Demonstrate circular motion by tying a weight to a string and twirling it around. Ask students what would happen if you suddenly cut the string? In which direction would the object travel? Why? What does this say about the direction of acceleration? Ask students to give examples of when they have come across centripetal acceleration.

Figure 6.7 shows an object moving in a circular path at constant speed. The direction of the instantaneous tangential velocity is shown at two points along the path. Acceleration is in the direction of the change in velocity; in this case it points roughly toward the center of rotation. (The center of rotation is at the center of the circular path). If we imagine Δ s Δ s becoming smaller and smaller, then the acceleration would point exactly toward the center of rotation, but this case is hard to draw. We call the acceleration of an object moving in uniform circular motion the centripetal acceleration a c because centripetal means center seeking .

Consider Figure 6.7 . The figure shows an object moving in a circular path at constant speed and the direction of the instantaneous velocity of two points along the path. Acceleration is in the direction of the change in velocity and points toward the center of rotation. This is strictly true only as Δ s Δ s tends to zero.

Now that we know that the direction of centripetal acceleration is toward the center of rotation, let’s discuss the magnitude of centripetal acceleration. For an object traveling at speed v in a circular path with radius r , the magnitude of centripetal acceleration is

Centripetal acceleration is greater at high speeds and in sharp curves (smaller radius), as you may have noticed when driving a car, because the car actually pushes you toward the center of the turn. But it is a bit surprising that a c is proportional to the speed squared. This means, for example, that the acceleration is four times greater when you take a curve at 100 km/h than at 50 km/h.

We can also express a c in terms of the magnitude of angular velocity . Substituting v = r ω v = r ω into the equation above, we get a c = ( r ω ) 2 r = r ω 2 a c = ( r ω ) 2 r = r ω 2 . Therefore, the magnitude of centripetal acceleration in terms of the magnitude of angular velocity is

Tips For Success

The equation expressed in the form a c = rω 2 is useful for solving problems where you know the angular velocity rather than the tangential velocity.

Virtual Physics

Ladybug motion in 2d.

In this simulation, you experiment with the position, velocity, and acceleration of a ladybug in circular and elliptical motion. Switch the type of motion from linear to circular and observe the velocity and acceleration vectors. Next, try elliptical motion and notice how the velocity and acceleration vectors differ from those in circular motion.

Grasp Check

In uniform circular motion, what is the angle between the acceleration and the velocity? What type of acceleration does a body experience in the uniform circular motion?

• The angle between acceleration and velocity is 0°, and the body experiences linear acceleration.
• The angle between acceleration and velocity is 0°, and the body experiences centripetal acceleration.
• The angle between acceleration and velocity is 90°, and the body experiences linear acceleration.
• The angle between acceleration and velocity is 90°, and the body experiences centripetal acceleration.

Centripetal Force

[BL] [OL] [AL] Using the same demonstration as before, ask students to predict the relationships between the quantities of angular velocity, centripetal acceleration, mass, centripetal force. Invite students to experiment by using various lengths of string and different weights.

Because an object in uniform circular motion undergoes acceleration (by changing the direction of motion but not the speed), we know from Newton’s second law of motion that there must be a net external force acting on the object. Since the magnitude of the acceleration is constant, so is the magnitude of the net force, and since the acceleration points toward the center of the rotation, so does the net force.

Any force or combination of forces can cause a centripetal acceleration. Just a few examples are the tension in the rope on a tether ball, the force of Earth’s gravity on the Moon, the friction between a road and the tires of a car as it goes around a curve, or the normal force of a roller coaster track on the cart during a loop-the-loop.

The component of any net force that causes circular motion is called a centripetal force . When the net force is equal to the centripetal force, and its magnitude is constant, uniform circular motion results. The direction of a centripetal force is toward the center of rotation, the same as for centripetal acceleration. According to Newton’s second law of motion, a net force causes the acceleration of mass according to F net = m a . For uniform circular motion, the acceleration is centripetal acceleration: a = a c . Therefore, the magnitude of centripetal force, F c , is F c = m a c F c = m a c .

By using the two different forms of the equation for the magnitude of centripetal acceleration, a c = v 2 / r a c = v 2 / r and a c = r ω 2 a c = r ω 2 , we get two expressions involving the magnitude of the centripetal force F c F c . The first expression is in terms of tangential speed, the second is in terms of angular speed: F c = m v 2 r F c = m v 2 r and F c = m r ω 2 F c = m r ω 2 .

Both forms of the equation depend on mass, velocity, and the radius of the circular path. You may use whichever expression for centripetal force is more convenient. Newton’s second law also states that the object will accelerate in the same direction as the net force. By definition, the centripetal force is directed towards the center of rotation, so the object will also accelerate towards the center. A straight line drawn from the circular path to the center of the circle will always be perpendicular to the tangential velocity. Note that, if you solve the first expression for r , you get

From this expression, we see that, for a given mass and velocity, a large centripetal force causes a small radius of curvature—that is, a tight curve.

Watch Physics

Centripetal force and acceleration intuition.

This video explains why centripetal force, when it is equal to the net force and has constant magnitude, creates centripetal acceleration and uniform circular motion.

Misconception Alert

Some students might be confused between centripetal force and centrifugal force. Centrifugal force is not a real force but the result of an accelerating reference frame, such as a turning car or the spinning Earth. Centrifugal force refers to a fictional center fleeing force.

• The yoyo will fly inward in the direction of the centripetal force.
• The yoyo will fly outward in the direction of the centripetal force.
• The yoyo will fly to the left in the direction of the tangential velocity.
• The yoyo will fly to the right in the direction of the tangential velocity.

Solving Centripetal Acceleration and Centripetal Force Problems

To get a feel for the typical magnitudes of centripetal acceleration, we’ll do a lab estimating the centripetal acceleration of a tennis racket and then, in our first Worked Example, compare the centripetal acceleration of a car rounding a curve to gravitational acceleration. For the second Worked Example, we’ll calculate the force required to make a car round a curve.

Estimating Centripetal Acceleration

In this activity, you will measure the swing of a golf club or tennis racket to estimate the centripetal acceleration of the end of the club or racket. You may choose to do this in slow motion. Recall that the equation for centripetal acceleration is a c = v 2 r a c = v 2 r or a c = r ω 2 a c = r ω 2 .

• One tennis racket or golf club
• One ruler or tape measure
• Work with a partner. Stand a safe distance away from your partner as he or she swings the golf club or tennis racket.
• Describe the motion of the swing—is this uniform circular motion? Why or why not?
• Try to get the swing as close to uniform circular motion as possible. What adjustments did your partner need to make?
• Measure the radius of curvature. What did you physically measure?
• By using the timer, find either the linear or angular velocity, depending on which equation you decide to use.
• What is the approximate centripetal acceleration based on these measurements? How accurate do you think they are? Why? How might you and your partner make these measurements more accurate?

The swing of the golf club or racket can be made very close to uniform circular motion. For this, the person would have to move it at a constant speed, without bending their arm. The length of the arm plus the length of the club or racket is the radius of curvature. Accuracy of measurements of angular velocity and angular acceleration will depend on resolution of the timer used and human observational error. The swing of the golf club or racket can be made very close to uniform circular motion. For this, the person would have to move it at a constant speed, without bending their arm. The length of the arm plus the length of the club or racket is the radius of curvature. Accuracy of measurements of angular velocity and angular acceleration will depend on resolution of the timer used and human observational error.

Was it more useful to use the equation a c = v 2 r a c = v 2 r or a c = r ω 2 a c = r ω 2 in this activity? Why?

• It should be simpler to use a c = r ω 2 a c = r ω 2 because measuring angular velocity through observation would be easier.
• It should be simpler to use a c = v 2 r a c = v 2 r because measuring tangential velocity through observation would be easier.
• It should be simpler to use a c = r ω 2 a c = r ω 2 because measuring angular velocity through observation would be difficult.
• It should be simpler to use a c = v 2 r a c = v 2 r because measuring tangential velocity through observation would be difficult.

Worked Example

Comparing centripetal acceleration of a car rounding a curve with acceleration due to gravity.

A car follows a curve of radius 500 m at a speed of 25.0 m/s (about 90 km/h). What is the magnitude of the car’s centripetal acceleration? Compare the centripetal acceleration for this fairly gentle curve taken at highway speed with acceleration due to gravity ( g ).

Because linear rather than angular speed is given, it is most convenient to use the expression a c = v 2 r a c = v 2 r to find the magnitude of the centripetal acceleration.

Entering the given values of v = 25.0 m/s and r = 500 m into the expression for a c gives

To compare this with the acceleration due to gravity ( g = 9.80 m/s 2 ), we take the ratio a c / g = ( 1.25  m/s 2 ) / ( 9.80 m/s 2 ) = 0.128 a c / g = ( 1.25  m/s 2 ) / ( 9.80 m/s 2 ) = 0.128 . Therefore, a c = 0.128 g a c = 0.128 g , which means that the centripetal acceleration is about one tenth the acceleration due to gravity.

Frictional Force on Car Tires Rounding a Curve

• Calculate the centripetal force exerted on a 900 kg car that rounds a 600-m-radius curve on horizontal ground at 25.0 m/s.
• Static friction prevents the car from slipping. Find the magnitude of the frictional force between the tires and the road that allows the car to round the curve without sliding off in a straight line.
• If the car would slip if it were to be traveling any faster, what is the coefficient of static friction between the tires and the road? Could we conclude anything about the coefficient of static friction if we did not know whether the car could round the curve any faster without slipping?

Strategy and Solution for (a)

We know that F c = m v 2 r F c = m v 2 r . Therefore,

Strategy and Solution for (b)

The image above shows the forces acting on the car while rounding the curve. In this diagram, the car is traveling into the page as shown and is turning to the left. Friction acts toward the left, accelerating the car toward the center of the curve. Because friction is the only horizontal force acting on the car, it provides all of the centripetal force in this case. Therefore, the force of friction is the centripetal force in this situation and points toward the center of the curve.

Strategy and Solution for (c)

If the car is about to slip, the static friction is at its maximum value and f = μ s N = μ s m g f = μ s N = μ s m g . Solving for μ s μ s , we get μ s = 938 900 × 9.8 = 0.11 μ s = 938 900 × 9.8 = 0.11 . Regardless of whether we know the maximum allowable speed for rounding the curve, we can conclude this is a minimum value for the coefficient.

Since we found the force of friction in part (b), we could also solve for the coefficient of friction, since f = μ s N = μ s m g f = μ s N = μ s m g . The static friction is only equal to μ s N μ s N when it is at the maximum possible value. If the car could go faster, the friction at the given speed would still be the same as we calculated, but the coefficient of static friction would be larger.

Practice Problems

Calculate the centripetal acceleration of an object following a path with a radius of a curvature of 0.2 m and at an angular velocity of 5 rad/s.

Check Your Understanding

• Uniform circular motion is when an object accelerates on a circular path at a constantly increasing velocity.
• Uniform circular motion is when an object travels on a circular path at a variable acceleration.
• Uniform circular motion is when an object travels on a circular path at a constant speed.
• Uniform circular motion is when an object travels on a circular path at a variable speed.

Which of the following is centripetal acceleration?

• The acceleration of an object moving in a circular path and directed radially toward the center of the circular orbit
• The acceleration of an object moving in a circular path and directed tangentially along the circular path
• The acceleration of an object moving in a linear path and directed in the direction of motion of the object
• The acceleration of an object moving in a linear path and directed in the direction opposite to the motion of the object
• Yes, the object is accelerating, so a net force must be acting on it.
• Yes, because there is no acceleration.
• No, because there is acceleration.
• No, because there is no acceleration.

Identify two examples of forces that can cause centripetal acceleration.

• The force of Earth’s gravity on the moon and the normal force
• The force of Earth’s gravity on the moon and the tension in the rope on an orbiting tetherball
• The normal force and the force of friction acting on a moving car
• The normal force and the tension in the rope on a tetherball

Use the Check Your Understanding questions to assess whether students master the learning objectives of this section. If students are struggling with a specific objective, the formative assessment will help identify which objective is causing the problem and direct students to the relevant content.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute Texas Education Agency (TEA). The original material is available at: https://www.texasgateway.org/book/tea-physics . Changes were made to the original material, including updates to art, structure, and other content updates.

Access for free at https://openstax.org/books/physics/pages/1-introduction

• Authors: Paul Peter Urone, Roger Hinrichs
• Publisher/website: OpenStax
• Book title: Physics
• Publication date: Mar 26, 2020
• Location: Houston, Texas
• Book URL: https://openstax.org/books/physics/pages/1-introduction
• Section URL: https://openstax.org/books/physics/pages/6-2-uniform-circular-motion

© Jan 19, 2024 Texas Education Agency (TEA). The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Copyright © 1999-2020 themathlab.com

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.4: Applications of Linear Systems

• Last updated
• Save as PDF
• Page ID 18350

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Set up and solve applications involving relationships between numbers.
• Set up and solve applications involving interest and money.
• Set up and solve mixture problems.
• Set up and solve uniform motion problems (distance problems).

Problems Involving Relationships between Real Numbers

We now have the techniques needed to solve linear systems. For this reason, we are no longer limited to using one variable when setting up equations that model applications. If we translate an application to a mathematical setup using two variables, then we need to form a linear system with two equations.

Example \(\PageIndex{1}\)

The sum of two numbers is \(40\) and their difference is \(8\). Find the numbers.

Identify variables:

Let \(x\) represent one of the unknown numbers.

Let \(y\) represent the other unknown number.

Set up equations :

When using two variables, we need to set up two equations. The first key phrase, “the sum of the two numbers is \(40\),” translates as follows:

And the second key phrase, “the difference is \(8\),” leads us to the second equation:

Therefore, our algebraic setup consists of the following system:

\(\left\{\begin{aligned} x+y&=40 \\ x-y&=8 \end{aligned}\right.\)

We can solve the resulting system using any method of our choosing. Here we choose to solve by elimination. Adding the equations together eliminates the variable \(y\).

\(\begin{aligned} x\color{red}{+y}&=40 \\ \underline{+\quad x\color{red}{-y}}&\underline{=8} \\ 2x&=48 \\ x&=24 \end{aligned}\)

Once we have \(x\), back substitute to find \(y\).

\(\begin{aligned} x+y&=40 \\ \color{OliveGreen}{24}\color{black}{+y}&=40 \\ 24+y\color{Cerulean}{-24}&=40\color{Cerulean}{-24} \\ y&=16 \end{aligned}\)

The sum of the two numbers should be \(42\) and their difference \(8\).

\(\begin{aligned} 24+16&=40 \\ 24-16&=8 \end{aligned}\)

The two numbers are \(24\) and \(16\).

Example \(\PageIndex{2}\)

The sum of \(9\) times a larger number and twice a smaller is \(6\). The difference of \(3\) times the larger and the smaller is \(7\). Find the numbers.

Begin by assigning variables to the larger and smaller number.

Let \(x\) represent the larger number.

Let \(y\) represent the smaller number.

The first sentence describes a sum and the second sentence describes a difference.

This leads to the following system:

\(\left\{\begin{aligned} 9x+2y&=6\\3x-y&=7 \end{aligned}\right.\)

Solve using the elimination method. Multiply the second equation by \(2\) and add.

\(\left\{\begin{aligned} 9x+2y&=6 \\ 3x-y&=7 \end{aligned}\right. \stackrel{\times 2}{\Rightarrow} \left\{\begin{aligned} 9x+2y&=6\\ 6x-2y&=14 \end{aligned}\right.\)

\(\begin{aligned} 9x\color{red}{+2y}&=6\\ \underline{+\quad 6x\color{red}{-2y}}&\underline{=14} \\ 15x&=20 \\ x&=\frac{20}{15} \\ x&=\frac{4}{3} \end{aligned}\)

Back substitute to find \(y\).

The larger number is \(\frac{4}{3}\) and the smaller number is \(−3\).

Exercise \(\PageIndex{1}\)

The sum of two numbers is \(3\). When twice the smaller number is subtracted from \(6\) times the larger the result is \(22\). Find the numbers.

The two numbers are \(−\frac{1}{2}\) and \(\frac{7}{2}\).

Interest and Money Problems

In this section, the interest and money problems should seem familiar. The difference is that we will be making use of two variables when setting up the algebraic equations.

Example \(\PageIndex{3}\)

A roll of \(32\) bills contains only $\(5\) bills and $\(10\) bills. If the value of the roll is $\(220\), then how many of each bill are in the roll?

Begin by identifying the variables.

Let \(x\) represent the number of $\(5\) bills.

Let \(y\) represent the number of $\(10\) bills.

When using two variables, we need to set up two equations. The first equation is created from the fact that there are \(32\) bills.

The second equation sums the value of each bill: the total value is $\(220\).

$\(5\cdot x+\)$\(10\cdot y=\)$\(220\)

Present both equations as a system; this is our algebraic setup.

\(\left\{\begin{aligned} x+y&=32 \\ 5x+10y&=220 \end{aligned}\right.\)

Here we choose to solve by elimination, although substitution would work just as well. Eliminate \(x\) by multiplying the first equation by \(−5\).

Now add the equations together:

Once we have \(y\), the number of $\(10\) bills, back substitute to find \(x\).

\(\begin{aligned} x+y&=32 \\ x+\color{OliveGreen}{12}&=32 \\ x+12\color{Cerulean}{-12}&=32\color{Cerulean}{-12} \\ x&=20 \end{aligned}\)

There are twenty $\(5\) bills and twelve $\(10\) bills. The check is left to the reader.

Example \(\PageIndex{4}\)

A total of $\(6,300\) was invested in two accounts. Part was invested in a CD at a \(4\frac{1}{2}\)% annual interest rate and part was invested in a money market fund at a \(3\frac{3}{4}\)% annual interest rate. If the total simple interest for one year was $\(267.75\), then how much was invested in each account?

Let \(x\) represent the amount invested at \(4\frac{1}{2}\)%\(=4.5\)%\(=0.045\)

Let \(y\) represent the amount invested at \(3\frac{3}{4}\)%\(=3.75\)%\(=0.0375\)

The total amount in both accounts can be expressed as

\(x+y=6,300\)

To set up a second equation, use the fact that the total interest was $\(267.75\). Recall that the interest for one year is the interest rate times the principal \((I=prt=pr⋅1=pr)\). Use this to add the interest in both accounts. Be sure to use the decimal equivalents for the interest rates given as percentages.

\(\begin{array}{ccccc}{\color{Cerulean}{interest\:from\:the\:CD}}&{\color{Cerulean}{+}}&{\color{Cerulean}{interest\:from\:the\:fund}}&{\color{Cerulean}{=}}&{\color{Cerulean}{total\:interest}}\\{0.045x}&{+}&{0.375y}&{=}&{267.75} \end{array}\)

These two equations together form the following linear system:

\(\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.\)

Eliminate \(y\) by multiplying the first equation by \(−0.0375\).

\(\left\{\begin{aligned} x+y&=6,300 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right. \stackrel{\times (-0.0375)}{\Rightarrow} \left\{\begin{aligned} -0.0375x-0.0375y&=-236.25 \\ 0.045x+0.0375y&=267.75 \end{aligned}\right.\)

Next, add the equations together to eliminate the variable \(y\).

\(\begin{aligned} -0.0375x\color{red}{-0.0375y}&=-236.25 \\ \underline{+\quad 0.045x\color{red}{+0.0375y}}&\underline{=267.75} \\ 0.0075x&=31.5 \\ \frac{0.0075x}{\color{Cerulean}{0.0075}}&=\frac{31.5}{\color{Cerulean}{0.0075}} \\ x&=4,200 \end{aligned}\)

Back substitute.

\(\begin{aligned} x+y&=6,300 \\ \color{OliveGreen}{4,200}\color{black}{+y}&=6,300 \\ 4,200+y\color{Cerulean}{-4,200}&=6,300\color{Cerulean}{-4,200} \\ y&=2,100 \end{aligned}\)

$\(4,200\) was invested at \(4\frac{1}{2}\)% and $\(2,100\) was invested at \(3\frac{3}{4}\)%

At this point, we should be able to solve these types of problems in two ways: with one variable and now with two variables. Setting up word problems with two variables often simplifies the entire process, particularly when the relationships between the variables are not so clear.

Exercise \(\PageIndex{2}\)

On the first day of a two-day meeting, \(10\) coffees and \(10\) doughnuts were purchased for a total of $\(20.00\). Since nobody drank the coffee and all the doughnuts were eaten, the next day only \(2\) coffees and \(14\) doughnuts were purchased for a total of $\(13.00\). How much did each coffee and each doughnut cost?

Coffee: $\(1.25\); doughnut: $\(0.75\)

Mixture Problems

Mixture problems often include a percentage and some total amount. It is important to make a distinction between these two types of quantities. For example, if a problem states that a \(20\)-ounce container is filled with a \(2\)% saline (salt) solution, then this means that the container is filled with a mixture of salt and water as follows:

In other words, we multiply the percentage times the total to get the amount of each part of the mixture.

Example \(\PageIndex{5}\)

A \(2\)% saline solution is to be combined and mixed with a \(5\)% saline solution to produce \(72\) ounces of a \(2.5\)% saline solution. How much of each is needed?

Let \(x\) represent the amount of \(2\)% saline solution needed.

Let \(y\) represent the amount of \(5\)% saline solution needed.

The total amount of saline solution needed is \(72\) ounces. This leads to one equation,

The second equation adds up the amount of salt in the correct percentages. The amount of salt is obtained by multiplying the percentage times the amount, where the variables \(x\) and \(y\) represent the amounts of the solutions.

\(\begin{array}{ccccc}{\color{Cerulean}{salt\:in2\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{salt\:in\:5\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{salt\:in\:the\:end\:solution}}\\{0.02x}&{+}&{0.05y}&{=}&{0.025(72)}\end{array}\)

\(\left\{\begin{aligned} x+y&=72 \\ 0.02x+0.05y&=0.025(72) \end{aligned}\right. \stackrel{\times (-0.02)}{\Rightarrow} \left\{\begin{aligned} -0.02x-0.02y&=-1.44 \\ 0.02x+0.05y&=1.8 \end{aligned}\right.\)

\(\begin{aligned} \color{red}{-0.02x}\color{black}{-0.02y}&=-1.44 \\ \underline{+\quad\color{red}{0.02x}\color{black}{+0.05y}}&\underline{=1.8} \\ 0.03y&=0.36 \\ \frac{0.03y}{\color{Cerulean}{0.03}}&=\frac{0.36}{\color{Cerulean}{0.03}} \\ y&=12 \end{aligned}\)

\(\begin{aligned} x+y&=72 \\ x+\color{OliveGreen}{12}&=72 \\ x+12\color{Cerulean}{-12}&=72\color{Cerulean}{-12} \\ x&=60 \end{aligned}\)

We need \(60\) ounces of the \(2\)% saline solution and \(12\) ounces of the \(5\)% saline solution.

Example \(\PageIndex{6}\)

A \(50\)% alcohol solution is to be mixed with a \(10\)% alcohol solution to create an \(8\)-ounce mixture of a \(32\)% alcohol solution. How much of each is needed?

Let \(x\) represent the amount of \(50\)% alcohol solution needed.

Let \(y\) represent the amount of \(10\)% alcohol solution needed.

The total amount of the mixture must be \(8\) ounces.

The second equation adds up the amount of alcohol from each solution in the correct percentages. The amount of alcohol in the end result is \(32\)% of \(8\) ounces, or \(0.032(8)\).

\(\begin{array}{ccccc}{\color{Cerulean}{alcohol\:in\:50\%\:solution}}&{\color{Cerulean}{+}}&{\color{Cerulean}{alcohol\:in\:10\%\:solution}}&{\color{Cerulean}{=}}&{\color{Cerulean}{alcohol\:in\:the\:end\:solution}}\\{0.50x}&{+}&{0.10y}&{=}&{0.32(8)}\end{array}\)

Now we can form a system of two linear equations and two variables as follows:

\(\left\{\begin{aligned} x+y&=8 \\ 0.50x+0.10y&=0.32(8) \end{aligned}\right.\)

In this example, multiply the second equation by \(100\) to eliminate the decimals. In addition, multiply the first equation by \(−10\) to line up the variable \(y\) to eliminate.

\(\begin{array}{c|c} {Equation\:1:}&{Equation\:2:}\\{\color{Cerulean}{-10}\color{black}{(x+y)=}\color{Cerulean}{-10}\color{black}{(8)}}&{\color{Cerulean}{100}\:\color{black}{0.50x+0.10y=}\color{Cerulean}{100}\color{black}{(0.32)(8)}}\\{-10x-10y=-80}&{50x+10y=256} \end{array}\)

We obtain the following equivalent system:

Add the equations and then solve for \(x\):

\(\begin{aligned} x+y&=8 \\ \color{OliveGreen}{4.4}\color{black}{+y}&=8 \\ 4.4+y\color{Cerulean}{-4.4}&=8\color{Cerulean}{-4.4} \\ x&=3.6 \end{aligned}\)

To obtain \(8\) ounces of a \(32\)% alcohol mixture we need to mix \(4.4\) ounces of the \(50\)% alcohol solution and \(3.6\) ounces of the \(10\)% solution.

Exercise \(\PageIndex{3}\)

A \(70\)% antifreeze concentrate is to be mixed with water to produce a \(5\)-gallon mixture containing \(28\)% antifreeze. How much water and antifreeze concentrate is needed?

We need to mix \(3\) gallons of water with \(2\) gallons of antifreeze concentrate.

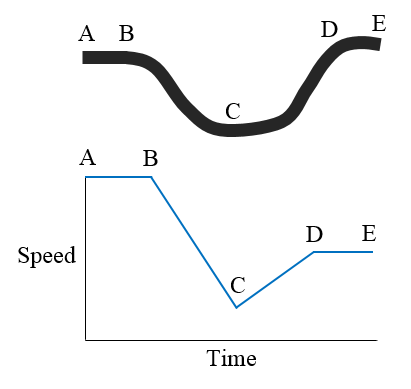
Uniform Motion Problems (Distance Problems)

Recall that the distance traveled is equal to the average rate times the time traveled at that rate, \(D=r⋅t\).

These uniform motion problems usually have a lot of data, so it helps to first organize that data in a chart and then set up a linear system. In this section, you are encouraged to use two variables.

Example \(\PageIndex{7}\)

An executive traveled a total of \(8\) hours and \(1,930\) miles by car and by plane. Driving to the airport by car, she averaged \(60\) miles per hour. In the air, the plane averaged \(350\) miles per hour. How long did it take her to drive to the airport?

We are asked to find the time it takes her to drive to the airport; this indicates that time is the unknown quantity.

Let \(x\) represent the time it took to drive to the airport.

Let \(y\) represent the time spent in the air.

Use the formula \(D=r⋅t\) to fill in the unknown distances.

\(\color{Cerulean}{Distance\:traveled\:in\:the\:car:}\quad\color{black}{D=r\cdot t=60\cdot x}\)

\(\color{Cerulean}{Distance\:traveled\:in\:the\:air:}\quad\color{black}{D=r\cdot t=350\cdot y}\)

The distance column and the time column of the chart help us to set up the following linear system.

\(\left\{\begin{aligned} x+y&=8 &\color{Cerulean}{\leftarrow\:total\:time\:traveled} \\ 6-x+350y&=1,930 &\color{Cerulean}{\leftarrow\:total\:distance\:traveled} \end{aligned}\right.\)

Now back substitute to find the time it took to drive to the airport \(x\):

\(\begin{aligned} x+y&=8 \\ x+\color{OliveGreen}{5}&=8 \\ x&=3 \end{aligned}\)

It took her \(3\) hours to drive to the airport.

It is not always the case that time is the unknown quantity. Read the problem carefully and identify what you are asked to find; this defines your variables.

Example \(\PageIndex{8}\)

Flying with the wind, an airplane traveled \(1,365\) miles in \(3\) hours. The plane then turned against the wind and traveled another \(870\) miles in \(2\) hours. Find the speed of the airplane and the speed of the wind.

There is no obvious relationship between the speed of the plane and the speed of the wind. For this reason, use two variables as follows:

Let \(x\) represent the speed of the airplane.

Let \(w\) represent the speed of the wind.

Use the following chart to organize the data:

With the wind, the airplane’s total speed is \(x+w\). Flying against the wind, the total speed is \(x−w\).

Use the rows of the chart along with the formula \(D=r⋅t\) to construct a linear system that models this problem. Take care to group the quantities that represent the rate in parentheses.

\(\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 &\color{Cerulean}{\leftarrow\:distance\:traveled\:with\:the\:wind} \\ 870&=(x-w)\cdot 2 &\color{Cerulean}{\leftarrow\:distance\:traveled\:against\:the\:wind} \end{aligned}\right.\)

If we divide both sides of the first equation by \(3\) and both sides of the second equation by \(2\), then we obtain the following equivalent system:

\(\left\{\begin{aligned} 1,365&=(x+w)\cdot 3 \\ 870&=(x-w)\cdot 2 \end{aligned}\right. \begin{aligned} &\stackrel{\div 3}{\Rightarrow} \\ &\stackrel{\div 2}{\Rightarrow} \end{aligned} \left\{\begin{aligned} 455&=x+w \\ 435&=x-w \end{aligned}\right.\)

\(\begin{aligned} x\color{red}{+w}&=455 \\ \underline{+\quad x\color{red}{-w}}&\underline{=435} \\ 2x&=890 \\ \frac{2x}{\color{Cerulean}{2}}&=\frac{890}{\color{Cerulean}{2}} \\ x&=455 \end{aligned}\)

\(\begin{aligned} x+w&=455 \\ \color{OliveGreen}{455}\color{black}{+w}&=455 \\ w&=10 \end{aligned}\)

The speed of the airplane is \(445\) miles per hour and the speed of the wind is \(10\) miles per hour.

Exercise \(\PageIndex{4}\)

A boat traveled \(24\) miles downstream in \(2\) hours. The return trip, which was against the current, took twice as long. What are the speeds of the boat and of the current?

The speed of the boat is \(9\) miles per hour and the speed of the current is \(3\) miles per hour.

Key Takeaways

• Use two variables as a means to simplify the algebraic setup of applications where the relationship between unknowns is unclear.
• Carefully read the problem several times. If two variables are used, then remember that you need to set up two linear equations in order to solve the problem.
• Be sure to answer the question in sentence form and include the correct units for the answer.

Exercise \(\PageIndex{5}\) Applications Involving Numbers

Set up a linear system and solve.

• The sum of two integers is \(54\) and their difference is \(10\). Find the integers.
• The sum of two integers is \(50\) and their difference is \(24\). Find the integers.
• The sum of two positive integers is \(32\). When the smaller integer is subtracted from twice the larger, the result is \(40\). Find the two integers.
• The sum of two positive integers is \(48\). When twice the smaller integer is subtracted from the larger, the result is \(12\). Find the two integers.
• The sum of two integers is \(74\). The larger is \(26\) more than twice the smaller. Find the two integers.
• The sum of two integers is \(45\). The larger is \(3\) less than three times the smaller. Find the two integers.
• The sum of two numbers is zero. When \(4\) times the smaller number is added to \(8\) times the larger, the result is \(1\). Find the two numbers.
• The sum of a larger number and \(4\) times a smaller number is \(5\). When \(8\) times the smaller is subtracted from twice the larger, the result is \(−2\). Find the numbers.
• The sum of \(12\) times the larger number and \(11\) times the smaller is \(−36\). The difference of \(12\) times the larger and \(7\) times the smaller is \(36\). Find the numbers.
• The sum of \(4\) times the larger number and \(3\) times the smaller is \(7\). The difference of \(8\) times the larger and \(6\) times the smaller is \(10\). Find the numbers.

1. The integers are \(22\) and \(32\).

3. The integers are \(8\) and \(24\).

5. The integers are \(16\) and \(58\).

7. The two numbers are \(−\frac{1}{4}\) and \(\frac{1}{4}\).

9. The smaller number is \(−4\) and the larger is \(\frac{2}{3}\).

Exercise \(\PageIndex{6}\) Interest and Money Problems

• A $\(7,000\) principal is invested in two accounts, one earning \(3\)% interest and another earning \(7\)% interest. If the total interest for the year is $\(262\), then how much is invested in each account?
• Mary has her total savings of $\(12,500\) in two different CD accounts. One CD earns \(4.4\)% interest and another earns \(3.2\)% interest. If her total interest for the year is $\(463\), then how much does she have in each CD account?
• Sally’s $\(1,800\) savings is in two accounts. One account earns \(6\)% annual interest and the other earns \(3\)%. Her total interest for the year is $\(93\). How much does she have in each account?
• Joe has two savings accounts totaling $\(4,500\). One account earns \(3\frac{3}{4}\)% annual interest and the other earns \(2\frac{5}{8}\)%. If his total interest for the year is $\(141.75\), then how much is in each account?
• Millicent has $\(10,000\) invested in two accounts. For the year, she earns $\(535\) more in interest from her \(7\)% mutual fund account than she does from her \(4\)% CD. How much does she have in each account?
• A small business has $\(85,000\) invested in two accounts. If the account earning \(3\)% annual interest earns $\(825\) more in interest than the account earning \(4.5\)% annual interest, then how much is invested in each account?
• Jerry earned a total of $\(284\) in simple interest from two separate accounts. In an account earning \(6\)% interest, Jerry invested $\(1,000\) more than twice the amount he invested in an account earning \(4\)%. How much did he invest in each account?
• James earned a total of $\(68.25\) in simple interest from two separate accounts. In an account earning \(2.6\)% interest, James invested one-half as much as he did in the other account that earned \(5.2\)%. How much did he invest in each account?
• A cash register contains $\(10\) bills and $\(20\) bills with a total value of $\(340\). If there are \(23\) bills total, then how many of each does the register contain?
• John was able to purchase a pizza for $\(10.80\) with quarters and dimes. If he uses \(60\) coins to buy the pizza, then how many of each did he have?
• Dennis mowed his neighbor’s lawn for a jar of dimes and nickels. Upon completing the job, he counted the coins and found that there were \(4\) less than twice as many dimes as there were nickels. The total value of all the coins is $\(6.60\). How many of each coin did he have?
• Two families bought tickets for the big football game. One family ordered \(2\) adult tickets and \(3\) children’s tickets for a total of $\(26.00\). Another family ordered \(3\) adult tickets and \(4\) children’s tickets for a total of $\(37.00\). How much did each adult ticket cost?
• Two friends found shirts and shorts on sale at a flea market. One bought \(5\) shirts and \(3\) shorts for a total of $\(51.00\). The other bought \(3\) shirts and \(7\) shorts for a total of $\(80.00\). How much was each shirt and each pair of shorts?
• On Monday Joe bought \(10\) cups of coffee and \(5\) doughnuts for his office at a cost of $\(16.50\). It turns out that the doughnuts were more popular than the coffee. Therefore, on Tuesday he bought \(5\) cups of coffee and \(10\) doughnuts for a total of $\(14.25\). How much was each cup of coffee?

1. $\(5,700\) at \(3\)% and $\(1,300\) at \(7\)%

3. $\(1,300\) at \(6\)% and $\(500\) at \(3\)%

5. $\(8,500\) at \(7\)% and $\(1,500\) at \(4\)%

7. $\(1,400\) at \(4\)% and $\(3,800\) at \(6\)%

9. \(12\) tens and \(11\) twenties

11. \(52\) dimes and \(28\) nickels

13. Shirts: $\(4.50\); shorts: $\(9.50\)

Exercise \(\PageIndex{7}\) Mixture Problems

• A \(15\)% acid solution is to be mixed with a \(25\)% acid solution to produce \(12\) gallons of a \(20\)% acid solution. How much of each is needed?
• One alcohol solution contains \(12\)% alcohol and another contains \(26\)% alcohol. How much of each should be mixed together to obtain \(5\) gallons of a \(14.8\)% alcohol solution?
• A nurse wishes to obtain \(40\) ounces of a \(1.2\)% saline solution. How much of a \(1\)% saline solution must she mix with a \(2\)% saline solution to achieve the desired result?
• A customer ordered \(20\) pounds of fertilizer that contains \(15\)% nitrogen. To fill the customer’s order, how much of the stock \(30\)% nitrogen fertilizer must be mixed with the \(10\)% nitrogen fertilizer?
• A customer ordered \(2\) pounds of a mixed peanut product containing \(15\)% cashews. The inventory consists of only two mixes containing \(10\)% and \(30\)% cashews. How much of each type must be mixed to fill the order?
• How many pounds of pure peanuts must be combined with a \(20\)% peanut mix to produce \(10\) pounds of a \(32\)% peanut mix?
• How much cleaning fluid with \(20\)% alcohol content, must be mixed with water to obtain a \(24\)-ounce mixture with \(10\)% alcohol content?
• A chemist wishes to create a \(32\)-ounce solution with \(12\)% acid content. He uses two types of stock solutions, one with \(30\)% acid content and another with \(10\)% acid content. How much of each does he need?
• A concentrated cleaning solution that contains \(50\)% ammonia is mixed with another solution containing \(10\)% ammonia. How much of each is mixed to obtain \(8\) ounces of a \(32\)% ammonia cleaning formula?
• A \(50\)% fruit juice concentrate can be purchased wholesale. Best taste is achieved when water is mixed with the concentrate in such a way as to obtain a \(12\)% fruit juice mixture. How much water and concentrate is needed to make a \(50\)-ounce fruit juice drink?
• A \(75\)% antifreeze concentrate is to be mixed with water to obtain \(6\) gallons of a \(25\)% antifreeze solution. How much water is needed?
• Pure sugar is to be mixed with a fruit salad containing \(10\)% sugar to produce \(48\) ounces of a salad containing \(16\)% sugar. How much pure sugar is required?

1. \(6\) gallons of each

3. \(32\) ounces of the \(1\)% saline solution and \(8\) ounces of the \(2\)% saline solution

5. \(1.5\) pounds of the \(10\)% cashew mix and \(0.5\) pounds of the \(30\)% cashew mix

7. \(12\) ounces of cleaning fluid

9. \(4.4\) ounces of the \(50\)% ammonia solution and \(3.6\) ounces of the \(10\)% ammonia solution

11. \(4\) gallons

Exercise \(\PageIndex{8}\) Uniform Motion Problems

• An airplane averaged \(460\) miles per hour on a trip with the wind behind it and \(345\) miles per hour on the return trip against the wind. If the total round trip took \(7\) hours, then how long did the airplane spend on each leg of the trip?
• The two legs of a \(330\)-mile trip took \(5\) hours. The average speed for the first leg of the trip was \(70\) miles per hour and the average speed for the second leg of the trip was \(60\) miles per hour. How long did each leg of the trip take?
• An executive traveled \(1,200\) miles, part by helicopter and part by private jet. The jet averaged \(320\) miles per hour while the helicopter averaged \(80\) miles per hour. If the total trip took \(4\frac{1}{2}\) hours, then how long did she spend in the private jet?
• Joe took two buses on the \(463\)-mile trip from San Jose to San Diego. The first bus averaged \(50\) miles per hour and the second bus was able to average \(64\) miles per hour. If the total trip took \(8\) hours, then how long was spent in each bus?
• Billy canoed downstream to the general store at an average rate of \(9\) miles per hour. His average rate canoeing back upstream was \(4\) miles per hour. If the total trip took \(6\frac{1}{2}\) hours, then how long did it take Billy to get back on the return trip?
• Two brothers drove the \(2,793\) miles from Los Angeles to New York. One of the brothers, driving in the day, was able to average \(70\) miles per hour, and the other, driving at night, was able to average \(53\) miles per hour. If the total trip took \(45\) hours, then how many hours did each brother drive?
• A boat traveled \(24\) miles downstream in \(2\) hours. The return trip took twice as long. What was the speed of the boat and the current?
• A helicopter flying with the wind can travel \(525\) miles in \(5\) hours. On the return trip, against the wind, it will take \(7\) hours. What are the speeds of the helicopter and of the wind?
• A boat can travel \(42\) miles with the current downstream in \(3\) hours. Returning upstream against the current, the boat can only travel \(33\) miles in \(3\) hours. Find the speed of the current.
• A light aircraft flying with the wind can travel \(180\) miles in \(1\frac{1}{2}\) hours. The aircraft can fly the same distance against the wind in \(2\) hours. Find the speed of the wind.

1. The airplane flew \(3\) hours with the wind and \(4\) hours against the wind.

3. \(3.5\) hours

5. \(4.5\) hours

7. Boat: \(9\) miles per hour; current: \(3\) miles per hour

9. \(1.5\) miles per hour

Exercise \(\PageIndex{9}\) Discussion Board

• Compose a number or money problem that can be solved with a system of equations of your own and share it on the discussion board.
• Compose a mixture problem that can be solved with a system of equations of your own and share it on the discussion board.
• Compose a uniform motion problem that can be solved with a system of equations of your own and share it on the discussion board

1. Answers may vary

3. Answers may vary