High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
Free ready-to-use math resources
Hundreds of free math resources created by experienced math teachers to save time, build engagement and accelerate growth


24 Ratio Word Problems for Grades 6-7 With Tips On Supporting Students’ Progress
Emma Johnson
Ratio word problems are introduced for the first time in 6th grade. The earliest mention of ‘Ratio’ is in the 6th grade Ratio and Proportional Relationships strand of the Common Core State Standards for math.
At this early stage, it is essential to concentrate on the language and vocabulary of ratio relationships. Children need to be clear on the meaning of the ratio symbol right from the start of the topic. Word problems really help children understand this concept since they make it much more relevant and meaningful than a ratio question with no context.
Concrete resources and visual representations are key to the success of children’s early understanding of ratio. These resources are often used in 2nd grade word problems , 3rd grade word problems and 4th grade word problems . There is often a misconception amongst upper elementary teachers and students, that mathematical manipulatives are only for children who struggle in math. However, all students should be introduced to this new concept through resources, such as two-sided counters and visual representations, such as bar models as this can help with understanding basic mathematical concepts such as addition and subtraction word problems .
As students progress across grades, they continue to build on their knowledge and understanding of ratio. This means that students gradually move away from the practical and visual resources, while word problems continue to be a key element to any lessons involving ratios. This foundational ratio knowledge is used as a base for proportional relationships and then linear relationships in later grades.
Ratio word problems are also an essential component of any lessons on ratio, to help children understand how ratios are used in real life.

Ratio Check for Understanding Quiz
10 questions with answers covering ratio to test your 6th and 7th grade student understanding of ratios.
Ratio word problems
Schools following CCSS
Ratios in 6th grade
Children are first introduced to ratio and ratio problems in 6th grade:
- Recognize and write ratio relationships using conventional math notation
- Recognize and write unit rate relationships using conventional math notation
- Create tables of equivalent ratios and use the tables to solve problems, including measurement problems
- Calculate unit rates and use unit rates to solve problems
- Recognize and write percents (a special type of ratio)
- Calculate a whole given a part or a percent *Note that all original ratio relationships in 6th grade involve only whole numbers – however students are expected to create equivalent ratios that involve fractions or decimals (particularly for unit rates)
Ratios in 7th grade
Students in 7th grade continue to build on their knowledge of ratio from 6th grade.
- Calculate unit rates and solve problems for ratios comparing two fractions
- Solve problems involving proportional relationships
- Solve problems involving percentage change, including: percentage increase, decrease and original value problems and simple interest in financial mathematics.
- Use scale factors to draw smaller or larger geometric figures
- Calculate the scale factor between two similar geometric figures
Schools not following CCSS
Schools that do not follow the Common Core will most likely cover the topics above but may do so in a different order or a different grade levels. Consult with your school’s specific curriculum map for clarification.
Why are word problems important for children’s understanding of ratio?
Solving word problems is important for helping children develop their understanding of ratio and the different ways ratio is used in everyday life. Without this context, ratio can be quite an abstract concept, which children find difficult to understand. Word problems bring ratios to life and enable students to see how they will make use of this skill outside the classroom.
Third Space Learning’s online one-on-one tutoring programs relate math concepts to real-world situations to deepen conceptual understanding. The online lessons are personalized to fill the gaps in each individual student’s math knowledge, helping them to build skills and confidence.
How to teach ratio word problem-solving in middle school
It is important that children learn the skills needed to solve ratio word problems. As with any math problem, children need to make sure they have read the questions carefully and thought about exactly what is being asked and whether they have fully understood this. The next step is to identify what they will need to do to solve the problem and whether there are any concrete resources or visual representations that will help them. Even older students can benefit from drawing a quick sketch to understand what a problem is asking.
Here is an example:
Jamie has a bag of red and yellow candies.
For every red candy, there are 2 yellow candies.
If the bag has 6 red candies, how many candies are in the whole bag?
How to solve:
What do you already know?
- We know that for every red candy, there are 2 yellow candies.
- If there are 6 red candies, we need to find how many yellow candies there must be.
- If there are 2 yellow candies for each 1 red candy, then we can multiply 2 by 6, to calculate how many yellow candies there are with 6 red candies.
- Once we have calculated the total number of yellow candies (12), we then need to add this to the 6 red candies, to work out how many candies are in the bag altogether.
- If there are 6 red candies and 12 yellow candies, there must be 18 candies in the bag altogether.
How can this be represented visually?

- We can use the two-sided counters to represent the red and yellow candies.
- We put down 1 red counter and 2 yellow counters.
- We then need to repeat this 6 times, until there are 6 red counters and 12 yellow counters.
- We can now visually see the answer to the word problem and that there are now a total of 18 counters (18 candies in the bag).
Ratio word problems for 6th grade
Word problems for 6th grade often incorporate multiple skills: a ratio word problem may also include elements from multiplication word problems , division word problems , percentage word problems and fraction word problems.
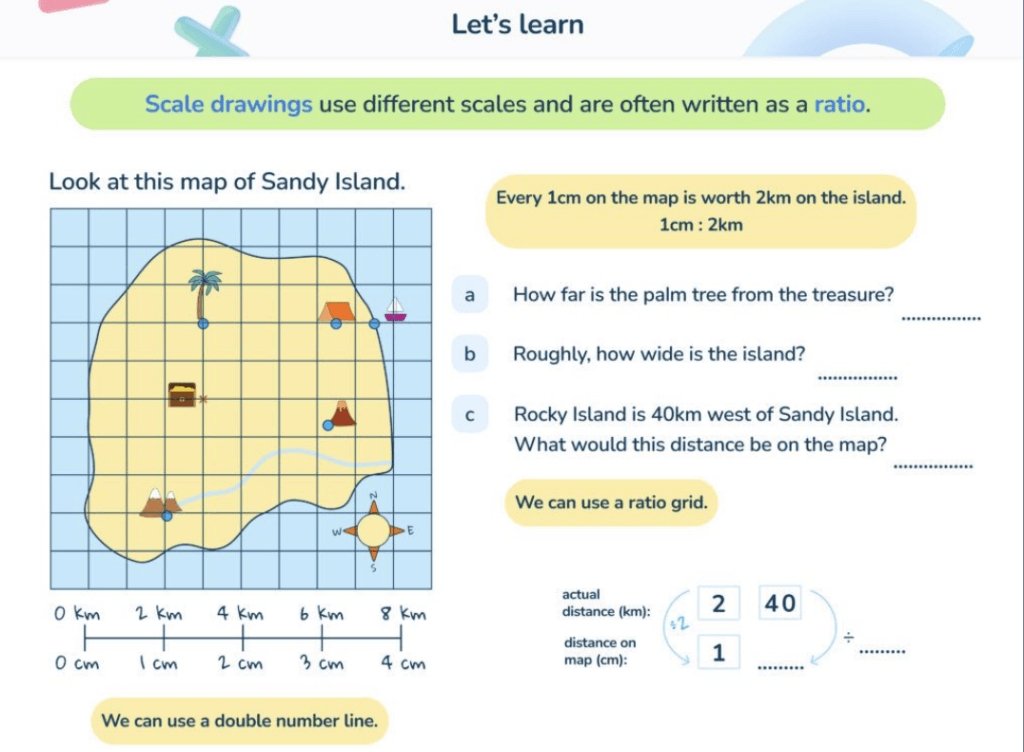
Sophie was trying to calculate the number of students in her school.
She found the ratio of boys to girls across the school was 3:2.
If there were 120 boys in the school…
- How many girls were there?
- How many students were there altogether?
Answer: a) 80 b) 200
a. 80 girls
This can be shown as a bar model.
120 ÷ 3 = 40
40 x 2 = 80
b. 200 students altogether
120 boys + 80 girls = 200
Students in the Eco Club in 6th Grade wanted to investigate how many worksheets were being printed each week in Math and English.
They found that there were 160 Math worksheets and 80 English worksheets being printed each week.
What is the ratio of Math to English worksheets? Write the ratio in simplest form.
Answer: 2:1
The ratio 160:80 can be simplified by dividing both sides by 80.
The 6th-grade rugby club has 30 members. The ratio of boys to girls is 4:1. How many boys and girls are in the club?
Answer: 24 boys and 6 girls
The ratio of 4:1 has 5 parts:
Boys: 4 x 6 = 24
Girls: 1 x 6 = 6
Yasmine has a necklace with purple and blue beads.
The ratio of purple:blue beads = 1:3
There are 24 beads on the necklace. How many purple and blue beads are there?
Answer: 6 purple beads and 18 blue beads
The ratio of 1:3 has 4 parts and 24 ÷ 4 = 6 beads per part.
Purple: 1 x 6 = 6
Blue: 3 x 6 = 18
Maisie drives past a field of sheep and cows.
She figures out that the ratio of sheep to cows is 3:1.
If there are 5 cows in the field, how many sheep are there?
Answer: 15 sheep
If there are 5 cows in the field, the 1 has been multiplied by 5.
We need to also multiply the 3 by 5, which is 15.

At a party, there is a choice of 2 flavors of jelly beans – orange and lemon.
The ratio of the jelly beans is 3:1 (orange: lemon).
What percent of the jelly beans are orange?
Answer: 75%
To find the percent, we need to write the ratio of orange jelly beans to total jelly beans. Since for every 3 orange jelly beans, there are 4 jelly beans in total (3 orange + 1 lemon = 4 total), the ratio is 3 to 4 or ¾.
To convert the ratio to a percent, the denominator needs to be 100.
Multiply both parts of the fraction by 25.
75/100 is equal to 75%.
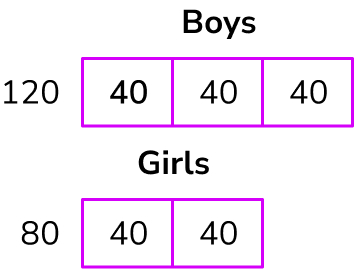
The school photocopier prints out 150 sheets in 3 minutes.
How many sheets can it print out in 15 minutes?
Answer: 750 sheets in 15 minutes
We need to multiply 3 by 5 to get 15 minutes. This means we also need to multiply 150 by 5 = 750.
Rowen wants to buy $80 worth of books. He will have to pay a 5% tax. How much will Rowen pay in total for the books?
Answer: $84
Since $8 is 10% of $8, then half will be 5%, which is $4.
$80 + $4 = $84
David has 2 grandchildren: Olivia (age 6) and Mia(age 3)
He decides to share $60 between the 2 children in a ratio of their ages.
How much does each child get?
Answer: Olivia gets $40, Mia gets $20
Ratio of 2:1 = 3 part and 60 ÷ 3 = $20 per part.
Olivia: 2 x 20 = $40
Mia: 1 x 20 = $20
A rectangle has the ratio of width to length 2:3. If the perimeter of the rectangle is 50cm, what’s the area?
Answer: Area: 150cm2
The ratio has 5 parts:
Divide 50 by 5 to work out 1 part = 10
The 2 widths must be 2 x 10 = 20
The 2 lengths must be 3 x 10 = 30
To work out the width of 1 side, divide the 20 by 2 = 10
To work out the length of 1 side, divide the 30 by 2 = 15
Width: 10cm and Length: 15cm
Area: 10 x 15 = 150cm 2
For a class field trip, 45% of students in Kinley’s class want to go to the zoo. The other students want to go to see a play. If 11 students want to go see a play, how many total students are in Kinley’s class?
Answer: 20 students
Since 5% is 1 student, then 45% is 9 students.
Adding the students that want to go to the zoo and the students that want to see a play, is the whole class, or 100% of the students.
11 + 9 = 20 students
A piece of ribbon is 45cm long.
It has been cut into 3 smaller pieces in a ratio of 4:5.
How long is each piece?
Answer: 20cm, 25cm
4:3:2 =9 parts: 45 ÷ 9 = 5cm per part.
4 x 5 = 20cm
3 x 5 = 25cm
Chloe is making a smoothie for her and her 3 friends.
She has the recipe for making a smoothie for 4 people: 240ml yogurt, 120 ml milk, 2 bananas, 180g strawberries and 1 tablespoon of sugar.
- How much yogurt would be needed to make a smoothie for 8 people.
- How many g of strawberries are needed to make the smoothie for 2 people?
- 480 ml yogurt
240ml x 2 = 480
- 90g strawberries
180 ÷ 2 = 90
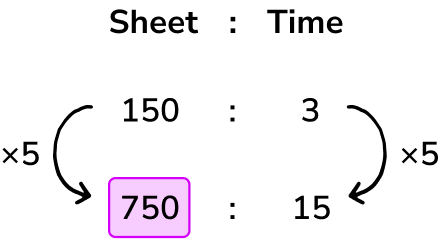
The ratio of cups of flour: cups of water in the recipe for making the dough for a pizza base is 7:4.
The pizza restaurant needs to make a large number of pizzas and is using 42 cups of flour. How much water will be needed?
Answer: 24 cups of water
Multiply 7 by 6 to get 42 cups of flour.
We, therefore, need to also multiply the 4 by 6 to calculate how many cups of water are needed.
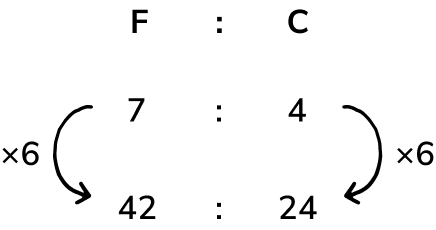
Muhammad shared $56 between him and his brother Hamza in a ratio of 3:5 (3 for Hamza and 5 for him).
How much did each get?
Answer: Muhammad got $35, his brother got $21
Ratio of 3:5 = 8 parts
56 ÷ 8 = $7 per part
3 x 7 =$ 21
5 x 7 = $35
Scott has read 40% of his book. If he has 168 pages left, how many total pages does the book have?
Answer: 280 pages
100% – 40% = 60%
The 168 pages represent the 60% that Scott has not read.
Since 60% is 168, dividing both by 6 shows that 10% is 28. And multiplying by 10 shows how many pages are in 100% of the book.
Ratio word problems for 7th grade
For every 250 tickets sold, the theater receives $687.50.
How much money did the theater charge for 1 ticket?
Answer: $2.75
The original ratio of tickets sold to dollars the theater made is 250 : 687.50.
To get liters to 1, divide both sides by 250.
A faucet drips ⅓ of a liter of water in ½ of an hour. How long does it take the faucet to drip 1 liter?
Answer: 1 and ½ hours
The original ratio of liters to hours ⅓ : ½.
To get liters to 1, multiply by sides by 3.
When liters is 1, hours is equal to 3/2 or 1 and ½.
The angles in a triangle are in the ratio of 3:4:5 for angles A, B and C.
Calculate the size of each angle.
Angle A: 45°
Angle B: 60°
Angle C: 75°
3:4:5 = 12 parts. 180 ÷ 12 = 15 (each part is worth 15°)
3 x 15 = 45
4 x 15 = 60
5 x 15 = 75
A drink is made by mixing pineapple and lemonade in the ratio of ⅔ of a cup to ⅘ of a cup. If Jayla has 1 cup of lemonade, how much pineapple should she add to keep the same drink ratio?
Answer: ⅚ of a cup
The original ratio of cups pineapple to lemonade is ⅔ :⅘.
To get cups of lemonade to 1, multiply by sides by 5/4.
When lemonade is 1 cup, pineapple is 10/12 or 5/6.
A $74 pair of shoes is on sale for 60% off. If Kalani buys two pairs of the shoes and pays the 7% tax on the total cost, how much money did Kalani spend in all?
Answer: $63.34
100% – 60% = 40%, so Kalani will pay 40% of the original price.
$74 0.4 = $29.60
The two pairs, before tax, cost: $29.60 + $29.60 = $59.20
Since 7% = 0.07, multiply $59.20 times 0.07 to calculate the tax.
$59.20 0.07 = $4.144 (round down to $4.14).
$59.20 + $4.14 = $63.34
*Note: You can also solve by multiplying $59.20 1.07 = $63.34
Jaxton bought a video game console for $650 two years ago. He just sold it for $475. What is the percent decrease, to the nearest percent, in the price of the game console from when Jaxton bought it to when he sold it?
Answer: 27%
$650 – $475 = $175
Divide the difference by the original price.
$175 $650 = 0.269…
To convert the decimal to a percent, multiply by 100.
0.269 100 = 26.9%, which rounds up to 27%.
Two companies are making an orange-colored paint.
Company A makes the orange paint by mixing red and yellow paint in a ratio of 5:7.
Company B makes the orange paint by mixing red and yellow paint in a ratio of 3:4.
Which company uses a higher proportion of red paint to make the orange?
Answer: Company B uses more red paint.
Company A: 5:7 = 5/12 is red
Company B: 3:4 = 3/7 is red
We can compare the fractions by giving them the same denominator, to find the equivalent fractions.
5/12 = 35/84
3/7 = 36/84
$8,142 is invested in a savings account with a 0.2% simple interest rate per month. What is the total interest earned after 4 years?
Answer: $781.63
Use the equation I=Prt:
t = 4 years x 12 = 48 months
$8,142 (0.002 x 48) = $781.632
$781.632 rounds to $781.63
More word problems
Looking for word problems on more topics? Take a look at our practice problems for Years 3-6 including money word problems , time word problems , addition word problems and subtraction word problems .
Do you have students who need extra support in math? Give your students more opportunities to consolidate learning and practice skills through personalized math tutoring with their own dedicated online math tutor. Each student receives differentiated instruction designed to close their individual learning gaps, and scaffolded learning ensures every student learns at the right pace. Lessons are aligned with your state’s standards and assessments, plus you’ll receive regular reports every step of the way. Personalized one-on-one math tutoring programs are available for: – 2nd grade tutoring – 3rd grade tutoring – 4th grade tutoring – 5th grade tutoring – 6th grade tutoring – 7th grade tutoring – 8th grade tutoring Why not learn more about how it works ?
The content in this article was originally written by former UK Deputy Headteacher and has since been revised and adapted for US schools by math curriculum specialist and former elementary math teacher Katie Keeton.
Related articles
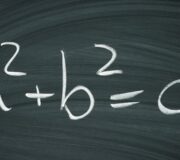
15 Pythagorean Theorem Practice Problems For 8th Grade

7 Questions You Should Ask When Reviewing Your Current Or Future Math Curriculum

The 12 Divisibility Rules You Need To Know (With A New One You’ve Probably Never Heard Of)
Math Games for 6th Graders [FREE]
On the lookout to make your math lessons fun and interactive while building math skills? Try our 6 printable math games for 6th graders.
Playable in pairs, teams or a whole class, our accompanying instructions and printable resources make preparation a breeze!
Privacy Overview

- Parallelogram
- Quadrilateral
- Parallelepiped
- Tetrahedron
- Dodecahedron
- Fraction Calculator
- Mixed Fraction Calculator
- Greatest Common Factor Calulator
- Decimal to Fraction Calculator
- Whole Numbers
- Rational Numbers
- Place Value
- Irrational Numbers
- Natural Numbers
- Binary Operation
- Numerator and Denominator
- Order of Operations (PEMDAS)
- Scientific Notation
Last modified on August 3rd, 2023
Ratio Word Problems
Here, we will learn to do some practical word problems involving ratios.
Amelia and Mary share $40 in a ratio of 2:3. How much do they get separately?
There is a total reward of $40 given. Let Amelia get = 2x and Mary get = 3x Then, 2x + 3x = 40 Now, we solve for x => 5x = 40 => x = 8 Thus, Amelia gets = 2x = 2 × 8 = $16 Mary gets = 3x = 3 × 8 = $24
In a bag of blue and red marbles, the ratio of blue marbles to red marbles is 3:4. If the bag contains 120 green marbles, how many blue marbles are there?
Let the total number of blue marbles be x Thus, ${\dfrac{3}{4}=\dfrac{x}{120}}$ x = ${\dfrac{3\times 120}{4}}$ x = 90 So, there are 90 blue marbles in the bag.
Gregory weighs 75.7 kg. If he decreases his weight in the ratio of 5:4, find his reduced weight.
Let the decreased weight of Gregory be = x kg Thus, 5x = 75.7 x = \dfrac{75\cdot 7}{5} = 15.14 Thus his reduced weight is 4 × 15.14 = 60.56 kg
A recipe requires butter and sugar to be in the ratio of 2:3. If we require 8 cups of butter, find how many cups of sugar are required. Write the equivalent fraction.
Thus, for every 2 cups of butter, we use 3 cups of sugar Here we are using 8 cups of butter, or 4 times as much So you need to multiply the amount of sugar by 4 3 × 4 = 12 So, we need to use 12 cups of sugar Thus, the equivalent fraction is ${\dfrac{2}{3}=\dfrac{8}{12}}$
Jerry has 16 students in his class, of which 10 are girls. Write the ratio of girls to boys in his class. Reduce your answer to its simplest form.
Total number of students = 16 Number of girls = 10 Number of boys = 16 – 10 = 6 Thus the ratio of girls to boys is ${\dfrac{10}{6}=\dfrac{5}{3}}$
A bag containing chocolates is divided into a ratio of 5:7. If the larger part contains 84 chocolates, find the total number of chocolates in the bag.
Let the total number of chocolates be x
Then the two parts are:
${\dfrac{5x}{5+7}}$ and ${\dfrac{7x}{5+7}}$
${\dfrac{7x}{5+7}}$ = 84
=> ${\dfrac{7x}{12}}$ = 84
Thus, the total number of chocolates that were present in the bag was 144
Leave a comment Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
- Privacy Policy
- Trigonometry
Join Our Newsletter
© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Course: 6th grade > Unit 1
- Ratio tables
- Solving ratio problems with tables
- Equivalent ratios
- Equivalent ratios: recipe
Equivalent ratio word problems
- Understanding equivalent ratios
- Equivalent ratios in the real world
- Interpreting unequal ratios
- Understand equivalent ratios in the real world
- Number Charts
- Multiplication
- Long division
- Basic operations
- Telling time
- Place value
- Roman numerals
- Fractions & related
- Add, subtract, multiply, and divide fractions
- Mixed numbers vs. fractions
- Equivalent fractions
- Prime factorization & factors
- Fraction Calculator
- Decimals & Percent
- Add, subtract, multiply, and divide decimals
- Fractions to decimals
- Percents to decimals
- Percentage of a number
- Percent word problems
- Classify triangles
- Classify quadrilaterals
- Circle worksheets
- Area & perimeter of rectangles
- Area of triangles & polygons
- Coordinate grid, including moves & reflections
- Volume & surface area
- Pre-algebra
- Square Roots
- Order of operations
- Scientific notation
- Proportions
- Ratio word problems
- Write expressions
- Evaluate expressions
- Simplify expressions
- Linear equations
- Linear inequalities
- Graphing & slope
- Equation calculator
- Equation editor
- Elementary Math Games
- Addition and subtraction
- Math facts practice
- The four operations
- Factoring and number theory
- Geometry topics
- Middle/High School
- Statistics & Graphs
- Probability
- Trigonometry
- Logic and proof
- For all levels
- Favorite math puzzles
- Favorite challenging puzzles
- Math in real world
- Problem solving & projects
- For gifted children
- Math history
- Math games and fun websites
- Interactive math tutorials
- Math help & online tutoring
- Assessment, review & test prep
- Online math curricula
| → → Ratios Find here an unlimited supply of worksheets with simple word problems involving ratios, meant for 6th-8th grade math. In , the problems ask for a specific ratio (such as, " "). In , the problems are the same but the ratios are supposed to be simplified. contains varied word problems, similar to these: Options include choosing the number of problems, the amount of workspace, font size, a border around each problem, and more. The worksheets can be generated as PDF or html files. Each worksheet is randomly generated and thus unique. The and is placed on the second page of the file. You can generate the worksheets — both are easy to print. To get the PDF worksheet, simply push the button titled " " or " ". To get the worksheet in html format, push the button " " or " ". This has the advantage that you can save the worksheet directly from your browser (choose File → Save) and then in Word or other word processing program. Sometimes the generated worksheet is not exactly what you want. Just try again! To get a different worksheet using the same options:
Use the generator to make customized ratio worksheets. Experiment with the options to see what their effect is.
 Primary Grade Challenge Math by Edward ZaccaroA good book on problem solving with very varied word problems and strategies on how to solve problems. Includes chapters on: Sequences, Problem-solving, Money, Percents, Algebraic Thinking, Negative Numbers, Logic, Ratios, Probability, Measurements, Fractions, Division. Each chapter’s questions are broken down into four levels: easy, somewhat challenging, challenging, and very challenging.
We will learn how to divide a quantity in a given ratio and its application in the word problems on ratio. 1. John weights 65.7 kg. If he reduces his weight in the ratio 5 : 4, find his reduced weight. Let the previous weight be 5x. x = \(\frac{65.7}{5}\) Therefore, the reduce weight = 4 × 13.14 = 52.56 kg. 2. Robin leaves $ 1245500 behind. According to his wish, the money is to be divided between his son and daughter in the ratio 3 : 2. Find the sum received by his son. We know if a quantity x is divided in the ratio a : b then the two parts are \(\frac{ax}{a + b}\) and \(\frac{bx}{a + b}\). Therefore, the sum received by his son = \(\frac{3}{3 + 2}\) × $ 1245500 = \(\frac{3}{5}\) × $ 1245500 = 3 × $ 249100 = $ 747300 3. Two numbers are in the ratio 3 : 2. If 2 is added to the first and 6 is added to the second number, they are in the ratio 4 : 5. Find the numbers. Let the numbers be 3x and 2x. According to the problem, \(\frac{3x + 2}{2x + 6}\) = \(\frac{4}{5}\) ⟹ 5(3x + 2) = 4 ⟹ 15x + 10 = 8x + 24 ⟹ 15x – 8x = 24 - 10 ⟹ x = \(\frac{14}{7}\) Therefore, the original numbers are: 3x = 3 × 2 = 6 and 2x = 2 × 2 = 4. Thus, the numbers are 6 and 4. 4. If a quantity is divided in the ratio 5 : 7, the larger part is 84. Find the quantity. Let the quantity be x. Then the two parts will be \(\frac{5x}{5 + 7}\) and \(\frac{7x}{5 + 7}\). Hence, the larger part is 84, we get \(\frac{7x}{5 + 7}\) = 84 ⟹ \(\frac{7x}{12}\) = 84 ⟹ 7x = 84 × 12 ⟹ 7x = 1008 ⟹ x = \(\frac{1008}{7}\) Therefore, the quantity is 144. ● Ratio and proportion
From Word Problems on Ratio to HOME PAGE Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need. New! Comments
Recent Articles6th grade math practice | table of contents | worksheets | videos math. Jul 08, 24 01:38 AM 5th Grade Math Problems | 5th Grade Math | Fifth Grade Math ProblemsJul 08, 24 12:55 AM Regular and Irregular Polygons | Definitions |Examples|Questions & AnsJul 07, 24 02:57 PM Different Types of Polygons | Triangle, Quadrilateral|Pentagon|HexagonJul 07, 24 10:28 AM  Quadrilateral Worksheet |Different Types of Questions in QuadrilateralJul 06, 24 04:24 PM  © and ™ math-only-math.com. All Rights Reserved. 2010 - 2024. Become a math whiz with AI Tutoring, Practice Questions & more. Word Problems: RatiosWhen we solve word problems, we often encounter ratios. Whether we're aware of it or not, our universe contains many ratios -- including the so-called " golden ratio " that is so common in nature. When we understand how ratios work, it's easy to solve all kinds of real-world problems . Let's get started: What is a ratio?A ratio is a comparison of two different values with the same units. We write these with colons. Here are a few examples: 5:1, 12:30, 1:2 The colon simply means "to," so "5:1" means a "five to one" ratio. Using our knowledge of ratios to solve word problemsLet's use our knowledge of ratios to tackle a few word problems: Let's say we have 12 sunfish and 30 rainbow shiners in our backyard pond. What is the ratio of sunfish to rainbow shiners in its simplest form? We can write the ratio 12:30 as the fraction 12 30 . Next, we can reduce this fraction to 2/5. Finally, we rewrite it as the ratio 2:5. We also know that the reverse is true, as the ratio of rainbow shiners to sunfish is 5:2. Now let's say we have a classroom of 32 students with 20 girls. What is the ratio of boys to girls? We know that the total is 32 -- but we can't make the mistake of giving 20/32 as our answer. This gives us the ratio of girls to the total number of students -- but it doesn't give us the ratio of girls to boys. To find the correct answer, we need the total number of boys. 30 - 18 = 12 boys Therefore, the ratio of girls to boys is 20:12 or 5:3 in simplified terms. Now let's say we're baking a cake using a recipe that calls for a butter-to-sugar ratio of 2:3. If we use 6 cups of butter, how many cups of sugar should we use? We know that we're using three times as much butter as the original recipe (since 6 is three times 2), so all we need to do is multiply the original sugar amount by three as well. 3 × 3 = 9 cups of sugar. So, if we use 6 cups of butter, we should use 9 cups of sugar to maintain the 2:3 butter-to-sugar ratio. Topics related to the Word Problems: RatiosEquivalent Ratios Word Problems Golden Ratio Flashcards covering the Word Problems: RatiosAlgebra 1 Flashcards College Algebra Flashcards Practice tests covering the Word Problems: RatiosAlgebra 1 Diagnostic Tests College Algebra Diagnostic Tests Help your student reach for their math goalsTutoring helps students reach for their top math goals, whether that involves new challenges outside of the normal curriculum or catching up with their peers. Our Educational Directors will create a tutoring plan for your student that matches up with their goals and their busy schedule, so contact Varsity Tutors today to get started.
Ratio Word Problems Calculator  How does the Ratio Word Problems Calculator work?What 3 formulas are used for the ratio word problems calculator, what 3 concepts are covered in the ratio word problems calculator, example calculations for the ratio word problems calculator.
 An Automated Online Math Tutor serving 8.1 million parents and students in 235 countries and territories.  Our Services
Top Categories
  In order to continue enjoying our site, we ask that you confirm your identity as a human. Thank you very much for your cooperation. HOW TO SOLVE RATIO WORD PROBLEMSIn this section, you will learn how word problems on ratio can be solved. Let us look at the stuff which are required to solve word problems on ratio. For example, If two persons A & B are earning $400 and $ 500 respectively per week, the ratio of their earnings is A : B = 400 : 500 When we simplify, we get A : B = 4 : 5 From the ratio 4:5, if we want to get the earning of A and B, we have to multiply the terms of the ratio 4 & 5 by 100. From the above point, it is very clear that if we want to get original quantity from the ratio, we have to multiply both the terms of the ratio by the same number. In the above problem, we know that we have to multiply by 100. In case, we do not know what number to be multiplied, we have to multiply by "x" or any alphabet. For example, the ages of two persons are in the ratio Age of the 1st person = 5x Age of the 2nd person = 6x (The value of 'x' to be found) If a quantity increases or decreases in the ratio a : b, then new quantity is = 'b' of the original quantity divided by 'a' new quantity = (b x original quantity) / a Increment Ratio : In a ratio, if the second term is greater than the first term, it is called increment ratio. Examples: 7 : 8 , 4 : 5, 1 : 5. Decrement Ratio : In a ratio, if the second term is smaller than the first term, it is called decrement ratio. Examples : 8 : 7, 4 : 3, 9 : 7. How to find increment ratio : A quantity called 'A' has been increased to '3A'. Now, to find the ratio in which it has been increased, just take the coefficient of A in the changed quantity '3A'. It is '3'. Now we have to write this '3' as a fraction. That is 3/1. From the fraction '3/1', we have to form a increment ratio. Because, the original quantity has been increased. Therefore, the increment ratio from '3/1' is 1 : 3. How to find decrement ratio : A quantity called 'A' has been decreased to '0.25A'. Now, to find the ratio in which it has been decreased, just take the coefficient of A in the changed quantity '0.25A'. It is '0.25'. Now we have to write this '0.25' as a fraction. That is '1/4'. From the fraction '1/4', we have to form a decrement ratio. Because, the original quantity has been decreased. Therefore, the decrement ratio from '1/4' is Let us see how the above explained stuff help us to solve the ratio word problem given below. Find in what ratio, will the total wages of the workers of a factory be increased or decreased if there be a reduction in the number of workers in the ratio 15:11 and an increment in their wages in the ratio 22:25. Let us understand the given information. There are two information given in the question. 1. In a factory, there is a reduction in the number of workers in the ratio 15:11. 2. There is an increment in their wages in the ratio 22:25. Target of the question : In what ratio, will the total wages of the factory be increased or decreased ? Let 'x' be the original number of workers Let 'y' be the wages per worker. Total wages = (No. of workers) x (wages per worker) Before the given two changes, Total wages = xy or 1xy After reduction in the number of workers in the ratio Number of workers in the factory is = 11x / 15 (see stuff 2) After increment in wages in the ratio Wages per worker is = 25y / 22 (see stuff 2) After the two changes, Total wages = (11x/15) x (25y/22) Total wages = (5/6)xy = (0.833)xy Total wages = 1xy ----(1) After the given two changes, Total wages = (0.83)xy ----(2) Comparing (1) and (2), it is very clear that total wages has been decreased when the two changes are applied. That is, total wages has been decreased from (1xy) to (0.83)xy Now, to find the ratio in which it has been decreased, just take the coefficient of 'xy' in total wages after the two changes applied. It is '0.83'. Now we have to write this '0.83' as a fraction. That is '5/6'. From the fraction '5/6', we have to form a decrement ratio. That is '5 : 6' (See stuff 4). Therefore, the total wages of the factory will be decreased in the ratio Kindly mail your feedback to [email protected] We always appreciate your feedback. © All rights reserved. onlinemath4all.com
Recent ArticlesBest way to learn mathematics. Jul 08, 24 07:39 AM Pre Calculus Problems and Solutions (Part -1)Jul 08, 24 07:35 AM  Pre Calculus Problems and Solutions (Part - 2)Jul 08, 24 07:28 AM Solving Word Problems with Ratios Hey guys! Welcome to this video tutorial on word problems involving ratios . Ratios are what we use to compare certain number values. People everywhere use ratios. We use, or at least we should, use ratios when we cook. For example, if I were to make macaroni and cheese for a group of 6 people and I knew that a \(\frac{1}{2}\) cup of macaroni would feed one person, then I could multiply 6 times \(\frac{1}{2}\) to get 3. Well, 3 to 6 is my ratio, and this ratio tells me that for every 3 cups of macaroni that I have, I can serve 6 people. But hang on. What if I told you that 1 cup of macaroni to every 2 persons is the same ratio as 3:6? Well, it’s the same ratio. 3:6 can be reduced to 1:2 because both 3 and 6 are divisible by 3, which is how we get \(\frac{1}{2}\). So, even though these two ratios look different, they are actually the same. Let’s take a look at a few word problems, and practice working through them. Example Problem 1There are 7 kids in a classroom with green shirts, 8 with red shirts, and 10 with yellow shirts. What is the ratio of people with red and yellow shirts? 7:10 8:7 8:10 4:5 Alright, so let’s look at our problem, and see what it is asking us to find, and write out the information that we have been given. So, there are 7 kids with green shirts; so, let’s write that down. We have Green: 7. We have 8 kids with red shirts, so that is Red: 8, and we have 10 kids with yellow shirts, Yellow: 10.  So now let’s look at each of our options and eliminate. It can’t be 7:10, we don’t care about the green shirts. It can’t be 8:7, because again we don’t care about the green shirts. Option C is correct; that is the exact number ratio we found. Now, look closely at D here. Is 4:5 not the same thing as 8:10? 8 and 10 are both divisible by 2, and when we reduce them both down we get 4:5, so D is also correct! Great, now let’s look at another word problem. Example Problem 2A vegetable tray contains 12 baby carrots, 27 cherry tomatoes, 18 florets of broccoli, and 45 slices of red bell peppers. For every 2 baby carrots, there are 3_____. Alright, let’s start off the same way that we did our last problem; read through the problem, write down what we know, and find out what is being asked. So, this vegetable tray contains 12 baby carrots. It contains 27 cherry tomatoes. We have 18 broccoli florets and 45 slices of red bell peppers.  When we look at all of our information written down, we can see that we have 18 broccoli florets; so there is our answer. For every 2 baby carrots, there are 3 broccoli florets. Another way to check and verify that these two ratios are equal is by setting them up in fraction form and cross multiplying. \(\frac{2}{3}=\frac{12}{18}\) When we cross multiply, we get \(36=36\). You can practice finding ratios anywhere you go, like finding the ratio of boys to girls in your class. I hope that this video helped you to understand how to solve word problems with ratios. See you guys next time! Frequently Asked QuestionsHow do you figure out ratios. A ratio is simply a comparison between two amounts. When figuring out ratios, it is important to consider what two values are being compared. This can be expressed in fraction form, in word form, or simply by using a colon. When writing a ratio that is comparing a “part” to the “whole”, list the “part” first, and the “whole” second. For example, if you eat \(3\) slices of pizza out of \(10\) slices total, you have eaten \(3\) out of \(10\) slices. This can be expressed as \(\frac{3}{10}\) or \(3\):\(10\), where the part is listed first, and the whole is listed second. Ratios can also be “part” to “part” comparisons. For example, if there are \(7\) boys in a class, and \(9\) girls in a class, the ratio of boys to girls is \(7\):\(9\). Make sure to match the order of the ratio to the order presented in the scenario. What are basic ratios?Ratios are used to directly compare two amounts. Basic ratios are used in many real-world situations, which makes it a valuable skill to master. Basic ratios can be expressed as fractions, words, or by using a colon. For example, \(\frac{4}{5}\), “four to five”, and \(4\):\(5\), all represent the same ratio. What are the 3 ways to write a ratio?A ratio is the comparison between two quantities. There is more than one way to write a ratio. For example, ratios can be written using a fraction bar, using a colon, or using words. \(\frac{5}{8}\) \(5\):\(8\) \(\text{five to eight}\) What are equivalent ratios?Ratios that have the same value are considered equivalent ratios . For example, if you slice a cake into \(10\) pieces, and you eat \(2\) pieces, you have eaten “\(2\) out of \(10\)” pieces, or \(2\):\(10\). If you had sliced the cake into \(20\) pieces, and eaten \(4\) pieces, you would have eaten the same amount of cake. Eating “4 out of 20” pieces is the same amount as eating “2 out of 10” pieces. Equivalent ratios occur when you multiply or divide both quantities of the ratio by the same amount. \(\frac{50}{100}\) is equivalent to \(\frac{5}{10}\) because when you divide both quantities of the ratio by \(10\), the result is \(\frac{5}{10}\). How do you find an equivalent ratio?Equivalent ratios can be thought of as equivalent fractions. Two ratios are equivalent if they represent the same amount. For example \(\frac{1}{2}\) and \(\frac{5}{10}\) are equivalent because they represent the same amount. Equivalent ratios are found by multiplying or dividing the numerator and denominator by the same amount. For example, \(3\):\(4\) and \(15\):\(20\) are equivalent ratios because both values in \(3\):\(4\) can be multiplied by \(5\) in order to create the ratio \(15\):\(20\). How do you solve ratio word problems?Ratios have many real-world applications. Word problems that involve ratios will usually require you to find an unknown value by finding an equivalent ratio. For example, if you made \($170\) washing \(10\) cars, how much money did you make per car? The ratio of dollars earned compared to cars washed is \(\frac{170}{10}\). We can divide both of these values by \(10\) in order to solve for the dollars earned for washing \(1\) car. \(\frac{170\div10}{10\div10}=\frac{17}{1}\). This means that \($17\) was earned per car. Many word problems involving ratios require you to create equivalent ratios. Remember, as long as you multiply or divide both values of a ratio by the same amount, you have not changed the ratio. How do you write a ratio in words?Ratios are used to compare two quantities. There are generally two ways to write a ratio in word form. When a ratio is considered a “part-out-of-whole” ratio, the phrase “out of” can be used. For example, if there is a pizza with \(8\) slices, and you eat \(2\) of those slices, you have eaten “\(2\) out of \(8\)” slices. However, some ratios are considered “part-to-part” ratios. For example, when comparing \(3\) green marbles to \(8\) red marbles, the phrase “\(3\) to \(8\)” can be used. How do you explain ratios and proportions?Ratios describe the relationship between two amounts. Ratios can be described as part-to-part or part-to-whole. For example, in a new litter of puppies, \(4\) of the pups are female and \(3\) of the pups are male. The part-to-part ratio \(4\):\(3\) would be used to compare female to male pups. When comparing female pups to the whole liter, the part-to-whole ratio \(4\):\(7\) would be used. Similarly, the ratio of male pups to total pups would be \(3\):\(7\). If two ratios are equivalent, they are said to be proportional. For example, if \(50\) meters of rope weighs \(5\) kilograms, and \(150\) meters of rope weighs \(15\) kilograms, the two amounts are proportional. \(50\):\(5\) is equivalent to \(150\):\(15\) because both values of the first ratio are multiplied by \(3\) in order to create the second ratio. What is a ratio, short answer?A ratio is a comparison between two amounts. Ratios can be written using a fraction bar \((\frac{3}{4})\), using a colon (\(3\):\(4\)), or using words (“three to four”). Ratios can be “part-to-part” or “part-to-whole”. For example, \(5\) green marbles and \(7\) red marbles would be a “part-to-part” ratio (\(5\):\(7\)). Solving \(95\) problems correctly out of \(100\) on a math test would be a “part-to-whole” ratio (\(95\):\(100\)). Ratio Word ProblemsCross multiply in order to determine which pair of ratios are equivalent. 3:5 and 4:9 6:7 and 7:8 7:8 and 35:40 12:25 and 14:17 The correct answer is 7:8 and 35:40. We can use cross multiplication to determine if two ratios are equivalent. Let’s look at the ratios for Choice C, and let’s set these up as fractions: \(\frac{7}{8}\) and \(\frac{35}{40}\) Now, cross multiply by finding the product of \(8×35\) and \(7×40\). In both cases our product is 280, so we know that the original ratios are equivalent. Which ratio is equivalent to \(\frac{36}{45}\)? The correct answer is 4:5. We can simplify ratios with the same strategy that we use to simplify fractions. In the ratio \(\frac{36}{45}\) we can divide the numerator and denominator by 9. \(\frac{36}{45}\) now becomes \(\frac{4}{5}\) or 4:5. James has a bag full of red, blue, and yellow candy. There are 10 red candies, 9 blue candies, and 11 yellow candies. What is the ratio of blue candies to total candies in the bag? Simplify the ratio if possible. The correct answer is 3:10. The total number of blue candies is 9, and the total number of candies in the bag is 30. If we set this ratio up as a fraction, we have \(\frac{9}{30}\). This fraction can be simplified if we divide the numerator and denominator by 3. Our final answer is \(\frac{3}{10}\) or 3:10. Alex is counting the coins in his pocket, and finds that he has 14 quarters, 7 nickels, and 4 dimes. What is the ratio of quarters to nickels? Simplify if possible. The correct answer is 2:1. We can compare the number of quarters to the number of nickels by setting up a ratio. There are 14 quarters and 7 nickels, so our ratio would be 14:7. Choice B says 14:7, but we should simplify when possible. 14:7 simplifies to 2:1. In Mr. Jenkin’s 4th grade class there are 14 boys and 17 girls. What is the ratio of boys to girls? Simplify if possible. The correct answer is 14:17. We can express this comparison of boys to girls as a ratio. 14 boys and 17 girls can be described as the ratio 14:17, or the fraction \(\frac{14}{17}\). 14 and 17 do not have any factors in common, so 14:17 is in simplest form. Return to Basic Arithmetic Videos by Mometrix Test Preparation | Last Updated: June 20, 2024 Ratio Word Problems - Two Terms RatioIn these lessons, we will learn how to solve ratio word problems involving 2-term ratios. Related Pages More Ratio Problems Math Word Problems Algebra Word Problems Math Worksheets Ratio problems are word problems that use ratios to relate the different items in the question. The main things to be aware about for ratio problems area:
Ratio problems: Two-term RatiosExample 1: In a bag of red and green sweets, the ratio of red sweets to green sweets is 3:4. If the bag contains 120 green sweets, how many red sweets are there? Solution: Step 1: Assign variables: Let x = red sweets Write the items in the ratio as a fraction. Step 2: Solve the equation Cross Multiply 3 × 120 = 4 × x 360 = 4 x Isolate variable x Answer: There are 90 red sweets. Example 2: John has 30 marbles, 18 of which are red and 12 of which are blue. Jane has 20 marbles, all of them either red or blue. If the ratio of the red marbles to the blue marbles is the same for both John and Jane, then John has how many more blue marbles than Jane? Solution: Step 1: Sentence: Jane has 20 marbles, all of them either red or blue. Assign variables: Let x = blue marbles for Jane 20 – x = red marbles for Jane We get the ratio from John John has 30 marbles, 18 of which are red and 12 of which are blue. We use the same ratio for Jane. 3 × x = 2 × (20 – x ) 3 x = 40 – 2 x John has 12 blue marbles. So, he has 12 – 8 = 4 more blue marbles than Jane. Answer: John has 4 more blue marbles than Jane. Ratios and solving ratio word problems Examples:
How to use proportions to solve ratio word problems? Examples:
 We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
The Supreme Court says cities can punish people for sleeping in public places Jennifer Ludden U.S. Supreme Court says cities can punish people for sleeping in public places A homeless person walks near an elementary school in Grants Pass, Ore., on March 23. The rural city became the unlikely face of the nation's homelessness crisis when it asked the U.S. Supreme Court to uphold its anti-camping laws. Jenny Kane/AP hide caption In its biggest decision on homelessness in decades, the U.S. Supreme Court today ruled that cities can ban people from sleeping and camping in public places. The justices, in a 6-3 decision along ideological lines, overturned lower court rulings that deemed it cruel and unusual under the Eighth Amendment to punish people for sleeping outside if they had nowhere else to go. Writing for the majority, Justice Gorsuch said, “Homelessness is complex. Its causes are many.” But he said federal judges do not have any “special competence” to decide how cities should deal with this. “The Constitution’s Eighth Amendment serves many important functions, but it does not authorize federal judges to wrest those rights and responsibilities from the American people and in their place dictate this Nation’s homelessness policy,” he wrote. In a dissent, Justice Sotomayor said the decision focused only on the needs of cities but not the most vulnerable. She said sleep is a biological necessity, but this decision leaves a homeless person with “an impossible choice — either stay awake or be arrested.” The court's decision is a win not only for the small Oregon city of Grants Pass, which brought the case, but also for dozens of Western localities that had urged the high court to grant them more enforcement powers as they grapple with record high rates of homelessness. They said the lower court rulings had tied their hands in trying to keep public spaces open and safe for everyone.  Supreme Court appears to side with an Oregon city's crackdown on homelessnessBut advocates for the unhoused say the decision won’t solve the bigger problem, and could make life much harder for the quarter of a million people living on streets, in parks and in their cars. “Where do people experiencing homelessness go if every community decides to punish them for their homelessness?” says Diane Yentel, president of the National Low Income Housing Coalition. Today’s ruling only changes current law in the 9th Circuit Court of Appeals, which includes California and eight other Western states where the bulk of America’s unhoused population lives. But it will also determine whether similar policies elsewhere are permissible; and it will almost certainly influence homelessness policy in cities around the country. Cities complained they were hamstrung in managing a public safety crisisGrants Pass and other cities argued that lower court rulings fueled the spread of homeless encampments, endangering public health and safety. Those decisions did allow cities to restrict when and where people could sleep and even to shut down encampments – but they said cities first had to offer people adequate shelter. That’s a challenge in many places that don’t have nearly enough shelter beds. In briefs filed by local officials, cities and town also expressed frustration that many unhoused people reject shelter when it is available; they may not want to go if a facility bans pets, for example, or prohibits drugs and alcohol. Critics also said lower court rulings were ambiguous, making them unworkable in practice. Localities have faced dozens of lawsuits over the details of what’s allowed. And they argued that homelessness is a complex problem that requires balancing competing interests, something local officials are better equipped to do than the courts. "We are trying to show there's respect for the public areas that we all need to have," Seattle City Attorney Ann Davison told NPR earlier this year. She wrote a legal brief on behalf of more than a dozen other cities. "We care for people, and we're engaging and being involved in the long-term solution for them." The decision will not solve the larger problem of rising homelessnessAttorneys for homeless people in Grants Pass argued that the city’s regulations were so sweeping, they effectively made it illegal for someone without a home to exist. To discourage sleeping in public spaces, the city banned the use of stoves and sleeping bags, pillows or other bedding. But Grants Pass has no public shelter, only a Christian mission that imposes various restrictions and requires people to attend religious service. "It's sort of the bare minimum in what a just society should expect, is that you're not going to punish someone for something they have no ability to control," said Ed Johnson of the Oregon Law Center, which represents those who sued the city. He also said saddling people with fines and a criminal record makes it even harder for them to eventually get into housing. Johnson and other advocates say today’s decision won’t change the core problem behind rising homelessness: a severe housing shortage, and rents that have become unaffordable for a record half of all tenants. The only real solution, they say, is to create lots more housing people can afford – and that will take years.
How much did debate hurt Biden's re-election bid? New poll offers insight.Trump's new, narrow advantage signals a close contest, not a decisive lead. but other exclusive poll findings raise red flags for the president..  Republican Donald Trump has edged ahead of Democrat Joe Biden , 41% to 38%, in the aftermath of the candidates' rancorous debate last week , according to an exclusive USA TODAY/Suffolk University Poll. That narrow advantage has opened since the previous survey in May showed the two contenders tied, 37% to 37% . The findings still signal a close contest, not a decisive lead. The difference in support and the shifts since the spring are within the polls' margins of error of plus or minus 3.1 percentage points. The new survey of 1,000 registered voters was taken Friday through Sunday by landline and cell phone. There was little change in the standing of third-party candidates, with independent Robert F. Kennedy Jr., at 8% and three others at about 1% each. But other findings in the poll raised red flags for President Biden, whose campaign has been roiled by his faltering performance in the CNN debate last Thursday. In the survey, 41% of Democrats said they wanted Biden replaced at the top of the ticket. "I think people are more focused on age, rather than with what the reality of our everyday could be under the two different administrations," said Shalia Murray, 57, a Democrat from Round Rock, Texas, who works in law enforcement and was called in the poll. She enthusiastically supports Biden but worries about voter apathy and a focus on "very surface issues." "I don't believe a lot of people believe that we could actually go backwards in our rights and in our freedoms" in a Trump administration, she said. Trump now leads as the second choice of voters: 25% of those surveyed said Trump was their second choice, compared with 17% for Biden. Thirty-three percent said their second choice was one of four third-party contenders: independent Cornel West, Green Party candidate Jill Stein, Libertarian candidate Chase Oliver and RFK Jr. "It is still a margin of error race right now, but the Biden campaign must be concerned about the defection of second-choice votes of third-party voters," David Paleologos, director of the Suffolk Political Research Center, said. Some Democratic strategists had calculated those voters would drift back to Biden as Election Day neared. "They now favor Trump instead of Biden," he said. "The Stein/West/RFK voters he may have been counting on in November have left him after Thursday's debate." The enthusiasm gap could affect turnoutTrump voters are also much more excited about their candidate than Biden voters are about theirs. That enthusiasm gap could be critical when it comes to convincing supporters to actually cast a ballot in the fall. "I like Trump," said Zach Anderson, 30, a maintenance technician and a Republican from South Chicago, Illinois. "The country was running just fine four or five years ago with him, and I can only see him doing a better job than he did last time because he has four years of experience." In contrast, Steve Sutton, a political independent from Seattle who works in IT, said he is for Biden in part simply because he is against Trump. In the debate, "Biden seems too old, and Trump can't tell the truth," he said. "So those are the two things coming out of it, and those are both, you know, right on the mark."
After years of sharpening political polarization, most partisans say their minds are firmly made up, including 87% of Biden voters and 89% of Trump voters. Just 10% of Biden supporters and 12% of Trump supporters say they might change their minds. However, most of those backing third-party candidates said their minds might change, from 56% of Kennedy's backers to 80% of those supporting Stein. Overall, 17% of those surveyed said they might change their minds. More details: Joe Biden's core Democratic support takes big hit after debate, exclusive poll shows For many, that would require a change in the nominees. In response to an open-ended question, 21% said "different candidates" and 16% said "a better candidate" would make them reconsider their choices. There was skepticism about the power of the Republican national convention in July and the Democratic national convention in August to persuade. Fourteen percent said the two conventions might change their minds, and 12% said the Democratic convention might. But a negligible 2% said the GOP convention might change their minds. When it comes to congressional elections, 47% said they would vote for the unnamed Republican candidate in their district; 45% for the Democratic one. That edge, while small, could be encouraging for GOP hopes of retaining their narrow majority in the House of Representatives. Trump supporters suspicious of the countTrump's unsubstantiated allegations that the 2020 election was stolen from him have reinforced significant doubts among his supporters about whether they can trust the vote count this year. In the poll, 44% of Trump supporters were "not confident" that the 2024 results would be accurately counted and reported, and another 45% said they were only "somewhat confident." In contrast, 83% of Biden supporters were "very confident" in a fair count. That said, Biden supporters were less certain they would prevail: 73% predicted a Biden victory, 12% a Trump win. Trump supporters were more bullish about November: 88% predicted Trump would win, just 4% Biden. My husband died by suicide. How would I tell our young children?The state trooper had delivered the news of Seth’s death. Soon, I was laser-focused on solving a single problem: How to tell the girls. It was 10 years ago — July 1, 2014 — that everything changed. A grim-faced state trooper pulled up to my house. I saw him from the living room window as he stepped out of the cruiser. He slammed the car door shut and took his time letting himself in through the wooden gate. He turned down the stone path. His slow, plodding footsteps gave him away. I flung open the front door and rushed down the steps toward him. Part of me knew before I asked. I remember the opposing compulsions tugging me in two at that moment: I want to know, I don’t want to know, like a child in a field, picking petals off a daisy. He loves me, he loves me not. I hesitated, just for a second, to speak. But the cop had a mission to complete. He was steady, stone-faced, with militaristic precision to his steps. All morning, I’d been desperate for news of Seth, my husband, an MIT professor and father of our daughters, then 8 and 11. Here, finally, was the messenger. So often, the truth is nuanced, multifaceted, subjective, shaded gray. But this fact striding toward my doorstep was that rare, eminent type of truth: particular and inescapable. “Is he dead?” I asked. The cop’s response began with a gesture of his head. I saw it start to move, slowly, up and then down. As it did, mine began to shift too, rotating to the right, to the left and back, almost like we were locked in a dance, except that his motions finally stopped, while mine grew steadily faster, overwhelming my entire body, shaking off every moment that came before. The cop nodded, “Yes.” I fell to my knees, weeping, howling the only thoughts I could summon into words: “The girls, the girls, Oh God, the girls,” like an old vinyl record stuck in a scratched groove. The trooper took my arm. The world collapsed into a sickening, hyper-real haze. I floated above my body briefly, saw myself below like a Sicilian widow in a Coppola movie. But I could not dissociate from the pain for my young daughters. Kneeling there, I felt I’d failed my key job as a mother, to protect them. As I tried to stand back up, my limbs, once solid, had now turned rubbery, unreliable. I leaned against the policeman as he led me back indoors, handing me over to a cousin who had arrived during my frantic morning search. As we entered my living room, the state trooper cleared his throat uncomfortably. He asked if my daughters’ names were Sophia and Julia. I nodded. He looked straight at me: “There’s a note.” It was left on the dashboard of Seth’s car, abandoned on the Tobin Bridge from which he jumped. I thought I’d vomit. “I don’t want it in here,” I said. “I can’t read it.” My cousin walked with the cop back to his car where she took the single sheet of paper. She quickly folded it away, promising to keep it safe. Then she returned, placed her arms around my shoulders and begged me to breathe. In that instant all of the previous roles I’d embodied — wife, journalist, daughter — dissolved. The clarity of my new vocation as a ferocious watchdog mother infused my entire nervous system. I felt myself lapse into a kind of madness. My reality seemed impossible to inhabit. How do I tell my children, “Daddy died.” And, worse, how he died. They would never recover. I sat on the couch, the last place I’d seen Seth that morning. My body was numb except for the dry matte of my tongue, thick and sour, like a bad piece of meat. Staring at the unfinished puzzle left on the floor, the one he’d worked on with the girls only hours earlier, I felt that language itself had betrayed me. Soothing words like “Marriage,” “Promise,” “Father” struck me now as poisonous, no longer bestowing the luxurious comforts that had tethered our lives. I had no backup to cling to, no map. Yet I was fully aware of a deadline looming. The state trooper had delivered the news of Seth’s death shortly before noon. Within about an hour, I’d snapped into a mental state that was laser-focused on solving a single problem: How to tell the girls. Now in my small office upstairs, I glanced at the old digital clock atop my wooden desk. It read 1:10 p.m. Day camp pickup was at three. How did a mother tell young children about their father’s death, I wondered. I desperately needed a script. As a journalist, there was one thing I understood well: how to track down an expert for guidance. I dialed a trusted work colleague and explained that I required fast help finding the right words for Sophia and Julia. “I’m on it,” she said. Ten minutes later, my colleague phoned back. I should stand by, she said. Then the phone rang again. Accustomed to speaking with strangers, I immediately blurted out my dilemma as soon as Dr. Paula Rauch, a psychiatrist from Massachusetts General Hospital, spoke her name. “My husband is dead. My kids don’t know. What do I say?” As I sat clutching my phone, Rauch calmly walked me through the language I might use to explain the unimaginable to my children. I should speak plainly , she said. I could tell them their daddy had an illness in his brain. We couldn’t see it, but just like cancer, it took over his body and made him die. There was nothing any of us could have done. It was nobody’s fault. Don’t lie, she advised, but don’t offer too many details. I nodded throughout, saying little, taking notes. Let them know they are safe and you’re not leaving, she said. Acknowledge their pain. Reassure them you will muddle through, things will get better. Hanging up, I exhaled for what felt like the first time all day. I always appreciated a solid plan. This prescription, in the form of her words, offered me a lifeline. When the time came, I drove the quarter mile from my house to the children’s camp and parked in the nearby lot. Thankfully, I wasn’t alone in the car. I knew it was best to speak to the kids on my own, but I was also becoming aware of a dynamic I’d largely avoided in parenting thus far: requiring help. Before this moment, I had considered myself one of those older, therefore wiser, super-moms who could effortlessly go it alone. Now, I knew I wouldn’t be able to drive the girls home by myself after telling them. So, there in the car with me was my mother, who’d broken the speed limit all the way from Cape Cod to Cambridge that morning when I called her with the news. I’d also asked Maria, the children’s longtime babysitter, to join me for support. They waited in the car as I stepped outside. I fixed my eyes on the girls as I walked hesitantly toward them. I felt the contrast between the burdensome weight of my knowledge and their easy, lighthearted ignorance. I pulled out my phone and snapped a photo of Julia, cross-legged on the ground, sitting in a circle of friends, giggling and clapping hands with the other children awaiting pickup. I wanted a record of what I believed would be her final carefree moment. In a robotic stupor, my body adopted the persona I’d rehearsed over the past hours. I waved. They approached me. I led them to a wobbly chrome table outside Anna’s Taqueria, their favorite burrito place. I pulled both girls in close and told them I had very bad news. “Girls, a terrible, terrible thing happened,” I said, holding their small hands. I paused. “Daddy died.” I couldn’t bear the silence that I expected would follow, so I began chattering to fill the space. “It was kind of an accident, but worse,” I said, grasping for phrasing that might offer some slight relief. “I don’t know all the details, there’s still a lot we don’t understand. But it’s true. And I am so, so sorry and I know it feels impossible now, but we will stay together and take care of each other and go on.” The disbelief on their faces was so stark that I felt I had to repeat myself. “He’s dead.” Sophia, who looks like Seth — with her tight, dark curls and deep set eyes — cried, “No!” and “How?” Julia stood up on her chair: “I’m not even double digits yet,” she wailed. When sundown finally arrived, someone, mercifully, brought me an Ativan. I tossed four extra pillows onto my bed. “We’re sleeping together,” I told the girls. It’s something we never repeated, despite my offers, because it triggered flashbacks of that day. While I held them, I replayed the nightmare morning in my head: the unanswered calls to Seth’s phone, the rising dread, the cop arriving, the note. Each memory, I believed, eroded any hope for an untroubled future. With my children’s hot breath against my neck, and the time nearing 3 a.m., I tried to blot out these thoughts. Soon, we would have to endure another day. There would be decisions for me to make. I tried to yield toward a woozy, drugged half-sleep, still checking, with each passing hour, that their small chests continued to rise and fall. Rachel Zimmerman is a journalist and writer based in Cambridge, Mass. who has previously written for The Washington Post and the Wall Street Journal. This is an excerpt from her book, “ Us, After: A Memoir of Love and Suicide ,” to be published June 30. Read more from Well+BeingWell+Being shares news and advice for living well every day. Sign up for our newsletter to get tips directly in your inbox. A mystery illness stole their kids’ personalities. These moms fought for answers. ‘Menopause brain’ is real. Here’s how women’s brains change in midlife. I’m an oncologist. Here’s what I advised my mom after her cancer diagnosis. How to pick a retirement home and thrive High levels of ultra-processed foods linked with early death , brain issues   | |||||||||||||||||||
COMMENTS
In this video I'll show you how to solve multiple types of Ratio Word Problems using 5 examples. We'll start simple and work up to solving the most complex p...
Ratio problem solving is a collection of ratio and proportion word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem. ...
Ratio Word Problems: relating different things using ratios and algebra, how to solve ratio word problems that have two-term ratios or three-term ratios, How to solve proportion word problems, questions and answers, with video lessons, examples and step-by-step solutions.
This video focuses on how to solve ratio word problems. In particular, I show students the trick of multiplying each term in the ratio by x to help set up an...
Ratios in 7th grade. Students in 7th grade continue to build on their knowledge of ratio from 6th grade. Calculate unit rates and solve problems for ratios comparing two fractions. Solve problems involving proportional relationships. Solve problems involving percentage change, including: percentage increase, decrease and original value problems ...
Playlists:========🍁HCF Trickshttps://www.youtube.com/watch?v=HfU8Jto7E6E🍁HCFhttps://www.youtube.com/watch?v=6c4ySF2Ykko🍁Decimalshttps://www.youtube.com/wa...
Discover how to solve ratio problems with a real-life example involving indoor and outdoor playtimes. Learn to use ratios to determine the number of indoor and outdoor playtimes in a class with a 2:3 ratio and 30 total playtimes. ... What you need to do in any word problem involving the ratios is exactly the same. Take the entire amount and ...
Express each ratio of two quantities by writing its numerical values as a fraction. Remember, that's one of the three ways to write a ratio. Find an equivalent ratio, and then set these fractions ...
Equivalent ratio word problems. Google Classroom. Microsoft Teams. About. Transcript. This video teaches solving ratio word problems, using examples like Yoda Soda for guests, fish ratios in a tank, ice cream sundae ingredients, and dog color ratios at a park. Mastering these techniques helps students tackle real-world math challenges. Questions.
Two-Term Ratio Word Problems More Ratio Word Problems Math Word Problems Singapore Math Lessons. Solving Ratio Problems Using A Tape Diagram. Things to Remember: Write your ratio as a fraction and label next to each part. Draw your boxes (connected or separated). Match the additional info. with the part of your ratio. Fill your boxes with the ...
Write the ratio of girls to boys in his class. Reduce your answer to its simplest form. Solution: Total number of students = 16. Number of girls = 10. Number of boys = 16 - 10 = 6. Thus the ratio of girls to boys is 10 6 = 5 3. A bag containing chocolates is divided into a ratio of 5:7. If the larger part contains 84 chocolates, find the ...
How to solve Ratio Word Problems with three terms? Example: A piece of string that is 63 inches long is cut into 3 parts such that the lengths of the parts of the string are in the ratio of 5 to 6 to 10. Find the lengths of the 3 parts. Show Video Lesson.
Equivalent ratio word problems. A fruit basket is filled with 8 bananas, 3 oranges, 5 apples, and 6 kiwis. Complete the ratio. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education ...
Ratio Worksheets. Columns: Rows: (These determine the number of problems) Level: Level 1: write a ratio. Level 2: write a ratio and simplify it. Numbers used (only for levels 1 & 2): Range from to with step. Level 3: word problems.
Therefore, the original numbers are: 3x = 3 × 2 = 6 and 2x = 2 × 2 = 4. Thus, the numbers are 6 and 4. 4. If a quantity is divided in the ratio 5 : 7, the larger part is 84. Find the quantity. Solution: Let the quantity be x. Then the two parts will be 5x 5+7 5 x 5 + 7 and 7x 5+7 7 x 5 + 7. Hence, the larger part is 84, we get.
What is a ratio? A ratio is a comparison of two different values with the same units. We write these with colons. Here are a few examples: 5:1, 12:30, 1:2 The colon simply means "to," so "5:1" means a "five to one" ratio. Using our knowledge of ratios to solve word problems. Let's use our knowledge of ratios to tackle a few word problems:
Solve. Crop Image ×. Crop. Enter Ratio Problem ... Solves a ratio word problem using a given ratio of 2 items in proportion to a whole number. This calculator has 1 input. What 3 formulas are used for the Ratio Word Problems Calculator? a:b ratio means a + b = c total options Expected Number of A = a * n/c
Solving Word Problems Involving Part to Whole Ratios. Step 1: Add the parts of the ratio to get the whole. Step 2: Identify the ratio between the whole and the part asked in the problem. Step 3 ...
Stuff 1: For example, If two persons A & B are earning $400 and $ 500 respectively per week, the ratio of their earnings is. A : B = 400 : 500. When we simplify, we get. A : B = 4 : 5. From the ratio 4:5, if we want to get the earning of A and B, we have to multiply the terms of the ratio 4 & 5 by 100.
http://www.mathtestace.comhttp://www.mathtestace.com/fraction-word-problems/Need help solving word problems with ratios and fractions? This video will walk y...
A. Ratios are used to compare two quantities. There are generally two ways to write a ratio in word form. When a ratio is considered a "part-out-of-whole" ratio, the phrase "out of" can be used. For example, if there is a pizza with 8 8 slices, and you eat 2 2 of those slices, you have eaten " 2 2 out of 8 8 " slices.
To delve deeper into these limitations, the research team tested GPT-3.5's ability to solve 728 coding problems from the LeetCode platform across five programming languages: C, C++, Java ...
The main things to be aware about for ratio problems area: Change the quantities to the same unit if necessary. Write the items in the ratio as a fraction. Make sure that you have the same items in the numerator and denominator. Ratio problems: Two-term Ratios. Example 1: In a bag of red and green sweets, the ratio of red sweets to green sweets ...
But advocates for the unhoused say the decision won't solve the bigger problem, and could make life much harder for the quarter of a million people living on streets, in parks and in their cars. ...
Remarkable story shows how we can solve America's problems. In Possum Trot, Texas, a single church changed the lives of dozens of children in foster care. Evan Feinberg. Opinion contributor.
Kahn: I don't think it's really a consensus, honestly, Erik, because I think it's just factually wrong.For any, frankly, even occasional reader of the New York Times to make an assessment of ...
As a result, the Bills could be looking toward the future in the 2025 NFL Draft. And in a recent mock draft from USA Today, the team selects a potential replacement for Miller. The site predicts ...
I solve two word problems that involve ratios, each time with the help of a bar model or diagram - Singapore Math style. The bar or block model is incredibly...
How much did debate hurt Biden's re-election bid? New poll offers insight. Trump's new, narrow advantage signals a close contest, not a decisive lead.
The cop's response began with a gesture of his head. I saw it start to move, slowly, up and then down. As it did, mine began to shift too, rotating to the right, to the left and back, almost ...