how to solve word problems rates

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 8: Rational Expressions

8.8 Rate Word Problems: Speed, Distance and Time

Distance, rate and time problems are a standard application of linear equations. When solving these problems, use the relationship rate (speed or velocity) times time equals distance .

[latex]r\cdot t=d[/latex]

For example, suppose a person were to travel 30 km/h for 4 h. To find the total distance, multiply rate times time or (30km/h)(4h) = 120 km.

The problems to be solved here will have a few more steps than described above. So to keep the information in the problem organized, use a table. An example of the basic structure of the table is below:

The third column, distance, will always be filled in by multiplying the rate and time columns together. If given a total distance of both persons or trips, put this information in the distance column. Now use this table to set up and solve the following examples.

Example 8.8.1

Joey and Natasha start from the same point and walk in opposite directions. Joey walks 2 km/h faster than Natasha. After 3 hours, they are 30 kilometres apart. How fast did each walk?

The distance travelled by both is 30 km. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrrrl} 3r&+&3(r&+&2)&=&30 \\ 3r&+&3r&+&6&=&30 \\ &&&-&6&&-6 \\ \hline &&&&\dfrac{6r}{6}&=&\dfrac{24}{6} \\ \\ &&&&r&=&4 \text{ km/h} \end{array}[/latex]

This means that Natasha walks at 4 km/h and Joey walks at 6 km/h.

Example 8.8.2

Nick and Chloe left their campsite by canoe and paddled downstream at an average speed of 12 km/h. They turned around and paddled back upstream at an average rate of 4 km/h. The total trip took 1 hour. After how much time did the campers turn around downstream?

The distance travelled downstream is the same distance that they travelled upstream. Therefore, the equation to be solved is:

[latex]\begin{array}{rrlll} 12(t)&=&4(1&-&t) \\ 12t&=&4&-&4t \\ +4t&&&+&4t \\ \hline \dfrac{16t}{16}&=&\dfrac{4}{16}&& \\ \\ t&=&0.25&& \end{array}[/latex]

This means the campers paddled downstream for 0.25 h and spent 0.75 h paddling back.

Example 8.8.3

Terry leaves his house riding a bike at 20 km/h. Sally leaves 6 h later on a scooter to catch up with him travelling at 80 km/h. How long will it take her to catch up with him?

The distance travelled by both is the same. Therefore, the equation to be solved is:

[latex]\begin{array}{rrrrr} 20(t)&=&80(t&-&6) \\ 20t&=&80t&-&480 \\ -80t&&-80t&& \\ \hline \dfrac{-60t}{-60}&=&\dfrac{-480}{-60}&& \\ \\ t&=&8&& \end{array}[/latex]

This means that Terry travels for 8 h and Sally only needs 2 h to catch up to him.

Example 8.8.4

On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took 2.5 h. For how long did the car travel 40 km/h?

[latex]\begin{array}{rrrrrrr} 55(t)&+&40(2.5&-&t)&=&130 \\ 55t&+&100&-&40t&=&130 \\ &-&100&&&&-100 \\ \hline &&&&\dfrac{15t}{15}&=&\dfrac{30}{15} \\ \\ &&&&t&=&2 \end{array}[/latex]

This means that the time spent travelling at 40 km/h was 0.5 h.

Distance, time and rate problems have a few variations that mix the unknowns between distance, rate and time. They generally involve solving a problem that uses the combined distance travelled to equal some distance or a problem in which the distances travelled by both parties is the same. These distance, rate and time problems will be revisited later on in this textbook where quadratic solutions are required to solve them.

For Questions 1 to 8, find the equations needed to solve the problems. Do not solve.

• A is 60 kilometres from B. An automobile at A starts for B at the rate of 20 km/h at the same time that an automobile at B starts for A at the rate of 25 km/h. How long will it be before the automobiles meet?
• Two automobiles are 276 kilometres apart and start to travel toward each other at the same time. They travel at rates differing by 5 km/h. If they meet after 6 h, find the rate of each.
• Two trains starting at the same station head in opposite directions. They travel at the rates of 25 and 40 km/h, respectively. If they start at the same time, how soon will they be 195 kilometres apart?
• Two bike messengers, Jerry and Susan, ride in opposite directions. If Jerry rides at the rate of 20 km/h, at what rate must Susan ride if they are 150 kilometres apart in 5 hours?
• A passenger and a freight train start toward each other at the same time from two points 300 kilometres apart. If the rate of the passenger train exceeds the rate of the freight train by 15 km/h, and they meet after 4 hours, what must the rate of each be?
• Two automobiles started travelling in opposite directions at the same time from the same point. Their rates were 25 and 35 km/h, respectively. After how many hours were they 180 kilometres apart?
• A man having ten hours at his disposal made an excursion by bike, riding out at the rate of 10 km/h and returning on foot at the rate of 3 km/h. Find the distance he rode.
• A man walks at the rate of 4 km/h. How far can he walk into the country and ride back on a trolley that travels at the rate of 20 km/h, if he must be back home 3 hours from the time he started?

Solve Questions 9 to 22.

• A boy rides away from home in an automobile at the rate of 28 km/h and walks back at the rate of 4 km/h. The round trip requires 2 hours. How far does he ride?
• A motorboat leaves a harbour and travels at an average speed of 15 km/h toward an island. The average speed on the return trip was 10 km/h. How far was the island from the harbour if the trip took a total of 5 hours?
• A family drove to a resort at an average speed of 30 km/h and later returned over the same road at an average speed of 50 km/h. Find the distance to the resort if the total driving time was 8 hours.
• As part of his flight training, a student pilot was required to fly to an airport and then return. The average speed to the airport was 90 km/h, and the average speed returning was 120 km/h. Find the distance between the two airports if the total flying time was 7 hours.
• Sam starts travelling at 4 km/h from a campsite 2 hours ahead of Sue, who travels 6 km/h in the same direction. How many hours will it take for Sue to catch up to Sam?
• A man travels 5 km/h. After travelling for 6 hours, another man starts at the same place as the first man did, following at the rate of 8 km/h. When will the second man overtake the first?
• A motorboat leaves a harbour and travels at an average speed of 8 km/h toward a small island. Two hours later, a cabin cruiser leaves the same harbour and travels at an average speed of 16 km/h toward the same island. How many hours after the cabin cruiser leaves will it be alongside the motorboat?
• A long distance runner started on a course, running at an average speed of 6 km/h. One hour later, a second runner began the same course at an average speed of 8 km/h. How long after the second runner started will they overtake the first runner?
• Two men are travelling in opposite directions at the rate of 20 and 30 km/h at the same time and from the same place. In how many hours will they be 300 kilometres apart?
• Two trains start at the same time from the same place and travel in opposite directions. If the rate of one is 6 km/h more than the rate of the other and they are 168 kilometres apart at the end of 4 hours, what is the rate of each?
• Two cyclists start from the same point and ride in opposite directions. One cyclist rides twice as fast as the other. In three hours, they are 72 kilometres apart. Find the rate of each cyclist.
• Two small planes start from the same point and fly in opposite directions. The first plane is flying 25 km/h slower than the second plane. In two hours, the planes are 430 kilometres apart. Find the rate of each plane.
• On a 130-kilometre trip, a car travelled at an average speed of 55 km/h and then reduced its speed to 40 km/h for the remainder of the trip. The trip took a total of 2.5 hours. For how long did the car travel at 40 km/h?
• Running at an average rate of 8 m/s, a sprinter ran to the end of a track and then jogged back to the starting point at an average of 3 m/s. The sprinter took 55 s to run to the end of the track and jog back. Find the length of the track.

Answer Key 8.8

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

"Work" Word Problems

Painting & Pipes Tubs & Man-Hours Unequal Times Etc.

"Work" problems usually involve situations such as two people working together to paint a house. You are usually told how long each person takes to paint a similarly-sized house, and you are asked how long it will take the two of them to paint the house when they work together.

Many of these problems are not terribly realistic — since when can two laser printers work together on printing one report? — but it's the technique that they want you to learn, not the applicability to "real life".

The method of solution for "work" problems is not obvious, so don't feel bad if you're totally lost at the moment. There is a "trick" to doing work problems: you have to think of the problem in terms of how much each person / machine / whatever does in a given unit of time . For instance:

Content Continues Below

MathHelp.com

Suppose one painter can paint the entire house in twelve hours, and the second painter takes eight hours to paint a similarly-sized house. How long would it take the two painters together to paint the house?

To find out how much they can do together per hour , I make the necessary assumption that their labors are additive (in other words, that they never get in each other's way in any manner), and I add together what they can do individually per hour . So, per hour, their labors are:

But the exercise didn't ask me how much they can do per hour; it asked me how long they'll take to finish one whole job, working togets. So now I'll pick the variable " t " to stand for how long they take (that is, the time they take) to do the job together. Then they can do:

This gives me an expression for their combined hourly rate. I already had a numerical expression for their combined hourly rate. So, setting these two expressions equal, I get:

I can solve by flipping the equation; I get:

An hour has sixty minutes, so 0.8 of an hour has forty-eight minutes. Then:

They can complete the job together in 4 hours and 48 minutes.

The important thing to understand about the above example is that the key was in converting how long each person took to complete the task into a rate.

hours to complete job:

first painter: 12

second painter: 8

together: t

Since the unit for completion was "hours", I converted each time to an hourly rate; that is, I restated everything in terms of how much of the entire task could be completed per hour. To do this, I simply inverted each value for "hours to complete job":

completed per hour:

Then, assuming that their per-hour rates were additive, I added the portion that each could do per hour, summed them, and set this equal to the "together" rate:

adding their labor:

As you can see in the above example, "work" problems commonly create rational equations . But the equations themselves are usually pretty simple to solve.

One pipe can fill a pool 1.25 times as fast as a second pipe. When both pipes are opened, they fill the pool in five hours. How long would it take to fill the pool if only the slower pipe is used?

My first step is to list the times taken by each pipe to fill the pool, and how long the two pipes take together. In this case, I know the "together" time, but not the individual times. One of the pipes' times is expressed in terms of the other pipe's time, so I'll pick a variable to stand for one of these times.

Advertisement

Since the faster pipe's time to completion is defined in terms of the second pipe's time, I'll pick a variable for the slower pipe's time, and then use this to create an expression for the faster pipe's time:

slow pipe: s

together: 5

Next, I'll convert all of the completion times to per-hour rates:

Then I make the necessary assumption that the pipes' contributions are additive (which is reasonable, in this case), add the two pipes' contributions, and set this equal to the combined per-hour rate:

multiplying through by 20 s (being the lowest common denominator of all the fractional terms):

20 + 25 = 4 s

45/4 = 11.25 = s

They asked me for the time of the slower pipe, so I don't need to find the time for the faster pipe. My answer is:

The slower pipe takes 11.25 hours.

Note: I could have picked a variable for the faster pipe, and then defined the time for the slower pipe in terms of this variable. If you're not sure how you'd do this, then think about it in terms of nicer numbers: If someone goes twice as fast as you, then you take twice as long as he does; if he goes three times as fast as you, then you take three times as long as him. In this case, if he goes 1.25 times as fast, then you take 1.25 times as long. So the variables could have been " f  " for the number of hours the faster pipe takes, and then the number of hours for the slower pipe would have been " 1.25 f  ".

URL: https://www.purplemath.com/modules/workprob.htm

Page 1 Page 2 Page 3 Page 4

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Visit Our Profiles

  The bold line represents the graph of the Aztec Company. The other line represents the graph of the Southern Company. The two lines intersect at the point where both companies are charging the same amount of money for monthly phone use, $125. This occurs at 500 minutes.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

Word Problems Involving Rates and Ratios

The ratio is to compare two numbers. Rate is one type of ratio and is used to measure the variety of one thing or quantity in comparison to other. Word problems involving comparing rates deal with distances, time, rates, wind or water current, money, and age.

A step-by-step guide to solving rates and ratios word problems

To solve the word problems involving rates and ratios, follow these steps: Step 1: Find the known ratio and the unknown ratio. Step 2: Write the proportion. Step 3: Use cross-multiply and solve. Step 4: Plug the result into the unknown ratio to check the answers.

Word Problems Involving Rates and Ratios – Examples 1

If 11 apple pies cost $88, what will 8 apple pies cost? Solution: Write as a rate. \(\frac{88÷11}{11÷11}=\frac{8}{1}\) Write a proportion to know the cost of 8 apple pies. \(\frac{8}{1}=\frac{x}{6}→8×6=1×x→x=48\)

Word Problems Involving Rates and Ratios – Examples 2

If 6 cookbooks cost $120, how much would a dozen cookbooks cost? Solution: Write as a rate. \(\frac{120÷6}{6÷6}=\frac{20}{1}\) Write a proportion to know the cost of 12 cookbooks. \(\frac{20}{1}=\frac{x}{12}→20×12=1×x→x=240\)

by: Effortless Math Team about 1 year ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• How to Graph Trigonometric Functions?
• Top 10 Tips to Create an ASTB Math Study Plan
• 4th Grade MAP Math FREE Sample Practice Questions
• Full-Length 7th Grade ACT Aspire Math Practice Test
• Tri-Fractional Operations: How to Add and Subtract Three Fractions with Different Denominators
• 3rd Grade MAP Math Practice Test Questions
• 3rd Grade NYSE Math FREE Sample Practice Questions
• 5 Best CHSPE Math Study Guides
• How to Find Missing Angles of Triangles
• Unlocking the Secrets of Triangle Angle Bisectors

What people say about "Word Problems Involving Rates and Ratios - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Solving Word Questions

With LOTS of examples!

In Algebra we often have word questions like:

Example: Sam and Alex play tennis.

On the weekend Sam played 4 more games than Alex did, and together they played 12 games.

How many games did Alex play?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if possible
• Assign letters for the values
• Find or work out formulas

You should also write down what is actually being asked for , so you know where you are going and when you have arrived!

Also look for key words:

Thinking Clearly

Some wording can be tricky, making it hard to think "the right way around", such as:

Example: Sam has 2 dollars less than Alex. How do we write this as an equation?

• Let S = dollars Sam has
• Let A = dollars Alex has

Now ... is that: S − 2 = A

or should it be: S = A − 2

or should it be: S = 2 − A

The correct answer is S = A − 2

( S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")

Example: on our street there are twice as many dogs as cats. How do we write this as an equation?

• Let D = number of dogs
• Let C = number of cats

Now ... is that: 2D = C

or should it be: D = 2C

Think carefully now!

The correct answer is D = 2C

( 2D = C is a common mistake, as the question is written "twice ... dogs ... cats")

Let's start with a really simple example so we see how it's done:

Example: A rectangular garden is 12m by 5m, what is its area ?

Turn the English into Algebra:

• Use w for width of rectangle: w = 12m
• Use h for height of rectangle: h = 5m

Formula for Area of a Rectangle : A = w × h

We are being asked for the Area.

A = w × h = 12 × 5 = 60 m 2

The area is 60 square meters .

Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?

• Use S for how many games Sam played
• Use A for how many games Alex played

We know that Sam played 4 more games than Alex, so: S = A + 4

And we know that together they played 12 games: S + A = 12

We are being asked for how many games Alex played: A

Which means that Alex played 4 games of tennis.

Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!

A slightly harder example:

Example: Alex and Sam also build tables. Together they make 10 tables in 12 days. Alex working alone can make 10 in 30 days. How long would it take Sam working alone to make 10 tables?

• Use a for Alex's work rate
• Use s for Sam's work rate

12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10

30 days of Alex alone is also 10 tables: 30a = 10

We are being asked how long it would take Sam to make 10 tables.

30a = 10 , so Alex's rate (tables per day) is: a = 10/30 = 1/3

Which means that Sam's rate is half a table a day (faster than Alex!)

So 10 tables would take Sam just 20 days.

Should Sam be paid more I wonder?

And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games. She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days. She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?

• The number of "5 hour" days: d
• The number of "3 hour" days: e

We know there are seven days in the week, so: d + e = 7

And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27

We are being asked for how many days she trains for 5 hours: d

The number of "5 hour" days is 3

Check : She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.

3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours

Some examples from Geometry:

Example: A circle has an area of 12 mm 2 , what is its radius?

• Use A for Area: A = 12 mm 2
• Use r for radius

And the formula for Area is: A = π r 2

We are being asked for the radius.

We need to rearrange the formula to find the area

Example: A cube has a volume of 125 mm 3 , what is its surface area?

Make a quick sketch:

• Use V for Volume
• Use A for Area
• Use s for side length of cube
• Volume of a cube: V = s 3
• Surface area of a cube: A = 6s 2

We are being asked for the surface area.

First work out s using the volume formula:

Now we can calculate surface area:

An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate. One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?

• Joel's normal rate of pay: $N per hour
• Joel works for 40 hours at $N per hour = $40N
• When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
• Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
• And together he earned $660, so:

$40N + $(12 × 1¼N) = $660

We are being asked for Joel's normal rate of pay $N.

So Joel’s normal rate of pay is $12 per hour

Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660

More about Money, with these two examples involving Compound Interest

Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?

This is the compound interest formula:

So we will use these letters:

• Present Value PV = $2,000
• Interest Rate (as a decimal): r = 0.11
• Number of Periods: n = 3
• Future Value (the value we want): FV

We are being asked for the Future Value: FV

Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33 What was the annual rate of interest for the savings account?

The compound interest formula:

• Present Value PV = $1,000
• Interest Rate (the value we want): r
• Number of Periods: n = 9
• Future Value: FV = $1,551.33

We are being asked for the Interest Rate: r

So the annual rate of interest is 5%

Check : $1,000 × (1.05) 9 = $1,000 × 1.55133 = $1,551.33

And an example of a Ratio question:

Example: At the start of the year the ratio of boys to girls in a class is 2 : 1 But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3 How many students are there altogether now?

• Number of boys now: b
• Number of girls now: g

The current ratio is 4 : 3

Which can be rearranged to 3b = 4g

At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1

b + 4 g − 2 = 2 1

Which can be rearranged to b + 4 = 2(g − 2)

We are being asked for how many students there are altogether now: b + g

There are 12 girls !

And 3b = 4g , so b = 4g/3 = 4 × 12 / 3 = 16 , so there are 16 boys

So there are now 12 girls and 16 boys in the class, making 28 students altogether .

There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3 At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1

And now for some Quadratic Equations :

Example: The product of two consecutive even integers is 168. What are the integers?

Consecutive means one after the other. And they are even , so they could be 2 and 4, or 4 and 6, etc.

We will call the smaller integer n , and so the larger integer must be n+2

And we are told the product (what we get after multiplying) is 168, so we know:

n(n + 2) = 168

We are being asked for the integers

That is a Quadratic Equation , and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.

Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES

Check 12: 12(12 + 2) = 12×14 = 168 YES

So there are two solutions: −14 and −12 is one, 12 and 14 is the other.

Note: we could have also tried "guess and check":

• We could try, say, n=10: 10(12) = 120 NO (too small)
• Next we could try n=12: 12(14) = 168 YES

But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).

Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side. Your client has 56 square meters of beautiful marble tiles to cover the whole area. What should the length of the room be?

Let's first make a sketch so we get things right!:

• the length of the room: L
• the width of the room: W
• the total Area including veranda: A
• the width of the room is half its length: W = ½L
• the total area is the (room width + 3) times the length: A = (W+3) × L = 56

We are being asked for the length of the room: L

This is a quadratic equation , there are many ways to solve it, this time let's use factoring :

And so L = 8 or −14

There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!

So the length of the room is 8 m

L = 8, so W = ½L = 4

So the area of the rectangle = (W+3) × L = 7 × 8 = 56

There we are ...

... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?

How Do You Solve a Word Problem Using Unit Rates?

Word problems allow you to see the real world uses of math! This tutorial shows you how to take a rate and convert it to a unit rate. Then, you can use that unit rate to calculate your answer. Watch this tutorial to learn all about it!

Background Tutorials

Decimal operation problems.

How Do You Multiply Decimals?

Doing math with paper and pencil can come in real handy, so make sure you're comfortable multiplying decimals by hand. After all, you don't want the calculator to be a crutch!

Ratio Definitions

What's a Ratio?

Ratios are everywhere! The scale on a map or blueprint is a ratio. Ingredients sometimes need to be mixed using ratios such as the ratio of water to cement mix when making cement. Watch this tutorial to learn about ratios. Then think of some ratios you've encountered before!

Using Rates and Unit Rates

How Do You Convert a Rate To A Unit Rate?

When you talk about the speed of a car, you usually say something in miles per hour. For example, you say, 'I drove 40 miles per hour.' Normally, you don't say, 'I drove 120 miles per 3 hours.' Figure out how to convert a rate like 120 miles per 3 hours to the unit rate of 40 miles per hour by watching this tutorial.

Further Exploration

Solving proportions.

How Do You Set Up a Proportion from a Word Problem?

Sometimes the hardest part of a word problem is figuring out how to turn the words into an equation you can solve. This tutorial let's you see the steps to take in order to turn a word problem involving a blueprint into a proportion. Take a look!

How Do You Solve a Word Problem Using a Proportion?

This tutorial provides a great real world application of math. You'll see how to use the scale from a blueprint of a house to help find the actual height of the house. This tutorial shows you how to use a proportion to solve!

• Terms of Use

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Distance Word Problems

Algebra topics  -, distance word problems, algebra topics distance word problems.

Algebra Topics: Distance Word Problems

Lesson 10: distance word problems.

/en/algebra-topics/introduction-to-word-problems/content/

What are distance word problems?

Distance word problems are a common type of algebra word problems. They involve a scenario in which you need to figure out how fast , how far , or how long one or more objects have traveled. These are often called train problems because one of the most famous types of distance problems involves finding out when two trains heading toward each other cross paths.

In this lesson, you'll learn how to solve train problems and a few other common types of distance problems. But first, let's look at some basic principles that apply to any distance problem.

The basics of distance problems

There are three basic aspects to movement and travel: distance , rate , and time . To understand the difference among these, think about the last time you drove somewhere.

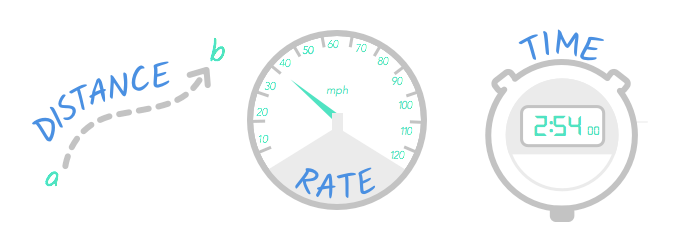
The distance is how far you traveled. The rate is how fast you traveled. The time is how long the trip took.

The relationship among these things can be described by this formula:

distance = rate x time d = rt

In other words, the distance you drove is equal to the rate at which you drove times the amount of time you drove. For an example of how this would work in real life, just imagine your last trip was like this:

• You drove 25 miles—that's the distance .
• You drove an average of 50 mph—that's the rate .
• The drive took you 30 minutes, or 0 .5 hours—that's the time .

According to the formula, if we multiply the rate and time , the product should be our distance.

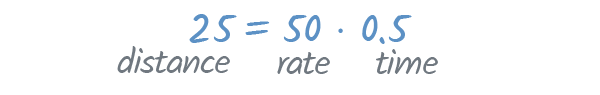
And it is! We drove 50 mph for 0.5 hours—and 50 ⋅ 0.5 equals 25 , which is our distance.

What if we drove 60 mph instead of 50? How far could we drive in 30 minutes? We could use the same formula to figure this out.

60 ⋅ 0.5 is 30, so our distance would be 30 miles.

Solving distance problems

When you solve any distance problem, you'll have to do what we just did—use the formula to find distance , rate , or time . Let's try another simple problem.

On his day off, Lee took a trip to the zoo. He drove an average speed of 65 mph, and it took him two-and-a-half hours to get from his house to the zoo. How far is the zoo from his house?

First, we should identify the information we know. Remember, we're looking for any information about distance, rate, or time. According to the problem:

• The rate is 65 mph.
• The time is two-and-a-half hours, or 2.5 hours.
• The distance is unknown—it's what we're trying to find.

You could picture Lee's trip with a diagram like this:

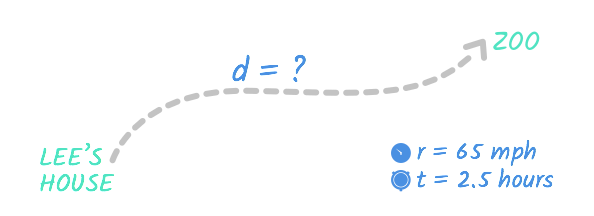
This diagram is a start to understanding this problem, but we still have to figure out what to do with the numbers for distance , rate , and time . To keep track of the information in the problem, we'll set up a table. (This might seem excessive now, but it's a good habit for even simple problems and can make solving complicated problems much easier.) Here's what our table looks like:

We can put this information into our formula: distance = rate ⋅ time .

We can use the distance = rate ⋅ time formula to find the distance Lee traveled.

The formula d = rt looks like this when we plug in the numbers from the problem. The unknown distance is represented with the variable d .

d = 65 ⋅ 2.5

To find d , all we have to do is multiply 65 and 2.5. 65 ⋅ 2.5 equals 162.5 .

We have an answer to our problem: d = 162.5. In other words, the distance Lee drove from his house to the zoo is 162.5 miles.

Be careful to use the same units of measurement for rate and time. It's possible to multiply 65 miles per hour by 2.5 hours because they use the same unit: an hour . However, what if the time had been written in a different unit, like in minutes ? In that case, you'd have to convert the time into hours so it would use the same unit as the rate.

Solving for rate and time

In the problem we just solved we calculated for distance , but you can use the d = rt formula to solve for rate and time too. For example, take a look at this problem:

After work, Janae walked in her neighborhood for a half hour. She walked a mile-and-a-half total. What was her average speed in miles per hour?

We can picture Janae's walk as something like this:

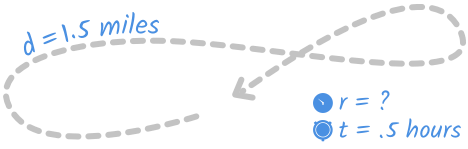
And we can set up the information from the problem we know like this:

The table is repeating the facts we already know from the problem. Janae walked one-and-a-half miles or 1.5 miles in a half hour, or 0.5 hours.

As always, we start with our formula. Next, we'll fill in the formula with the information from our table.

The rate is represented by r because we don't yet know how fast Janae was walking. Since we're solving for r , we'll have to get it alone on one side of the equation.

1.5 = r ⋅ 0.5

Our equation calls for r to be multiplied by 0.5, so we can get r alone on one side of the equation by dividing both sides by 0.5: 1.5 / 0.5 = 3 .

r = 3 , so 3 is the answer to our problem. Janae walked 3 miles per hour.

In the problems on this page, we solved for distance and rate of travel, but you can also use the travel equation to solve for time . You can even use it to solve certain problems where you're trying to figure out the distance, rate, or time of two or more moving objects. We'll look at problems like this on the next few pages.

Two-part and round-trip problems

Do you know how to solve this problem?

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph, then he drove on the interstate at an average of 70 mph. The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

This problem is a classic two-part trip problem because it's asking you to find information about one part of a two-part trip. This problem might seem complicated, but don't be intimidated!

You can solve it using the same tools we used to solve the simpler problems on the first page:

• The travel equation d = rt
• A table to keep track of important information

Let's start with the table . Take another look at the problem. This time, the information relating to distance , rate , and time has been underlined.

Bill took a trip to see a friend. His friend lives 225 miles away. He drove in town at an average of 30 mph , then he drove on the interstate at an average of 70 mph . The trip took three-and-a-half hours total. How far did Bill drive on the interstate?

If you tried to fill in the table the way we did on the last page, you might have noticed a problem: There's too much information. For instance, the problem contains two rates— 30 mph and 70 mph . To include all of this information, let's create a table with an extra row. The top row of numbers and variables will be labeled in town , and the bottom row will be labeled interstate .

We filled in the rates, but what about the distance and time ? If you look back at the problem, you'll see that these are the total figures, meaning they include both the time in town and on the interstate. So the total distance is 225 . This means this is true:

Interstate distance + in-town distance = Total distance

Together, the interstate distance and in-town distance are equal to the total distance. See?

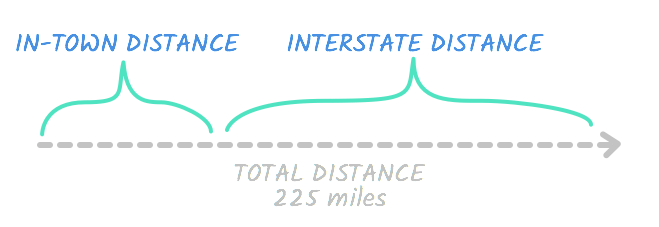
In any case, we're trying to find out how far Bill drove on the interstate , so let's represent this number with d . If the interstate distance is d , it means the in-town distance is a number that equals the total, 225 , when added to d . In other words, it's equal to 225 - d .

We can fill in our chart like this:

We can use the same technique to fill in the time column. The total time is 3.5 hours . If we say the time on the interstate is t , then the remaining time in town is equal to 3.5 - t . We can fill in the rest of our chart.

Now we can work on solving the problem. The main difference between the problems on the first page and this problem is that this problem involves two equations. Here's the one for in-town travel :

225 - d = 30 ⋅ (3.5 - t)

And here's the one for interstate travel :

If you tried to solve either of these on its own, you might have found it impossible: since each equation contains two unknown variables, they can't be solved on their own. Try for yourself. If you work either equation on its own, you won't be able to find a numerical value for d . In order to find the value of d , we'll also have to know the value of t .

We can find the value of t in both problems by combining them. Let's take another look at our travel equation for interstate travel.

While we don't know the numerical value of d , this equation does tell us that d is equal to 70 t .

Since 70 t and d are equal , we can replace d with 70 t . Substituting 70 t for d in our equation for interstate travel won't help us find the value of t —all it tells us is that 70 t is equal to itself, which we already knew.

But what about our other equation, the one for in-town travel?

When we replace the d in that equation with 70 t , the equation suddenly gets much easier to solve.

225 - 70t = 30 ⋅ (3.5 - t)

Our new equation might look more complicated, but it's actually something we can solve. This is because it only has one variable: t . Once we find t , we can use it to calculate the value of d —and find the answer to our problem.

To simplify this equation and find the value of t , we'll have to get the t alone on one side of the equals sign. We'll also have to simplify the right side as much as possible.

Let's start with the right side: 30 times (3.5 - t ) is 105 - 30 t .

225 - 70t = 105 - 30t

Next, let's cancel out the 225 next to 70 t . To do this, we'll subtract 225 from both sides. On the right side, it means subtracting 225 from 105 . 105 - 225 is -120 .

- 70t = -120 - 30t

Our next step is to group like terms—remember, our eventual goal is to have t on the left side of the equals sign and a number on the right . We'll cancel out the -30 t on the right side by adding 30 t to both sides. On the right side, we'll add it to -70 t . -70 t + 30 t is -40 t .

- 40t = -120

Finally, to get t on its own, we'll divide each side by its coefficient: -40. -120 / - 40 is 3 .

So t is equal to 3 . In other words, the time Bill traveled on the interstate is equal to 3 hours . Remember, we're ultimately trying to find the distanc e Bill traveled on the interstate. Let's look at the interstate row of our chart again and see if we have enough information to find out.

It looks like we do. Now that we're only missing one variable, we should be able to find its value pretty quickly.

To find the distance, we'll use the travel formula distance = rate ⋅ time .

We now know that Bill traveled on the interstate for 3 hours at 70 mph , so we can fill in this information.

d = 3 ⋅ 70

Finally, we finished simplifying the right side of the equation. 3 ⋅ 70 is 210 .

So d = 210 . We have the answer to our problem! The distance is 210 . In other words, Bill drove 210 miles on the interstate.

Solving a round-trip problem

It might have seemed like it took a long time to solve the first problem. The more practice you get with these problems, the quicker they'll go. Let's try a similar problem. This one is called a round-trip problem because it describes a round trip—a trip that includes a return journey. Even though the trip described in this problem is slightly different from the one in our first problem, you should be able to solve it the same way. Let's take a look:

Eva drove to work at an average speed of 36 mph. On the way home, she hit traffic and only drove an average of 27 mph. Her total time in the car was 1 hour and 45 minutes, or 1.75 hours. How far does Eva live from work?

If you're having trouble understanding this problem, you might want to visualize Eva's commute like this:

As always, let's start by filling in a table with the important information. We'll make a row with information about her trip to work and from work .

1.75 - t to describe the trip from work. (Remember, the total travel time is 1.75 hours , so the time to work and from work should equal 1.75 .)

From our table, we can write two equations:

• The trip to work can be represented as d = 36 t .
• The trip from work can be represented as d = 27 (1.75 - t ) .

In both equations, d represents the total distance. From the diagram, you can see that these two equations are equal to each other—after all, Eva drives the same distance to and from work .

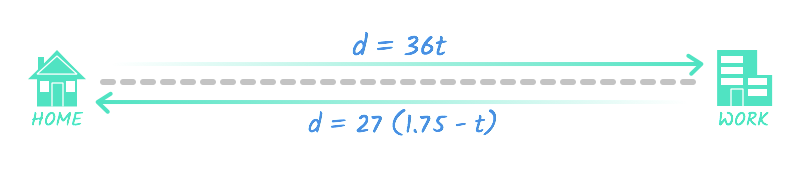
Just like with the last problem we solved, we can solve this one by combining the two equations.

We'll start with our equation for the trip from work .

d = 27 (1.75 - t)

Next, we'll substitute in the value of d from our to work equation, d = 36 t . Since the value of d is 36 t , we can replace any occurrence of d with 36 t .

36t = 27 (1.75 - t)

Now, let's simplify the right side. 27 ⋅(1.75 - t ) is 47.25 .

36t = 47.25 - 27t

Next, we'll cancel out -27 t by adding 27 t to both sides of the equation. 36 t + 27 t is 63 t .

63t = 47.25

Finally, we can get t on its own by dividing both sides by its coefficient: 63 . 47.25 / 63 is .75 .

t is equal to .75 . In other words, the time it took Eva to drive to work is .75 hours . Now that we know the value of t , we'll be able to can find the distance to Eva's work.

If you guessed that we were going to use the travel equation again, you were right. We now know the value of two out of the three variables, which means we know enough to solve our problem.

First, let's fill in the values we know. We'll work with the numbers for the trip to work . We already knew the rate : 36 . And we just learned the time : .75 .

d = 36 ⋅ .75

Now all we have to do is simplify the equation: 36 ⋅ .75 = 27 .

d is equal to 27 . In other words, the distance to Eva's work is 27 miles . Our problem is solved.

Intersecting distance problems

An intersecting distance problem is one where two things are moving toward each other. Here's a typical problem:

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading to Springfield at the same time a train leaves Springfield heading to Pawnee. One train is moving at a speed of 45 mph, and the other is moving 60 mph. How long will they travel before they meet?

This problem is asking you to calculate how long it will take these two trains moving toward each other to cross paths. This might seem confusing at first. Even though it's a real-world situation, it can be difficult to imagine distance and motion abstractly. This diagram might help you get a sense of what this situation looks like:

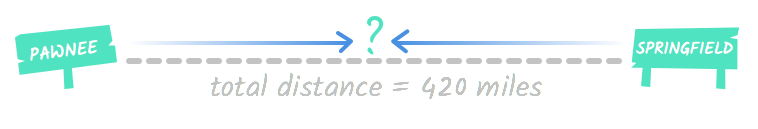
If you're still confused, don't worry! You can solve this problem the same way you solved the two-part problems on the last page. You'll just need a chart and the travel formula .

Pawnee and Springfield are 420 miles apart. A train leaves Pawnee heading toward Springfield at the same time a train leaves Springfield heading toward Pawnee. One train is moving at a speed of 45 mph , and the other is moving 60 mph . How long will they travel before they meet?

Let's start by filling in our chart. Here's the problem again, this time with the important information underlined. We can start by filling in the most obvious information: rate . The problem gives us the speed of each train. We'll label them fast train and slow train . The fast train goes 60 mph . The slow train goes only 45 mph .

We can also put this information into a table:

We don't know the distance each train travels to meet the other yet—we just know the total distance. In order to meet, the trains will cover a combined distance equal to the total distance. As you can see in this diagram, this is true no matter how far each train travels.

This means that—just like last time—we'll represent the distance of one with d and the distance of the other with the total minus d. So the distance for the fast train will be d , and the distance for the slow train will be 420 - d .

Because we're looking for the time both trains travel before they meet, the time will be the same for both trains. We can represent it with t .

The table gives us two equations: d = 60 t and 420 - d = 45 t . Just like we did with the two-part problems, we can combine these two equations.

The equation for the fast train isn't solvable on its own, but it does tell us that d is equal to 60 t .

The other equation, which describes the slow train, can't be solved alone either. However, we can replace the d with its value from the first equation.

420 - d = 45t

Because we know that d is equal to 60 t , we can replace the d in this equation with 60 t . Now we have an equation we can solve.

420 - 60t = 45t

To solve this equation, we'll need to get t and its coefficients on one side of the equals sign and any other numbers on the other. We can start by canceling out the -60 t on the left by adding 60 t to both sides. 45 t + 60 t is 105 t .

Now we just need to get rid of the coefficient next to t . We can do this by dividing both sides by 105 . 420 / 105 is 4 .

t = 4 . In other words, the time it takes the trains to meet is 4 hours . Our problem is solved!

If you want to be sure of your answer, you can check it by using the distance equation with t equal to 4 . For our fast train, the equation would be d = 60 ⋅ 4 . 60 ⋅ 4 is 240 , so the distance our fast train traveled would be 240 miles. For our slow train, the equation would be d = 45 ⋅ 4 . 45 ⋅ 4 is 180 , so the distance traveled by the slow train is 180 miles . Remember how we said the distance the slow train and fast train travel should equal the total distance? 240 miles + 180 miles equals 420 miles , which is the total distance from our problem. Our answer is correct.

Practice problem 1

Here's another intersecting distance problem. It's similar to the one we just solved. See if you can solve it on your own. When you're finished, scroll down to see the answer and an explanation.

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove an average of 70 mph. How long did they drive before they met up?

Problem 1 answer

Here's practice problem 1:

Jon and Dani live 270 miles apart. One day, they decided to drive toward each other and hang out wherever they met. Jon drove an average of 65 mph, and Dani drove 70 mph. How long did they drive before they met up?

Answer: 2 hours .

Let's solve this problem like we solved the others. First, try making the chart. It should look like this:

Here's how we filled in the chart:

• Distance: Together, Dani and Jon will have covered the total distance between them by the time they meet up. That's 270 . Jon's distance is represented by d , so Dani's distance is 270 - d .
• Rate: The problem tells us Dani and Jon's speeds. Dani drives 65 mph , and Jon drives 70 mph .
• Time: Because Jon and Dani drive the same amount of time before they meet up, both of their travel times are represented by t .

Now we have two equations. The equation for Jon's travel is d = 65 t . The equation for Dani's travel is 270 - d = 70 t . To solve this problem, we'll need to combine them.

The equation for Jon tells us that d is equal to 65 t . This means we can combine the two equations by replacing the d in Dani's equation with 65 t .

270 - 65t = 70t

Let's get t on one side of the equation and a number on the other. The first step to doing this is to get rid of -65 t on the left side. We'll cancel it out by adding 65 t to both sides: 70 t + 65 t is 135 t .

All that's left to do is to get rid of the 135 next to the t . We can do this by dividing both sides by 135 : 270 / 135 is 2 .

That's it. t is equal to 2 . We have the answer to our problem: Dani and Jon drove 2 hours before they met up.

Overtaking distance problems

The final type of distance problem we'll discuss in this lesson is a problem in which one moving object overtakes —or passes —another. Here's a typical overtaking problem:

The Hill family and the Platter family are going on a road trip. The Hills left 3 hours before the Platters, but the Platters drive an average of 15 mph faster. If it takes the Platter family 13 hours to catch up with the Hill family, how fast are the Hills driving?

You can picture the moment the Platter family left for the road trip a little like this:

The problem tells us that the Platter family will catch up with the Hill family in 13 hours and asks us to use this information to find the Hill family's rate . Like some of the other problems we've solved in this lesson, it might not seem like we have enough information to solve this problem—but we do. Let's start making our chart. The distance can be d for both the Hills and the Platters—when the Platters catch up with the Hills, both families will have driven the exact same distance.

Filling in the rate and time will require a little more thought. We don't know the rate for either family—remember, that's what we're trying to find out. However, we do know that the Platters drove 15 mph faster than the Hills. This means if the Hill family's rate is r , the Platter family's rate would be r + 15 .

Now all that's left is the time. We know it took the Platters 13 hours to catch up with the Hills. However, remember that the Hills left 3 hours earlier than the Platters—which means when the Platters caught up, they'd been driving 3 hours more than the Platters. 13 + 3 is 16 , so we know the Hills had been driving 16 hours by the time the Platters caught up with them.

Our chart gives us two equations. The Hill family's trip can be described by d = r ⋅ 16 . The equation for the Platter family's trip is d = ( r + 15) ⋅ 13 . Just like with our other problems, we can combine these equations by replacing a variable in one of them.

The Hill family equation already has the value of d equal to r ⋅ 16. So we'll replace the d in the Platter equation with r ⋅ 16 . This way, it will be an equation we can solve.

r ⋅ 16 = (r + 15) ⋅ 13

First, let's simplify the right side: r ⋅ 16 is 16 r .

16r = (r + 15) ⋅ 13

Next, we'll simplify the right side and multiply ( r + 15) by 13 .

16r = 13r + 195

We can get both r and their coefficients on the left side by subtracting 13 r from 16 r : 16 r - 13 r is 3 r .

Now all that's left to do is get rid of the 3 next to the r . To do this, we'll divide both sides by 3: 195 / 3 is 65 .

So there's our answer: r = 65. The Hill family drove an average of 65 mph .

You can solve any overtaking problem the same way we solved this one. Just remember to pay special attention when you're setting up your chart. Just like the Hill family did in this problem, the person or vehicle who started moving first will always have a greater travel time.

Practice problem 2

Try solving this problem. It's similar to the problem we just solved. When you're finished, scroll down to see the answer and an explanation.

A train moving 60 mph leaves the station at noon. An hour later, a train moving 80 mph leaves heading the same direction on a parallel track. What time does the second train catch up to the first?

Problem 2 answer

Here's practice problem 2:

Answer: 4 p.m.

To solve this problem, start by making a chart. Here's how it should look:

Here's an explanation of the chart:

• Distance: Both trains will have traveled the same distance by the time the fast train catches up with the slow one, so the distance for both is d .
• Rate: The problem tells us how fast each train was going. The fast train has a rate of 80 mph , and the slow train has a rate of 60 mph .
• Time: We'll use t to represent the fast train's travel time before it catches up. Because the slow train started an hour before the fast one, it will have been traveling one hour more by the time the fast train catches up. It's t + 1 .

Now we have two equations. The equation for the fast train is d = 80 t . The equation for the slow train is d = 60 ( t + 1) . To solve this problem, we'll need to combine the equations.

The equation for the fast train says d is equal to 80 t . This means we can combine the two equations by replacing the d in the slow train's equation with 80 t .

80t = 60 (t + 1)

First, let's simplify the right side of the equation: 60 ⋅ ( t + 1) is 60 t + 60 .

80t = 60t + 60

To solve the equation, we'll have to get t on one side of the equals sign and a number on the other. We can get rid of 60 t on the right side by subtracting 60 t from both sides: 80 t - 60 t is 20 t .

Finally, we can get rid of the 20 next to t by dividing both sides by 20 . 60 divided by 20 is 3 .

So t is equal to 3 . The fast train traveled for 3 hours . However, it's not the answer to our problem. Let's look at the original problem again. Pay attention to the last sentence, which is the question we're trying to answer.

Our problem doesn't ask how long either of the trains traveled. It asks what time the second train catches up with the first.

The problem tells us that the slow train left at noon and the fast one left an hour later. This means the fast train left at 1 p.m . From our equations, we know the fast train traveled 3 hours . 1 + 3 is 4 , so the fast train caught up with the slow one at 4 p.m . The answer to the problem is 4 p.m .

/en/algebra-topics/algebra-quiz/content/

Wind and Current Word Problems

Related Topics: More Lessons for Algebra II Math Worksheets

Videos, worksheets, solutions and activities to help Algebra 1 students learn how to solve wind and current word problems.

Rate of current problem #2 Shows how to solve a word problem involving the rate of a current and rowing in still water using 2 variables and 2 linear equations. Example: A dolphin swimming against an ocean current traveled 60 miles in 2 hours. It then turned around to swim with the current and was able to get back to its starting place in 1.5 hours. Find the speed of the dolphin in still water and the rate of the current.

Wind and Current Problems How to solve wind and current word problems using 2 variables and a system of linear equations? What happens to the rate when the wind is at your back? What happens when you try to paddle a kayak upstream? Examples: (1) A plane can fly 3750 km in 3 hours with the wind. The plane takes 5 hours to travel the same distance against the same wind speed. Find the rate of the plane in still air. Find the speed of the wind. (2) Jim can ow a boat 30 km downstream in 3 hours, but it takes him 5 hours to return. What is his rate in still water? What is the rate of the current?

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Calcworkshop

How to Solve d=rt Word Problems? 5 Amazing Examples!

// Last Updated: January 20, 2020 - Watch Video //

An object is said to be in uniform motion when it moves without changing its speed.

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)

All this means is that we can find the distance an object travels as long as we know the object is moving at a constant (fixed) speed or pace or at an average rate or speed.

In fact, whenever we encounter this type of scenario we can utilize a very powerful formula:

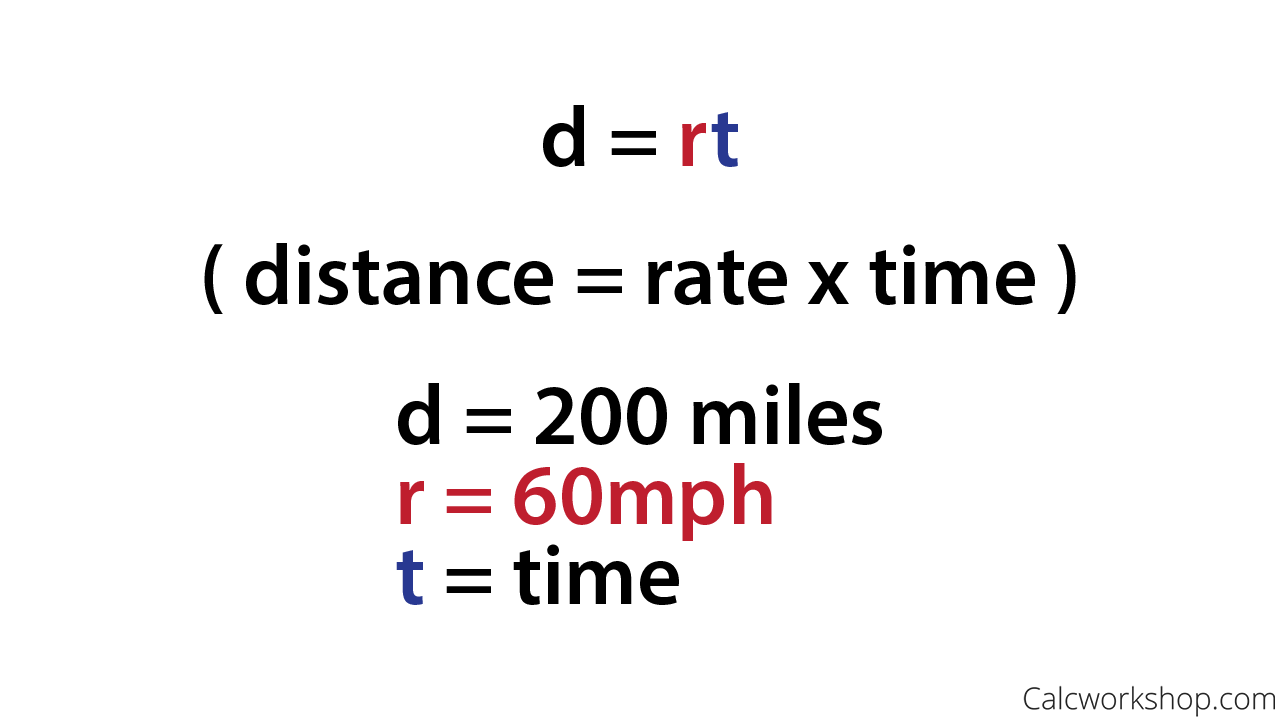
Distance-Rate-Time Example

• d represents distance
• r is an object’s rate (speed)
• t is the time the object takes to travel

The type of questions we will be investigating in this lesson involve:

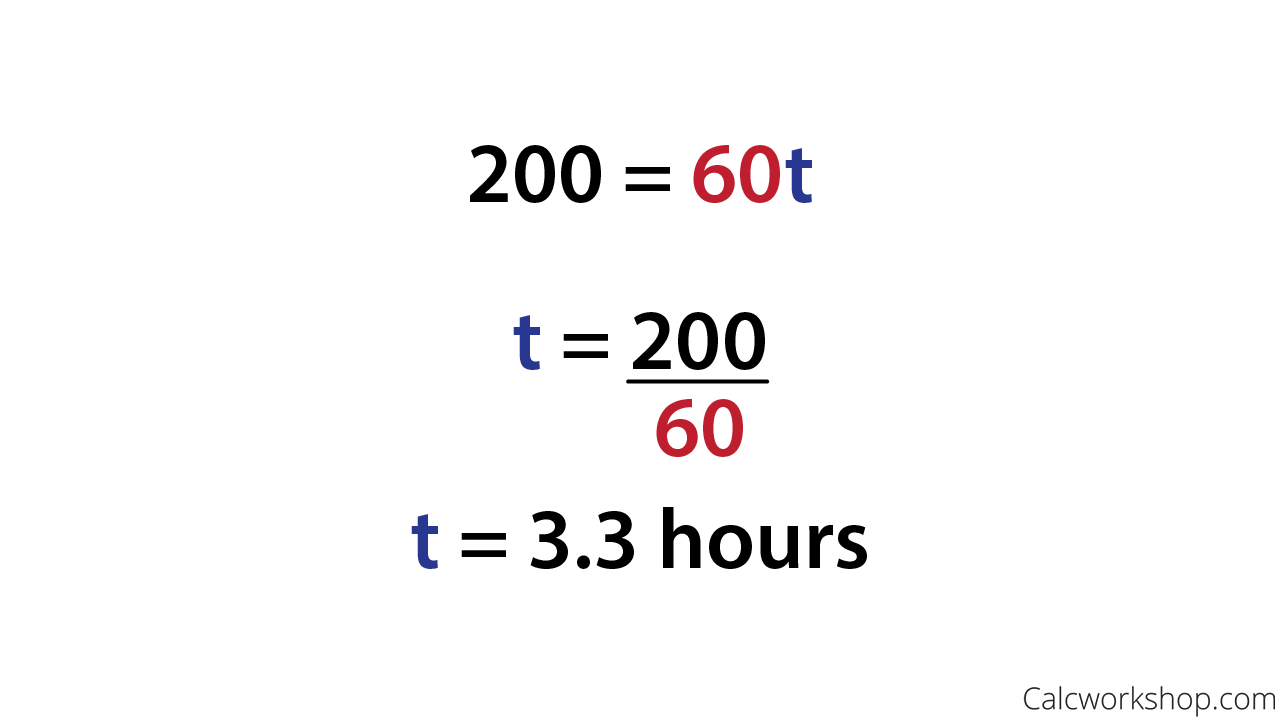
Solving Distance Rate Time Example

And all three of these questions can be answered using the Distance formula listed above.

Yes, it is simple, but there is a warning.

Units of measure matter!

As Purple Math so accurately points out, we must always check our units to ensure they agree with one another.

Many questions will try to trick you by using miss-matched units, so always check and if necessary, convert to the correct unit before simplifying.

Together we will look at five examples in detail for how to solve Distance-Rate-Time word problems.

Number Line

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• Middle School Math Solutions – Simultaneous Equations Calculator Solving simultaneous equations is one small algebra step further on from simple equations. Symbolab math solutions...

Please add a message.

Message received. Thanks for the feedback.

WuKong Blog

Popular searches

How to Solve Math Word Problems: 10 Effective Strategies

Ever been stuck on a tricky problem, wondering how to untangle the mess of words? Imagine you’re trying to figure out how many apples someone ends up with after getting a few more. Don’t worry; we’ve got your back! In this article, we’ll guide you through simple yet powerful strategies to tackle these mind-bending puzzles effortlessly. With clear examples and easy steps, we’ll show you how to master the art of problem-solving. So, are you ready to crack the code and become a word problem-solving pro? Let’s dive in and explore the secrets together!

Wukong Math provides online word problem materials for Grades K-12 students , and interested parents can download them for their children. By the way, You can get more download permissions after making a free reservation for a trial class.

10 Effective Strategies to Solve Word Problems

Solving word problems may seem daunting at first, but with the right strategies, you can navigate through them smoothly. Here are ten effective strategies to help you conquer word problems and become a master problem-solver:

1. Understand the Problem

Understanding its context and requirements is the cornerstone of solving any word problem. The first step in tackling a word problem is carefully reading and understanding the problem statement. Identify the key components, including:

• What is known: Recognize the information provided in the problem.
• What is unknown: Determine what needs to be found or solved.
• Keywords: Pay attention to words that signal mathematical operations (e.g., “sum,” “difference,” “product,” “quotient”).

Example: Suppose you’re given a problem: “If Sally has 5 more apples than Tom, and Tom has 7 apples, how many apples does Sally have?” Identify the given information (Tom has 7 apples) and the unknown (the number of apples Sally has).

2. Draw a Diagram or Model

Visual aids can provide invaluable insights into word problems, aiding comprehension and solution formulation. Draw diagrams or models to represent the problem visually, depicting quantities, relationships, and relevant information. This visual representation can help clarify the problem and guide the solution process.

Example: Consider a problem involving the division of a pizza among friends. Drawing a circle to represent the pizza and dividing it into equal slices can help visualize the distribution process and determine each person’s share accurately.

3. Use Logical Reasoning

Logical reasoning is a powerful tool for problem-solving, enabling you to analyze the problem systematically and deduce the most appropriate solution method. Look for patterns, relationships, or constraints within the problem to guide your approach. Logical reasoning can streamline the problem-solving process and lead to efficient solutions.

Example: In a problem where you’re asked to determine the number of legs in a group of animals, logically deduce that each animal has a certain number of legs based on its species (e.g., dogs have four legs, birds have two legs), and count accordingly.

4. Break it Down

Complex word problems can often be overwhelming at first glance. Breaking the problem into smaller, more manageable parts can simplify the problem-solving process. Solve each part individually, focusing on one aspect at a time, before combining the solutions to arrive at the final answer.

Example: To find the total cost of purchasing multiple items, break down the problem into calculating the cost of each item individually. Then, sum up the costs to find the total expenditure.

Steps for “Break it Down” Strategy:

Step 1: Identify the components or parts of the problem.

Step 2: Solve each part separately, addressing one aspect at a time.

Step 3: Ensure accuracy in each solution.

Step 4: Combine the solutions of the individual parts to find the overall solution.

5. Guess and Check

The guess and check strategy involves making educated guesses and testing them to see if they fit the problem conditions. Adjust your approach based on the results until you find the correct solution. This iterative process helps refine your understanding of the problem and leads you closer to the solution.

Example: When determining the number of marbles in a jar, make an initial guess based on visual estimation. Count the marbles to check if your guess is close. Adjust your guess accordingly until you arrive at the correct number.

6. Use Algebraic Equations

Translating word problems into algebraic equations can provide a systematic approach to solving complex problems. Assign variables to unknown quantities, and use mathematical operations to express relationships between the variables. Solving the resulting equations yields the solution to the problem.

Example: Suppose you’re asked to find two consecutive numbers whose sum is 15. Represent the numbers as x and x + 1 (since they are consecutive). Then, write the equation x + (x + 1) = 15 and solve for x to find the two numbers.

7. Work Backwards

Starting with the desired outcome and working backward can be an effective strategy for solving word problems, especially those involving sequences or processes. Determine the final result and trace back the steps or operations needed to achieve that result. This approach helps simplify the problem by breaking it down into sequential steps.

Example: If you need to determine the original price of an item after a series of discounts, start with the discounted price and apply the reverse of each discount until you reach the original price. This process allows you to backtrack through the discounts and arrive at the initial cost.

8. Look for Patterns

Many word problems exhibit recurring patterns or structures that can be leveraged to streamline the problem-solving process. Identify these patterns by analyzing the problem statement and recognizing similarities or repetitions. Once identified, exploit these patterns to simplify calculations and derive solutions more efficiently.

Example: Recognize common patterns in sequences, such as arithmetic or geometric progressions, to predict the next term or find missing elements. By identifying the underlying pattern, you can extrapolate the solution with confidence.

9. Use Concrete Examples

Substituting concrete values into the problem can help clarify its underlying structure and facilitate solution development. Replace abstract variables with specific numbers to illustrate the problem-solving process step by step. Once you understand the methodology with concrete examples, apply it to solve the original problem.

Example: Instead of solving a problem with abstract variables, substitute specific numbers to demonstrate the solution process. For instance, in a problem involving percentages, use concrete values such as 50% or 75% to elucidate the calculation steps.

10. Practice, Practice, Practice

Regular practice is key to mastering the art of solving word problems. Engage in frequent problem-solving exercises to familiarize yourself with different problem types and solution methods. As you practice, you’ll develop fluency in identifying problem-solving strategies and applying them effectively to diverse scenarios.

Discover WuKong Math : Where Students Excel in Math Word Problem-Solving

At WuKong Math, our goal is to unleash the hidden math genius within every student. Our innovative teaching method aims to reignite a passion for numbers and problem-solving, catering to students globally from grades 1 to 12. Through live math classes facilitated by seasoned instructors, we strive to bring back the excitement of mastering mathematical concepts and tackling word problems .

Course Highlights:

• Live Instruction: Experienced math instructors lead engaging classes, blending live instruction with interactive online sessions.
• Global Availability: With courses spanning all 24 time zones, students worldwide can access top-notch math education.
• Copyrighted Curriculum: WuKong Math offers proprietary courses with a clear grading system, ensuring comprehensive learning.
• Vast Math Resources : WuKong Math provides access to hundreds of original math learning resources besides live classes. These resources cover various topics and offer supplementary materials to reinforce learning and provide additional practice.

Course Benefits:

• World-Class Educators: Their team of math teachers hails from prestigious universities worldwide, bringing years of experience and a passion for igniting students’ love for learning.
• Advanced Enrichment: Tailored to students of varying backgrounds, their 10-level enrichment courses enhance mathematical thinking skills, preparing students for success in competitions and exams.
• Innovative Teaching Methods: WuKong incorporates Singapore’s CPA modeling approach, fostering creative problem-solving skills and making math fun through interactive, game-style challenges.
• International Accreditation: Recognized by Cognia®, WuKong Math offers students the opportunity to earn internationally accredited transcripts and certificates, opening doors to prestigious institutions worldwide.

FAQs on Solving Word Problems

Q1. what are word problems.

Word problems are mathematical questions presented in a textual format, often involving real-world scenarios that require mathematical operations to solve.

Q2. Why do students often struggle with solving word problems?

Students may find word problems challenging due to difficulties in understanding the problem statement, identifying relevant information, and translating it into mathematical operations accurately.

Q3. How can teachers support students in mastering word problem solving?

Teachers can provide scaffolded instruction, offer ample practice opportunities, use real-life contexts, and provide feedback tailored to individual student needs to enhance their proficiency in solving word problems.

Q4. What are the benefits of mastering word problem-solving skills?

Proficiency in solving word problems fosters critical thinking, analytical reasoning, and problem-solving abilities, which are essential skills applicable in various academic disciplines and real-life situations.

Conclusion:

In this article, we’ve explored the essential skill of solving word problems. From understanding the problem to employing effective strategies like drawing diagrams and using logical reasoning, we’ve uncovered the secrets to mastering math challenges. For those seeking further guidance, WuKong Math emerges as a comprehensive solution, offering live classes, innovative teaching methods, and abundant resources. With WuKong Math , students worldwide can enhance their problem-solving skills, excel in mathematics, and ignite a passion for learning. Take the next step towards math proficiency and join the WuKong Math community today!

Delvair holds a degree in Physics from the Federal University of Maranhão, Brazil. With over six years of experience, she specializes in teaching mathematics, with a particular emphasis on Math Kangaroo competitions. She firmly believes that education is the cornerstone of society’s future. Additionally, she holds the conviction that every child can learn given the right environment and guidance. In her spare time, she enjoys singing and tending to her plants.

• Previous Top 7 Online Homeschool Math Curriculum & Program for PreK-12 [2024]
• Next Top 40 Hilarious Math Memes for Kids & Teens in 2024

Delvair holds a degree in Physics from the Federal University of Maranhão, Brazil. With over six years of experience, she specializes in teaching mathematics, with a particular emphasis on Math Kangaroo competitions. She firmly believes that education is the cornerstone of society's future. Additionally, she holds the conviction that every child can learn given the right environment and guidance. In her spare time, she enjoys singing and tending to her plants.

Asian American and Pacific Islander Heritage Month: History & Celebration

2nd grade reading comprehension: tips for success, wukong chinese review: authentic insights from overseas parents and authority platform evaluations, top 5 platforms for affordable chinese classes for kids online, how to learn chinese characters: a step-by-step guide, how to learn abacus maths at home [2024 guide], wukong education "tell us your abc story" award-winning story: the last conversation, wukong education "tell us your abc story" award-winning story: saturday school, a comprehensive guide for gearing up for the 2024 dmmc, comprehensive guide of 15 ways to say thank you in chinese in any situation (with pronunciation）, chinese horoscope 2024: prediction, lucky, health, wealth, how do you say hello in chinese -a full guide, 5 best platforms for online english classes - expert reviews & insights, top 5 english  classes for kids- 7 easy tips for kids to improve english.

• AMC 10 2023
• when will STAAR test results be released 2023
• What is ERB Testing?
• math learning
• WuKong Math
• Passing score for STAAR
• Basic Math Skills PDFs
• Math Kangaroo Contest 2024
• Interpreting ERB Scores
• Recent Posts
• Popular Posts
• Recent Comments

Chinese Phrases

How to Find Perimeter: Easy Steps & Practical Examples

Perimeter: Formula, Definition, Examples, Math Steps, Shapes

Math Learning

Top 40 Hilarious Math Memes for Kids & Teens in 2024

Top 7 Online Homeschool Math Curriculum & Program for PreK-12 [2024]

Mental Strategies to Overcome Mathematics Difficulties: Helping Young Learners Establish a Positive Learning Attitude

Chinese Learning

Dragon Boat Festival 2024: Origin, Traditions, Celebrations

Math Learning / Education News / Math Education

Math Tests for 5th Graders: Question, Answer, Tips [2024 Updated]

English Tutoring / English Education / Learning Tips

Top 5 Websites to Learn ELA Online- You’re Complete Guide to English Mastery

4 Recommended Free Math Courses Online

• 24 Solar Terms Alphabet in Chinese AMC 10 2023 problems and answers Awakening of Insects Basic Math Skills book donation celebrate Hanukkah 2024 Chinese Chinese Alphabet chinese birthday wishes for mother Chinese culture Chinese festival Chinese learning Chinese Learning Online Chinese Learning Tips ChingMing Festival Dragon Boat Festival EdTech EdTechX English Learning Greeting cards for New year's day happy birthday message in chinese Language learning love in chinese traditional math calculation math games math kangaroo CA Math Kangaroo Competition Math Kangaroo Contest Math Kangaroo Contest 2023 Math Kangaroo Contest 2024 Math Kangaroo History Math Kangaroo USA math learning math learning games my love in chinese my love in chinese cantonese The New York Times Student Editorial Contest Valentine's Day when will STAAR test results be released 2023 WuKong Chinese WuKong Education WuKong Math WuKongMath 二十四节气之惊蛰

WuKong Recommends

Chinese Zodiac Years

How to Speak Chinese Fluently: The Ultimate Guide for Beginners

How to Pronounce Chinese Numbers: A Beginner's Guide for 2024

2023 & 2024 AP Chinese Language and Culture Exam: Date, Format, Questions and PracticeTips