singapore problem solving method

Bar Modelling

Bar modelling is an essential maths mastery strategy. A Singapore-style of maths model, bar modelling allows pupils to draw and visualize mathematical concepts to solve problems.

At a glance

• A versatile maths model strategy that can be used across a wide range of concepts and topics
• Gives pupils a powerful and adaptable strategy for solving increasingly difficult problems
• Allows pupils to understand on a conceptual level what occurs when using complex formulas (for example, algebra)
• Draws on the Concrete, Pictorial, Abstract approach
• Used extensively in Singapore-style maths mastery textbooks and workbooks
• Based on three pedagogical theorists — Jerome Bruner, Zoltan Dienes, and Alan J Bishop

Bar modelling and the CPA approach

The bar model method draws on the Concrete, Pictorial, Abstract (CPA) approach — an essential maths mastery concept. The process begins with pupils exploring problems via concrete objects. Pupils then progress to drawing pictorial diagrams, and then to abstract algorithms and notations (such as the +, -, x and / symbols).

The example below explains how bar modelling moves from concrete maths models to pictorial representations.

As shown, the bar method is primarily pictorial. Pupils will naturally develop from handling concrete objects, to drawing pictorial representations, to creating abstract rectangles to illustrate a problem. With time and practice, pupils will no longer need to draw individual boxes/units. Instead, they will label one long rectangle/bar with a number. At this stage, the bars will be somewhat proportional. So, in the example above, the purple bar representing 12 cookies is longer than the orange bar representing 8 cookies.

The lasting advantages of bar modelling

On one hand, the Singapore maths model method — bar modelling — provides pupils with a powerful tool for solving word problems. However, the lasting power of bar modelling is that once pupils master the approach, they can easily use bar models year after year across many maths topics. For example, bar modelling is an excellent technique (but not the only one!) for tackling ratio problems, volume problems, fractions, and more.

Importantly, bar modelling leads students down the path towards mathematical fluency and number sense. Maths models using concrete or pictorial rectangles allow pupils to understand complex formulas (for example, algebra) on an intuitive, conceptual level. Instead of simply following the steps of any given formula, students will possess a strong understanding of what is actually happening when applying or working with formulas.

The result? A stable, transferable, and solid mathematical framework for approaching abstract concepts. Combined with other [ Error: Link is empty → essential maths mastery strategies and concepts ← ] (https://mathsnoproblem.com/en/approach/number-bonds/), bar modelling sets students up for long-term maths success.

Find out how proven mastery strategies, world-class training, and step-by-step teacher guides can give you and your school a maths boost.

Share your success, be rewarded.

Everyone needs a break. Especially the kids that are missing out.

By clicking “Accept All” , you agree to the storing of cookies on your device to enhance site navigation, analyze site usage and assist in our marketing efforts.

Singapore Math

Looking for Singapore Math help? We have a collection of video lessons, examples and solutions, activities and worksheets that are based on Singapore Math or Maths.

Related Pages Word Problems Solved The Singapore Math Way 2-Step Word Problems And Bar Models Singapore Mental Math Strategies Math Games Math Worksheets

We will look at:

• What is Singapore Math or Maths?
• Using Singapore Math to solve word problems.
• Singapore Math from Grade 1 to Grade 6 (Videos and Worksheets).

What Is Singapore Math?

Introduction to Singapore Math Part 1. What are the benefits and strategies of Singapore Math? What are number bonds?

How To Use Model Drawing?

Introduction to Singapore Math Part 2.

Examples: (1) Carla and Jerome kept track of the miles they ran over the weekend. Carla ran three times as far as Jerome. If Carla ran 6 miles, how far did Jerome run?

(2) Mrs. Walsh made 300 cookies. She sold 3/4 of them and gave 1/3 of the remainder to her neighbor. How many cookies were left?

Helping Parents Explain Singapore Math - Word Problems 1

Demo for parents and educators on how to use “thinking blocks” (block diagrams) to help even young children - 1st grade, 2nd grade - understand, model and solve word problems.

Examples: (1) David has 45 marbles. His sister gave him 32 more. How many marbles does he have altogether?

(2) Caleb wants to buy a scooter that costs $63. He saved $38 so far. How much more money does Caleb need?

Helping Parents Explain Singapore Math - Word Problems 2

Part 2: 2-Step Word Problems.

Examples: (1) Anna is riding in a bike-a-thon. She rode 49 miles in the morning, stopped for a lunch break, then rode another 37 miles in the afternoon. Anna was then only 62 miles from the finish line. How long was Anna’s bike ride?

(2) Kierka bought a juice for 55 cents, a breakfast bar for 27 cents and a package of gum. She spent $1.22 altogether. How much did the package of gum cost?

Solve Word Problems Using Singapore Math: By Topics

These lessons and videos show how to use the block models (tape diagrams or bar models) in the Singapore Math method of solving word problems. The blocks can assist the students in visualizing, modeling and solving the word problems without using algebra.

Addition Word Problems (1-step word problems) Addition Word Problems (2-step word problems) Subtraction Word Problems (1-step word problems) Subtraction Word Problems (2-step word problems) Addition & Subtraction Word Problems (2 or 3 steps) Addition & Subtraction Word Problems (2 or 3 amounts) Multiplication Word Problems (1-step word problems) Multiplication Word Problems (2-step word problems) Multiplication Word Problems (comparing 2 or 3 amounts) Division Word Problems (1-step word problems) Division Word Problems (2-step word problems) Mixed Operations Word Problems (3-steps) Solving Challenging Word Problems (mixed operations) Fraction Word Problems (introductory) Fraction Word Problems (intermediate) Fraction Word Problems (difficult) Decimal Word Problems (1-step word problems) Decimal Word Problems (2-step word problems) Decimal Word Problems (difficult) Percent Word Problems Ratio Word Problems Algebraic Reasoning Problem Sums

Solve Word Problems Using Singapore Math: By Grades

2nd Grade Word Problems: 1-step Addition, Subtraction, Multiplication & Division Word Problems: Time, Fraction Word Problems: Model Drawing, Addition Model

3rd Grade Word Problems (2-step Addition & Subtraction) 3rd Grade Word Problems (2-step Multiplication & Division) Grade 3 Basic Word Problems 2-Step Word Problems and Bar Models Grade 3 Solving Word Problems using Bar Models Grade 3 More Word Problems: Multiplication, Mass, Time 4th Grade Word Problems (3-step Mixed Operations) 4th Grade Word Problems: time, weight, volume, measures

5th Grade Word Problems (Ratios & Proportions) 5th Grade Word Problems (Percent) Ratio (Equivalent Ratios, Simplify) Data Analysis (Average) Measurements (Triangles, Cubes & Cuboids) Grade 5 Word Problems Fraction Word Problems Whole Numbers Word Problems 1 - 4 Whole Numbers Word Problems 5 - 8 Whole Numbers Word Problems 9 - 12 Whole Numbers Word Problems 13 -16 Whole Numbers Word Problems 17 - 20 Whole Numbers Word Problems 21 - 23 Ratio & Proportion Word Problems Percent Word Problems 1 - 4 Fraction, Discount, Prices, Tax. Percent Word Problems 5 - 8 Banking Principles, Measurement (length), Convert Percent to Fraction. Decimal Word Problems 1 - 4 Subtraction of two decimals and unit conversion, Measurement using decimals to explain unit conversion. Decimal Word Problems 5 - 8 Multiplying decimals by 10s and rounding off decimals, Word problems involving decimals, fractions and measurement, Compare decimals involving measurement (volume). Decimal Word Problems 9 - 11 A measurement (area) word problem involving decimals, Word problems involving measurement (mass) and unit conversion.

6th Grade Word Problems (Ratios & Fractions) 6th Grade Word Problems (Ratios & Proportions) 6th Grade Word Problems (Percent) 6th Grade Word Problems (Average Speed) Elementary and Intermediate Word Problems Advanced Word Problems Grade 6 Word Problems 1 - 4 Simplifying Algebraic Expressions, Average Speed, Circles, Triangles and 4-sided figures. Grade 6 Word Problems 5 - 11 Venn Diagrams, More Challenging Word Problems, Heuristic Approach to Problem Solving. Data Analysis Read, make and interpret pie charts, Solve 1-step word problems using information presented in a pie chart. Grade 6 Geometry Volume of Cubes and Cuboids word problems.

7th Grade Word Problems (Ratios & Proportions) 7th Grade Word Problems (Fractions & Percent)

Worksheets And Questions For Grade 1 Singapore Math (Primary 1)

Number Bonds Numbers To 10 Making number bonds with cubes, Learn Number Bonds in Song, What Makes 10? Number Bonds - Addition within 10 Number Bonds - Subtraction within 10

Fact Families or Family of Number Sentences Making A Family Of Number Sentences, Fact Families.

Place Value: Numbers to 20 Place Value: Give the digit in the tens or ones place Place Value: Give the place value of the digit

Addition using number bonds Adding by Making 10, Adding Tens and Ones, Add a Two-Digit Number and One-Digit Number, Adding by grouping tens. Worksheets To Practice Addition 2-digit number + 1-digit number (no regrouping) 2-digit number + 1-digit number (with regrouping)

Subtraction using number bonds Subtract Ones, Subtract a One-Digit Number from a Two-Digit Number, Subtract Tens, Subtract Tens and Ones. Worksheets To Practice Subtraction 2-digit number − 1-digit number (no regrouping) 2-digit number − 1-digit number (with regrouping)

Adding and Subtracting Multiples of 10 Adding a Multiple of 10 to a Two-Digit Number, Subtract a Multiple of 10 from a Two-Digit Number. Word Problems for addition and subtraction

Worksheets & Questions For Grade 2 Singapore Math (Primary 2)

Numbers: Tens & Ones, Two-Digit Number Words, Place Values Worksheets to practice 2-digit number words Mental Math Strategies Add/Subtract Ones Add subtract tens

Worksheets & Questions For Grade 3 Singapore Math (Primary 3)

Place Values Read & write up to 10,000, Relate each 4-digit number to its place value, Compare & order numbers within 10,000, Number patterns with place values. Worksheets To Practice Place Values Give the digit in the thousands, hundreds, tens or ones place Give the place value of a specified digit

Adding 4-digit numbers Subtracting 4-digit numbers Worksheets To Practice Addition 4 digit numbers + 2-digit numbers 4 digit numbers + 3-digit numbers 4 digit numbers + 4-digit numbers Worksheets To Practice Subtraction 4 digit numbers − 2-digit numbers 4 digit numbers − 3-digit numbers

Worksheets & Questions For Grade 4 Singapore Math (Primary 4)

Fractions Types of Fractions, Improper Fractions & Mixed Numbers, Simplifying Fractions & GCF, Comparing Unlike Fractions & LCM, Subtracting Related Fractions. Worksheets on Fractions Equivalent Fractions, Comparing Fractions, LCM, Adding & Subtracting Fractions. Shape & Area Which shape cannot tessellate? Areas of Figures,Decimals.

Worksheets & Questions For Grade 5 Singapore Math (Primary 5)

Whole Numbers Place Values of Whole Numbers, Writing Whole Numbers from Figures to Words, Writing Whole Numbers from Words to Figures or Numerals. Comparison & Approximation Comparison, Ordering & Patterns in Whole Numbers, Approximation & Estimation, Whole Numbers. Basic Operations Multiplying Whole Numbers by 10s, 100s & 1000s, Dividing Whole Numbers by 10s, 100s & 1000s, Operations on Whole Numbers, Order of Operations.

Add & Subtract Fractions Add fractions (adding unlike fractions), Subtract fractions (subtracting unlike fractions), Add mixed fractions or mixed numbers, Subtract mixed numbers or mixed fractions. Multiplying & Dividing Fractions Multiplying fractions, Multiplying a mixed number (mixed fraction) & a whole number, Dividing a proper fraction by a whole number, Concept of fraction as division.

Decimals Fractions & decimals, Multiplying Decimals by 10s, 100s & 1000s, Dividing Decimal Numbers by 10s, 100s & 1000s, Rounding off Decimals, Approximation & Estimation of Decimals. Multiply Decimals by 10s, 100s & 1000s Divide Decimals by 10s, 100s & 1000s

Percent Introduction to Percent, Percent & Fraction, Percent & Decimal.

Geometry Angles, angles on a straight line Angles at a point Vertically opposite angles Isosceles triangle, equilateral triangle & right-angled triangle Sum of angles of a triangle Drawing different types of triangle Find unknown angles in a four-sided figure Drawing parallelograms, rhombus & trapeziums

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• Benefits to Participating Communities
• Participating School Districts
• Evaluations and Results
• Recognition Accorded
• National Advisory Committee
• Establishing New Institutes
• Topical Index of Curriculum Units
• View Topical Index of Curriculum Units
• Search Curricular Resources
• View Volumes of Curriculum Units from National Seminars
• Find Curriculum Units Written in Seminars Led by Yale Faculty
• Find Curriculum Units Written by Teachers in National Seminars
• Browse Curriculum Units Developed in Teachers Institutes
• On Common Ground
• Reports and Evaluations
• Articles and Essays
• Documentation
• Video Programs

Have a suggestion to improve this page?

To leave a general comment about our Web site, please click here

Share this page with your network.

Understanding Problems: Using Bar Models with Common Core Taxonomies

Introduction and rationale.

Next year I will teach third grade. This is a change from teaching fourth grade, where I have spent most of my teaching career up to now. Since I am switching grade levels, I recently reviewed Virginia’s standards for third grade mathematics. I was not surprised to see that the importance of problem solving is emphasized, considering that problem solving is always the most difficult aspect of the math curriculum to teach. I believe that many factors combine to create the difficulty: the nuances of each problem, the reading comprehension component, the application of skills, and the need for deeper understanding of computational skills. These aspects correspond roughly to Polya’s steps 1, 2, and 3. 1 In addition to the skills needed to understand and solve a problem, students need to have perseverance to bring it all together.

The Mathematics Standards of Learning for Virginia Public Schools 2 state: “Problem solving has been integrated throughout the six content strands. The development of problem solving skills should be a major goal of the mathematics program at every grade level. Instruction in the process of problem solving will need to be integrated early and continuously into each student’s mathematics education. Students must be helped to develop a wide range of skills and strategies for solving a variety of problem types.”

However, despite the emphasis placed on problem solving, there is little guidance or training on how to do that. In fact, as I read through the specific standards, one of the few utterances about problem solving that I found says the students will, “create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor 5 or less.” The standards do not mention any strategies or methods to use to solve problems.

When I go through the pacing guide provided by the school district, it skips around the textbook and provides random websites, some of which no longer exist, for additional practice. If a lesson is not directly tied to the standard, it is excluded. Fortunately for my students, I choose to follow the book more sequentially and intertwine Singapore math strategies, along with knowledge I have gained from working with Roger Howe through the Yale National Initiative.

Another issue that is promoted widely throughout resources and my school district is the strategy of key words to solve problems. By focusing on key words, children tend to spot the key word, then they choose what they deem to be the appropriate operation based solely on a word or two in the problem. Then they perform the “matching” operation on the numbers given in the problem. The key word strategy is limited, since a word problem with the word more may require addition or subtraction or, later in the curriculum, multiplication or division; and a word problem with the word less may require addition or subtraction depending on the given scenario. In order for our students to become more comfortable with problem solving, they need to comprehend the action and relationships described in the problem instead of relying on the key word strategy. To reiterate, the standards say, “The development of problem solving skills should be a major goal of the mathematics program at every grade level.” For this reason, I believe our students deserve better. Teaching the key word strategy to children is a disservice, especially given the importance of problem solving as stated in the Virginia State standards.

In order to address the issues listed above, I am creating a curriculum unit that focuses on problem solving techniques. I wrote a curriculum unit for fourth grade in 2007, titled Dr. Word Problem: Solving Word Problems with the Four Basic Operations of Mathematics Using Singapore Bar Models . 3 I do not want to duplicate that unit. This unit will address some of what I consider to be the best problem-solving strategies. I will briefly touch on Singapore bar models, but if you are interested in learning more about them, my 2007 unit is listed in the resources, and includes its own list of resources.

The crux of this unit is understanding the Common Core taxonomy of problems, 4 while infusing Polya’s steps, 5 and aspects of the Singapore model method. 6 I include a collection of word problems that identify the 14 types of one-step addition and subtraction problems and the nine one-step multiplication and division situations. The curriculum unit will include Polya’s four-steps as he is still considered the “guru” of problem solving for his work from 1945. 7 It will also include some steps from Singapore that are likely based on Polya’s four steps, as they seem to work hand in hand.  

Polya’s Method

George Polya was a mathematician from Hungary, who focused on problem solving. In his most prized publication, How to Solve It was published in 1945, Polya identifies four principles of problem solving.

Polya’s First Principle: Understand the problem

Polya’s Second Principle: Devise a plan

Polya’s Third Principle: Carry out the plan

Polya’s Fourth Principle: Look Back

The first principle is the most important for elementary students. The students should perform quite well with relatively simple word problems to which they are exposed if they can understand what is happening in the word problem.  

A Brief History of Singapore Math

In 1965 Singapore became an independent Republic. Recognizing that there are no resources in Singapore except the people, this young nation focused on education as a means to transform its economy. In a report authored by Dr. Goh Keng Swee, the Ministry of Education Study Team identified weaknesses in Singapore’s educational system. The findings led to the introduction of a New Education System (NES) in 1979. The Curriculum Development Institute of Singapore (CDIS) was established in 1980 and charged with creating a new math curriculum. In 1981, the first primary mathematics curriculum was introduced based on the concrete-pictorial-abstract approach. By 1983, the ‘model method’ 8 was introduced in primary 5 and 6 to address difficulties students had with word problems. Today the model method is first introduced to students in primary 1. 9

Model Method

I have had much success with teaching my students how to use the model method. The training I have received regarding the Singapore model method teaches children to pull out and label the facts or the quantities from the problem. Then students write out the question, draw a model, and the final step is to refer back to the question and write the answer as a sentence that answers the question. The last step is not only helpful to make sure the students answered the question asked, but also because it essentially forces them to label the units. To reiterate, the steps I have my students follow are:

• Pull out and label the facts (quantities).
• Write the question.
• Draw a model to show the relationship between the quantities in the problem.
• Reread the question and write the answer as a sentence.

I have found that following these steps helps my students succeed. In my experience, it allows the students to focus more on the numbers, thus reducing the confusion the students face when they are mixed in with a bunch of words.

Because of my interest in and success with this method, I conducted further research into the history of the model method as well as the pros and cons of the technique, and the importance of identifying the unit to which the numbers in the problem refer. 10 It is informative and provides more insight into the technique.

The model method is a heuristic, or a practical method, used to solve whole number word problems representing part-whole and comparison problems. A before-after concept is used with both part-whole and comparison problems to solve more complex structures. The before-after concept involves drawing two bar model representations to represent different stages in the word problem. The model method allows students to solve higher level problems without the use of algebra. Additionally, the model method focuses on representation, which is the key to solving word problems.

According to Ng and Lee, 11 the model method can be broken into three phases. The first phase is the Text Phase 12 , in which children read the problem that is presented in text form. The second phase is the Structural Phase, 13 where the students transform the text into a model. The third phase is the Procedural-Symbolic Phase 14 .  In the final phase students have to use the model and develop the mathematical steps to solve it. Ng and Lee suggest that since primary students do not yet know how to work with equations, they must use the unitary method. 15 The unitary method is a technique where students undo operations to find the value of one unit. Typically, that unit can be used to figure out other chunks or pieces of the model, which lead to a solution to the problem. This strategy requires the students to develop arithmetic equations to stand for the unknown units, which is essentially what students do when solving with bar models. Due to the success of the Singapore math techniques and the model method, the curriculum has become more widely used across the world, and is popular in the United States.

Pros of the Model Method

There are many benefits to teaching the Singapore model method. Typically, students tend to see the numbers in a word problem and do the first calculation that pops into their heads. The model method helps teach students to slow down, read the problem several times, and think about what is happening. Once a student has gone through these steps, a model can be drawn to represent the situation. One could say, that it is a device that enforces Polya’s four step method. I can attest to this from my own experience as I learned how to use the model method to solve word problems. I find myself reading the problem over slowly several times until I understand the problem, which is Polya’s first step. Then, I extrapolate the key information that is both known and unknown, and restate the question in order to devise a plan as stated in Polya’s second step. In this case, the plan is to draw a picture, in particular, a bar model. Then, I carry out the plan (step three) and figure out the answer. Following Polya’s fourth step, I check over my work to make sure it makes sense. According to Englard, the model method “Puts the focus back on the relationships and actions presented in the problem and helps students choose both the operations and the sequence of steps that are needed to solve the problem.” 16

The steps required to understand and draw a bar model is the crux of the model method. Ng and Lee 17 refer to a number of studies that found that visual and concrete representations improve performance in solving word problems. “The model-method affords higher ability children without access to letter symbolic algebra a means to represent and solve algebraic word problems.” 18 In one of the studies conducted by Ng and Lee, the teachers reported that because students represent the problem visually, it affords teachers the opportunity to inquire about difficulties students have with the representation. Another advantage of the model method is that it is not an “all or nothing process.” The findings agree with other research that reports that children tend to make their errors in the representation of the model. The Singapore model method has become a popular math instruction method because it is proven to enhance problem solving skills.

Cons of the Model Method

Yan Kow Cheong with Math Plus Consultancy conducted a study of the model method. The difficulties noted pertain more to problems drawing the models. Cheong noted three main problems: 1) difficulty of an “accurate diagram,” 2) division in a block diagram, and 3) inappropriate use of the model method. 19

It can be difficult for students to draw models accurately. While the models do not have to be drawn to scale, the model does need to accurately represent the problem. The division of the blocks is problematic particularly when a bar model requires additional partitioning. Another problem is that some curriculum books are overusing the model method when it is not appropriate. Cheong explains that some writers of curriculum books, while pushing the use of the model approach, are using the method when it is not appropriate.

Difficulties with algebra

Solving word problems with algebra is particularly problematic due to:

1) understanding the meaning of letters used in symbolic algebra,

2) translating natural language into equations,

3) understanding the semantic structure of word problems, in particular the nature of relationships between quantities and how they are linked, and

4) using text-based semantic cues in the construction of equations.” 20

Singapore students who have been taught the model method have exhibited challenges transitioning to algebra. “Studies (e.g. Ng et al. ) 21 have shown that poor bridging of students from the use of bar diagrams to the use of letter-symbolic algebraic methods can hinder their learning of algebra.” 22 The bright students don’t seem to have problems transitioning to algebra, but others tend to hold onto the bar model heuristic. A software tool called ALGEBAR 23 was designed in an effort to provide better bridging between the two subjects. Researchers conducted several studies to develop not only software, but a larger instructional package to address the algebra difficulties. The research determined that secondary problem solving requires mixed schemas. Students who used the bar models relied on these primary school schemas and forward calculations. Basically, prior knowledge influences new learning, and in this case, hinders it. According to this study, “students need to be taught the explicit structural homomorphism between bar model representation and algebraic equations.” 24 Students tend to want to calculate instead of manipulating the letter-symbol algebraic equations. Teachers should provide scaffolding by using models followed by weaning once the students gain comfort with equations. Eventually, more difficult problems that can only be solved with algebra should be introduced, so the students will realize the importance of letter-symbol algebra and link it to their prior knowledge. While the ALGEBAR is not a part of my curriculum unit, this article provided insight into how the model method hinders students’ algebra acquisition.

Whole Group Discussion

A strategy I will consciously infuse into my math block is more whole group discussion. I plan to use Math Talks throughout the year, so my students will use content specific vocabulary to explain their mathematical thinking. The other way I will employ whole group discussion is by affording time several times a week to discuss solutions and misconceptions about word problems. By sharing solutions and errors, the students will see that there are many ways to solve a single problem and that they can in fact learn from mistakes, even if they are not their own. The goal is that over time, students will not only become more comfortable with the idea of conversing about math, but will also learn from each other’s brilliance as well as shortfalls.

Taxonomy of Word Problems

The Common Core uses a chart giving a taxonomy of one step addition and subtraction situations. 25 Three main types are identified: change , comparison, and part-part-whole . The change and comparison are then split into two main subtypes: change plus and change minus, and more and less, respectively. Each of these types is further subdivided into three more categories based on the unknown. For the change problems, these categories are: result unknown, change unknown, start unknown. For the comparison problems, the categories are: difference unknown, bi gger unknown , and smaller unknown . The third main type, the part-part-whole, differs because there are only two subtypes: total unknown (whole unknown) or addend unknown (part unknown). There are interchangeable names for the various types of problems because the Common Core standards use names in the chart, but in literature other names are used to describe the problem types. I refer to them with the various names to build teacher background knowledge and hopefully to avoid confusion. These types will be discussed below with examples. I do not plan to have the students name the types, but it is really important to expose the students to all of the different kinds of problems.

As you explore these word problems, the natural connection between addition and subtraction will become more evident. For example, you will see that there are equations in which addition represents the problem, but subtraction is required to solve it.

As the different types of problems are introduced, the same numbers and situation will be explored. The numbers chosen for the initial explanation of the problem types will be small whole numbers. This is done purposefully, because the focus at this point is on introducing the problem types and evoking the similarities and differences.

Addition and Subtraction - Change

“Add to” or “Change plus”

For this category, the problem could have a result unknown, a change unknown , or a start unknown.

Eight birds are sitting on the fence. Three more land on the fence. How many are on the fence now? The bar diagram for this problem is in Figure 1.

This is an add to (change plus)/ result unknown since there were eight birds on the fence and a positive change happened indicating addition. The total number of birds on the fence is unknown, therefore it is a result unknown . The equation to solve the problem is 8+3=∎.

The next example is an add to (change plus)/change unknown. Eight birds were sitting on the fence. Some more landed on the fence. There are now 11 birds on the fence. How many birds landed on the fence? The diagram for this is given in Figure 2.

In this situation, the number of birds originally on the fence is known. Then some more birds join them, but the problem does not state how many more came. The result is 11 birds on the fence. The equation is now 8+∎=11. While the equation shows addition, this problem is solved by subtraction 8+∎=11.  If students were using a key word strategy, they would see the word more , thus students may be inclined to add eleven and eight, which does not answer the question.

The third type is add to (change plus)/start unknown.

Some birds are on the fence. Three more land on the fence. There are now 11 on the fence. How many were on the fence in the beginning? Figure 3 shows the bar model for this problem.

It would be expressed as ∎+3=11. The initial number of birds on the fence is unknown. The equation shows addition, but again, subtraction is required to solve for the answer; 11-3=∎. Once again, using the key word method, students would mistakenly be inclined to add eleven plus three since the key word more is used.

“Take from” or “Change minus”

These are also “add to” problems, but now the change is being “taken from.” There are the same three types: result unknown, change unknown, and start unknown.

The first problem is a Take from/result unknown .

Six squirrels were in a tree. Two ran away. How many were left in the tree? The equation is 6-2=∎ ,and it would be solved with subtraction. The bar model is shown in Figure 4.

The second problem of this kind is a Take from/change unknown .

Six squirrels were in a tree. Some ran away. There were four left in the tree. How many ran away? Mathematically, the equation is 6-∎=4, and the solution is ascertained by subtracting 6-4=2. The diagram for this is given in Figure 5.

The last one in this series is a Take from/ start unknown .

Some squirrels were in a tree. Two ran away. There were four left. How many were in the tree at the start? The bar model for this problem is shown in Figure 6.

The equation is ∎-2=4 , but the solution is found by computing 4+2=6.  Once again, the key word method would be problematic. The problem says left , which typically means to subtract, but in fact addition is required.

Addition and Subtraction - “Put together” or “Part-part-whole”

For these, it is either an unknown part or unknown addend or an unknown whole or unknown total.

There are six green apples and four red apples are in a bowl. How many apples are in bowl?

The number sentence is 6+4=∎, and the answer is 10. The diagram for this problem is given in Figure 7.

An example of an unknown part or unknown addend is:

There are 10 apples in the bowl. There are six green apples and the rest are red apples. How many apples are red? Figure 8 shows the bar model for this problem.

The equation, 6+∎=10, is used to represent the problem, but to compute the answer students need to compute 10-6=4.

Addition and Subtraction - Compare

The compare problems are probably the trickiest of the addition and subtraction types. There are two of each kind: difference unknown , bigger unknown , and smaller unknown , for a total of six. Part of the confusion stems from the interchangeable vocabulary used to describe these types.

Difference unknown/more

Jaquan has six apples. Devin has two apples. How many more apples does Jaquan have than Devin? The model is shown in Figure 9.

It is a difference unknown, as the answer to the subtraction problem is unknown. It falls into the more category because the question asks, “ How much more?” The number sentence 2+∎=6 represents this problem. However, the operation needed solve the problem is 6-2=∎.

Difference unknown/fewer (less)

Jaquan has six apples. Devin has two apples. How many fewer does Devin have?

The sentence 6-2=∎ will provide the solution. Figure 10 models this problem.

The two problems above sound quite different, but are answered with the same computation.

Bigger unknown/more

Jaquan has 4 more apples than Devin. Devin has 2 apples. How many apples does Jaquan have?

The equation 2+4=∎, leads to the correct answer of 6 apples. The bar model to represent this problem is shown in Figure 11.

Bigger unknown/fewer (less)

Devin has 4 fewer apples than Jaquan. Devin has 2 apples. How many apples does Jaquan have?

In order to determine the number of apples Jaquan has, use the equation 2+4=∎. Figure 12 provides the model for this problem.

The two problems above, again, sound quite different, but are answered with the same computation.

Smaller unknown/more

Jaquan has 4 more apples than Devin. Jaquan has 6 apples. How many apples does Devin have? The statement ∎+4=6 represents this scenario, but the subtraction sentence 6-4=∎ is needed to solve this problem. Once again, the word more that indicates addition when using the key word strategy would lead students astray. The model in Figure 13 represents this problem.

Smaller unknown/fewer (less)

Devin has 4 fewer apples than Jaquan. Jaquan has 6 apples. How many apples does Devin have? 6-4=∎ will solve this problem. Figure 14 shows the bar model for this problem.

The two comparison problems above are answered with the same computation, and sound quite different.

As with addition/subtraction problems, there are designated problem types for multiplication and division with three main categories: equal groups, comparison , and array/area . Just as the main types of addition/subtraction problems addressed different important contexts where addition and subtraction are used, the categories of multiplication/division problems point to the main interpretations or applications of these operations. The equal groups and comparison ones are closely related. The number of groups is analogous to the comparison factor . In fact, when a collection is made out of a number of equal groups, the comparison factor between the big collection and one of the groups is exactly the number of groups. Another similarity between the compare and the comparison problems are that they both can be represented through linear measurement. The equal groups and the comparison problems have three subcategories: unknown product, groups size unknown, and number of groups unknown.  The arrays/area problems are different because they represent problems in two-dimensions. The Singapore bar models are a linear representation of a problem, and would not be an effective strategy for array/area models. As you read these examples, notice how multiplication equations are often solved with division and vice versa. I will now explain each type as I did for the addition and subtraction ones.

Multiplication/division – equal groups

Equal groups/unknown product

At the toy store, cars come in packs of six. If Jose buys four packs, how many toy cars will he buy in total? 6×4=∎ is the equation and the product is 24. The representation is shown in Figure 15.

Equal groups/group size unknown

At the toy store, Jose buys 24 cars. Jose buys four packs. How many are in each pack?

In this situation, 4×∎=24 the number of groups (packs) and the product is known, but the number in each group or the groups size is unknown. The equation sets up as a multiplication problem, but it uses division 24÷4=6 to find the solution. The bar model in Figure 16 shows this problem.

Equal groups/number of groups unknown

This next problem type is about equal groups. It is like the previous one but instead of group size, the number of groups is unknown.

At the toy store, Jose buys 24 cars. There are six in each pack. How many packs does Jose buy? The equation 6×∎=24 represents the scenario. The number in each group is known as is the product or total that Jose bought. The unknown is the number of groups or how many packs Jose buys. Once again division is used: the equation 24÷6=4 determines that the answer is four groups. The bar model in Figure 17 shows this problem. Notice the ellipses, which are used when the number of groups is unknown or when there are a large number of groups.

Multiplication/division – arrays/area

These problems use situations with objects arranged into rows or columns, representing an array, or they use measurement to show area. These are essentially equal groups problems, with the rows being the groups, and the columns being the number of groups. The point of making them a distinct category is to connect with the area model for multiplication. The arrays and area problems do not align well with Singapore bar models; therefore, I did not include images of bar models in this section.

Arrays/area – unknown product

Some chairs are arranged in the classroom. There are three rows of seven chairs. How many chairs are in there? The multiplication sentence 3×7=∎ corresponds to this problem, and the answer is 21 chairs.

Arrays/area – group size unknown

Twenty-one chairs are arranged into three equal rows. How many chairs are in each row? 3×∎=21 depicts this situation, but division is required to determine the group size of each row. So, 21÷3=7 results in the solution to this problem. In this problem, the number of equal groups is known, but the group size is unknown.

Arrays/area – number of groups unknown

Twenty-one chairs are arranged into equal rows. There are seven chairs in each row. How many rows will there be?  The number sentence 7×∎=21 depicts this problem, but students must divide 21÷7=3 to ascertain the answer. In this similar situation, the number of chairs in each group is known, but the number of groups or rows is unknown.

Multiplication/division – comparison

The multiplication comparisons are also used to express measurement problems. An example and explanation of one with and without measurement is listed below.

Compare/unknown product

A pack of gummy bears cost $ 2 and a sandwich costs three times as much. How much does the sandwich cost? The equation $ 2×3=∎ denotes the scenario, and multiplication is used to determine that the cost of the sandwich is $ 6. The bar model in Figure 18 represents this problem.

Jamie wants to measure the length of her desk using a large paper clip. She lays 24 paper clips end to end. Each paper clip is two inches long. What is the length of her desk? This would be represented mathematically as 24×2=∎. Figure 19 models this problem.

Compare/smaller quantity unknown

A sandwich costs $6. It costs three times as much as gummy bears. How much do the gummy bears cost? Therefore 3 × ∎ = $ 6 , but the operation of division $ 6 ÷ 3 = $ 2 is necessary to find the answer. The smaller quantity, or in this case, the price of the gummy bears is unknown. Three groups of $2 equals $6. The bar model is shown in Figure 20.

Compare/ Comparison factor unknown

A sandwich costs $6 and gummy bears cost $2. How many times as much does the sandwich cost? The statement $ 2 × ∎ = $ 6  represents the situation, but the division sentence $ 6 ÷ $ 2 = 3 is needed to determine the comparison factor. The bar model for this problem is shown in Figure 21.

Multi-step word problems

All of the above-mentioned types of problems are one-step problems: they require only a single computation to arrive at an answer. One-step problems can be combined to make problems with several steps – two, three, or even more. One could say, they are the nuts and bolts that make up multi-step problems. I expect that, exposing my students to the component parts and developing a level of comfort with the various kinds will provide a strong foundation for them to be more successful with multi-step problems. Now, let’s look at a few examples of multi-step problems.

There are 37 children in the swimming pool. There are nine fewer adults than children in the pool. How many adults and children are in the pool? One way to solve this problem is to think 37-9=∎ to determine the number of adults in the pool. This first part is an addition/subtraction comparison, which will guide us to the number of adults in the pool. If 37-9=28, then there are 28 adults in the pool. The second step is to combine the number of adults and children with the equation 37+28=65. The second step is a put together or part-part-whole with the total unknown. As you can see, this two-step problem is comprised of situations that have already been discussed. Figure 22 shows the model for the first step in this problem.

37-9=28 adults, then a second bar model would represent the second step. The model below represents the second step which is an addition/subtraction part-part-whole problem with the whole unknown. The second step is modeled in figure 23.

Let’s look at one more example. Five children are on the playground. Then three times as many join them. How many children are on the playground now? The first step is multiplication/division comparison with the result unknown. This step is solved by calculating 5×3=∎. So, 15 children joined them. The second part is a change plus/result unknown which would use the addition statement 15+5=20 to figure out the result. Figure 24 shows both steps using a single bar model.

The one-step addition/subtraction and multiplication/division problems can be combined into about 400 types of two-step problems. It would be challenging to expose your students to all the different combinations of two-step problems. It would be impractical to teach all the combinations of three-step problems, as there are about 8,000 variations. Thus, the strategy of introducing students to the 23 parts that compose all multi-step problems is important to lay a strong foundation and should be taught with fidelity. An important takeaway, as demonstrated through the examples of word problems, is that inverse relationships between operations are not discrete. Therefore, addition and subtraction should be dealt with together, and likewise and multiplication and division should be dealt with at the same time.

The Virginia Standards of Learning state that the problem-solving process should be integrated early and continuously. So, I plan to work through the Common Core taxonomy of problem types right from the start of the school year. I plan to spend about 15 minutes of the daily math period on problem solving, introducing the 23 types of problems.

I will slowly introduce the types (i.e. Change Plus) one subcategory (i.e. result unknown, change unknown, and start unknown) at a time. I anticipate using the I do, we do, you do approach for each subcategory. So, the teacher will model, students will do one with me, and then students will do one alone. After a type has been fully introduced, I will allow time for a mixed review and students will engage in a Math Talk so students can share their solutions and misconceptions.

After students have worked with all 23 types, the focus will shift to multi-step problems, and will continue throughout the year. Below is the schedule I plan to follow beginning the second week of school.

Day 1 – Change Plus +/- result unknown

Day 2 – Change Plus +/- change unknown

Day 3 – Change Plus +/- start unknown

Day 4 – Mixed Change +/- plus problems and Math Talk

Day 5 – Change Minus +/- result unknown

Day 6 – Change Minus +/- change unknown

Day 7 – Change Minus +/- start unknown

Day 8 – Mixed Change Minus +/- problems and Math Talk

Day 9 – Mixed Change Plus +/-  and Change Minus +/- problems

Day 10 – Part-Part-Whole +/- whole unknown

Day 11 – Part-Part-Whole +/- part unknown

Day 12 – Mixed Part-Part-Whole +/- practice and Math Talk

Day 13 – Mixed Change Plus, Change Minus, & Part-Part-Whole +/- practice and Math Talk

Day 14 – Compare Difference Unknown +/- more

Day 15 – Compare Difference Unknown +/- less

Day 16 – Compare Bigger Unknown +/- more

Day 17 – Compare Bigger Unknown +/- less

Day 18 – Compare Smaller Unknown +/-  more

Day 19 – Compare Smaller Unknown +/- less

Day 20 – Mixed Compare Practice +/- and Math Talk

Day 21 – Mixed Change +/-, Part-Part-Whole +/- , Compare Practice +/- and Math Talk

Day 22 – Equal Groups ×/÷  – Product Unknown

Day 23 – Equal Groups ×/÷ – Group Size Unknown

Day 24 – Equal Groups ×/÷  – Number of Groups Unknown

Day 25 – Mixed Equal Groups ×/÷ Practice and Math Talk

Day 26 – Mixed Review Addition/Subtraction Change, Part-Part-Whole, Compare & Multiplication/Division Equal Groups ×/÷  practice and Math Talk

Day 27 – Area/Arrays ×/÷  Product Unknown

Day 28 – Areas/Arrays ×/÷  Group Size Unknown

Day 29 – Areas/Arrays ×/÷  Number of Groups Unknown

Day 30 - Areas/Arrays ×/÷  Mixed practice and Math Talk

Day 31 - Mixed Review Addition/Subtraction Change, Part-Part-Whole, Compare & Multiplication/Division Equal Groups and Areas/Arrays practice and Math Talk

Day 32 – Compare ×/÷  Unknown Product

Day 33 – Compare ×/÷  Smaller Quantity Unknown

Day 34 – Compare ×/÷  Comparison Factor Unknown

Day 35 -  Mixed Compare ×/÷  practice and Math Talk

Day 36 – Mixed Review Addition/Subtraction Change, Part-Part-Whole, Compare & Multiplication/Division Equal Groups, Areas/Arrays, Compare practice and Math Talk

Day 37 -  Mixed Review Addition/Subtraction Change, Part-Part-Whole, Compare & Multiplication/Division Equal Groups, Areas/Arrays, Compare practice and Math Talk

Day 38 - Multi-step Problems

Day 39 - Multi-step Problems

Day 40 – Multi-step Problems and Math Talk

Day 41 – Multi-step Problems and Math Talk

Day 42 - Multi-step Problems and Math Talk

Day 43 - Multi-step Problems and Math Talk

Day 44 - Multi-step Problems (ongoing throughout the year) and Math Talk

Day 45 – Problem Solving Assessment

I am selecting four activities from the above schedule to highlight and flesh out in more detail. I have selected Day 1, Day 4, Day 27, and Day 40 purposefully. Day 1 will introduce how I plan to go through each type of problem. Day 4 provides an example of the end of a type of problem review and lays out the format for the Math Talk. Day 27 is the first day of area/array problems and since this type of problem does not lend itself to bar models, it is important to lay out an approach. Finally, I chose Day 40 to share a Math Talk from the multi-step section. The problems will initially come from the collection of problems, and I will categorize and make up more as needed. I also will likely utilize some problem sets from curriculum units developed in the Yale National Initiative ® seminars with Roger Howe in 2015, Problem Solving with the Common Core, and 2017, From Arithmetic to Algebra: Variables, Word Problems, Fractions, and Rules.

Day 1 – I plan to kick off the unit by letting my students know that we will focus on problem solving this year, and will spend about 15 minutes each day working on problem solving strategies. We will also learn to solve many word problems using Singapore bar models because Singapore is ranked relatively high in math in the world. I will show them where Singapore is on a map.

Then I will introduce a Change Plus problem with a result unknown. I will not categorize the problem type, but I will provide three examples of a change plus result unknown problem. The first one I will model how to read the problem carefully, how to pull the facts out, how to write the question, how to draw a bar model, and how to go back to the question to write the answer in a statement. Then we will reflect as a class if the answer seems reasonable and makes sense.

Next, we will do another Change Plus problem with the result unknown. This time, the students will help me. I will ask them what the facts are. As they share a fact, I will record it and project it for the class to see. Once the facts are pulled out, a student will tell me the question to write down. Next the students will guide me to draw a bar model, solve the problem, and write the answer as a statement. I will ask students to share their thoughts on the reasonableness of the answer.

With the third problem, again a Change Plus result unknown, students will solve it independently following the steps that were modeled with the previous two problems.

Day 4 – For the mixed review, I plan to use one of each type of Change Plus problems. Students will solve three problems on a handout (using the steps learned in class.) Once students have completed the problems, we will share solutions, and students will have the opportunity to share different solutions or bar models. The Math Talk will begin organically as students share solutions, but I will work to guide students to understand the importance of providing a safe environment for sharing both correct and incorrect solutions. I also will stress the importance of learning from mistakes, yours and others, and how we can all benefit from talking about and analyzing misconceptions.

Day 27 – This is the first day area/array problems are addressed. Since these problems do not lend themselves to a bar model, I plan to point this out to students so they understand that a bar model is a linear representation and an array or area problem is two-dimensional. I intend to have students follow the same procedure as explained above, but instead of a bar model, students will draw a picture of the array or an area model using a rectangle.

Day 40 – Now that all of the problem types have been taught, students will now tackle two-step problems. Students should know that these are two-step problems, but that each step is similar to problems they have already solved. I anticipate these problems will lend themselves to a more robust class discussion as students have various solutions, particularly regarding the order in which the two steps are solved. The drawings may include two distinct bar models as shown in the multi-step problems previously described.

Sample Collection of Problems 

Add to/result unknown - very basic to introduce third graders to bar models

1) Eight birds were sitting on the fence. Three more landed on the fence. How many are on the fence now?

Add to/change unknown

2) Eight birds were sitting on the fence. Some more landed on the fence. There are now 11 birds on the fence. How many birds landed on the fence?

Add to/start unknown

3) Some birds were on the fence. Three more landed on the fence. There are now 11 birds on the fence. How many birds were on the fence in the beginning?

Add to/result unknown – using money

4) Josie had $17 and her grandma gave her $25 for her birthday. How much money does she have now?

Add to/ change unknown

5) Josie had $17. Her grandma gave her some money for her birthday. She now has $42. How much money did her grandma give her?

Add to /start unknown

6) Josie had some money. Her grandma gave her $25 for her birthday. She now has $42. How much money did Josie have at the start?

Add to/result unknown – three addends

7) If 234 people attend a concert on Thursday night, 367 attend on Friday night, and 329 people attend on Saturday night. How many total people attended the concert?

Add to/ change unknown – three addends

8) 234 people attend on Thursday night, and 367 attend on Friday night. A total of 930 people attended on Thursday, Friday, and Saturday. How many people attended on Saturday?

Add to/ start unknown

9) After buying 62 stamps, Mr. Jones now has 418 stamps. How many did he have at first?

Take from, Change unknown

10) Mr. Sims had 245 stamps. Then Mr. Jones gave him some. He now has 312. How many did Mr. Jones give him? (Add to /change unknown)

Put together/total unknown

11) What is the total length of the sides (perimeter) of a triangle if one side is 23 inches, another is 19 inches, and the third side is 32 inches?

Compare less, larger unknown

12) Paul is 21 years old. He is 23 years younger than his mother. How old is his mother?

Compare more, bigger unknown

13) There are 342 trucks parked outside the football stadium. There are 147 more cars than trucks. How many cars are there?

Subtraction

Take from/result unknown - A really simple problem to introduce bar models

14) Six squirrels were in a tree. Two ran away. How many were left in the tree?

Take from/change unknown

15) Six squirrels were in a tree. Some ran away. There were four left in the tree. How many ran away?

Take from/ start unknown

16) Some squirrels were in a tree. Two ran away. There were four left. How many were in the tree at the start?

Put together/addend unknown or Part-Part-Whole/ part unknown

17) A total of 39 dogs and humans were at the dog park. If there were 22 dogs, how many humans were there? **

Put together/total unknown or Part-Part-Whole/ total unknown

18) There were six green apples and four red apples are in a bowl. How many apples are in bowl?

Put together/part unknown or Part-Part-Whole/ part unknown

19) There are 10 apples in a bowl. Six of the apples are red and the rest are green. How many are green?

Part-Part-Whole/ part unknown or Put together/addend unknown

20) There are 263 people watching a play. If 79 of them are children, how many are adults?

21) There were a total of 406 people at the symphony concert. There were 214 children and the rest were adults. How many were adults?

Part-Part-Whole/whole unknown

22) There are 402 boys and 369 girls watching a parade. How many children are watching the parade in all?

Compare/difference unknown/more

23) Sam has $28. Jaquan has $31. How much more money does Jaquan have than Sam?

Take from/Result Unknown

24) Ryan had $134. He spent $28 at the Sporting Goods Store. How much money does he have left?

Take from/result unknown

25) Twenty-two dogs were playing at the dog park. Three left with their owners. How many dogs are at the dog park now?

Take from/Start unknown

26) Ryan went to the Sporting Goods store with his money. Ryan spent $46 in the Sporting Goods Store. He had $78 left. How much money did he have at first?

27) Mia had $124. She purchased some spinners. She now has $88. How much did the spinners cost?

Multiplication

Equal groups/product unknown

28) At the toy store cars come in packs of six. If Jose buys four packs, how many toy cars will he buy in total?

Equal groups (measurement)/product unknown

29) Mrs. Bronto has 14 cans of Saurus Soup. If each can is three inches high, and she piles them one on top of another to make a Brontosaurus Soup Tower, how high will the tower be?

Equal groups/ product unknown

30) Jordan is having a birthday party. He wants to have a can of soda for all of his guests. If there are 18 people at the party, how many six-packs of soda will his mom have to buy, so everyone can have one can of soda?

Equal groups (measurement)/ group size unknown

31) Sami has Fruit by the Foot and it is 36 inches long. She cuts it into equal pieces so she and her three friends will each have a piece. How long will each piece of string be?

Equal groups (measurement)/ number of groups unknown

32) Mr. Davis, the art teacher, has a piece of yarn 56 inches long.  He cuts it into pieces that are seven inches long. How many pieces will he get?

Arrays/area, group size unknown

33) Ben draws a rectangle with an area of 24 square centimeters. If one side is eight centimeters long, how long is a side perpendicular to it?

Array/area, number of groups unknown

34) Ms. Carpenter cuts a rectangle out of fabric. It is 48 square inches. The length is eight inches. How long is the width?

Compare/group size unknown

35) Aidan has three times as much money as Ella. They have a total of $36. How much money does Ella have?

36) If Mrs. Pencil goes to the store to buy erasers for the class. There are 24 students in the class. Erasers are sold three in a pack. How many packs of erasers must she buy to have one for each student?

Arrays/area, product unknown

37) Naomi is making an array with two-sided counters. She puts seven in a row and makes six rows. How many two-sided counters are in her array?

38) There are three equal sections in the theater. Each section has eight rows with the same number of seats. There are 72 seats in each section. How many seats are in each row?

Arrays/area, size of group unknown

39) Mr. Rebmann is setting up chairs for a band concert. He needs 32 seats for the band members. He decides to put eight chairs in each row. How many rows does he need?

Compare (measurement)/product unknown

40) A Slinky is four inches long when in its box. How long will it be when it is stretched five times its length?

Compare (measurement)/smaller quantity unknown

41) Jennie has a jump rope. It is 48 inches long. This is six times the length of Sophia’s shoe. How long is Sophia’s shoe?

Compare (measurement)/comparative factor unknown

42) Shannon can spin her spinner on her finger for 42 seconds. Will can only spin his spinner for seven seconds. How many times longer can Shannon spin her spinner than Will?

43) Ebony has a collection of seashells. She has 32 seashells. This is four times as many as Shannon has. How many seashells does Shannon have?

44) In a parking lot, there are four times as many cars as buses. There are 356 cars. How many buses are there?

45) Justin has some dogs. He goes to the pet store and sees four times as many. There are eight dogs at the pet store. How many dogs does Justin have?

46) James buys packs of pencils for her classroom school supplies. She buys 192 pencils, which is eight times the number of students in her class. How many students are in her class?

Compare, smaller unknown and Put together/Part-part-whole, total/whole unknown

47) There are 37 children in the swimming pool. There are nine fewer adults than children in the pool. How many adults and children are in the pool?

Compare, bigger unknown and Put together/Part-part-whole total/whole unknown

48) Jaden has $37. If Nico has $6 more than Jaden, how much do Jaden and Nico have in all?

Change minus/Take from, result unknown and Change plus/Add to, result unknown

49) Jazmin has 47 stickers. She gives eight to Sammy. Then she gets 26 more for her birthday. How many stickers does she have now?

Compare, fewer unknown and Put together/Part-part-whole, total/whole unknown

50) Children are at a concert. There are 3,402 boys, and there are 987 fewer girls than boys. How many children are there in all?

Put-together/ Part-Part-whole, total/whole unknown and Compare, smaller unknown

51) At a show, there are 6,020 spectators - men, women and children. There are 3,860 men and 2,020 women. How many children are there?

Multiplication/division compare, unknown product and Put together/Part-part-whole, total/whole unknown

52) Joe has a stamp collection. He has 135 U.S. stamps, and three times as many foreign stamps. How many foreign stamps does he have? How many stamps does he have all together?

Change minus/take from, result unknown and Equal groups, unknown product

53) Haskell earns $2,395 per month. He spends $1,780 per month, and saves the rest. How much does he save in six months?

Bibliography

Bokhorst-Heng, W.D., M.D. Osborne, K. Lee, J. Albright, B. Comber, J. Dornbrack, H. K. Fai, A. Firkins, N.S. Fong, G. Forey, P.J. Gilmer, M. Hanrahan, C. Hart, J.G. Hedberg, M. Hoechsmann, S.L. Hoon, M. Ismail, B. Kamler, F. Khng, D. Kwek, K. Lee, L.M. Ling, T.A. Ling, L.T. Lioe, J. Ng, M.D. Osborne, K.D. Purohit, D. Sankey, L. Soong, A. Vongalis-Macrow, C.S. Walsh, J. Wolf, S. Wright, E.H. Wuan, A.S. Yin, W.K. Yong, and K.P. Yuk. Redesigning pedagogy: reflections on theory and praxis. Rotterdam The Netherlands: Sense Publishers, 2006.

The Model method: obstacle or bridge to learning symbolic algebra pages 227-242 was referenced in the Looi & Lim article and this is where the referenced study originated.

Cheong, Yan Kow. "The Model Method in Singapore."  The Mathematics Educator , 2002nd ser., 6, no. 2 (2002): 47-64. Accessed June 09, 2017. JSTOR.

This article speaks to the power of the model method as a technique to teach problem solving.

Englard, Lisa. "Raise the Bar on Problem Solving."  Teaching Children Mathematics 17, no. 3 (October 2010): 156-63. Accessed May 14, 2017. JSTOR.

This article is easy to read and reveals the results of teaching bar models to students.

Fan, Lianghuo, and Yan Zhu. "Representation of problem-solving procedures: A comparative look at China, Singapore, and US mathematics textbooks."  Educational Studies in Mathematics 66, no. 1 (2007): 61-75. Accessed June 09, 2017. doi:10.1007/s10649-006-9069-6.

This article compared problem solving in text books from three countries. It was not very helpful, but provided a little insight.

Fong, Ng Swee, and Kerry Lee. "Model Method: A Visual Tool to Support Algebra Word Problem Solving at the Primary Level."  Series on Mathematics Education Mathematics Education , 2009, 169-203. Accessed June 09, 2017. doi:10.1142/9789812833761_0008.

This article focuses on using the model method to solve algebra word problems. It addresses some strengths, but also some shortfalls.

Kaur, Berinderjeet. "Evolution of Singapore's school mathematics curriculum."  MERGA , July 2014, 24-36. Accessed June 9, 2017. JSTOR.

This report describes how the education in Singapore has evolved. The report was insightful.

Kaur, Berinderjeet. "The model method: A tool for representing and visualising relationships."  Conference Proceedings of ICMI Study 23: Primary mathematics study on whole numbers , June 3-7, 2015, 448-55. Accessed June 09, 2017. JSTOR.

This article provides an overview of the model method for primary students.

Looi, C.-K.,-S. Lim. “From bar diagrams to letter-symbolic algebra: a technology-enabled bridging.” Journal of Computer Assisted Learning 25.4 (2009): 358-74. Web. 5 June 2017. JSTOR. This article addresses the difficulty students in Singapore have moving from bar diagrams to algebra. The ALGEBAR computer technology helps to bridge the gap.

Melvin, George W. “Polya’s Problem Solving Techniques.” https://math.berkeley.edu/~gmelvin/polya.pdf., N.p. n.d. Web. 6 July 2017. This site provides a brief overview of Polya’s steps.

Ng, Swee Fong, and Kerry Lee. "The Model Method: Singapore Children's Tool for Representing and Solving Algebraic Word Problems."  Journal for Research in Mathematics Education 40, no. 3 (May 2009): 282-313. Accessed June 09, 2017. JSTOR.

This article examines the model method and emphasizes aspects to look for when teaching students the method.

Xin, Yan Ping, and Dake Zhang. "Exploring a Conceptual Model-Based Approach to Teaching Situated Word Problems."  The Journal of Educational Research 102, no. 6 (2009): 427-42. Accessed June 09, 2017. doi:10.3200/joer.102.6.427-442.

This article supports the use of the model method to teach students in grades 3 through 5.

Additional Resources for Teachers and Students

A., Van De Walle John. Elementary school mathematics: teaching developmentally . London: Longman, 1994.   An excellent resource for teaching all aspects of elementary math in a concrete way.

Bluman, Allan G. Math word problems demystified . New York: McGraw-Hill, 2011. This book is full of word problems at all levels as well as word problem strategies. The problems would need to be carefully selected for the appropriate grade level.

Chew, Terry. Singapore math challenge: grade 3 . Columbus, OH: Frank Schaffer Publications, 2013.   A wonderful challenging book to develop math thinking for students in grades 3-5 in the U.S.

Forsten, Char. Step-by-step model drawing: solving word problems the Singapore way . Peterborough, NH: Crystal Springs Books, 2010.   Another good source for word problems that are made for the model method.  

Primary mathematics . Singapur: Marshall Cavendish Education, 2003.   A source of word problems for bar modeling appropriate for high third graders or fourth grade students in the U.S.

Primary mathematics 2A . Singapore: Marshall Cavendish Education, 2006.   A good source of word problems that lend themselves to bar models. The level 2 books are appropriate for grade 3 in the U.S.

Primary mathematics 2B . Singapore: Marshall Cavendish Education, 2006.

Primary mathematics 3B . Singapore: Marshall Cavendish Education, 2007.   This is also a resource for high third graders or four grade students in the U.S.

Appendix A: Implementing District and National Standards

This curriculum unit is designed to provide a framework for teaching word problems focused on building students’ understanding of the word problem. It utilizes the taxonomy of situations from the Common Core standards, which the state has added to Virginia’s math standards of learning curriculum framework for 2016. The 2016 standards will be phased in during the 2017-18 school year and tested in 2019. This unit aligns to the new guidelines from the state and also provides another proven tool with the bar model.

Virginia’s Standards of Learning (2009)

3.2  The student will recognize and use the inverse relationships between addition/subtraction and multiplication/division to complete basic fact sentences. The student will use these relationships to solve problems.

3.4  The student will estimate solutions to and solve single-step and multistep problems involving the sum or difference of two whole numbers, each 9,999 or less, with or without regrouping.

3.6  The student will represent multiplication and division, using area, set, and number line models, and create and solve problems that involve multiplication of two whole numbers, one factor 99 or less and the second factor 5 or less.

The above standards are for 2009. This year the 2016 standards are being implemented. The end- of-the-year test will cover 2009 standards and will include field test items from the 2016 standards. 

Regarding problem solving, the only difference between 2009 and 2016 is that in 2016 students will solve problems with elapsed time. The standards are pretty vague. When I went to the Curriculum Framework document, I discovered charts with problem types. They are practically identical to the Common Core chart, with a few different names. These are new additions to the Virginia Standards.

Virginia’s Standards of Learning (2016)

3.3 The student will

b) create and solve single-step and multistep practical problems involving sums or differences of two whole numbers, each 9,999 or less

3 . 4 The student will

b) create and solve single-step practical problems that involve multiplication and division through 10 x 10;

d) solve single-step practical problems involving multiplication of whole numbers, where one factor is 99 or less and the second factor is 5 or less.

3.9 The student will

b) solve practical problems related to elapsed time in one-hour increments within a

12-hour period;

c) identify equivalent periods of time and solve practical problems related to equivalent periods of time.

Common Core Standards

CCSS.MATH.CONTENT.3.OA.A.3 Use multiplication and division within 100 to solve word problems in situations involving equal groups, arrays, and measurement quantities, e.g., by using drawings and equations with a symbol for the unknown number to represent the problem.

This standard relates directly to the taxonomy chart and the types of problems discussed in my curriculum unit.

CCSS.MATH.CONTENT.3.OA.D.8 Solve two-step word problems using the four operations. Represent these problems using equations with a letter standing for the unknown quantity. Assess the reasonableness of answers using mental computation and estimation strategies including rounding.

By learning all of the types of one step problems, students will combine them to solve two-step problems. By utilizing Polya’s steps, students will be taught how to check answers for reasonableness.

The following three standards relate to area and perimeter problems. A few are included in the collection of problems.

CCSS.MATH.CONTENT.3.MD.C.7.B Multiply side lengths to find areas of rectangles with whole-number side lengths in the context of solving real world and mathematical problems, and represent whole-number products as rectangular areas in mathematical reasoning.

CCSS.MATH.CONTENT.3.MD.C.7.D Recognize area as additive. Find areas of rectilinear figures by decomposing them into non-overlapping rectangles and adding the areas of the non-overlapping parts, applying this technique to solve real world problems.

CCSS.MATH.CONTENT.3.MD.D.8 Solve real world and mathematical problems involving perimeters of polygons, including finding the perimeter given the side lengths, finding an unknown side length, and exhibiting rectangles with the same perimeter and different areas or with the same area and different perimeters.

• G. W. Melvin, “Polya’s Problem Solving Techniques,” https://math.berkeley.edu/~gmelvin/polya.pdf.
• http://www.doe.virginia.gov/testing/sol/standards_docs/mathematics/index.shtml
• V. Schwarz, “Dr. Word Problem – Solving Word Problems with the Four Operations Using Singapore Bar Models,” The Yale National Initiative , last modified July 2007. http://teachers.yale.edu/curriculum/viewer/initiative_07.06.05_u
• Common Core State Standards Initiative, “Mathematics Glossary Table 1 & Table 2” http://www.corestandards.org/Math/Content/mathematics-glossary/Table-1/ http://www.corestandards.org/Math/Content/mathematics-glossary/Table-2/
• G.W. Melvin, “Polya’s Problem Solving Techniques,” https://math.berkeley.edu/~gmelvin/polya.pdf.
• B. Kaur, “The model Method: A tool for representing and visualizing relationships,” http://www.umac.mo/fed/ICMI23/doc/Proceedings ICMI STUDY 23 final.pdf
• B. Kaur, “Evolution of Singapore’s school mathematics curriculum,” Curriculum in Focus: Research Guided Practice 29 June to 3 July 2014.
• B. Kaur, “The model Method: A tool for representing and visualizing relationships,” 449. http://www.umac.mo/fed/ICMI23/doc/Proceedings ICMI STUDY 23 final.pdf
• S.F. Ng and K. Lee, “The Model Method: Singapore Children’s Tool for Representing and Solving Algebraic Word Problems,” 296.
• IBID, 296-297.
• L. Englard, “Raise the Bar on Problem Solving,” 157.
• S.F. Ng and K. Lee, “The Model Method: Singapore Children’s Tool for Representing and Solving Algebraic Word Problems,” 283.
• Y.K. Cheong, “The Model Method in Singapore,” 2002.
• S.F. Ng, K. Lee, S.Y. Ang, & F. Khng, “Model Method: obstacle or bridge to learning symbolic algebra,” 227-242.
• C.K. Looi and K.S. Lim, “From bar diagrams to letter-symbolic algebra: a technology-enabled bridging,” 358.
• IBID, p358.
• IBID, p 261
• http://www.corestandards.org/Math/Content/mathematics-glossary/Table-1/

Comments (1)

Send us your comment

A programme of:

• Observatory
• Innovative Solutions

Singapore Method: “Manipulating” Mathematics

The small asian archipelago of singapore has topped all international mathematics learning rankings for years: pisa, timss... nothing seems to beat singapore, a country that has led a great educational revolution and has developed, among other things, a mathematics teaching pedagogy that incorporates the best principles of learning into its daily lessons. this method has become very popular and is replicated all over the world. what’s special about it why does it succeed where traditional methods fail we’ll explain it to you in this post..

How are maths lessons developed in any primary school classroom in the world? The teacher poses a problem. The students look at the question and then work on solving it in their exercise books. They are alone facing the mathematical world. Armed with a pencil and a rubber, they pose and try to solve the calculations. Then someone comes to the board to solve it with the teacher. If the result and the calculations match those on the board, they have done it correctly. And then they start all over again. Memory, procedures that are not understood and lots and lots of calculations.

How does a maths class which uses the Singapore method work? The teacher poses a problem, and the students discuss how they will solve it together. Here we already have two of the main characteristics of this pedagogy: exploration and the construction of one’s own knowledge. Students contribute their ideas and solutions to the problem. The idea is to find the result using different paths to get there. Guided by the teacher, the students explore and discuss the problem together and, after analysing and solving it, they present their conclusions to others and reflect on them. All of this without having yet moved on to the individual calculations. First, understanding and reflecting on the learning process itself. Reasoning before calculating. Involving students in the whole process and teaching them to think for themselves. That is the approach.

Telling a story

Traditionally, discussion and storytelling have been far removed from maths classes, but with the Singapore method this is not the case. As we will see, based on the three phases of the method, the pupils tell a mathematical story, starting from a specific situation inspired by their everyday life.

The method proposes a sequential acquisition of mathematical knowledge, known as the C-P-A approach :

• Concrete phase: the problem is presented in a concrete way, giving priority to manipulation and exploration. The students discover mathematical notions through the manipulation of concrete, real objects that they have to hand.
• Pictorial or visual phase: students create a graphical representation of the relationships between the quantities or the underlying mathematical processes that solve the challenge or problem. The objects are replaced by images, using bar models.
• Abstract phase: this third stage links these processes with the algorithms and formulations of more abstract mathematics. We find the corresponding mathematical calculation.

The Singapore Method website lists the main pedagogical rules of the method. These are:

• Spiral progression curriculum: as opposed to the traditional linear progression curriculum, this curriculum design involves the reinforcement of prior knowledge with the teaching of new knowledge, which reinforces learning and contextualises it as a whole. Reviewing what has already been learnt and making sense of it in a new context generates meaningful and comprehensive learning, as opposed to merely operational learning with a linear curriculum design.
• The bar model : one of the most powerful and relevant of all modelling strategies (though not the only one), due to its versatility and application possibilities. The model helps students to have a greater understanding of concepts such as fractions, ratios or percentages; to establish a step-by-step plan for solving arithmetic problems; to make comparisons; and to engage in solving challenging problems. It also develops students’ lateral and creative thinking.
• Algebraic thinking: functional relationships, patterns and numerical relationships etc., always using the spiral curriculum and presenting each lesson on previously learnt concepts.
• The C-P-A approach: Concrete, Pictorial, Abstract. We have already discussed the three sequential phases of the method.
• Teaching model connected to learning objectives: teachers who use the Singapore method approach their teaching based on a variety of influences from psychologists, educators and mathematicians combining behavioural trends and cognitive psychology, among others.

Teachers using the Singapore method: drivers of change

What is the role of the teacher in this teaching method? What challenges do they face in applying this methodology, which is so different from more traditional ways of teaching?

As we have seen, in applying the Singapore method, the main role of the teacher is to encourage participation in discussion and collaboration among their students. They become a kind of facilitator who guides their students in the problem-solving process. We could also say that they become one of the learners themselves, by participating in the ideas and solutions proposed by their pupils. This can pose some challenges for teachers:

• High adaptability: in this regard, the teacher must make a 180-degree turn in their teaching methods. Class lectures in which the teacher does all the talking and the students just listen are no longer useful. The Singapore method works with students in a collaborative way.
• Understanding the students’ proposals: as a consequence of using this method, by letting the children think about the solution to the problem for themselves, the teacher who intends to apply this method must overcome the fear of not always understanding their students’ proposals and the way they think.
• The inertia of tradition: we teach as we were taught. That is a fact. A Singapore method teacher has to face the inertia of tradition, an endless loop of repetition of what they learnt from their teachers in the past.
• Deep conviction: in order to be able to apply this method, a deep understanding and conviction is required, the result of intense reflection on the very nature of teaching maths.

In short, this method teaches strategies that help students to visualise and conceptualise problems to gain greater control of “mental arithmetic”, as well as to strengthen their skills in problem-solving in a creative way, substantially improving their passion for mathematics, which is vital.

This method, part of a profound revolution in education and teaching, has led a small and poor country which had few prospects for the future only 50 years ago, to become one of the most prosperous states in the world. A small example of the transformative power of education.

If you would like to know more details about this method, visit the website in Spanish. You can also find out more about the method on the international website .

You may also be interested in…

Observatory Inspiring Experiences

Observatory Trends

Observatory 21st Century Skills

The Classical Classroom

A glimpse inside Hillsdale College's network of classical schools across the country.

How Bar Modeling Makes Word Problems Easy in Singapore Math

To help teachers and parents understand Singapore math, I’ve been writing about how although it can seem difficult at first, it’s actually a common-sense approach to mathematics that really gets results. Before you read this post, take a look at an introduction to Singapore math here.

One of the most recognizable parts of Singapore math is bar modeling, an approach to solving complex problems using pictures. Singapore math makes sense to students because it always begins with concrete objects, then moves to pictorial representations, and only then uses symbols.

We’ve all had the experience of looking at a complicated word problem and not being sure where to begin. In the early days of working in a classical school, I spoke to so many students who were overwhelmed by word problems because they had been trying to understand them all at once. With bar modeling, students learn how to break down word problems into their parts, and understand them visually. With bar modeling, complex things suddenly become simple and and math anxiety seems to vanish.

Let’s look at an example. First we’ll solve it using regular algebra, and then we’ll use bar modeling to see how much easier it can be.

Here’s a 5th grade math problem.

Unless you regularly come across ratio problems in your daily life, or have recently taken an algebra course recently, this problem is probably a little daunting. A high school algebra student might know what to do, but in Singapore math, a 5th grader can solve it with ease. Let’s do the high school algebra approach first, and then use bar modeling.

The Algebra Method

Here’s the problem again.

We’ll begin by defining the relationships between each of the pastries.

We want to have all of the variables in terms of d because we are looking for the number of donuts. 

Now, let’s solve it using algebra.

Since m=6s and m=2d , we can use the transitive property to see that 6s=2d . Therefore,

Now we simply have to substitute 2d for m and d/3 for s into the equation that included all of our variables (m+s+d=170) , and then solve for d .

Now we can simply divide, and solve. Here’s our answer:

Pretty complicated, right? Now let’s tackle this same problem using bar modeling, the same way a 5th grader would do it in Singapore math.

The Bar Modeling Method

First, we read through the entire problem to get an overall sense of what we are looking for. Then, we re-read the problem more slowly, stopping when we can represent a quantity or relationship between quantities with a picture. Read, then stop, then draw. Then keep reading.

Here’s our problem again.

We’ll read it piece by piece, drawing each essential piece of information.

“I have 6 times as many muffins as scones”

We’ll use bars to draw the relationship between muffins and scones.

“and twice as many muffins as donuts.”

We’ll add some bars of the right length to show the relationship of donuts to muffins.

“I have 170 pastries altogether.”

We’ll use a bracket to show the total number.

“How many donuts do I have?”

And we’ll add a question mark next to the information the problem is asking us to find.

At this point, we have created a picture that captures the information in the entire word problem. One of the beautiful things about bar modeling is that we can now just think in pictures, rather than words. It’s one step less abstract, which is always helpful in math.

Now we solve.

Let’s look at what we’ve got. We’ve drawn a total of 10 equally sized bars up there, and our bracket shows us that all of those together equal 170 pastries.

Therefore, 1 bar represents 17 pastries.

Let’s look at the blue bars, which symbolize the donuts, the number we’re looking for.

Since the number of donuts is represented by 3 bars, we know that there are 51 donuts, because 17 times 3 is 51.

There we go. 51 donuts.

As you can see from this example, the bar modeling makes this problem more approachable by breaking it into manageable parts and giving a place to start. Just as with this example, bar modeling can be used almost universally on problems beginning in 2 nd grade through algebra. While this is true, it is important to remember that the primary reason for bar modeling is to help transition to the abstract.

The process for working through this problem is nearly the same for both the bar model and the algebra, so by adding the pictorial element of the bar model, the move to the abstract nature of the algebra is much clearer and continuous.

Share this:

• Already have a WordPress.com account? Log in now.
• Subscribe Subscribed
• Copy shortlink
• Report this content
• View post in Reader
• Manage subscriptions
• Collapse this bar

• WordPress.org
• Documentation
• Learn WordPress

SingaporeMathSource

• Singapore Math Source Quick Start Guide
• Singapore Math Curriculum
• Scope and Sequences
• In the News
• Schools in the News
• Favorite Printable Resources
• Primary Mathematics vs. Math in Focus
• Best Books to Support Singapore Math in the Classroom
• Best Books for Grown-Ups Wanting to Learn Singapore Math
• Fun Math Practice Sites
• Math Wall ideas
• Assessments
• Handouts from Trainings
• Jumpstart Your Singapore Math 2024
• Jumpstart your Singapore Math Online
• Member Access – Jumpstart Your Singapore Math For Schools
• Math Champions Professional Development
• What attendees are saying!

Guest Post – Problem Solving: The Heart of Singapore Math

This article originally was featured in the fall 2018 issue of St. Anne’s-Belfield School’s  Perspectives  magazine and is republished with both the school and author’s permission.

The author, Sara Kronstain, has almost a decade of experience guiding elementary and middle school mathematicians to become critical thinkers and problem solvers.  She teaches fifth-grade math and is the Kindergarten-6th Grade Math Department Chair at St. Anne’s-Belfield School in Charlottesville, Virginia.

Problem-Solving: The Heart of Singapore Math

When I was in school, my math classes were typical of what one would expect a “traditional” math class to look like. I remember sitting in my elementary and middle school classes, watching as my teachers modeled problem after problem. The class would listen and then practice many of the same types of problems in our notebooks. While this type of teaching may achieve the immediate goal of learning a mathematical procedure, it does not guide students to reach an integral part of learning mathematics: problem-solving (Cai & Lester, 2010).

Singapore Math is comprised of a framework with problem-solving being the center of learning mathematics. This framework is built around five key components – metacognition, process, attitudes, skills, and concepts – all being of equal importance in developing mathematical problem solving in students. Whereas traditional math classes may place primary importance on developing skills and concepts in students, the additional three components of metacognition (self-regulation of learning), process (reasoning, making connections, and applying knowledge), and attitudes (perseverance, confidence, interest) are all key to developing critical thinking and problem solving skills in students (Ministry of Education Singapore, 2006).

A typical Singapore Math lesson is taught with a concrete-pictorial-abstract approach. Where many of my lessons as a math student began in the abstract stage (solving equations), the concrete and pictorial stages allow students to create and solidify their own understanding of a topic. The concrete stage refers to using hands-on materials to model a mathematical situation.  The pictorial stage consists of diagrams and other visuals, thus building students’ learning in a tangible way (Maths No Problem!, 2018). The concrete and pictorial stages allow students to understand why math works the way it does before learning the procedure of how to solve using an algorithm.

Most Singapore Math lessons begin with an anchor task, allowing students to explore these three stages. The anchor task is a question that allows students the chance to deeply explore a topic and develop multiple methods for solving a problem (Ban Har, 2013). Let us say, for example, a group of fifth graders were posed the problem, “The distance of a race is 3km. Lily ran two-fifths of the distance. How many kilometers did Lily run?”  Students would be given the opportunity to freely explore this question by using manipulatives such as fraction bars, fractions circles, or paper (for folding) along with writing materials. Here are a few examples of possible student responses to this question:

Method: Repeated Addition

Add ⅖ + ⅖ + ⅖ .  Students may use fraction bars, fraction circles, or pictures.  Students become familiar with the phrase “3 groups of ⅖”.

Method: Bars

Three boxes are each split into fifths. Two of each of the fifths in all three boxes are shaded in.  The shaded parts are added together.

Method: Bar Model

A bar with the length of 3 wholes can be split into five parts.  Each part has a value of ⅗. Then add ⅗ + ⅗ .

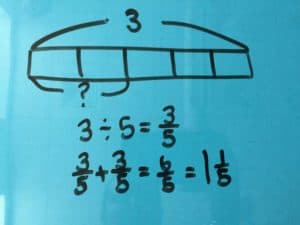
Method: Addition with Fractions

Three boxes are split into 5 equal groups, first by placing one half in each group. Then, split the leftover half into five parts (tenths). Each group will have one half of a whole and one tenth of a whole. Combine two groups by adding two halves to two tenths.

In this example, the repeated addition method reinforces addition with fractions, while the last method has students thinking about and manipulating fractions in a much more complex way.  Thinking back to the five key components of Singapore Math, students in this example are refining their process of learning operations with fractions by making connects across operations.  It is powerful that these responses are coming from students, as they are building their understanding of math through collaboration with their peers. In sharing methods, listening to other’s methods, and processing others methods, students are also developing their metacognition. This question could also be modified and challenge students to problem solve in an even deeper way. “What if the total distance was ½ km?  What if the total distance was 3 ½ km?”  Students can then go back to the concrete, pictorial, and abstract stages and continue to build on their problem-solving abilities.

At the end of the day the primary purpose of this math lesson, or any math lesson for that matter, is not simply to learn how to multiply fractions by a whole number. The most important takeaways are the critical thinking, questioning, collaboration, and problem-solving that happens among students. Teachers are not preparing students to go out into a world where they will simply be asked to recite an algorithm. While a goal is for each child to develop a deep love of math, the biggest hope is that students learn to ask questions, logically think through problems, and make sense of the world around them.

Ban Har, Yeap.  (2013, June 13).  Singapore Math at the Blake School, Hopkins, MN.  Retrieved from http://banhar.blogspot.com/search?q=anchor+task

Cai, Jinfa, & Lester, Frank. (2010, April 8).  Problem Solving. National Council of Teachers of Mathematics.   Retrieved from https://www.nctm.org/Research-and-Advocacy/Research-Brief-and-Clips/Problem-Solving/#brief

Kaur, Berinderjeet.  (2018, March 29).  Building the Maths house: Singapore’s curriculum framework.  Oxford Education Blog .  Retrieved from https://educationblog.oup.com/secondary/maths/building-the-maths-house-singapores-curriculum-framework

Ministry of Education Singapore.  (2006).  Mathematics Syllabus Primary .  Retrieved from https://www.moe.gov.sg/docs/default-source/document/education/syllabuses/sciences/files/2007-mathematics-%28primary%29-syllabus.pdf

Maths No Problem! (2018). Concrete Pictorial Abstract.   Retrieved from https://mathsnoproblem.com/en/the-maths/teaching-methods/concrete-pictorial-abstract/

Speak Your Mind Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed .

Your Host, Cassandra Turner

Find Us Near You

Find us on the web.

We’ve trained teachers in 47 States!

What Teachers are Saying

We’re on instagram.

mathchampions

We create customized math training/coaching PD for your school. How can we help you improve your math instruction?

Blog Categories

• Implementing Singapore Math (29)
• Masters (1)
• Math Events (64)
• Math Resources (158)
• Schools (15)
• Singapore Math Problems (41)
• Tales from the classroom (41)
• Training (47)
• Uncategorized (3)
• Word Problem Wednesday (31)

Pinterest Faves

Copyright © 2008 - 2024 · Cassandra Turner · Site Design by Heather Mackan Creative · Built on Genesis

Return to top of page

Theoretical Framework of the Singapore Method

In this post, we are going to talk about the Theoretical Framework of the Singapore Method, which revolves around mathematical problem-solving.

The Singapore Method groups mathematical concepts into 6 sections:

• Probability

These content categories are closely related and are interdependent. In the different stages of learning, like in different programs, the extent and depth of the content varies.

The Singapore Method works on skills like:

• Numerical calculation
• Algebraic manipulation
• Spatial visualization
• Data analysis
• Measurements
• Use of mathematical tools
• In addition, it also develops the ability to use spreadsheets and software to facilitate mathematics learning.

All of these skills are taught in a way that it instrumental, comprehensive, and justified.

Metacognition

Metacognition, or thinking about thinking, refers to the consciousness and the ability to control, regulate, and evaluate the processes of thought. In particular, it alludes to the selection and use of strategies to solve problems.

To develop consciousness and metacognitive strategies, students that follow the Singapore method should confront the resolution to problems as being open and non-routine . At the same time, they have to discuss their solutions, think aloud, and reflect on what they are doing – all the while maintaining an updated record on how things are progressing.

The attitudes consist of the affective aspects of learning mathematics, such as:

• Beliefs about mathematics and it’s usefulness
• Interest and enjoyment of learning mathematics
• Appreciation of the beauty of mathematics
• Confidence in the use of mathematics
• Perseverance in problem-solving

They are very consistent with the fact that student’s attitudes toward mathematics are shaped by their learning experiences. By making learning fun, meaningful, and relevant it helps to instill positive attitudes towards subjects.

The Singapore Method includes the following mathematical processes:

• Mathematical reasoning is the ability to analyze mathematical situations and construct logical arguments. It is a mental habit that can be developed through the application of mathematics in different contexts.
• Communication is the ability to use mathematical language to express ideas in a precise, concise, and logical way.
• Connections are the ability to see and establish links between mathematical ideas, between mathematics and other subjects, and between mathematics and the real world. All of these help students to really understand what they learn in mathematics.
• Mathematical modeling is the process of formulating a mathematical model to represent and solve real-world problems. Through mathematical models, students learn to cope with ambiguity, make connections, and select and apply appropriate mathematical concepts and skills. They also learn to identify assumptions and reflect on solutions to problems, as well as make informed decisions based on data given or compiled.
• Thinking skills, that is, the ability to classify, compare, and analyze problems in a global way.
• Heuristic thinking, is to say, the set of procedures that students use to address a problem whose solution is not an obvious one. This includes the use of representation (drawing a diagram), of conjecture (trial and error; make assumptions), to traverse the process (doing it backwards) and introducing changes to the problem (simplifying a problem; considering special cases).

References:

• Mathematics Syllabus. Primary. Ministry of Education Singapore.
• Smartick Lands in Singapore, a Country with One of the Most Challenging Education Systems in the World
• Singapore: Goals, Objectives, and Design of Its Curriculum

Learn More:

• Worked Examples and Metacognition
• Singapore: Experiences in Learning
• Teaching Principles and Learning Phases of Singapore Math
• Foundations of the Singapore Method in Math Instruction
• 15 fun minutes a day
• Adapts to your child’s level
• Millions of students since 2009

• Recent Posts

• The Language of Functions and Graphs - 07/01/2024
• Educational Technology: The Christodoulou Test - 05/06/2024
• Multiplication Activities in Smartick - 04/09/2024

Add a new public comment to the blog: Cancel reply

The comments that you write here are moderated and can be seen by other users. For private inquiries please write to [email protected]

Your personal details will not be shown publicly.

I have read and accepted the Privacy and Cookies Policy

The skills children pick up in math are indispensable; they can be applied to other academic subjects and to solve real-world problems in their daily lives and future work.

The Singapore Math curriculum focuses on problem solving. Through problem solving, children develop thinking skills such as creative thinking and critical thinking.

When children analyse math problems, they notice patterns, learn to generalise, form new ideas and activate their creative thinking. Children become critical thinkers when they are able to select the best strategy out of multiple methods to solve word problems.

Singapore Math Heuristics

In  part one of our Math Heuristics series , we gave an overview of the 12 problem-solving methods or heuristics taught in the Singapore primary math education syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to use them to solve various math word problems.

In  part two of the Math Heuristic series , we zoomed in on the heursitics – Act It Out, Draw A Diagram and Look For Patterns, and also showed how to apply the Polya’s 4-step problem-solving process in sample word problems.

In the third part of this series, we will focus on the next 3 heuristics –  Make a systematic list ,  guess and check , and  restate the problem in another way .

Sample word problems are solved using these 3 heuristics and Poly’s 4-step process in the step-by-step worked solutions provided by the curriculum team at S.A.M.

_______________________________________________________________________________________________________

Heuristic: Make a systematic list

Word Problem (Grade 2) :

Jimmy uses the number cards given below to form as many 3-digit odd numbers as he can. List all the numbers that Jimmy can form.

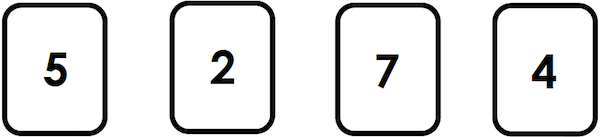
1. Understand: What to find: All the 3-digit odd numbers that Jimmy can form from the 4 number cards. What is known: Odd numbers end with 5 or 7.

2. Choose: Make a systematic list

Odd numbers that end with 5: 245 275 425 475 725 745

Odd numbers that end with 7: 247 257 427 457 527 547

Jimmy can form 12 3-digit odd numbers.

Did I form 3-digit numbers? Yes Did I form odd numbers? Yes Did I form all possible numbers? Yes

Try solving the following word problem using Polya’s 4-step process.

A shop sells apples in bags of 3. It sells lemons in bags of 4. Paul buys some bags of apples and lemons. He buys the same number of each fruit. He buys more than 20 and fewer than 30 pieces of each fruit. How many apples does Paul buy?

Heuristic: Guess and check

Word Problem (Grade 3) :

David sold a total of 15 $4 coupons and $5 coupons for a funfair. He received $65 for the sale of the coupons. How many $4 coupons and how many $5 coupons did he sell?

1. Understand: What to find: The number of $4 coupons and the number of $5 coupons David sold? What is known: He sold 15 coupons. He received $65.

2. Choose: Guess and check

$4 + $5 = $9. (7 × 9) = 63 is close to 65. I can start the first guess with 7 $4 coupons.

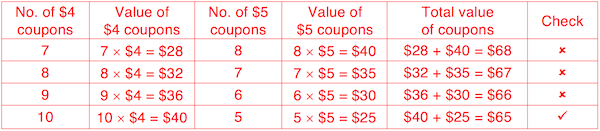
David sold 10 $4 coupons and 5 $5 coupons.

4. Check: What is the total number of coupons? 10 + 5 = 15 What is the total value of coupons? $40 + $25 = $65

Word Problem (Grade 5) :

In a quiz, 5 marks were awarded for each correct answer and 3 marks were deducted for each wrong answer. Darren answered 14 questions and scored 30 marks. How many questions did he answer correctly?

1. Understand: What to find: The number of questions Darren answered correctly. What is known: Add 5 marks for each correct answer. Minus 3 marks for each wrong answer. He answered 14 questions. He scored 30 marks.

I can start the first guess with the same number of correct answers and wrong answers.

Word Problem (Grade 5):

Vijay is presented with the equations below. Insert one pair of brackets in each equation to make it true. 4 × 11 + 18 ÷ 3 + 6 = 46

Heuristic: Restate the problem in another way

Sally has some beds and sofas. All of them are equal in length. The total length is 14 metres. Each bed is 2 metres long. Sally has 1 fewer bed than sofas. What is the total length of the sofas?

1. Understand: What to find: Total length of the sofas. What is known: Each bed is 2 metres long. Each sofa is 2 metres long. Total length of beds and sofas is 14 metres. Sally has 1 more sofa than bed.

2. Choose: Restate the problem in another way

If we add 1 more bed, Sally will have the same number of beds and sofas. New total length = 14 m + 2 m = 16 m Sally has the same number of beds and sofas Total length of sofas = 16 m ÷ 2 = 8 m

The total length of the sofas is 8 metres.

4. Check: How many sofas are there? 8 m ÷ 2 m = 4 How many beds are there? 4 – 1 = 3 How many beds and sofas altogether? 4 + 3 = 7 What is the total length of beds and sofas? 7 × 2 m = 14m

There are some identical pens and erasers. 2 pens and 3 erasers are 45 centimetres long altogether. 6 erasers and 2 pens are 60 centimetres long altogether. What is the length of 3 erasers?

These are just a few examples to show you how Singapore Math heuristics are used to solve basic and intermediate word problems in lower grade levels and complex word problems in upper grade levels.

Look out for parts four and five of this series for the other 6 remaining Singapore Math heuristics and word problems with step-by-step worked solutions.

This is the third part to S.A.M Math Heuristics series. Read  part one  and  part two  here.

Established in 2010, Seriously Addictive Mathematics (S.A.M) is the world’s largest Singapore Math enrichment program for children aged four to 12. The award-winning S.A.M program is based on the global top-ranking Singapore Math curriculum with a focus on developing problem solving and thinking skills.

The curriculum is complemented with S.A.M’s two-pillared approach of Classroom Engagement and Worksheet Reinforcement, with an individual learning plan tailored to each child at their own skill level and pace, because no two children learn alike.

Singapore Math Heuristics: Draw a Table, Make Suppositions and Use Before-After Concept

Heuristics, in the context of problem-solving, are a set of strategies to help students solve mathematical problems. Although problem-solving is by and large the process of working towards a goal to which a solution may not be immediately present, it is important that problem solvers (or students) are not only aware of what they are […]

Singapore Math Heuristics: Solve Part of the Problem, Simplify the Problem and Work Backwards

Problem-solving in mathematics helps children develop reasoning and communication skills that are transferrable and important life skills. Reasoning is required on three levels when children solve word problems. First, they use reasoning to recognise what information is provided or missing. Then, they use reasoning to figure out what information they need to find. Finally, they […]

Singapore Math Heuristics: Act It Out, Draw A Diagram, Look For Patterns

In part one of our Singapore Math Heuristics series, we gave an overview of the 12 heuristics in Singapore Primary Math syllabus, with tips from the curriculum team at Seriously Addictive Mathematics (S.A.M) on how to solve various math word problems using them. To recap, heuristics are methods or strategies students can use to solve complex […]

What are Singapore Math Heuristics?

Ever tried to help your child with primary math homework and got stumped? Today’s math questions can be challenging – even for adults. Math education is changing. While many parents spent time memorising procedures and formulas, today’s students are expected to not only understand and master the concepts, but also to have strong thinking skills […]

• Computer Vision
• Federated Learning
• Reinforcement Learning
• Natural Language Processing
• New Releases
• Advisory Board Members
• 🐝 Partnership and Promotion

Offline curation methods initially focused on the quality of textual captions and alignment with high-quality datasets, using pretrained models like CLIP and BLIP for filtering. These methods, however, fail to consider dependencies within batches. Cluster-level data pruning methods address this by reducing semantic redundancy and using core-set selection, but these are heuristic-based and decoupled from training objectives. Online data curation adapts during learning, addressing the limitations of fixed strategies. Hard negative mining optimizes the selection of challenging examples, while model approximation techniques allow smaller models to act as proxies for larger ones, enhancing data selection efficiency during training.

The method selects the most relevant data sub-batches from a larger super-batch using model-based scoring functions, considering losses from both the learner and pretrained reference models. Prioritizing high-loss batches for the learner can discard trivial data but may also up-sample noise. Alternatively, selecting low-loss data for the reference model can identify high-quality examples but may be overly dependent on the reference model. Combining these approaches, learnability scoring prioritizes unlearned and learnable data, accelerating large-scale learning. Efficient scoring with online model approximation and multi-resolution training further optimizes the process.

The efficacy of JEST for forming learnable batches was evaluated, revealing that JEST rapidly increases batch learnability with few iterations. It outperforms independent selection, achieving performance comparable to brute-force methods. In multimodal learning, JEST significantly accelerates training and improves final performance, with benefits scaling with filtering ratios. Flexi-JEST, a compute-efficient variant using multi-resolution training, also reduces computational overhead while maintaining speedups. JEST’s performance improves with stronger data curation, and it surpasses prior models on multiple benchmarks, demonstrating effectiveness in both training and compute efficiency.

In conclusion, The JEST method, designed for jointly selecting the most learnable data batches, significantly accelerates large-scale multimodal learning, achieving superior performance with up to 10× fewer FLOPs and 13× fewer examples. It highlights the potential for “data quality bootstrapping,” where small curated datasets guide learning on larger, uncurated ones. Unlike static dataset filtering, which can limit performance, online construction of useful batches enhances pretraining efficiency. This suggests that foundation distributions can effectively replace generic foundation datasets, whether through pre-scored datasets or dynamically adjusted with learnability JEST. However, the method relies on small, curated reference datasets, indicating a need for future research to infer reference datasets from downstream tasks.

Check out the Paper . All credit for this research goes to the researchers of this project. Also, don’t forget to follow us on  Twitter . 

Join our  Telegram Channel and  LinkedIn Gr oup .

If you like our work, you will love our  newsletter..

Don’t Forget to join our  46k+ ML SubReddit

Sana Hassan

Sana Hassan, a consulting intern at Marktechpost and dual-degree student at IIT Madras, is passionate about applying technology and AI to address real-world challenges. With a keen interest in solving practical problems, he brings a fresh perspective to the intersection of AI and real-life solutions.

• Deep Learning in Protein Engineering: Designing Functional Soluble Proteins
• Microsoft's Comprehensive Four-Stage AI Learning Journey: Empowering Businesses with Skills for Effective AI Integration and Innovation
• Enhancing Vision-Language Models: Addressing Multi-Object Hallucination and Cultural Inclusivity for Improved Visual Assistance in Diverse Contexts
• D-Rax: Enhancing Radiologic Precision through Expert-Integrated Vision-Language Models

RELATED ARTICLES MORE FROM AUTHOR

Numinamath 7b tir released: transforming mathematical problem-solving with advanced tool-integrated reasoning and python repl for competition-level accuracy, this ai paper from the national university of singapore introduces a defense against adversarial attacks on llms utilizing self-evaluation, sensetime unveiled sensenova 5.5: setting a new benchmark to rival gpt-4o in 5 out of 8 key metrics, theoremllama: an end-to-end framework to train a general-purpose large language model to become a lean4 expert, future-proofing the past: ai’s role in protecting cultural legacies, open contracts: the free and open source document analytics platform, numinamath 7b tir released: transforming mathematical problem-solving with advanced tool-integrated reasoning and python repl..., this ai paper from the national university of singapore introduces a defense against adversarial..., sensetime unveiled sensenova 5.5: setting a new benchmark to rival gpt-4o in 5 out..., theoremllama: an end-to-end framework to train a general-purpose large language model to become a....

• AI Magazine
• Privacy & TC
• Cookie Policy

🐝 FREE AI Courses on RAG + Deployment of an Healthcare AI App + LangChain Colab Notebook all included

Thank You 🙌

Privacy Overview