- PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
- EDIT Edit this Article
- EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
- Browse Articles
- Learn Something New
- Quizzes Hot
- This Or That Game
- Train Your Brain
- Explore More
- Support wikiHow
- About wikiHow
- Log in / Sign up
- Education and Communications
- Mathematics

How to Solve a Quadratic Equation: A Step-by-Step Guide
Last Updated: May 27, 2024 Fact Checked
Factoring the Equation
Using the quadratic formula, completing the square, practice problems and answers, expert q&a.
This article was co-authored by David Jia . David Jia is an Academic Tutor and the Founder of LA Math Tutoring, a private tutoring company based in Los Angeles, California. With over 10 years of teaching experience, David works with students of all ages and grades in various subjects, as well as college admissions counseling and test preparation for the SAT, ACT, ISEE, and more. After attaining a perfect 800 math score and a 690 English score on the SAT, David was awarded the Dickinson Scholarship from the University of Miami, where he graduated with a Bachelor’s degree in Business Administration. Additionally, David has worked as an instructor for online videos for textbook companies such as Larson Texts, Big Ideas Learning, and Big Ideas Math. There are 9 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 1,421,140 times.
A quadratic equation is a polynomial equation in a single variable where the highest exponent of the variable is 2. [1] X Research source There are three main ways to solve quadratic equations: 1) to factor the quadratic equation if you can do so, 2) to use the quadratic formula, or 3) to complete the square. If you want to know how to master these three methods, just follow these steps.
Quadradic Formula for Solving Equations

- Then, use the process of elimination to plug in the factors of 4 to find a combination that produces -11x when multiplied. You can either use a combination of 4 and 1, or 2 and 2, since both of those numbers multiply to get 4. Just remember that one of the terms should be negative, since the term is -4. [3] X Research source

- 3x = -1 ..... by subtracting
- 3x/3 = -1/3 ..... by dividing
- x = -1/3 ..... simplified
- x = 4 ..... by subtracting
- x = (-1/3, 4) ..... by making a set of possible, separate solutions, meaning x = -1/3, or x = 4 seem good.

- So, both solutions do "check" separately, and both are verified as working and correct for two different solutions.

- 4x 2 - 5x - 13 = x 2 -5
- 4x 2 - x 2 - 5x - 13 +5 = 0
- 3x 2 - 5x - 8 = 0

- {-b +/-√ (b 2 - 4ac)}/2
- {-(-5) +/-√ ((-5) 2 - 4(3)(-8))}/2(3) =
- {-(-5) +/-√ ((-5) 2 - (-96))}/2(3)

- {-(-5) +/-√ ((-5) 2 - (-96))}/2(3) =
- {5 +/-√(25 + 96)}/6
- {5 +/-√(121)}/6

- (5 + 11)/6 = 16/6
- (5-11)/6 = -6/6

- x = (-1, 8/3)

- 2x 2 - 9 = 12x =
- In this equation, the a term is 2, the b term is -12, and the c term is -9.

- 2x 2 - 12x - 9 = 0
- 2x 2 - 12x = 9

- 2x 2 /2 - 12x/2 = 9/2 =
- x 2 - 6x = 9/2

- -6/2 = -3 =
- (-3) 2 = 9 =
- x 2 - 6x + 9 = 9/2 + 9

- x = 3 + 3(√6)/2
- x = 3 - 3(√6)/2)

- If the number under the square root is not a perfect square, then the last few steps run a little differently. Here is an example: [14] X Research source Thanks Helpful 0 Not Helpful 0
- If the "b" is an even number, the formula is : {-(b/2) +/- √(b/2)-ac}/a. Thanks Helpful 3 Not Helpful 0
- As you can see, the radical sign did not disappear completely. Therefore, the terms in the numerator cannot be combined (because they are not like terms). There is no purpose, then, to splitting up the plus-or-minus. Instead, we divide out any common factors --- but ONLY if the factor is common to both of the constants AND the radical's coefficient. Thanks Helpful 1 Not Helpful 0

You Might Also Like

- ↑ https://www.mathsisfun.com/definitions/quadratic-equation.html
- ↑ https://www.mathsisfun.com/algebra/factoring-quadratics.html
- ↑ https://www.mathportal.org/algebra/solving-system-of-linear-equations/elimination-method.php
- ↑ https://www.cuemath.com/algebra/quadratic-equations/
- ↑ https://www.purplemath.com/modules/solvquad4.htm
- ↑ http://www.purplemath.com/modules/quadform.htm
- ↑ https://uniskills.library.curtin.edu.au/numeracy/algebra/quadratic-equations/
- ↑ http://www.mathsisfun.com/algebra/completing-square.html
- ↑ https://www.umsl.edu/~defreeseca/intalg/ch7extra/quadmeth.htm
About This Article

To solve quadratic equations, start by combining all of the like terms and moving them to one side of the equation. Then, factor the expression, and set each set of parentheses equal to 0 as separate equations. Finally, solve each equation separately to find the 2 possible values for x. To learn how to solve quadratic equations using the quadratic formula, scroll down! Did this summary help you? Yes No
- Send fan mail to authors
Reader Success Stories
Sep 24, 2022
Did this article help you?
Kalo Morris
Mar 12, 2017
Matthew Mathers
Mar 25, 2017
Kapela Davis
Oct 10, 2017
Jan 29, 2018

Featured Articles

Trending Articles

Watch Articles

- Terms of Use
- Privacy Policy
- Do Not Sell or Share My Info
- Not Selling Info
Don’t miss out! Sign up for
wikiHow’s newsletter
Quadratic Equation
Quadratic equations are second-degree algebraic expressions and are of the form ax 2 + bx + c = 0. The term "quadratic" comes from the Latin word "quadratus" meaning square, which refers to the fact that the variable x is squared in the equation. In other words, a quadratic equation is an “equation of degree 2.” There are many scenarios where a quadratic equation is used. Did you know that when a rocket is launched, its path is described by a quadratic equation? Further, a quadratic equation has numerous applications in physics, engineering, astronomy, etc.
Quadratic equations have maximum of two solutions, which can be real or complex numbers. These two solutions (values of x) are also called the roots of the quadratic equations and are designated as (α, β). We shall learn more about the roots of a quadratic equation in the below content.
| 1. | |
| 2. | |
| 3. | |
| 4. | |
| 5. | |
| 6. | |
| 7. | |
| 8. | |
| 9. | |
| 10. | |
| 11. | |
| 12. |
What is Quadratic Equation?
A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form, the x 2 term is written first, followed by the x term, and finally, the constant term is written.
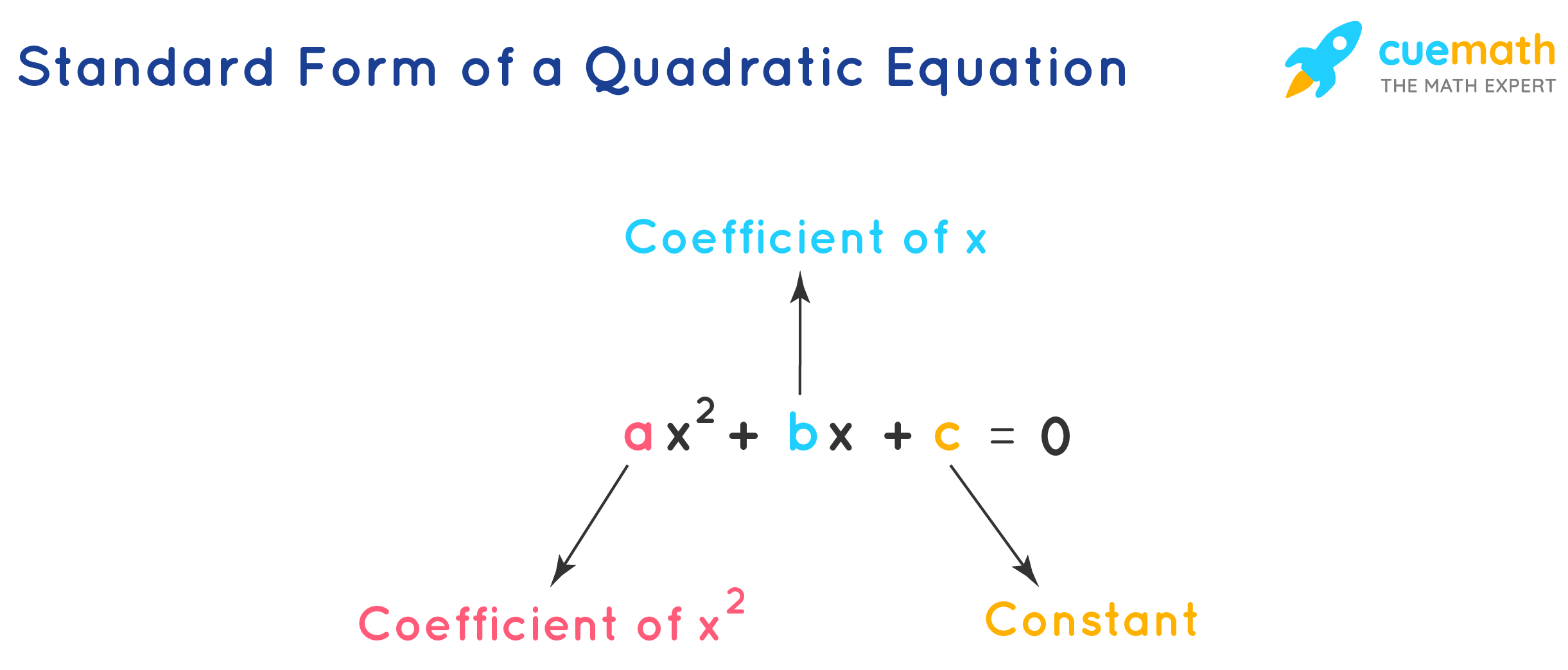
Further, in real math problems the quadratic equations are presented in different forms: (x - 1)(x + 2) = 0, -x 2 = -3x + 1, 5x(x + 3) = 12x, x 3 = x(x 2 + x - 3). All of these equations need to be transformed into standard form of the quadratic equation before performing further operations.
Roots of a Quadratic Equation
The roots of a quadratic equation are the two values of x, which are obtained by solving the quadratic equation. These roots of the quadratic equation are also called the zeros of the equation. For example, the roots of the equation x 2 - 3x - 4 = 0 are x = -1 and x = 4 because each of them satisfies the equation. i.e.,
- At x = -1, (-1) 2 - 3(-1) - 4 = 1 + 3 - 4 = 0
- At x = 4, (4) 2 - 3(4) - 4 = 16 - 12 - 4 = 0
There are various methods to find the roots of a quadratic equation. The usage of the quadratic formula is one of them.
Quadratic Formula
Quadratic formula is the simplest way to find the roots of a quadratic equation . There are certain quadratic equations that cannot be easily factorized, and here we can conveniently use this quadratic formula to find the roots in the quickest possible way. The two roots in the quadratic formula are presented as a single expression. The positive sign and the negative sign can be alternatively used to obtain the two distinct roots of the equation.
Quadratic Formula: The roots of a quadratic equation ax 2 + bx + c = 0 are given by x = [-b ± √(b 2 - 4ac)]/2a.
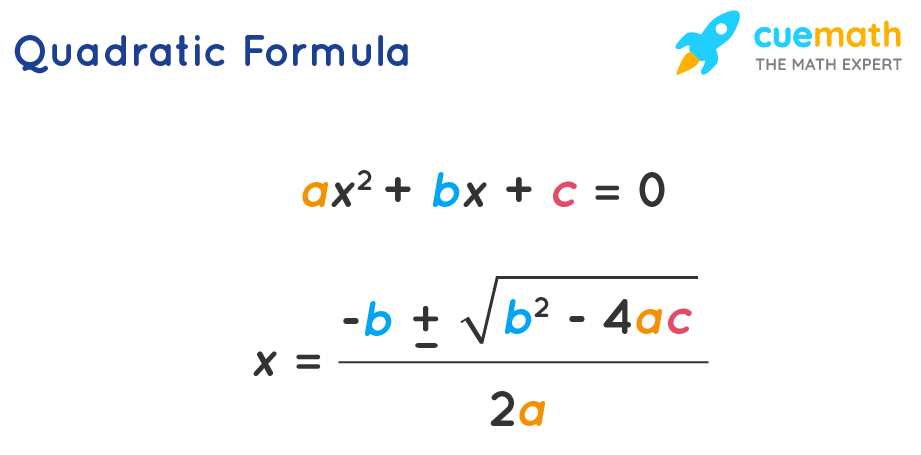
This formula is also known as the Sridharacharya formula .
Example: Let us find the roots of the same equation that was mentioned in the earlier section x 2 - 3x - 4 = 0 using the quadratic formula.
a = 1, b = -3, and c = -4.
x = [-b ± √(b 2 - 4ac)]/2a = [-(-3) ± √((-3) 2 - 4(1)(-4))]/2(1) = [3 ± √25] / 2 = [3 ± 5] / 2 = (3 + 5)/2 or (3 - 5)/2 = 8/2 or -2/2 = 4 or -1 are the roots.
Proof of Quadratic Formula
Consider an arbitrary quadratic equation: ax 2 + bx + c = 0, a ≠ 0
To determine the roots of this equation, we proceed as follows:
ax 2 + bx = -c ⇒ x 2 + bx/a = -c/a
Now, we express the left-hand side as a perfect square , by introducing a new term (b/2a) 2 on both sides:
- x 2 + bx/a + (b/2a) 2 = -c/a + (b/2a) 2
The left-hand side is now a perfect square:
(x + b/2a) 2 = -c/a + b 2 /4a 2 ⇒ (x + b/2a) 2 = (b 2 - 4ac)/4a 2
This is good for us, because now we can take square roots to obtain:
x + b/2a = ±√(b 2 - 4ac)/2a
x = (-b ± √(b 2 - 4ac))/2a
Thus, by completing the squares, we were able to isolate x and obtain the two roots of the equation.
Nature of Roots of the Quadratic Equation
The roots of a quadratic equation are usually represented to by the symbols alpha (α), and beta (β). Here we shall learn more about how to find the nature of roots of a quadratic equation without actually finding the roots of the equation.
The nature of roots of a quadratic equation can be found without actually finding the roots (α, β) of the equation. This is possible by taking the discriminant value, which is part of the formula to solve the quadratic equation. The value b 2 - 4ac is called the discriminant of a quadratic equation and is designated as 'D'. Based on the discriminant value the nature of the roots of the quadratic equation can be predicted.
Discriminant: D = b 2 - 4ac
- D > 0, the roots are real and distinct
- D = 0, the roots are real and equal.
- D < 0, the roots do not exist or the roots are imaginary .

Now, check out the formulas to find the sum and the product of the roots of the equation.
Sum and Product of Roots of Quadratic Equation
The coefficient of x 2 , x term, and the constant term of the quadratic equation ax 2 + bx + c = 0 are useful in determining the sum and product of the roots of the quadratic equation. The sum and product of the roots of a quadratic equation can be directly calculated from the equation, without actually finding the roots of the quadratic equation. For a quadratic equation ax 2 + bx + c = 0, the sum and product of the roots are as follows.
- Sum of the Roots: α + β = -b/a = - Coefficient of x/ Coefficient of x 2
- Product of the Roots: αβ = c/a = Constant term/ Coefficient of x 2
Writing Quadratic Equations Using Roots
The quadratic equation can also be formed for the given roots of the equation. If α, β, are the roots of the quadratic equation, then the quadratic equation is as follows.
x 2 - (α + β)x + αβ = 0
Example: What is the quadratic equation whose roots are 4 and -1?
Solution: It is given that α = 4 and β = -1. The corresponding quadratic equation is found by:
x 2 - (α + β)x + αβ = 0 x 2 - (α + β)x + αβ = 0 x 2 - (4 - 1)x + (4)(-1) = 0 x 2 - 3x - 4 = 0
Formulas Related to Quadratic Equations
The following list of important formulas is helpful to solve quadratic equations.
- The quadratic equation in its standard form is ax 2 + bx + c = 0
- For D > 0 the roots are real and distinct.
- For D = 0 the roots are real and equal.
- For D < 0 the real roots do not exist, or the roots are imaginary.
- The formula to find the roots of the quadratic equation is x = [-b ± √(b 2 - 4ac)]/2a.
- The sum of the roots of a quadratic equation is α + β = -b/a.
- The product of the Root of the quadratic equation is αβ = c/a.
- The quadratic equation whose roots are α, β, is x 2 - (α + β)x + αβ = 0.
- The condition for the quadratic equations a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0 having the same roots is (a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2 .
- When a > 0, the quadratic expression f(x) = ax 2 + bx + c has a minimum value at x = -b/2a.
- When a < 0, the quadratic expression f(x) = ax 2 + bx + c has a maximum value at x = -b/2a.
- The domain of any quadratic function is the set of all real numbers.
Methods to Solve Quadratic Equations
A quadratic equation can be solved to obtain two values of x or the two roots of the equation. There are four different methods to find the roots of the quadratic equation. The four methods of solving the quadratic equations are as follows.
- Factorizing of Quadratic Equation
- Using quadratic formula (which we have seen already)
Method of Completing the Square
- Graphing Method to Find the Roots
Let us look in detail at each of the above methods to understand how to use these methods, their applications, and their uses.
Solving Quadratic Equations by Factorization
Factorization of quadratic equation follows a sequence of steps. For a general form of the quadratic equation ax 2 + bx + c = 0, we need to first split the middle term into two terms, such that the product of the terms is equal to the constant term. Further, we can take the common terms from the available term, to finally obtain the required factors as follows:
- x 2 + (a + b)x + ab = 0
- x 2 + ax + bx + ab = 0
- x(x + a) + b(x + a)
- (x + a)(x + b) = 0
Here is an example to understand the factorization process.
- x 2 + 5x + 6 = 0
- x 2 + 2x + 3x + 6 = 0
- x(x + 2) + 3(x + 2) = 0
- (x + 2)(x + 3) = 0
Thus the two obtained factors of the quadratic equation are (x + 2) and (x + 3). To find its roots, just set each factor to zero and solve for x. i.e., x + 2 = 0 and x + 3 = 0 which gives x = -2 and x = -3. Thus, x = -2 and x = -3 are the roots of x 2 + 5x + 6 = 0.
Further, there is another important method of solving a quadratic equation. The method of completing the square for a quadratic equation is also useful to find the roots of the equation.
The method of completing the square in a quadratic equation is to algebraically square and simplify, to obtain the required roots of the equation. Consider a quadratic equation ax 2 + bx + c = 0, a ≠ 0. To determine the roots of this equation, we simplify it as follows:
- ax 2 + bx + c = 0
- ax 2 + bx = -c
- x 2 + bx/a = -c/a
Now, we express the left-hand side as a perfect square, by introducing a new term (b/2a) 2 on both sides:
- (x + b/2a) 2 = -c/a + b 2 /4a 2
- (x + b/2a) 2 = (b 2 - 4ac)/4a 2
- x + b/2a = + √(b 2 - 4ac)/2a
- x = - b/2a + √(b 2 - 4ac)/2a
- x = [-b ± √(b 2 - 4ac)]/2a
Here the '+' sign gives one root and the '-' sign gives another root of the quadratic equation. Generally, this detailed method is avoided, and only the quadratic formula is used to obtain the required roots.
Graphing a Quadratic Equation
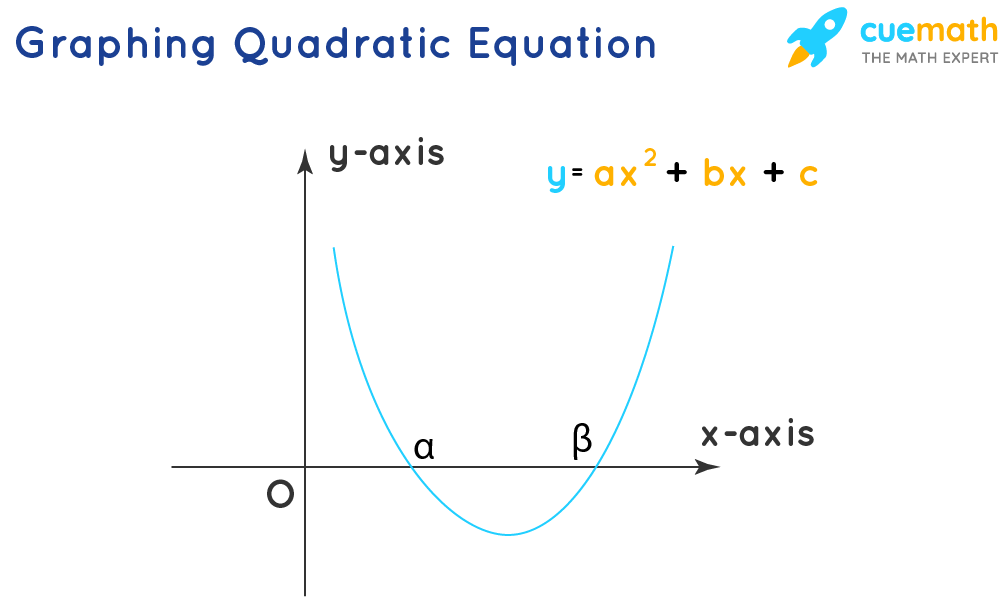
The point(s) where the graph cuts the horizontal x-axis (typically the x-intercepts ) is the solution of the quadratic equation. These points can also be algebraically obtained by equalizing the y value to 0 in the function y = ax 2 + bx + c and solving for x.
Quadratic Equations Having Common Roots
Consider two quadratic equations having common roots a 1 x 2 + b 1 x + c 1 = 0, and a 2 x 2 + b 2 x + c 2 = 0. Let us solve these two equations to find the conditions for which these equations have a common root. The two equations are solved for x 2 and x respectively.
(x 2 )(b 1 c 2 - b 2 c 1 ) = (-x)/(a 1 c 2 - a 2 c 1 ) = 1/(a 1 b 2 - a 2 b 1 )
x 2 = (b 1 c 2 - b 2 c 1 ) / (a 1 b 2 - a 2 b 1 )
x = (a 2 c 1 - a 1 c 2 ) / (a 1 b 2 - a 2 b 1 )
Hence, by simplifying the above two expressions we have the following condition for the two equations having the common root.
(a 1 b 2 - a 2 b 1 ) (b 1 c 2 - b 2 c 1 ) = (a 2 c 1 - a 1 c 2 ) 2
Maximum and Minimum Value of Quadratic Expression
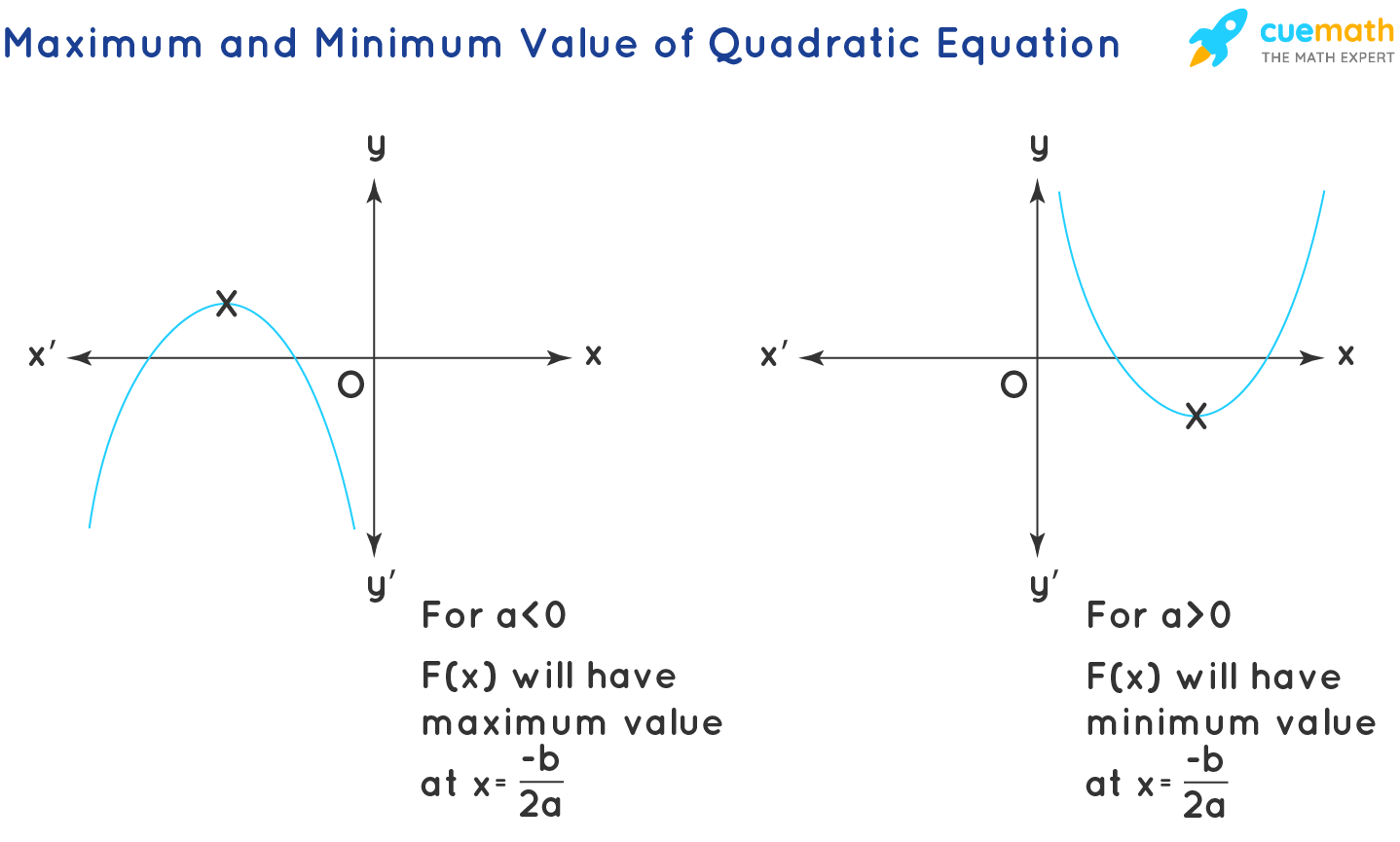
The maximum and minimum values of the quadratic expressions are of further help to find the range of the quadratic expression: The range of the quadratic expressions also depends on the value of a. For positive values of a( a > 0), the range is [ F(-b/2a), ∞), and for negative values of a ( a < 0), the range is (-∞, F(-b/2a)].
- For a > 0, Range: [ f(-b/2a), ∞)
- For a < 0, Range: (-∞, f(-b/2a)]
Note that the domain of a quadratic function is the set of all real numbers, i.e., (-∞, ∞).
Tips and Tricks on Quadratic Equation:
Some of the below-given tips and tricks on quadratic equations are helpful to more easily solve quadratic equations.
- The quadratic equations are generally solved through factorization. But in instances when it cannot be solved by factorization, the quadratic formula is used.
- The roots of a quadratic equation are also called the zeroes of the equation.
- For quadratic equations having negative discriminant values, the roots are represented by complex numbers.
- The sum and product of the roots of a quadratic equation can be used to find higher algebraic expressions involving these roots.
☛Related Topics:
- Roots Calculator
- Quadratic Factoring Calculator
- Roots of Quadratic Equation Calculator
Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.
Quadratic Equations Examples
Example 1: James is a fitness enthusiast and goes for a jog every morning. The park where he jogs is rectangular in shape and measures 12m × 8m. An environmentalist group plans to revamp the park and decides to build a pathway surrounding the park. This would increase the total area to 140 sq m. What will be the width of the pathway?
Let’s denote the width of the pathway by x.
Then, the length and breadth of the outer rectangle is (12+2x) m and (8+2x) m.
Given that, area = 140
(12 + 2x)(8 + 2x) = 140
2(6 + x) 2(4 + x) = 140
(6 + x)(4 + x) = 35
24 + 6x + 4x + x 2 = 35
x 2 + 10x -11 = 0
x 2 + 11x - x - 11 = 0
x(x + 11) - 1(x + 11) = 0
(x + 11)(x - 1) = 0
(x + 11) =0 and (x - 1) = 0
x = -11 and x = 1
Since length can’t be negative, we take x = 1.
Answer: Therefore the width of the pathway is 1 m.
Example 2: Rita throws a ball upwards from a platform that is 20m above the ground. The height of the ball from the ground at a time 't', is denoted by 'h'. Suppose h = -4t 2 + 16t + 20. Find the maximum height attained by the ball.
We can rearrange the terms of the quadratic equation
h = -4t 2 + 16t + 20
in such a way that it is easy to find the maximum value of this equation.
= -4t 2 + 16t + 20
= -4(t 2 - 4t - 5)
= -4((t - 2) 2 - 9)
= -4(t - 2) 2 + 36
We should keep the value of (t - 2) 2 minimum in order to find the maximum value of h.
So, the minimum value (t - 2) 2 can take is 0.
Answer: Therefore the maximum height attained is 36m.
Example 3: Find the quadratic equation having the roots 5 and 8 respectively.
The quadratic equation having the roots α, β, is x 2 - (α + β)x + αβ = 0.
Given α = 5, and β = 8.
Therefore the quadratic equation is:
x 2 - (5 + 8)x + 5×8 = 0
x 2 - 13x + 40 = 0
Answer: Hence the required quadratic equation is x 2 - 13x + 40 = 0
Example 4: The quad equation 2x 2 + 9x + 7 = 0 has roots α, β. Find the quadratic equation having the roots 1/α, and 1/β.
The quadratic equation having roots that are reciprocal to the roots of the equation ax 2 + bx + c = 0, is cx 2 + bx + a = 0.
The given quadratic equation is 2x 2 + 9x + 7 = 0.
Hence the required equation having reciprocal roots is 7x 2 + 9x + 2 = 0.
Method 2: From the given equation,
α + β = -9/2 and α β = 2/7.
The new equation should have its roots to be 1/α and 1/β.
Their sum = 1/α + 1/β = (α + β) / α β = -9/7 Their product = 1/α β = 2/7 Thus, the required equation is, x 2 - (1/α + 1/β)x + 1/α β = 0 x 2 - (-9/7)x + 2/7 = 0 Multiplying both sides by 7, 7x 2 + 9x + 2 = 0
Answer: Therefore the equation is 7x 2 + 9x + 2 = 0.
go to slide go to slide go to slide go to slide

Book a Free Trial Class
Practice Questions on Quadratic Equation
go to slide go to slide
FAQs on Quadratic Equation
What is the definition of a quadratic equation.
A quadratic equation in math is a second-degree equation of the form ax 2 + bx + c = 0. Here a and b are the coefficients, c is the constant term, and x is the variable. Since the variable x is of the second degree, there are two roots or answers for this quadratic equation. The roots of the quadratic equation can be found by either solving by factorizing or through the use of the quadratic formula.
What is the Quadratic Formula?
The quadratic equation formula to solve the equation ax 2 + bx + c = 0 is x = [-b ± √(b 2 - 4ac)]/2a. Here we obtain the two values of x, by applying the plus and minus symbols in this formula. Hence the two possible values of x are [-b + √(b 2 - 4ac)]/2a, and [-b - √(b 2 - 4ac)]/2a.
How do You Solve a Quadratic Equation?
There are several methods to solve quadratic equations, but the most common ones are factoring, using the quadratic formula, and completing the square.
- Factoring involves finding two numbers that multiply to equal the constant term, c, and add up to the coefficient of x, b.
- The quadratic formula is used when factoring is not possible, and it is given by x = [-b ± √(b 2 - 4ac)]/2a.
- Completing the square involves rewriting the quadratic equation in a different form that allows you to easily solve for x.
What is Determinant in Quadratic Formula?
The value b 2 - 4ac is called the discriminant and is designated as D. The discriminant is part of the quadratic formula. The discriminants help us to find the nature of the roots of the quadratic equation, without actually finding the roots of the quadratic equation.
What are Some Real-Life Applications of Quadratic Equations?
Quadratic equations are used to find the zeroes of the parabola and its axis of symmetry . There are many real-world applications of quadratic equations.
- They can be used in running time problems to evaluate the speed, distance or time while traveling by car, train or plane.
- Quadratic equations describe the relationship between quantity and the price of a commodity.
- Similarly, demand and cost calculations are also considered quadratic equation problems.
- It can also be noted that a satellite dish or a reflecting telescope has a shape that is defined by a quadratic equation.
How are Quadratic Equations Different From Linear Equations?
A linear degree is an equation of a single degree and one variable, and a quadratic equation is an equation in two degrees and a single variable. A linear equation is of the the form ax + b = 0 and a quadratic equation is of the form ax 2 + bx + c = 0. A linear equation has a single root and a quadratic equation has two roots or two answers. Also, a quadratic equation is a product of two linear equations.
What Are the 4 Ways To Solve A Quadratic Equation?
The four ways of solving a quadratic equation are as follows.
- Factorizing method
- Roots of Quadratic Equation Formula Method
- Method of Completing Squares
- Graphing Method
How to Solve a Quadratic Equation by Completing the Square?
The quadratic equation is solved by the method of completing the square and it uses the formula (a + b)^2 = a 2 + 2ab + b 2 (or) (a - b)^2 = a 2 - 2ab + b 2 .
How to Find the Value of the Discriminant?
The value of the discriminant in a quadratic equation can be found from the variables and constant terms of the standard form of the quadratic equation ax 2 + bx + c = 0. The value of the discriminant is D = b 2 - 4ac, and it helps to predict the nature of roots of the quadratic equation, without actually finding the roots of the equation.
How Do You Solve Quadratic Equations With Graphing?
The quadratic equation can be solved similarly to a linear equal by graphing. Let us take the quadratic equation ax 2 + bx + c = 0 as y = ax 2 + bx + c . Here we take the set of values of x and y and plot the graph. The two points where this graph meets the x-axis, are the solutions of this quadratic equation.
How Important Is the Discriminant of a Quadratic Equation?
The discriminant is very much needed to easily find the nature of the roots of the quadratic equation. Without the discriminant, finding the nature of the roots of the equation is a long process, as we first need to solve the equation to find both the roots. Hence the discriminant is an important and needed quantity, which helps to easily find the nature of the roots of the quadratic equation.
Where Can I Find Quadratic Equation Solver?
To get the quadratic equation solver, click here . Here, we can enter the values of a, b, and c for the quadratic equation ax 2 + bx + c = 0, then it will give you the roots along with a step-by-step procedure.
What is the Use of Discriminants in Quadratic Formula?
The discriminant (D = b 2 - 4ac) is useful to predict the nature of the roots of the quadratic equation. For D > 0, the roots are real and distinct, for D = 0 the roots are real and equal, and for D < 0, the roots do not exist or the roots are imaginary complex numbers . With the help of this discriminant and with the least calculations, we can find the nature of the roots of the quadratic equation.
How do you Solve a Quadratic Equation without Using the Quadratic Formula?
There are two alternative methods to the quadratic formula. One method is to solve the quadratic equation through factorization, and another method is by completing the squares. In total there are three methods to find the roots of a quadratic equation.
How to Derive Quadratic Formula?
The algebra formula (a + b) 2 = a 2 + 2ab + b 2 is used to solve the quadratic equation and derive the quadratic formula. This algebraic formula is used to manipulate the quadratic equation and derive the quadratic formula to find the roots of the equation.
Quadratic Equation Solver
What do you want to calculate.
- Solve for Variable
- Practice Mode
- Step-By-Step
Step-By-Step Example
Example (click to try), choose your method, solve by factoring.
Example: 3x^2-2x-1=0
Complete The Square
Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.)
Take the Square Root
Example: 2x^2=18
Quadratic Formula
Example: 4x^2-2x-1=0
About quadratic equations
Need more problem types? Try MathPapa Algebra Calculator
Clear Quadratic Equation Solver »
- Math Lessons
- Math Formulas
- Calculators
Math Calculators, Lessons and Formulas
It is time to solve your math problem
- HW Help (paid service)
- Solving Equations
- Quadratic Equation Solver
Quadratic equation solver
This step-by-step calculator solves quadratic equations using three different methods: the quadratic formula method , completing the square , and the factoring method . Calculator shows all the work and provides detailed explanation on how to solve an equation.
| Factoring |
| Completing the square |
| Quadratic formula |
- Factoring Polynomials
- Polynomial Roots
- Synthetic Division
- Polynomial Operations
- Graphing Polynomials
- Simplify Polynomials
- Generate From Roots
- Simplify Expression
- Multiplication / Division
- Addition / Subtraction
- Rationalize Denominator
- Simplifying
- Quadratic Equations Solver
- Polynomial Equations
- Solving Equations - With Steps
- Solving (with steps)
- Quadratic Plotter
- Factoring Trinomials
- Equilateral Triangle
- Right Triangle
- Oblique Triangle
- Square Calculator
- Rectangle Calculator
- Circle Calculator
- Hexagon Calculator
- Rhombus Calculator
- Trapezoid Calculator
- Triangular Prism
- Distance calculator
- Midpoint Calculator
- Triangle Calculator
- Graphing Lines
- Lines Intersection
- Two Point Form
- Line-Point Distance
- Parallel/Perpendicular
- Circle Equation
- Circle From 3 Points
- Circle-line Intersection
- Modulus, inverse, polar form
- Vectors (2D & 3D)
- Add, Subtract, Multiply
- Determinant Calculator
- Matrix Inverse
- Characteristic Polynomial
- Eigenvalues
- Eigenvectors
- Matrix Decomposition
- Limit Calculator
- Derivative Calculator
- Integral Calculator
- Arithmetic Sequences
- Geometric Sequences
- Find n th Term
- Degrees to Radians
- Trig. Equations
- Long Division
- Evaluate Expressions
- Fraction Calculator
- Greatest Common Divisor GCD
- Least Common Multiple LCM
- Prime Factorization
- Scientific Notation
- Percentage Calculator
- Dec / Bin / Hex
- Probability Calculator
- Probability Distributions
- Descriptive Statistics
- Standard Deviation
- Z - score Calculator
- Normal Distribution
- T-Test Calculator
- Correlation & Regression
- Simple Interest
- Compound Interest
- Amortization Calculator
- Annuity Calculator
- Work Problems
Hire MATHPORTAL experts to do math homework for you.
Prices start at $3 per problem.
How to use this calculator
The most commonly used methods for solving quadratic equations are:
1 . Factoring method
2 . Solving quadratic equations by completing the square
3 . Using quadratic formula
In the following sections, we'll go over these methods.
Method 1A : Factoring method
If a quadratic trinomial can be factored, this is the best solving method.
We often use this method when the leading coefficient is equal to 1 or -1. If this is not the case, then it is better to use some other method.
Example 01: Solve $ x^2 \color{red}{-8}x \color{blue}{+ 15} = 0 $ by factoring.
Here we see that the leading coefficient is 1, so the factoring method is our first choice.
To factor this equation, we must find two numbers ( $ a $ and $ b $ ) with a sum is $ a + b = \color{red}{8} $ and a product of $ a \cdot b = \color{blue}{15} $.
After some trials and errors, we see that $ a = 3 $ and $ b = 5 $.
Now we use formula $ x^2 - 8x + 15 = (x - a)(x - b) $ to get factored form:
Divide the factored form into two linear equations to get solutions.
Method 1B : Factoring - special cases
Example 02: Solve $ x^2 -8x = 0 $ by factoring.
In this case, (when the coefficient c = 0 ) we can factor out $ \color{blue}{x} $ out of $ x^2 - 8x $.
Example 03: Solve $ x^2 - 16 = 0 $ by factoring.
In this case, ( when the middle term is equal 0) we can use the difference of squares formula.
Method 3 : Solve using quadratic formula
This method solves all types of quadratic equations. It works best when solutions contain some radicals or complex numbers.
Example 05: Solve equation $ 2x^2 + 3x - 2 = 0$ by using quadratic formula.
Step 1 : Read the values of $a$, $b$, and $c$ from the quadratic equation. ( $a$ is the number in front of $x^2$ , $b$ is the number in front of $x$ and $c$ is the number at the end)
Step 2 :Plug the values for a, b, and c into the quadratic formula and simplify.
Step 3 : Solve for $x_1$ and $x_2$
Method 2 : Completing the square
This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. The method involves seven steps.
Example 04: Solve equation $ 2x^2 + 8x - 10= 0$ by completing the square.
Step 1 : Divide the equation by the number in front of the square term.
Step 2 : move $-5$ to the right:
Step 3 : Take half of the x-term coefficient $ \color{blue}{\dfrac{4}{2}} $, square it $ \color{blue}{\left(\dfrac{4}{2} \right)^2} $ and add this value to both sides.
Step 4 : Simplify left and right side.
Step 5 : Write the perfect square on the left.
Step 6 : Take the square root of both sides.
Step 7 : Solve for $x_1$ and $x_2$ .
1. Quadratic Equation — step-by-step examples, video tutorials with worked examples.
2. Completing the Square — video on Khan Academy
3. Completing the Square — video on Khan Academy
4. Polynomial equation solver
Welcome to MathPortal. This website's owner is mathematician Miloš Petrović. I designed this website and wrote all the calculators, lessons, and formulas .
If you want to contact me, probably have some questions, write me using the contact form or email me on [email protected]
Email (optional)

Go Green With Knowledge! Get 30% off on Annual Courses For World Environment Day with code NATURE30

Share this article

Table of Contents
Latest updates.

Ways To Improve Learning Outcomes: Learn Tips & Tricks

The Three States of Matter: Solids, Liquids, and Gases

Types of Motion: Introduction, Parameters, Examples

Understanding Frequency Polygon: Detailed Explanation

Uses of Silica Gel in Packaging?

Visual Learning Style for Students: Pros and Cons

Air Pollution: Know the Causes, Effects & More

Sexual Reproduction in Flowering Plants

Integers Introduction: Check Detailed Explanation

Human Respiratory System – Detailed Explanation
Tag cloud :.
- entrance exams
- engineering
- ssc cgl 2024
- Written By Madhurima Das
- Last Modified 14-11-2022
Methods of Solving Quadratic Equations: Formula, Methods, Examples
In algebra, polynomials are algebraic expressions with exponents of the variables as whole numbers. When a polynomial is equated to zero, we get a polynomial equation. If a quadratic polynomial is equated to zero, then we can call it a quadratic equation. A quadratic equation is an equation of second degree.
A quadratic equation makes a \( \cup \)-shaped curve (parabola) if we represent it graphically. There are always two solutions to a quadratic equation with either real roots or imaginary roots. Let us learn in detail the different methods of solving quadratic equations.
Definition of Quadratic Equations
An equation of second-degree polynomial in one variable, such as \(x\) usually equated to zero, is called a quadratic equation. The coefficient of \({x^2}\) must not be zero in a quadratic equation. \(p(x)\) is a quadratic polynomial, then \(p(x) = 0\) called a quadratic equation. For example, \(3{x^2} + 2x + 2 = 0, – {x^2} + 6x + 1 = 0,7{x^2} – 6x + 4 = 0\)etc., are quadratic equations.
Standard Form of a Quadratic Equation
The standard form of a quadratic equation is given by \(a{x^2} + bx + c = 0\) where\(a,b,c\) are real numbers, \(a \ne 0\) and \(a\) is the coefficient of \({x^2},b\) is the coefficient of \(x\) and \(c\) is a constant.
Roots of Quadratic Equations
The values of the variable, like \(x\) that satisfy the equation in one variable are called the roots of the equation. The roots of the quadratic equation may be real or imaginary.
If a quadratic polynomial is equated to zero, it becomes a quadratic equation. The values of \(x\) satisfying the equation are known as the roots of the quadratic equation. Note that the zeroes of the quadratic polynomial \(a{x^2} + bx + c\) and the roots of the quadratic equation \(a{x^2} + bx + c = 0\) are the same.
Methods to Solve the Quadratic Equations
There are some methods to solve the quadratic equation. They are,
1. Factorization method 2. Completing square method 3. Formula method 4. Graphical Method
Solving Quadratic Equation by Factorization Method
If we can factorize \(a{x^2} + bx + c,\,a \ne 0,\) into a product of two linear factors, then the roots of the quadratic equation \(a{x^2} + bx + c = 0\) can be found by equating each factor to zero.

Steps to Solve Quadratic Equation Using Factorization
If we can factorize \(a{x^2} + bx + c = 0,\,a \ne 0,\) into a product of two linear factors, then the roots of the quadratic equation \(a{x^2} + bx + c = 0\) can be found by equating each factor to zero.
Let us take an example and discuss it.
Consider a quadratic equation \({x^2} + 5x + 6 = 0.\)
1. Compare the given quadratic equation with the standard form \(a{x^2} + bx + c = 0\) and find the coefficients of \({x^2},x\) and the constant to get the values for \(a,b,c.\)
So, comparing \({x^2} + 5x + 6 = 0\) with \(a{x^2} + bx + c = 0\) we get, \(a = 1,b = 5,c = 6.\)
2. Now we will split \(b\) as the sum of two numbers such that the product of these two numbers \( = a \times c = ac\) We can factorize a quadratic equation when \(b\) can be split in \(v\) and \(w\) or \(b = v + w\) and \( = a\, \times c = ac.\)
So, \({x^2} + 5x + 6 = 0 \Rightarrow {x^2} + (2 + 3)x + 6 = 0 \Rightarrow {x^2} + 2x + 3x + 6 = 0.\)
3. Find the common factor of the first two and last two terms separately, such as the new two terms have the same common factor. So, \(x\) the common factor of the first two terms \({x^2} + 2x.\) Therefore, taking \(x\) outside, we get \({x^2} + 2x = x(x + 2).\)
\(3\) is the common factor of the last two terms \(3x + 6.\) Therefore, taking \(3\) outside, we get \(3x+6=3(x+2).\)
So, \({x^2} + 2x + 3x + 6 = 0\) can be written as \(x(x + 2) + 3(x + 2) = 0.\)
4. If we take out the same common factor, then we get the product of two linear polynomials. Here, we can see that \((x + 2)\) is the common factor in the new two terms. So, we can write \(x(x + 2) + 3(x + 2) = 0\,as\,(x + 2)(x + 3) = 0\) 5. At last, we will use the zero product rule to find the zeros. Zero product property says that when \(p \times q = 0\) then either \(p = 0\,or\,q = 0\) Therefore, \((x + 2) = 0,or(x + 3) = 0.\)
6. Hence, the solutions or roots of the quadratic equation \({x^2} + 5x + 6 = 0\) are \(x = – 2,x = – 3.\)
Solving Quadratic Equation by Completing the Square Method
A quadratic equation can be solved by the method of completing the square.
Steps to Solve Quadratic Equation by Completing the Square Method
Consider the quadratic equation, \(a{x^2} + bx + c = 0,a \ne 0\). Let us divide the equation by \(a\). \({x^2} + \frac{b}{a}x + \frac{c}{a} = 0\) Multiply and divide \(2\) to \(x\) term. \( \Rightarrow {x^2} + 2 \times \frac{b}{{2a}} \times x + \frac{c}{a} = 0\)
Now, to make the perfect square, we need to add and subtract \({\left( {\frac{b}{{2a}}} \right)^2}\) from L.H.S. \( \Rightarrow {x^2} + 2 \times \frac{b}{{2a}} \times x + {\left( {\frac{b}{{2a}}} \right)^2} – {\left( {\frac{b}{{2a}}} \right)^2} + \frac{c}{a} = 0\) \( \Rightarrow {\left( {x + \frac{b}{{2a}}} \right)^2} – {\left( {\frac{b}{{2a}}} \right)^2} + \frac{c}{a} = 0\)
Transferring \( – {\left( {\frac{b}{{2a}}} \right)^2} + \frac{c}{a}\) from \(L.H.S\) to \(R.H.S\) we have, \( \Rightarrow {\left( {x + \frac{b}{{2a}}} \right)^2} = – \frac{c}{a} + {\left( {\frac{b}{{2a}}} \right)^2}\)
Taking square root on both sides we have, \( \Rightarrow x + \frac{b}{{2a}} = \pm \sqrt { – \frac{c}{a} + {{\left( {\frac{b}{{2a}}} \right)}^2}} \) \( \Rightarrow x = \pm \sqrt { – \frac{c}{a} + {{\left( {\frac{b}{{2a}}} \right)}^2}} – \frac{b}{{2a}}\)
For example, consider the quadratic equation \(2{x^2} + 8x + 3 = 0\)
Let us divide the equation by \(a\, = \,2\) \(2\left( {{x^2} + \frac{8}{2}x + \frac{3}{2}} \right) = 0\) \( \Rightarrow {x^2} + 4x + \frac{3}{2} = 0\) \( \Rightarrow {x^2} + 2 \times 2x + \frac{3}{2} = 0\)
Now, to make the perfect square, we need to add and subtract \({(2)^2}\) from \(L.H.S.\) \( \Rightarrow {x^2} + 2 \times 2 \times x + {(2)^2} – {(2)^2} + \frac{3}{2} = 0\) \( \Rightarrow {(x + 2)^2} – {(2)^2} + \frac{3}{2} = 0\)
Transferring \( – {(2)^2} + \frac{3}{2}\) from \(L.H.S\,to\,R.H.S\) we have, \( \Rightarrow {(x + 2)^2} = {(2)^2} – \frac{3}{2}\)
Taking square root on both sides we have, \( \Rightarrow x + 2 = \pm \sqrt {4 – \frac{3}{2}} \) \( \Rightarrow x = \pm \sqrt {\frac{5}{2}} – 2\)
Hence, the required solution of the quadratic equation \(2{x^2} + 8x + 3 = 0\) is \(x = \pm \sqrt {\frac{5}{2}} – 2\)
Solving Quadratic Equation by Formula Method
The roots of the quadratic equation \(a{x^2} + bx + c = 0\) are given by the quadratic formula
\(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\)
For example, consider the quadratic equation \(3{x^2} – 5x + 2 = 0\)
From the given quadratic equation \(a = 3,\,b = – 5,\,c = 2\)
The quadratic Equation formula is given by
\(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\) \(x = \frac{{ – ( – 5) \pm \sqrt {{{( – 5)}^2} – 4 \times 3 \times 2} }}{{2a}} = \frac{{ + 5 \pm \sqrt {25 – 24} }}{6}\) \( = x = \frac{{ – ( – 5) \pm \sqrt {{{( – 5)}^2} – 4 \times 3 \times 2} }}{{2 \times 3}} = \frac{{5 \pm \sqrt {25 – 24} }}{6}\) \( = \frac{{5 \pm \sqrt 1 }}{6} = \frac{{5 \pm 1}}{6} = \frac{{5 + 1}}{6},\frac{{5 – 1}}{6} = \frac{6}{6},\frac{4}{6}\) \( \Rightarrow x = 1\) or \(x = \frac{2}{3}\)
Hence, the roots of the given quadratic equation are \( \Rightarrow x = 1\) or \(x = \frac{2}{3}\)
Graphical Solution of Quadratic Equation
The standard form of a quadratic equation is \(a{x^2} + bx + c = 0,\) where \(a,b\) and \(c\) are real and \(a\,\, \ne \,\,0\)
Let us take an example and discuss \({x^2} – 5x + 6 = 0\) Considering \(p(x) = {x^2} – 5x + 6\) A quadratic polynomial always gives a parabolic graph. In a polynomial, the value of \(x\) which is responsible to make \(p(x) = 0\) is called the zero of the polynomial. When the polynomial equated with zero, it becomes an equation. If the zeros of the quadratic polynomial are known then they can be considered as the solutions of the equation which is formed by equating the polynomial to zero.
When \(x = + 2,p(2) = {(2)^2} – 5(2) + 6 = 4 – 10 + 6 = – 6 + 6 = 0\) \(x = + 3,p(3) = {(3)^2} – 5(3) + 6 = 9 – 15 + 6 = – 6 + 6 = 0\) Hence, the zeros of the quadratic polynomial are \( + 3,\, + 2\) If we represent the polynomial graphically then, the graph of the polynomial cuts the \(x – \)axis at \( + 3\,{\rm{and}}\, + 2\)

Let us take another example and discuss \({x^2} – 2x + 1 = 0\). Considering \(p(x) = {x^2} – 2x + 1\) A quadratic polynomial always gives a parabolic graph. When \(x = + 1,p(1) = {(1)^2} – 2(1) + 1 = 1 – 2 + 1 = – 1 + 1 = 0\) Hence, the zeros of the polynomial are \( + 1\) If we represent the polynomial graphically then, the graph of the polynomial touches the \(x – \)axis at \( + 1\). Therefore, the solution of the equation is \( + 1\).

Solved Examples
Q.1. Find the roots of the quadratic equation \(6{x^2} – x – 2 = 0\) Ans: We have \(6{x^2} – x – 2 = 0\) \( \Rightarrow 6{x^2} + 3x – 4x – 2 = 0\) \( \Rightarrow 3x(2x + 1) – 2(2x + 1) = 0\) The roots of \(6{x^2} – x – 2 = 0\) are the values of \(x\) for which \((3x – 2)(2x + 1) = 0\) Therefore, \(3x – 2 = 0\,\,or\,2x\,\, + \,\,1 = 0\) \(x = \frac{2}{3},x = \frac{{ – 1}}{2}\) Hence, the roots are \(\frac{2}{3}\& \frac{{ – 1}}{2}.\)
Q.2. Find the roots of the quadratic equation by using the formula method \(2{x^2} – 8x – 24 = 0\) Ans: From the given quadratic equation \(a = 2,b = – 8,c = – 24\) Quadratic equation formula is given by \(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\) \(x = \frac{{ – ( – 8) \pm \sqrt {{{( – 8)}^2} – 4 \times 2 \times ( – 24)} }}{{2 \times 2}} = \frac{{8 \pm \sqrt {64 + 192} }}{4}\) \(x = \,\frac{{8 \pm \sqrt {256} }}{4}S = \frac{{8 \pm 16}}{4} = \frac{{8 + 16}}{4},\frac{{8 – 16}}{4} = \frac{{24}}{4},\frac{{ – 8}}{4}\) \( \Rightarrow x = 6,x = – 2\) Hence, the roots of the given quadratic equation are \(6\& – 2.\)
Q.3. Find the roots of the quadratic equation \({x^2} + 10x + 21 = 0\) by completing the square method. Ans: \({x^2} + 10x + 21 = 0\) \( \Rightarrow {x^2} + 10x = – 21\) (Subtracted \(21\) from both sides of the equation) \( \Rightarrow {x^2} + 10x + 25 = – 21 + 25\) (Added \({\left( {\frac{b}{2}} \right)^2} = {\left( {\frac{{10}}{2}} \right)^2} = 25\) on both the sides of the equation) \( \Rightarrow {(x + 5)^2} = 4\) (Completed the square by using the identity \({(a + b)^2} = {a^2} + 2ab + {b^2}\)) Then, take the square root on both sides. \(x + 5 = \pm 2\) \(x = – 3,x = – 7\) Hence, the roots of the given quadratic equation are \( – 3\& – 7.\)
Q.4. Find the roots of the quadratic equation\(2{x^2} + 8x + 3 = 0\) by completing the square method. Ans: \( \Rightarrow 2{x^2} + 8x = – 3\) [Subtracted \(3\) from both sides of the equation] \( \Rightarrow {x^2} + 4x = \frac{{ – 3}}{2}\) (Divided both sides of the equation by \(2\)) \( \Rightarrow {x^2} + 4x+4 = \frac{{ – 3}}{2} + 4\) [Added \({\left( {\frac{b}{2}} \right)^2} = {\left( {\frac{4}{2}} \right)^2} = 4\) on both the sides of the equation] \(\Rightarrow(x+2)^{2}=\frac{5}{2}\) [Completed the square by using the identity \((a+b)^{2}=a^{2}+2 a b+b^{2}\)] Then, take the square root on both the sides \( \Rightarrow x + 2 = \pm \sqrt {\frac{5}{2}} \) \( \Rightarrow x = -2 \pm \sqrt {\frac{5}{2}} \) is the required solutions.
Q.5. Find the roots of the quadratic equation \({x^2} + 3x – 10 = 0\) by factorization method. Ans: We have \({x^2} + 3x – 10 = 0\) \( \Rightarrow {x^2} + 5x – 2x – 10 = 0\) \( \Rightarrow x(x + 5) – 2(x + 5) = 0\) \( \Rightarrow (x – 2)(x + 5) = 0\) So, the roots of \({x^2} + 3x – 10 = 0\) are the values of \(x\) for which \((x – 2)(x + 5) = 0\) Therefore, \(x – 2 = 0\,\,or\,x + 5 = 0\) \(x = 2, – 5\,\) Hence, the roots are \(2\& – 5.\)
In this article, we discussed quadratic equation in the variable \(x\) which is an equation of the form \(a{x^2} + bx + c = 0,\) where \(a,b,c\) are real numbers, \(a\, \ne 0\) Also, we discussed the methods of solving the quadratic equations such as factorizing method, completing the square method, formula method etc.
FAQs on Methods of Solving Quadratic Equations
Q.1. What are \(5\) methods of solving a quadratic equation? Ans: We can solve the quadratic equations by using different methods given below: 1. By factorizing method 2. By completing the square method 3. By using the quadratic formula 4. By using the graphical method 5. By using the trial and error method
Q.2. How can you identify a quadratic equation? Ans: An equation is a quadratic equation in the variable \(x\) if it is of the form \(a{x^2} + bx + c = 0\) where \(a,b,c\) are real numbers, \(a\, \ne \,0\).
Q.3. Which method can you use to solve all quadratic equations? Ans: We can not use factorizing method and completing square method for every quadratic equation as there are some constraints. We can use the formula method to solve all quadratic equations. The roots of the quadratic equation \(a{x^2} + bx + c = 0\) are given by: \(x = \frac{{ – b \pm \sqrt {{b^2} – 4ac} }}{{2a}}\) This is the quadratic formula for finding the roots of a quadratic equation.
Q.4. How many types of quadratic equations are there? Ans: There are three types of quadratic equations: 1. Standard form: \(a{x^2} + bx + c = 0,a \ne 0\) 2. Factored form: \((x – a)(x – b) = 0\) 3. Vertex form: \(a{(x – h)^2} + k = 0\) Each form of a quadratic equation has specific importance. Therefore, identifying the benefits of each different form can make it easier to understand and solve different situations.
Q.5. Can you use the quadratic formula for any quadratic equation? Ans: Yes, we can use the quadratic formula for any quadratic equation.
Q.6. What is the standard form of the quadratic equation? Ans: The form \(a{x^2} + bx + c = 0,\,a \ne 0\) is called the standard form of a quadratic equation.
We hope you find this detailed article on methods of solving quadratic equations helpful. If you have any doubts or queries regarding this topic, feel to ask us in the comment section.
Related Articles
Ways To Improve Learning Outcomes: With the development of technology, students may now rely on strategies to enhance learning outcomes. No matter how knowledgeable a...
The Three States of Matter: Anything with mass and occupied space is called ‘Matter’. Matters of different kinds surround us. There are some we can...
Motion is the change of a body's position or orientation over time. The motion of humans and animals illustrates how everything in the cosmos is...
Understanding Frequency Polygon: Students who are struggling with understanding Frequency Polygon can check out the details here. A graphical representation of data distribution helps understand...
When you receive your order of clothes or leather shoes or silver jewellery from any online shoppe, you must have noticed a small packet containing...
Visual Learning Style: We as humans possess the power to remember those which we have caught visually in our memory and that too for a...
Air Pollution: In the past, the air we inhaled was pure and clean. But as industrialisation grows and the number of harmful chemicals in the...
In biology, flowering plants are known by the name angiosperms. Male and female reproductive organs can be found in the same plant in flowering plants....
Integers Introduction: To score well in the exam, students must check out the Integers introduction and understand them thoroughly. The collection of negative numbers and whole...
Human Respiratory System: Students preparing for the NEET and Biology-related exams must have an idea about the human respiratory system. It is a network of tissues...
Place Value of Numbers: Detailed Explanation
Place Value of Numbers: Students must understand the concept of the place value of numbers to score high in the exam. In mathematics, place value...
The Leaf: Types, Structures, Parts
The Leaf: Students who want to understand everything about the leaf can check out the detailed explanation provided by Embibe experts. Plants have a crucial role...
Factors Affecting Respiration: Definition, Diagrams with Examples
In plants, respiration can be regarded as the reversal of the photosynthetic process. Like photosynthesis, respiration involves gas exchange with the environment. Unlike photosynthesis, respiration...
General Terms Related to Spherical Mirrors
General terms related to spherical mirrors: A mirror with the shape of a portion cut out of a spherical surface or substance is known as a...
Number System: Types, Conversion and Properties
Number System: Numbers are highly significant and play an essential role in Mathematics that will come up in further classes. In lower grades, we learned how...
Types of Respiration
Every living organism has to "breathe" to survive. The process by which the living organisms use their food to get energy is called respiration. It...
Animal Cell: Definition, Diagram, Types of Animal Cells
Animal Cell: An animal cell is a eukaryotic cell with membrane-bound cell organelles without a cell wall. We all know that the cell is the fundamental...
Conversion of Percentages: Conversion Method & Examples
Conversion of Percentages: To differentiate and explain the size of quantities, the terms fractions and percent are used interchangeably. Some may find it difficult to...
Arc of a Circle: Definition, Properties, and Examples
Arc of a circle: A circle is the set of all points in the plane that are a fixed distance called the radius from a fixed point...
Ammonia (NH3): Preparation, Structure, Properties and Uses
Ammonia, a colourless gas with a distinct odour, is a chemical building block and a significant component in producing many everyday items. It is found...
CGPA to Percentage: Calculator for Conversion, Formula, & More
CGPA to Percentage: The average grade point of a student is calculated using their cumulative grades across all subjects, omitting any supplemental coursework. Many colleges,...
Uses of Ether – Properties, Nomenclature, Uses, Disadvantages
Uses of Ether: Ether is an organic compound containing an oxygen atom and an ether group connected to two alkyl/aryl groups. It is formed by the...
General and Middle Terms: Definitions, Formula, Independent Term, Examples
General and Middle terms: The binomial theorem helps us find the power of a binomial without going through the tedious multiplication process. Further, the use...
Mutually Exclusive Events: Definition, Formulas, Solved Examples
Mutually Exclusive Events: In the theory of probability, two events are said to be mutually exclusive events if they cannot occur simultaneously or at the...
Geometry: Definition, Shapes, Structure, Examples
Geometry is a branch of mathematics that is largely concerned with the forms and sizes of objects, their relative positions, and the qualities of space....
Bohr’s Model of Hydrogen Atom: Expressions for Radius, Energy
Rutherford’s Atom Model was undoubtedly a breakthrough in atomic studies. However, it was not wholly correct. The great Danish physicist Niels Bohr (1885–1962) made immediate...
Types of Functions: Definition, Classification and Examples
Types of Functions: Functions are the relation of any two sets. A relation describes the cartesian product of two sets. Cartesian products of two sets...

39 Insightful Publications

Embibe Is A Global Innovator

Innovator Of The Year Education Forever

Interpretable And Explainable AI

Revolutionizing Education Forever

Best AI Platform For Education

Enabling Teachers Everywhere

Decoding Performance

Leading AI Powered Learning Solution Provider

Auto Generation Of Tests

Disrupting Education In India

Problem Sequencing Using DKT

Help Students Ace India's Toughest Exams

Best Education AI Platform

Unlocking AI Through Saas

Fixing Student’s Behaviour With Data Analytics

Leveraging Intelligence To Deliver Results

Brave New World Of Applied AI

You Can Score Higher

Harnessing AI In Education

Personalized Ed-tech With AI

Exciting AI Platform, Personalizing Education

Disruptor Award For Maximum Business Impact

Top 20 AI Influencers In India

Proud Owner Of 9 Patents

Innovation in AR/VR/MR

Best Animated Frames Award 2024
Trending Searches
Previous year question papers, sample papers.
Reduce Silly Mistakes; Take Mock Tests related to Quadratic Reactions

Take Unlimited Mock Tests based on Quadratic Reactions
Enter mobile number.
By signing up, you agree to our Privacy Policy and Terms & Conditions
Quadratic Equations
An example of a Quadratic Equation :
The function can make nice curves like this one:
The name Quadratic comes from "quad" meaning square, because the variable gets squared (like x 2 ).
It is also called an "Equation of Degree 2" (because of the "2" on the x )
Standard Form
The Standard Form of a Quadratic Equation looks like this:
- a , b and c are known values. a can't be 0
- x is the variable or unknown (we don't know it yet)
Here are some examples:
| + 5x + 3 = 0 | In this one , and | |
| − 3x = 0 | This one is a little more tricky: ? Well , as we don't usually write "1x " ? Well , so is not shown. | |
| This one is a quadratic equation: it is missing (in other words , which means it can't be quadratic) |
Have a Play With It
Play with the Quadratic Equation Explorer so you can see:
- the function's graph, and
- the solutions (called "roots").
Hidden Quadratic Equations!
As we saw before, the Standard Form of a Quadratic Equation is
But sometimes a quadratic equation does not look like that!
For example:
| In disguise | In Standard Form | a, b and c | |
|---|---|---|---|
| = 3x − 1 | Move all terms to left hand side | − 3x + 1 = 0 | a=1, b=−3, c=1 |
| − 2w) = 5 | (undo the ), and move 5 to left | − 4w − 5 = 0 | a=2, b=−4, c=−5 |
| Expand, and move 3 to left | − z − 3 = 0 | a=1, b=−1, c=−3 |
How To Solve Them?
The " solutions " to the Quadratic Equation are where it is equal to zero .
They are also called " roots ", or sometimes " zeros "
There are usually 2 solutions (as shown in this graph).
And there are a few different ways to find the solutions:
Just plug in the values of a, b and c, and do the calculations.
We will look at this method in more detail now.
About the Quadratic Formula
First of all what is that plus/minus thing that looks like ± ?
The ± means there are TWO answers:
x = −b + √(b 2 − 4ac) 2a
x = −b − √(b 2 − 4ac) 2a
Here is an example with two answers:
But it does not always work out like that!
- Imagine if the curve "just touches" the x-axis.
- Or imagine the curve is so high it doesn't even cross the x-axis!
This is where the "Discriminant" helps us ...
Discriminant
Do you see b 2 − 4ac in the formula above? It is called the Discriminant , because it can "discriminate" between the possible types of answer:
- when b 2 − 4ac is positive, we get two Real solutions
- when it is zero we get just ONE real solution (both answers are the same)
- when it is negative we get a pair of Complex solutions
Complex solutions? Let's talk about them after we see how to use the formula.
Using the Quadratic Formula
Just put the values of a, b and c into the Quadratic Formula, and do the calculations.
Example: Solve 5x 2 + 6x + 1 = 0
Answer: x = −0.2 or x = −1
Let's check the answers:
Remembering The Formula
A kind reader suggested singing it to "Pop Goes the Weasel":
Try singing it a few times and it will get stuck in your head!
Or you can remember this story:
x = −b ± √(b 2 − 4ac) 2a
"A negative boy was thinking yes or no about going to a party, at the party he talked to a square boy but not to the 4 awesome chicks. It was all over at 2 am. "
Complex Solutions?
When the Discriminant (the value b 2 − 4ac ) is negative we get a pair of Complex solutions ... what does that mean?
It means our answer will include Imaginary Numbers . Wow!
Example: Solve 5x 2 + 2x + 1 = 0
Answer: x = −0.2 ± 0.4 i
The graph does not cross the x-axis. That is why we ended up with complex numbers.
In a way it is easier: we don't need more calculation, we leave it as −0.2 ± 0.4 i .
Example: Solve x 2 − 4x + 6.25 = 0
Answer: x = 2 ± 1.5 i
BUT an upside-down mirror image of our equation does cross the x-axis at 2 ± 1.5 (note: missing the i ).
Just an interesting fact for you!
- Quadratic Equation in Standard Form: ax 2 + bx + c = 0
- Quadratic Equations can be factored
- Quadratic Formula: x = −b ± √(b 2 − 4ac) 2a
- positive, there are 2 real solutions
- zero, there is one real solution
- negative, there are 2 complex solutions

The Quadratic Formula
What it is, what it does, and how to use it
What is the Quadratic Formula?
The quadratic formula is:

What does this formula tell us?
The quadratic formula calculates the solutions of any quadratic equation.
What is a quadratic equation?
A quadratic equation is an equation that can be written as ax ² + bx + c where a ≠ 0 . In other words, a quadratic equation must have a squared term as its highest power.
Examples of quadratic equations
$$ y = 5x^2 + 2x + 5 \\ y = 11x^2 + 22 \\ y = x^2 - 4x +5 \\ y = -x^2 + + 5 $$
Non Examples
$$ y = 11x + 22 \\ y = x^3 -x^2 +5x +5 \\ y = 2x^3 -4x^2 \\ y = -x^4 + 5 $$
Ok, but what is a 'solution'?
Well a solution can be thought in two ways:
| For any quadratic equation of the form f(x) = ax +bx+c, the solution is when f(x) = 0. | |
| The solution is where the graph of a quadratic equation (a ) is intersects the x-axis. This, of course, only applies to real solutions. |
Example of the quadratic formula to solve an equation
Use the formula to solve theQuadratic Equation: $$ y = x^2 + 2x + 1 $$ .
Just substitute a,b, and c into the general formula:
$$ a = 1 \\ b = 2 \\ c = 1 $$
Below is a picture representing the graph of y = x² + 2x + 1 and its solution.
Quadratic Formula Song
A catchy way to remember the quadratic formula is this song (pop goes the weasel).
Practice Problems
Use the quadratic formula to find the solutions to the following equation: y = x² − 2x + 1 and its solution.
- b = − 2
Use the quadratic formula to find the solutions to the following equation: y = x² − x − 2 and its solution .
In this quadratic equation, y = x² − x − 2 and its solution:
- b = − 1
- c = − 2
Use the quadratic formula to find the solutions to the following equation: y = x² − 1 and its solution.
In this quadratic equation, y = x² − 1 and its solution:
- c = −1
Calculate the solutions of the the quadratic equation below by using the quadratic formula : y = x² + 2x − 3 and its solution.
In this quadratic equation, y = x² + 2x − 3 and its solution:
- c = −3
Below is a picture of the graph of the quadratic equation and its two solutions.
Use the quadratic formula to find the solutions to the following equation: y = x² + 4x − 5 and its solution.
In this quadratic equation, y = x² + 4x − 5 and its solution:
- c = −5
Use the quadratic formula to find the solutions to the following equation: y = x² − 4x + 5 and its solution.
In this quadratic equation, y = x² − 4x + 5 and its solution:
- b = −4
Below is a picture of this quadratic's graph.
- Solving Quadratic Equations

- Discriminant
- Completing the Square in Math
Completing The Square Calculator
Solves Equation and lets you print image to Desktop!

- Quadratic Formula Calculator
- Formula for Sum and Product of Roots
Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!
Popular pages @ mathwarehouse.com.


Solving Quadratics by Square Root Method
How to solve quadratic equations using the square root method.
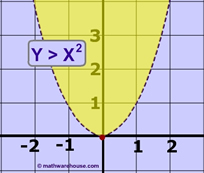
This is the “best” method whenever the quadratic equation only contains [latex]{x^2}[/latex] terms. That implies no presence of any [latex]x[/latex] term being raised to the first power somewhere in the equation.
The general approach is to collect all [latex]{x^2}[/latex] terms on one side of the equation while keeping the constants to the opposite side. After doing so, the next obvious step is to take the square roots of both sides to solve for the value of [latex]x[/latex]. Always attach the [latex] \pm [/latex] symbol when you get the square root of the constant.
Examples of How to Solve Quadratic Equations by Square Root Method
Example 1 : Solve the quadratic equation below using the Square Root Method.
I will isolate the only [latex]{x^2}[/latex] term on the left side by adding both sides by [latex] + 1[/latex]. Then solve the values of [latex]x[/latex] by taking the square roots of both sides of the equation. As I mentioned before, we need to attach the plus or minus symbol to the square root of the constant.
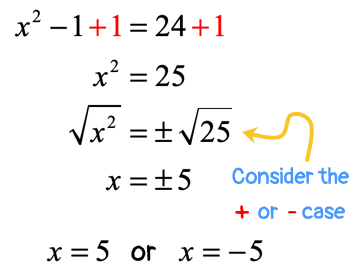
So I have [latex]x = 5[/latex] and [latex]x = – \,5[/latex] as final answers since both of these values satisfy the original quadratic equation. I will leave it to you to verify.
Example 2 : Solve the quadratic equation below using the Square Root Method.
This problem is very similar to the previous example. The only difference is that after I have separated the [latex]{x^2}[/latex] term and the constant in the opposite sides of the equation, I need to divide the equation by the coefficient of the squared term before taking the square roots of both sides.

The final answers are [latex]x = 4[/latex] and [latex]x = – \,4[/latex].
Example 3 : Solve the quadratic equation below using the Square Root Method.
I can see that I have two [latex]{x^2}[/latex] terms, one on each side of the equation. My approach is to collect all the squared terms of [latex]x[/latex] to the left side, and combine all the constants to the right side. Then solve for [latex]x[/latex] as usual, just like in Examples 1 and 2.
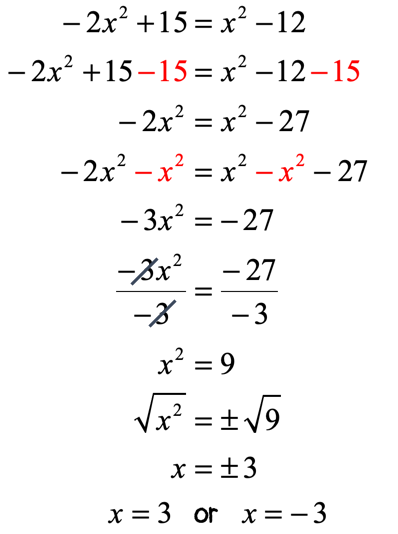
The solutions to this quadratic formula are [latex]x = 3[/latex] and [latex]x = – \,3[/latex].
Example 4 : Solve the quadratic equation below using the Square Root Method.
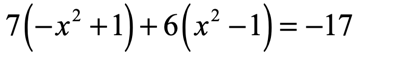
The two parentheses should not bother you at all. The fact remains that all variables come in the squared form, which is what we want. This problem is perfectly solvable using the square root method.
So my first step is to eliminate both of the parentheses by applying the distributive property of multiplication. Once they are gone, I can easily combine like terms. Keep the [latex]{x^2}[/latex] terms to the left, and constants to the right. Finally, apply square root operation in both sides and we’re done!
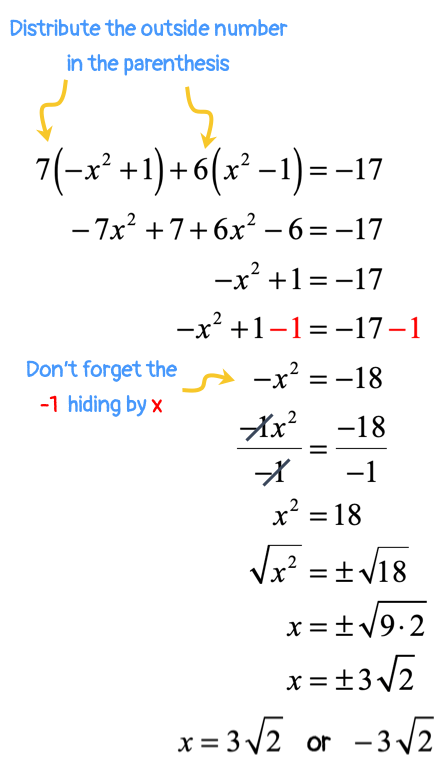
Not too bad, right?
Example 5 : Solve the quadratic equation below using the Square Root Method.
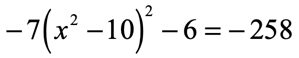
Since the [latex]x[/latex]-term is being raised to the second power twice, that means, I need to perform two square root operations in order to solve for [latex]x[/latex].
The first step is to have something like this: ( ) 2 = constant . This allows me to get rid of the exponent of the parenthesis on the first application of square root operation.
After doing so, what remains is the “stuff” inside the parenthesis which has an [latex]{x^2}[/latex] term. Well, this is great since I already know how to handle it just like the previous examples.

There’s an [latex]x[/latex]-squared term left after the first application of square root.
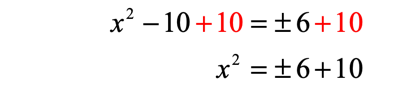
Now we have to break up [latex]{x^2} = \pm \,6 + 10[/latex] into two cases because of the “plus” or “minus” in [latex]6[/latex].
- Solve the first case where [latex]6[/latex] is positive .
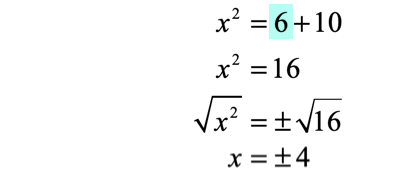
- Solve the second case where [latex]6[/latex] is negative .
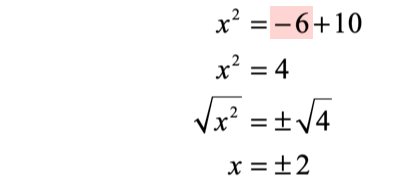
The solutions to this quadratic equations are [latex]x = 4[/latex], [latex]x = – \,4[/latex], [latex]x = 2[/latex], and [latex]x = – \,2[/latex]. Yes, we have four values of [latex]x[/latex] that can satisfy the original quadratic equation.
Example 6 : Solve the quadratic equation below using the Square Root Method.
Example 7 : Solve the quadratic equation below using the Square Root Method.
You may also be interested in these related math lessons or tutorials:
Solving Quadratic Equations by Factoring Method Solving Quadratic Equations by the Quadratic Formula Solving Quadratic Equations by Completing the Square
Quadratic Formula Calculator
Enter the equation you want to solve using the quadratic formula.
The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions.
Quadratic Formula : x = − b ± b 2 − 4 a c 2 a
Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator !
Solve Using the Quadratic Formula Apply the Quadratic Formula
Number Line
- quadratic\:formula\:-x^{2}+4x-3=0
- quadratic\:formula\:-r^{2}-r+2=0
- quadratic\:formula\:4x^{2}=4x-1
- quadratic\:formula\:3x^{2}=2x+5
quadratic-equation-solve-using-quadratic-formula-calculator
- High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...
Please add a message.
Message received. Thanks for the feedback.
- Math Article
Quadratics or Quadratic Equations

Quadratics can be defined as a polynomial equation of a second degree, which implies that it comprises a minimum of one term that is squared. It is also called quadratic equations . The general form of the quadratic equation is:
ax² + bx + c = 0
where x is an unknown variable and a, b, c are numerical coefficients. For example, x 2 + 2x +1 is a quadratic or quadratic equation. Here, a ≠ 0 because if it equals zero then the equation will not remain quadratic anymore and it will become a linear equation, such as:
Thus, this equation cannot be called a quadratic equation.
The terms a, b and c are also called quadratic coefficients.
The solutions to the quadratic equation are the values of the unknown variable x, which satisfy the equation. These solutions are called roots or zeros of quadratic equations . The roots of any polynomial are the solutions for the given equation.
What is Quadratic Equation?
The polynomial equation whose highest degree is two is called a quadratic equation or sometimes just quadratics. It is expressed in the form of:
where x is the unknown variable and a, b and c are the constant terms.
Standard Form of Quadratic Equation
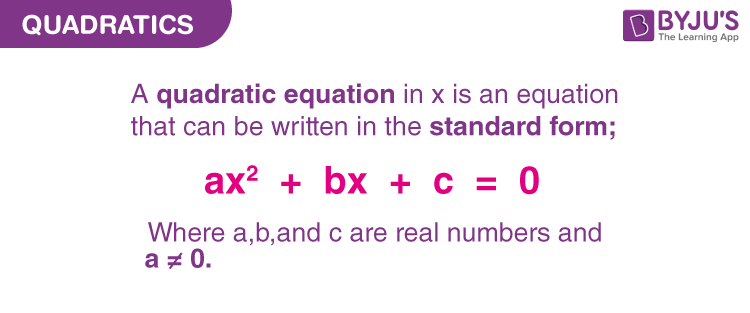
Since the quadratic includes only one unknown term or variable, thus it is called univariate. The power of variable x is always non-negative integers. Hence the equation is a polynomial equation with the highest power as 2.
The solution for this equation is the values of x, which are also called zeros. Zeros of the polynomial are the solution for which the equation is satisfied. In the case of quadratics, there are two roots or zeros of the equation. And if we put the values of roots or x on the left-hand side of the equation, it will equal to zero. Therefore, they are called zeros.
Quadratics Formula
The formula for a quadratic equation is used to find the roots of the equation. Since quadratics have a degree equal to two, therefore there will be two solutions for the equation. Suppose ax² + bx + c = 0 is the quadratic equation, then the formula to find the roots of this equation will be:
x = [-b±√(b 2 -4ac)]/2a
The sign of plus/minus indicates there will be two solutions for x. Learn in detail the quadratic formula here.
Examples of Quadratics
Beneath are the illustrations of quadratic equations of the form (ax² + bx + c = 0)
- x² –x – 9 = 0
- 5x² – 2x – 6 = 0
- 3x² + 4x + 8 = 0
- -x² +6x + 12 = 0
Examples of a quadratic equation with the absence of a ‘ C ‘- a constant term.
- -x² – 9x = 0
- x² + 2x = 0
- -6x² – 3x = 0
- -5x² + x = 0
- -12x² + 13x = 0
- 11x² – 27x = 0
Following are the examples of a quadratic equation in factored form
- (x – 6)(x + 1) = 0 [ result obtained after solving is x² – 5x – 6 = 0]
- –3(x – 4)(2x + 3) = 0 [result obtained after solving is -6x² + 15x + 36 = 0]
- (x − 5)(x + 3) = 0 [result obtained after solving is x² − 2x − 15 = 0]
- (x – 5)(x + 2) = 0 [ result obtained after solving is x² – 3x – 10 = 0]
- (x – 4)(x + 2) = 0 [result obtained after solving is x² – 2x – 8 = 0]
- (2x+3)(3x – 2) = 0 [result obtained after solving is 6x² + 5x – 6]
Below are the examples of a quadratic equation with an absence of linear co – efficient ‘ bx’
- 2x² – 64 = 0
- x² – 16 = 0
- 9x² + 49 = 0
- -2x² – 4 = 0
- 4x² + 81 = 0
- -x² – 9 = 0
How to Solve Quadratic Equations?
There are basically four methods of solving quadratic equations. They are:
- Completing the square
Using Quadratic Formula
- Taking the square root
Factoring of Quadratics
- Begin with a equation of the form ax² + bx + c = 0
- Ensure that it is set to adequate zero.
- Factor the left-hand side of the equation by assuming zero on the right-hand side of the equation.
- Assign each factor equal to zero.
- Now solve the equation in order to determine the values of x.
Suppose if the main coefficient is not equal to one then deliberately, you have to follow a methodology in the arrangement of the factors.
(2x+3)(x-2)=0
Learn more about the factorization of quadratic equations here.
Completing the Square Method
Let us learn this method with example.
Example: Solve 2x 2 – x – 1 = 0.
First, move the constant term to the other side of the equation.
2x 2 – x = 1
Dividing both sides by 2.
x 2 – x/2 = ½
Add the square of half of the coefficient of x, (b/2a) 2 , on both the sides, i.e., 1/16
x 2 – x/2 + 1/16 = ½ + 1/16
Now we can factor the right side,
(x-¼) 2 = 9/16 = (¾) 2
Taking root on both sides;
X – ¼ = ±3/4
Add ¼ on both sides
X = ¼ + ¾ = 4/4 = 1
X = ¼ – ¾ = -2/4 = -½
To learn more about completing the square method, click here .
For the given Quadratic equation of the form, ax² + bx + c = 0
Therefore the roots of the given equation can be found by:
\(\begin{array}{l}x = \frac{-b \pm \sqrt{b^{2}-4ac}}{2a}\end{array} \)
where ± (one plus and one minus) represent two distinct roots of the given equation.
Taking the Square Root
We can use this method for the equations such as:
x 2 + a 2 = 0
Example: Solve x 2 – 50 = 0.
x 2 – 50 = 0
Taking the roots both sides
√x 2 = ±√50
x = ±√(2 x 5 x 5)
Thus, we got the required solution.
Related Articles
Video Lesson on Quadratic Equations
Range of quadratic equations.

Solved Problems on Quadratic Equations
|
Solving the quadratic equation using the above method:
or, – 6 = 16. Solution: – 6 = 16. – 6 – 16 = 0 By factorisation method, ( – 8)( + 2) = 0 Therefore, x = 8 and x = -2 – 16 = 0. And check if the solution is correct. Solution: – 16 = 0. x – 4 = 0 [By algebraic identities] (x-4) (x+4) = 0 x = 4 and x = -4 Check: Putting the values of x in the LHS of the given quadratic equation If x = 4 X – 16 = (4) – 16 = 16 – 16 = 0 If x = -4, X – 16 = (-4) – 16 = 16 – 16 = 0 : = –2y + 2. Solution: Given, = –2y + 2 Rewriting the given equation; y + 2 y – 2 = 0 Using quadratic formula,
Therefore, y = -1 + √3 or y = -1 – √3 |
Applications of Quadratic Equations
Many real-life word problems can be solved using quadratic equations. While solving word problems, some common quadratic equation applications include speed problems and Geometry area problems.
- Solving the problems related to finding the area of quadrilateral such as rectangle, parallelogram and so on
- Solving Word Problems involving Distance, speed, and time, etc.,
Example: Find the width of a rectangle of area 336 cm2 if its length is equal to the 4 more than twice its width. Solution: Let x cm be the width of the rectangle. Length = (2x + 4) cm We know that Area of rectangle = Length x Width x(2x + 4) = 336 2x 2 + 4x – 336 = 0 x 2 + 2x – 168 = 0 x 2 + 14x – 12x – 168 = 0 x(x + 14) – 12(x + 14) = 0 (x + 14)(x – 12) = 0 x = -14, x = 12 Measurement cannot be negative. Therefore, Width of the rectangle = x = 12 cm
Practice Questions
- Solve x 2 + 2 x + 1 = 0.
- Solve 5x 2 + 6x + 1 = 0
- Solve 2x 2 + 3 x + 2 = 0.
- Solve x 2 − 4x + 6.25 = 0
Frequently Asked Questions on Quadratics
What is a quadratic equation, what are the methods to solve a quadratic equation, is x 2 – 1 a quadratic equation, what is the solution of x 2 + 4 = 0, write the quadratic equation in the form of sum and product of roots..
| MATHS Related Links | |
Leave a Comment Cancel reply
Your Mobile number and Email id will not be published. Required fields are marked *
Request OTP on Voice Call
Post My Comment
Thanks a lot ,This was very useful for me
x=√9 Squaring both the sides, x^2 = 9 x^2 – 9 = 0 It is a quadratic equation.
Register with BYJU'S & Download Free PDFs
Register with byju's & watch live videos.

IMAGES
VIDEO
COMMENTS
the factored expression is ( x + 2) ( x − 5) . The complete solution of the equation would go as follows: x 2 − 3 x − 10 = 0 ( x + 2) ( x − 5) = 0 Factor. ↙ ↘ x + 2 = 0 x − 5 = 0 x = − 2 x = 5. Now it's your turn to solve a few equations on your own. Keep in mind that different equations call for different factorization methods.
A quadratic equation is a polynomial equation in a single variable where the highest exponent of the variable is 2. There are three main ways to solve quadratic equations: 1) to factor the quadratic equation if you can do so, 2) to use the quadratic formula, or 3) to complete the square. If you want to know how to master these three methods ...
How to identify the most appropriate method to solve a quadratic equation. Try Factoring first. If the quadratic factors easily, this method is very quick. Try the Square Root Property next. If the equation fits the form \(a x^{2}=k\) or \(a(x-h)^{2}=k\), it can easily be solved by using the Square Root Property.
In math, a quadratic equation is a second-order polynomial equation in a single variable. It is written in the form: ax^2 + bx + c = 0 where x is the variable, and a, b, and c are constants, a ≠ 0.
A quadratic equation is an algebraic equation of the second degree in x. The quadratic equation in its standard form is ax 2 + bx + c = 0, where a and b are the coefficients, x is the variable, and c is the constant term. The important condition for an equation to be a quadratic equation is the coefficient of x 2 is a non-zero term (a ≠ 0). For writing a quadratic equation in standard form ...
There are different methods you can use to solve quadratic equations, depending on your particular problem. Solve By Factoring. Example: 3x^2-2x-1=0. Complete The Square. Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.) Take the Square Root. Example: 2x^2=18. Quadratic Formula
The 25/4 and 7 is the result of completing the square method. To factor the equation, you need to first follow this equation: x^ 2 + 2ax + a^2. In x^2 +5x = 3/4, The a^2 is missing. To figure out the a, you need to take the 5 and divide it by 2 (because 2ax), which becomes 5/2. a=5/2. Then you need to square it, (because a^2) which becomes 5^2/2^2.
How to Solve Quadratic Equations using Factoring Method. This is the easiest method of solving a quadratic equation as long as the binomial or trinomial is easily factorable. Otherwise, we will need other methods such as completing the square or using the quadratic formula. The following diagram illustrates the main approach to solving a ...
The solutions to a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 0 are given by the formula: x = −b ± √b2 − 4ac 2a. To use the Quadratic Formula, we substitute the values of a, b, and c from the standard form into the expression on the right side of the formula. Then we simplify the expression. The result is the pair of ...
Definition 7.3.1. The solutions to a quadratic equation of the form ax2 + bx + c = 0, where a ≠ 0 are given by the Quadratic Formula: x = − b ± √b2 − 4ac 2a. To use the Quadratic Formula, we substitute the values of a, b, and c from the standard form into the expression on the right side of the formula.
The solution of a quadratic equation is the value of x when you set the equation equal to zero. Graphically, since a quadratic equation represents a parabola. The solution (for real numbers) is where the parabola cross the x-axis. i.e. When you solve the following general equation: 0 = ax² + bx + c.
Worked example. First we need to identify the values for a, b, and c (the coefficients). First step, make sure the equation is in the format from above, a x 2 + b x + c = 0 : is what makes it a quadratic). Then we plug a , b , and c into the formula: solving this looks like: Therefore x = 3 or x = − 7 .
This method can be used to solve all types of quadratic equations, although it can be complicated for some types of equations. The method involves seven steps. Example 04: Solve equation $ 2x^2 + 8x - 10= 0$ by completing the square. Step 1: Divide the equation by the number in front of the square term.
Solving Quadratic Equation by Formula Method. The roots of the quadratic equation a x 2 + b x + c = 0 are given by the quadratic formula. x = - b ± b 2 - 4 a c 2 a. For example, consider the quadratic equation 3 x 2 - 5 x + 2 = 0. From the given quadratic equation a = 3, b = - 5, c = 2.
Quadratic Equation in Standard Form: ax 2 + bx + c = 0. Quadratic Equations can be factored. Quadratic Formula: x = −b ± √ (b2 − 4ac) 2a. When the Discriminant ( b2−4ac) is: positive, there are 2 real solutions. zero, there is one real solution. negative, there are 2 complex solutions.
To solve the quadratic equation using completing the square method, follow the below given steps. Now, divide the whole equation by a, such that the coefficient of x 2 is 1. Let us understand with the help of an example. Example: Solve 4x 2 + x = 3 by completing the square method. Solution: Given, 4x 2 + x = 3.
Example 5: Solve the quadratic equation below using the Quadratic Formula. First, we need to rewrite the given quadratic equation in Standard Form, [latex]a{x^2} + bx + c = 0[/latex]. Eliminate the [latex]{x^2}[/latex] term on the right side. Eliminate the [latex]x[/latex] term on the right side. Eliminate the constant on the right side.
Example of the quadratic formula to solve an equation. Use the formula to solve theQuadratic Equation: y = x2 + 2x + 1 y = x 2 + 2 x + 1 . Just substitute a,b, and c into the general formula: a = 1 b = 2 c = 1 a = 1 b = 2 c = 1. Below is a picture representing the graph of y = x² + 2x + 1 and its solution.
The quadratic formula helps us solve any quadratic equation. First, we bring the equation to the form ax²+bx+c=0, where a, b, and c are coefficients. Then, we plug these coefficients in the formula: (-b±√ (b²-4ac))/ (2a) . See examples of using the formula to solve a variety of equations. Created by Sal Khan.
Example 1: Solve the quadratic equation below using the Square Root Method. I will isolate the only [latex]{x^2}[/latex] term on the left side by adding both sides by [latex] + 1[/latex]. Then solve the values of [latex]x[/latex] by taking the square roots of both sides of the equation. As I mentioned before, we need to attach the plus or minus ...
Step 1: Enter the equation you want to solve using the quadratic formula. The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions. Quadratic Formula: x = −b±√b2 −4ac 2a x = − b ± b 2 − 4 a c 2 a.
FOIL method; Difference of Squares; Perfect Squares; Perfect Cubes; Trinomials; Binomial Expansion; Join; Cancel; Algebraic Properties. Exponents. Zero Rule; Negative Rule; ... Solve quadratic equations using quadratic formula step-by-step quadratic-equation-solve-using-quadratic-formula-calculator. en. Related Symbolab blog posts.
Quadratics or Quadratic Equations. Quadratics can be defined as a polynomial equation of a second degree, which implies that it comprises a minimum of one term that is squared. It is also called quadratic equations. The general form of the quadratic equation is: ax² + bx + c = 0. where x is an unknown variable and a, b, c are numerical ...