solving numerical optimization problems

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

4.7: Optimization Problems

• Last updated
• Save as PDF
• Page ID 4467

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Set up and solve optimization problems in several applied fields.

One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.

Solving Optimization Problems over a Closed, Bounded Interval

The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in Example \(\PageIndex{1}\), we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.

Example \(\PageIndex{1}\): Maximizing the Area of a Garden

A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides (Figure \(\PageIndex{1}\)). Given \(100\,\text{ft}\) of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?

Let \(x\) denote the length of the side of the garden perpendicular to the rock wall and \(y\) denote the length of the side parallel to the rock wall. Then the area of the garden is

\(A=x⋅y.\)

We want to find the maximum possible area subject to the constraint that the total fencing is \(100\,\text{ft}\). From Figure \(\PageIndex{1}\), the total amount of fencing used will be \(2x+y.\) Therefore, the constraint equation is

\(2x+y=100.\)

Solving this equation for \(y\), we have \(y=100−2x.\) Thus, we can write the area as

\(A(x)=x⋅(100−2x)=100x−2x^2.\)

Before trying to maximize the area function \(A(x)=100x−2x^2,\) we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need \(x>0\) and \(y>0\). Since \(y=100−2x\), if \(y>0\), then \(x<50\). Therefore, we are trying to determine the maximum value of \(A(x)\) for \(x\) over the open interval \((0,50)\). We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function \(A(x)=100x−2x^2\) over the closed interval \([0,50]\). If the maximum value occurs at an interior point, then we have found the value \(x\) in the open interval \((0,50)\) that maximizes the area of the garden.

Therefore, we consider the following problem:

Maximize \(A(x)=100x−2x^2\) over the interval \([0,50].\)

As mentioned earlier, since \(A\) is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical points. At the endpoints, \(A(x)=0\). Since the area is positive for all \(x\) in the open interval \((0,50)\), the maximum must occur at a critical point. Differentiating the function \(A(x)\), we obtain

\(A′(x)=100−4x.\)

Therefore, the only critical point is \(x=25\) (Figure \(\PageIndex{2}\)). We conclude that the maximum area must occur when \(x=25\).

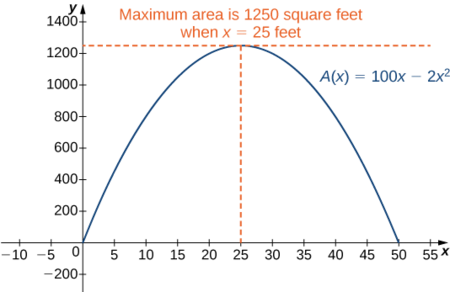
Then we have \(y=100−2x=100−2(25)=50.\) To maximize the area of the garden, let \(x=25\,\text{ft}\) and \(y=50\,\text{ft}\). The area of this garden is \(1250\, \text{ft}^2\).

Exercise \(\PageIndex{1}\)

Determine the maximum area if we want to make the same rectangular garden as in Figure \(\PageIndex{2}\), but we have \(200\,\text{ft}\) of fencing.

We need to maximize the function \(A(x)=200x−2x^2\) over the interval \([0,100].\)

The maximum area is \(5000\, \text{ft}^2\).

Now let’s look at a general strategy for solving optimization problems similar to Example \(\PageIndex{1}\).

Problem-Solving Strategy: Solving Optimization Problems

• Introduce all variables. If applicable, draw a figure and label all variables.
• Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
• Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable.
• Write any equations relating the independent variables in the formula from step \(3\). Use these equations to write the quantity to be maximized or minimized as a function of one variable.
• Identify the domain of consideration for the function in step \(4\) based on the physical problem to be solved.
• Locate the maximum or minimum value of the function from step \(4.\) This step typically involves looking for critical points and evaluating a function at endpoints.

Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.

Example \(\PageIndex{2}\): Maximizing the Volume of a Box

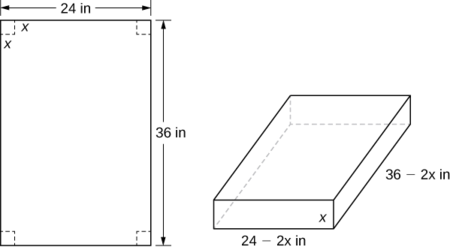
An open-top box is to be made from a \(24\,\text{in.}\) by \(36\,\text{in.}\) piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?

Step 1: Let \(x\) be the side length of the square to be removed from each corner (Figure \(\PageIndex{3}\)). Then, the remaining four flaps can be folded up to form an open-top box. Let \(V\) be the volume of the resulting box.

Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize \(V\).

Step 3: As mentioned in step 2, are trying to maximize the volume of a box. The volume of a box is

\[V=L⋅W⋅H \nonumber, \nonumber \]

where \(L,\,W,\)and \(H\) are the length, width, and height, respectively.

Step 4: From Figure \(\PageIndex{3}\), we see that the height of the box is \(x\) inches, the length is \(36−2x\) inches, and the width is \(24−2x\) inches. Therefore, the volume of the box is

\[ \begin{align*} V(x) &=(36−2x)(24−2x)x \\[4pt] &=4x^3−120x^2+864x \end{align*}. \nonumber \]

Step 5: To determine the domain of consideration, let’s examine Figure \(\PageIndex{3}\). Certainly, we need \(x>0.\) Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, \(24\,\text{in.}\); otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for \(x\) over the open interval \((0,12).\) Since \(V\) is a continuous function over the closed interval \([0,12]\), we know \(V\) will have an absolute maximum over the closed interval. Therefore, we consider \(V\) over the closed interval \([0,12]\) and check whether the absolute maximum occurs at an interior point.

Step 6: Since \(V(x)\) is a continuous function over the closed, bounded interval \([0,12]\), \(V\) must have an absolute maximum (and an absolute minimum). Since \(V(x)=0\) at the endpoints and \(V(x)>0\) for \(0<x<12,\) the maximum must occur at a critical point. The derivative is

\(V′(x)=12x^2−240x+864.\)

To find the critical points, we need to solve the equation

\(12x^2−240x+864=0.\)

Dividing both sides of this equation by \(12\), the problem simplifies to solving the equation

\(x^2−20x+72=0.\)

Using the quadratic formula, we find that the critical points are

\[\begin{align*} x &=\dfrac{20±\sqrt{(−20)^2−4(1)(72)}}{2} \\[4pt] &=\dfrac{20±\sqrt{112}}{2} \\[4pt] &=\dfrac{20±4\sqrt{7}}{2} \\[4pt] &=10±2\sqrt{7} \end{align*}. \nonumber \]

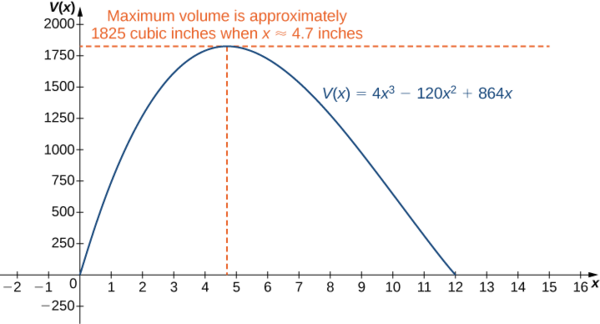
Since \(10+2\sqrt{7}\) is not in the domain of consideration, the only critical point we need to consider is \(10−2\sqrt{7}\). Therefore, the volume is maximized if we let \(x=10−2\sqrt{7}\,\text{in.}\) The maximum volume is

\[V(10−2\sqrt{7})=640+448\sqrt{7}≈1825\,\text{in}^3. \nonumber \]

as shown in the following graph.

Exercise \(\PageIndex{2}\)

Suppose the dimensions of the cardboard in Example \(\PageIndex{2}\) are \(20\,\text{in.}\) by \(30\,\text{in.}\) Let \(x\) be the side length of each square and write the volume of the open-top box as a function of \(x\). Determine the domain of consideration for \(x\).

The volume of the box is \(L⋅W⋅H.\)

\(V(x)=x(20−2x)(30−2x).\) The domain is \([0,10]\).

Example \(\PageIndex{3}\): Minimizing Travel Time

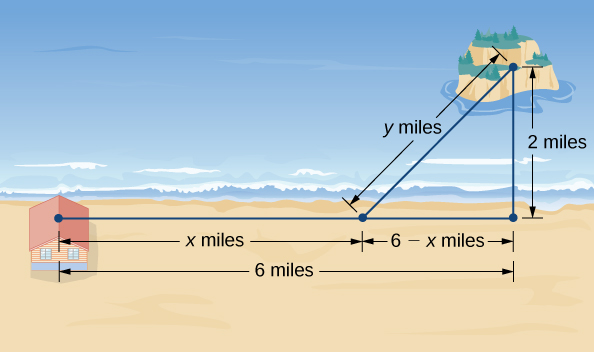
An island is \(2\) mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is \(6\) mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of \(8\) mph and swims at a rate of \(3\) mph. How far should the visitor run before swimming to minimize the time it takes to reach the island?

Step 1: Let \(x\) be the distance running and let \(y\) be the distance swimming (Figure \(\PageIndex{5}\)). Let \(T\) be the time it takes to get from the cabin to the island.

Step 2: The problem is to minimize \(T\).

Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = Rate × Time \((D=R×T),\) the time spent running is

\(T_{running}=\dfrac{D_{running}}{R_{running}}=\dfrac{x}{8}\),

and the time spent swimming is

\(T_{swimming}=\dfrac{D_{swimming}}{R_{swimming}}=\dfrac{y}{3}\).

Therefore, the total time spent traveling is

\(T=\dfrac{x}{8}+\dfrac{y}{3}\).

Step 4: From Figure \(\PageIndex{5}\), the line segment of \(y\) miles forms the hypotenuse of a right triangle with legs of length \(2\) mi and \(6−x\) mi. Therefore, by the Pythagorean theorem, \(2^2+(6−x)^2=y^2\), and we obtain \(y=\sqrt{(6−x)^2+4}\). Thus, the total time spent traveling is given by the function

\(T(x)=\dfrac{x}{8}+\dfrac{\sqrt{(6−x)^2+4}}{3}\).

Step 5: From Figure \(\PageIndex{5}\), we see that \(0≤x≤6\). Therefore, \([0,6]\) is the domain of consideration.

Step 6: Since \(T(x)\) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of \(T\) over the interval \([0,6].\) The derivative is

\[\begin{align*} T′(x) &=\dfrac{1}{8}−\dfrac{1}{2}\dfrac{[(6−x)^2+4]^{−1/2}}{3}⋅2(6−x) \\[4pt] &=\dfrac{1}{8}−\dfrac{(6−x)}{3\sqrt{(6−x)^2+4}} \end{align*}\]

If \(T′(x)=0,\), then

\[\dfrac{1}{8}=\dfrac{6−x}{3\sqrt{(6−x)^2+4}} \label{ex3eq1} \]

\[3\sqrt{(6−x)^2+4}=8(6−x). \label{ex3eq2} \]

Squaring both sides of this equation, we see that if \(x\) satisfies this equation, then \(x\) must satisfy

\[9[(6−x)^2+4]=64(6−x)^2,\nonumber \]

which implies

\[55(6−x)^2=36. \nonumber \]

We conclude that if \(x\) is a critical point, then \(x\) satisfies

\[(x−6)^2=\dfrac{36}{55}. \nonumber \]

[Note that since we are squaring, \( (x-6)^2 = (6-x)^2.\)]

Therefore, the possibilities for critical points are

\[x=6±\dfrac{6}{\sqrt{55}}.\nonumber \]

Since \(x=6+6/\sqrt{55}\) is not in the domain, it is not a possibility for a critical point. On the other hand, \(x=6−6/\sqrt{55}\) is in the domain. Since we squared both sides of Equation \ref{ex3eq2} to arrive at the possible critical points, it remains to verify that \(x=6−6/\sqrt{55}\) satisfies Equation \ref{ex3eq1}. Since \(x=6−6/\sqrt{55}\) does satisfy that equation, we conclude that \(x=6−6/\sqrt{55}\) is a critical point, and it is the only one. To justify that the time is minimized for this value of \(x\), we just need to check the values of \(T(x)\) at the endpoints \(x=0\) and \(x=6\), and compare them with the value of \(T(x)\) at the critical point \(x=6−6/\sqrt{55}\). We find that \(T(0)≈2.108\,\text{h}\) and \(T(6)≈1.417\,\text{h}\), whereas

\[T(6−6/\sqrt{55})≈1.368\,\text{h}. \nonumber \]

Therefore, we conclude that \(T\) has a local minimum at \(x≈5.19\) mi.

Exercise \(\PageIndex{3}\)

Suppose the island is \(1\) mi from shore, and the distance from the cabin to the point on the shore closest to the island is \(15\) mi. Suppose a visitor swims at the rate of \(2.5\) mph and runs at a rate of \(6\) mph. Let \(x\) denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.

The time \(T=T_{running}+T_{swimming}.\)

\(T(x)=\dfrac{x}{6}+\dfrac{\sqrt{(15−x)^2+1}}{2.5} \)

In business, companies are interested in maximizing revenue. In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.

Example \(\PageIndex{4}\): Maximizing Revenue

Owners of a car rental company have determined that if they charge customers \(p\) dollars per day to rent a car, where \(50≤p≤200\), the number of cars \(n\) they rent per day can be modeled by the linear function \(n(p)=1000−5p\). If they charge \($50\) per day or less, they will rent all their cars. If they charge \($200\) per day or more, they will not rent any cars. Assuming the owners plan to charge customers between \($50\) per day and \($200\) per day to rent a car, how much should they charge to maximize their revenue?

Step 1: Let \(p\) be the price charged per car per day and let \(n\) be the number of cars rented per day. Let \(R\) be the revenue per day.

Step 2: The problem is to maximize \(R.\)

Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, \(R=n×p.\)

Step 4: Since the number of cars rented per day is modeled by the linear function \(n(p)=1000−5p,\) the revenue \(R\) can be represented by the function

\[ \begin{align*} R(p) &=n×p \\[4pt] &=(1000−5p)p \\[4pt] &=−5p^2+1000p.\end{align*}\]

Step 5: Since the owners plan to charge between \($50\) per car per day and \($200\) per car per day, the problem is to find the maximum revenue \(R(p)\) for \(p\) in the closed interval \([50,200]\).

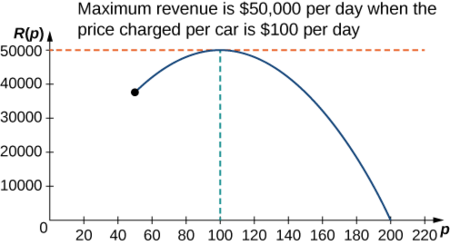
Step 6: Since \(R\) is a continuous function over the closed, bounded interval \([50,200]\), it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is \(R′(p)=−10p+1000.\) Therefore, the critical point is \(p=100\). When \(p=100, R(100)=$50,000.\) When \(p=50, R(p)=$37,500\). When \(p=200, R(p)=$0\).

Therefore, the absolute maximum occurs at \(p=$100\). The car rental company should charge \($100\) per day per car to maximize revenue as shown in the following figure.

Exercise \(\PageIndex{4}\)

A car rental company charges its customers \(p\) dollars per day, where \(60≤p≤150\). It has found that the number of cars rented per day can be modeled by the linear function \(n(p)=750−5p.\) How much should the company charge each customer to maximize revenue?

\(R(p)=n×p,\) where \(n\) is the number of cars rented and \(p\) is the price charged per car.

The company should charge \($75\) per car per day.

Example \(\PageIndex{5}\): Maximizing the Area of an Inscribed Rectangle

A rectangle is to be inscribed in the ellipse

\[\dfrac{x^2}{4}+y^2=1. \nonumber \]

What should the dimensions of the rectangle be to maximize its area? What is the maximum area?

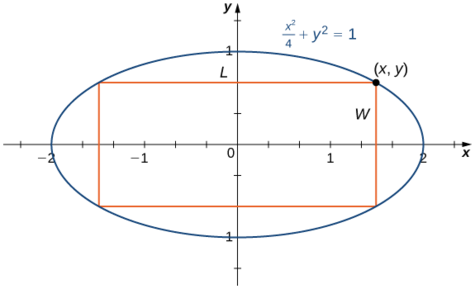
Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let \(L\) be the length of the rectangle and \(W\) be its width. Let \(A\) be the area of the rectangle.

Step 2: The problem is to maximize \(A\).

Step 3: The area of the rectangle is \(A=LW.\)

Step 4: Let \((x,y)\) be the corner of the rectangle that lies in the first quadrant, as shown in Figure \(\PageIndex{7}\). We can write length \(L=2x\) and width \(W=2y\). Since \(\dfrac{x^2}{4}+y^2=1\) and \(y>0\), we have \(y=\sqrt{1-\dfrac{x^2}{4}}\). Therefore, the area is

\(A=LW=(2x)(2y)=4x\sqrt{1-\dfrac{x^2}{4}}=2x\sqrt{4−x^2}\)

Step 5: From Figure \(\PageIndex{7}\), we see that to inscribe a rectangle in the ellipse, the \(x\)-coordinate of the corner in the first quadrant must satisfy \(0<x<2\). Therefore, the problem reduces to looking for the maximum value of \(A(x)\) over the open interval \((0,2)\). Since \(A(x)\) will have an absolute maximum (and absolute minimum) over the closed interval \([0,2]\), we consider \(A(x)=2x\sqrt{4−x^2}\) over the interval \([0,2]\). If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.

Step 6: As mentioned earlier, \(A(x)\) is a continuous function over the closed, bounded interval \([0,2]\). Therefore, it has an absolute maximum (and absolute minimum). At the endpoints \(x=0\) and \(x=2\), \(A(x)=0.\) For \(0<x<2\), \(A(x)>0\).

Therefore, the maximum must occur at a critical point. Taking the derivative of \(A(x)\), we obtain

\[ \begin{align*} A'(x) &=2\sqrt{4−x^2}+2x⋅\dfrac{1}{2\sqrt{4−x^2}}(−2x) \\[4pt] &=2\sqrt{4−x^2}−\dfrac{2x^2}{\sqrt{4−x^2}} \\[4pt] &=\dfrac{8−4x^2}{\sqrt{4−x^2}} . \end{align*}\]

To find critical points, we need to find where \(A'(x)=0.\) We can see that if \(x\) is a solution of

\[\dfrac{8−4x^2}{\sqrt{4−x^2}}=0, \label{ex5eq1} \]

then \(x\) must satisfy

\[8−4x^2=0. \nonumber \]

Therefore, \(x^2=2.\) Thus, \(x=±\sqrt{2}\) are the possible solutions of Equation \ref{ex5eq1}. Since we are considering \(x\) over the interval \([0,2]\), \(x=\sqrt{2}\) is a possibility for a critical point, but \(x=−\sqrt{2}\) is not. Therefore, we check whether \(\sqrt{2}\) is a solution of Equation \ref{ex5eq1}. Since \(x=\sqrt{2}\) is a solution of Equation \ref{ex5eq1}, we conclude that \(\sqrt{2}\) is the only critical point of \(A(x)\) in the interval \([0,2]\).

Therefore, \(A(x)\) must have an absolute maximum at the critical point \(x=\sqrt{2}\). To determine the dimensions of the rectangle, we need to find the length \(L\) and the width \(W\). If \(x=\sqrt{2}\) then

\[y=\sqrt{1−\dfrac{(\sqrt{2})^2}{4}}=\sqrt{1−\dfrac{1}{2}}=\dfrac{1}{\sqrt{2}}.\nonumber \]

Therefore, the dimensions of the rectangle are \(L=2x=2\sqrt{2}\) and \(W=2y=\dfrac{2}{\sqrt{2}}=\sqrt{2}\). The area of this rectangle is \( A=LW=(2\sqrt{2})(\sqrt{2})=4.\)

Exercise \(\PageIndex{5}\)

Modify the area function \(A\) if the rectangle is to be inscribed in the unit circle \(x^2+y^2=1\). What is the domain of consideration?

If \((x,y)\) is the vertex of the square that lies in the first quadrant, then the area of the square is \(A=(2x)(2y)=4xy.\)

\(A(x)=4x\sqrt{1−x^2}.\) The domain of consideration is \([0,1]\).

Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded

In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.

Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function \(f(x)=x^2+4\) over \((−∞,∞)\) has an absolute minimum of \(4\) at \(x=0\). Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is \((0,∞),\) the function has an absolute minimum.

In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.

Example \(\PageIndex{6}\): Minimizing Surface Area

A rectangular box with a square base, an open top, and a volume of \(216 \,\text{in}^3\) is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?

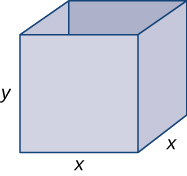
Step 1: Draw a rectangular box and introduce the variable \(x\) to represent the length of each side of the square base; let \(y\) represent the height of the box. Let \(S\) denote the surface area of the open-top box.

Step 2: We need to minimize the surface area. Therefore, we need to minimize \(S\).

Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is \(x⋅y.\) The area of the base is \(x^2\). Therefore, the surface area of the box is

\(S=4xy+x^2\).

Step 4: Since the volume of this box is \(x^2y\) and the volume is given as \(216\,\text{in}^3\), the constraint equation is

\(x^2y=216\).

Solving the constraint equation for \(y\), we have \(y=\dfrac{216}{x^2}\). Therefore, we can write the surface area as a function of \(x\) only:

\[S(x)=4x\left(\dfrac{216}{x^2}\right)+x^2.\nonumber \]

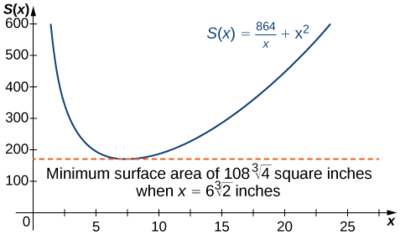
Therefore, \(S(x)=\dfrac{864}{x}+x^2\).

Step 5: Since we are requiring that \(x^2y=216\), we cannot have \(x=0\). Therefore, we need \(x>0\). On the other hand, \(x\) is allowed to have any positive value. Note that as \(x\) becomes large, the height of the box \(y\) becomes correspondingly small so that \(x^2y=216\). Similarly, as \(x\) becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval \((0,∞)\). Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval \((0,∞).\)

Step 6: Note that as \(x→0^+,\, S(x)→∞.\) Also, as \(x→∞, \,S(x)→∞\). Since \(S\) is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some \(x∈(0,∞)\). This minimum must occur at a critical point of \(S\). The derivative is

\[S′(x)=−\dfrac{864}{x^2}+2x.\nonumber \]

Therefore, \(S′(x)=0\) when \(2x=\dfrac{864}{x^2}\). Solving this equation for \(x\), we obtain \(x^3=432\), so \(x=\sqrt[3]{432}=6\sqrt[3]{2}.\) Since this is the only critical point of \(S\), the absolute minimum must occur at \(x=6\sqrt[3]{2}\) (see Figure \(\PageIndex{9}\)).

When \(x=6\sqrt[3]{2}\), \(y=\dfrac{216}{(6\sqrt[3]{2})^2}=3\sqrt[3]{2}\,\text{in.}\) Therefore, the dimensions of the box should be \(x=6\sqrt[3]{2}\,\text{in.}\) and \(y=3\sqrt[3]{2}\,\text{in.}\) With these dimensions, the surface area is

\[S(6\sqrt[3]{2})=\dfrac{864}{6\sqrt[3]{2}}+(6\sqrt[3]{2})^2=108\sqrt[3]{4}\,\text{in}^2\nonumber \]

Exercise \(\PageIndex{6}\)

Consider the same open-top box, which is to have volume \(216\,\text{in}^3\). Suppose the cost of the material for the base is \(20¢/\text{in}^2\) and the cost of the material for the sides is \(30¢/\text{in}^2\) and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let \(x\) be the side length of the base and \(y\) be the height of the box.)

If the cost of one of the sides is \(30¢/\text{in}^2,\) the cost of that side is \(0.30xy\) dollars.

\(c(x)=\dfrac{259.2}{x}+0.2x^2\) dollars

Key Concepts

• To solve an optimization problem, begin by drawing a picture and introducing variables.
• Find an equation relating the variables.
• Find a function of one variable to describe the quantity that is to be minimized or maximized.
• Look for critical points to locate local extrema.

4.7 Applied Optimization Problems

Learning objectives.

• 4.7.1 Set up and solve optimization problems in several applied fields.

One common application of calculus is calculating the minimum or maximum value of a function. For example, companies often want to minimize production costs or maximize revenue. In manufacturing, it is often desirable to minimize the amount of material used to package a product with a certain volume. In this section, we show how to set up these types of minimization and maximization problems and solve them by using the tools developed in this chapter.

Solving Optimization Problems over a Closed, Bounded Interval

The basic idea of the optimization problems that follow is the same. We have a particular quantity that we are interested in maximizing or minimizing. However, we also have some auxiliary condition that needs to be satisfied. For example, in Example 4.32 , we are interested in maximizing the area of a rectangular garden. Certainly, if we keep making the side lengths of the garden larger, the area will continue to become larger. However, what if we have some restriction on how much fencing we can use for the perimeter? In this case, we cannot make the garden as large as we like. Let’s look at how we can maximize the area of a rectangle subject to some constraint on the perimeter.

Example 4.32

Maximizing the area of a garden.

A rectangular garden is to be constructed using a rock wall as one side of the garden and wire fencing for the other three sides ( Figure 4.62 ). Given 100 100 ft of wire fencing, determine the dimensions that would create a garden of maximum area. What is the maximum area?

Let x x denote the length of the side of the garden perpendicular to the rock wall and y y denote the length of the side parallel to the rock wall. Then the area of the garden is

We want to find the maximum possible area subject to the constraint that the total fencing is 100 ft . 100 ft . From Figure 4.62 , the total amount of fencing used will be 2 x + y . 2 x + y . Therefore, the constraint equation is

Solving this equation for y , y , we have y = 100 − 2 x . y = 100 − 2 x . Thus, we can write the area as

Before trying to maximize the area function A ( x ) = 100 x − 2 x 2 , A ( x ) = 100 x − 2 x 2 , we need to determine the domain under consideration. To construct a rectangular garden, we certainly need the lengths of both sides to be positive. Therefore, we need x > 0 x > 0 and y > 0 . y > 0 . Since y = 100 − 2 x , y = 100 − 2 x , if y > 0 , y > 0 , then x < 50 . x < 50 . Therefore, we are trying to determine the maximum value of A ( x ) A ( x ) for x x over the open interval ( 0 , 50 ) . ( 0 , 50 ) . We do not know that a function necessarily has a maximum value over an open interval. However, we do know that a continuous function has an absolute maximum (and absolute minimum) over a closed interval. Therefore, let’s consider the function A ( x ) = 100 x − 2 x 2 A ( x ) = 100 x − 2 x 2 over the closed interval [ 0 , 50 ] . [ 0 , 50 ] . If the maximum value occurs at an interior point, then we have found the value x x in the open interval ( 0 , 50 ) ( 0 , 50 ) that maximizes the area of the garden. Therefore, we consider the following problem:

Maximize A ( x ) = 100 x − 2 x 2 A ( x ) = 100 x − 2 x 2 over the interval [ 0 , 50 ] . [ 0 , 50 ] .

As mentioned earlier, since A A is a continuous function on a closed, bounded interval, by the extreme value theorem, it has a maximum and a minimum. These extreme values occur either at endpoints or critical points. At the endpoints, A ( x ) = 0 . A ( x ) = 0 . Since the area is positive for all x x in the open interval ( 0 , 50 ) , ( 0 , 50 ) , the maximum must occur at a critical point. Differentiating the function A ( x ) , A ( x ) , we obtain

Therefore, the only critical point is x = 25 x = 25 ( Figure 4.63 ). We conclude that the maximum area must occur when x = 25 . x = 25 . Then we have y = 100 − 2 x = 100 − 2 ( 25 ) = 50 . y = 100 − 2 x = 100 − 2 ( 25 ) = 50 . To maximize the area of the garden, let x = 25 x = 25 ft and y = 50 ft . y = 50 ft . The area of this garden is 1250 ft 2 . 1250 ft 2 .

Checkpoint 4.31

Determine the maximum area if we want to make the same rectangular garden as in Figure 4.63 , but we have 200 200 ft of fencing.

Now let’s look at a general strategy for solving optimization problems similar to Example 4.32 .

Problem-Solving Strategy

Problem-solving strategy: solving optimization problems.

• Introduce all variables. If applicable, draw a figure and label all variables.
• Determine which quantity is to be maximized or minimized, and for what range of values of the other variables (if this can be determined at this time).
• Write a formula for the quantity to be maximized or minimized in terms of the variables. This formula may involve more than one variable.
• Write any equations relating the independent variables in the formula from step 3 . 3 . Use these equations to write the quantity to be maximized or minimized as a function of one variable.
• Identify the domain of consideration for the function in step 4 4 based on the physical problem to be solved.
• Locate the maximum or minimum value of the function from step 4 . 4 . This step typically involves looking for critical points and evaluating a function at endpoints.

Now let’s apply this strategy to maximize the volume of an open-top box given a constraint on the amount of material to be used.

Example 4.33

Maximizing the volume of a box.

An open-top box is to be made from a 24 24 in. by 36 36 in. piece of cardboard by removing a square from each corner of the box and folding up the flaps on each side. What size square should be cut out of each corner to get a box with the maximum volume?

Step 1: Let x x be the side length of the square to be removed from each corner ( Figure 4.64 ). Then, the remaining four flaps can be folded up to form an open-top box. Let V V be the volume of the resulting box.

Step 2: We are trying to maximize the volume of a box. Therefore, the problem is to maximize V . V .

Step 3: As mentioned in step 2 , 2 , we are trying to maximize the volume of a box. The volume of a box is V = L · W · H , V = L · W · H , where L , W , and H L , W , and H are the length, width, and height, respectively.

Step 4: From Figure 4.64 , we see that the height of the box is x x inches, the length is 36 − 2 x 36 − 2 x inches, and the width is 24 − 2 x 24 − 2 x inches. Therefore, the volume of the box is

Step 5: To determine the domain of consideration, let’s examine Figure 4.64 . Certainly, we need x > 0 . x > 0 . Furthermore, the side length of the square cannot be greater than or equal to half the length of the shorter side, 24 24 in.; otherwise, one of the flaps would be completely cut off. Therefore, we are trying to determine whether there is a maximum volume of the box for x x over the open interval ( 0 , 12 ) . ( 0 , 12 ) . Since V V is a continuous function over the closed interval [ 0 , 12 ] , [ 0 , 12 ] , we know V V will have an absolute maximum over the closed interval. Therefore, we consider V V over the closed interval [ 0 , 12 ] [ 0 , 12 ] and check whether the absolute maximum occurs at an interior point.

Step 6: Since V ( x ) V ( x ) is a continuous function over the closed, bounded interval [ 0 , 12 ] , [ 0 , 12 ] , V V must have an absolute maximum (and an absolute minimum). Since V ( x ) = 0 V ( x ) = 0 at the endpoints and V ( x ) > 0 V ( x ) > 0 for 0 < x < 12 , 0 < x < 12 , the maximum must occur at a critical point. The derivative is

To find the critical points, we need to solve the equation

Dividing both sides of this equation by 12 , 12 , the problem simplifies to solving the equation

Using the quadratic formula, we find that the critical points are

Since 10 + 2 7 10 + 2 7 is not in the domain of consideration, the only critical point we need to consider is 10 − 2 7 . 10 − 2 7 . Therefore, the volume is maximized if we let x = 10 − 2 7 in . x = 10 − 2 7 in . The maximum volume is V ( 10 − 2 7 ) = 640 + 448 7 ≈ 1825 in . 3 V ( 10 − 2 7 ) = 640 + 448 7 ≈ 1825 in . 3 as shown in the following graph.

Watch a video about optimizing the volume of a box.

Checkpoint 4.32

Suppose the dimensions of the cardboard in Example 4.33 are 20 in. by 30 in. Let x x be the side length of each square and write the volume of the open-top box as a function of x . x . Determine the domain of consideration for x . x .

Example 4.34

Minimizing travel time.

An island is 2 mi 2 mi due north of its closest point along a straight shoreline. A visitor is staying at a cabin on the shore that is 6 mi 6 mi west of that point. The visitor is planning to go from the cabin to the island. Suppose the visitor runs at a rate of 8 mph 8 mph and swims at a rate of 3 mph . 3 mph . How far should the visitor run before swimming to minimize the time it takes to reach the island?

Step 1: Let x x be the distance running and let y y be the distance swimming ( Figure 4.66 ). Let T T be the time it takes to get from the cabin to the island.

Step 2: The problem is to minimize T . T .

Step 3: To find the time spent traveling from the cabin to the island, add the time spent running and the time spent swimming. Since Distance = = Rate × × Time ( D = R × T ) , ( D = R × T ) , the time spent running is

and the time spent swimming is

Therefore, the total time spent traveling is

Step 4: From Figure 4.66 , the line segment of y y miles forms the hypotenuse of a right triangle with legs of length 2 mi 2 mi and 6 − x mi . 6 − x mi . Therefore, by the Pythagorean theorem, 2 2 + ( 6 − x ) 2 = y 2 , 2 2 + ( 6 − x ) 2 = y 2 , and we obtain y = ( 6 − x ) 2 + 4 . y = ( 6 − x ) 2 + 4 . Thus, the total time spent traveling is given by the function

Step 5: From Figure 4.66 , we see that 0 ≤ x ≤ 6 . 0 ≤ x ≤ 6 . Therefore, [ 0 , 6 ] [ 0 , 6 ] is the domain of consideration.

Step 6: Since T ( x ) T ( x ) is a continuous function over a closed, bounded interval, it has a maximum and a minimum. Let’s begin by looking for any critical points of T T over the interval [ 0 , 6 ] . [ 0 , 6 ] . The derivative is

If T ′ ( x ) = 0 , T ′ ( x ) = 0 , then

Squaring both sides of this equation, we see that if x x satisfies this equation, then x x must satisfy

which implies

We conclude that if x x is a critical point, then x x satisfies

Therefore, the possibilities for critical points are

Since x = 6 + 6 / 55 x = 6 + 6 / 55 is not in the domain, it is not a possibility for a critical point. On the other hand, x = 6 − 6 / 55 x = 6 − 6 / 55 is in the domain. Since we squared both sides of Equation 4.6 to arrive at the possible critical points, it remains to verify that x = 6 − 6 / 55 x = 6 − 6 / 55 satisfies Equation 4.6 . Since x = 6 − 6 / 55 x = 6 − 6 / 55 does satisfy that equation, we conclude that x = 6 − 6 / 55 x = 6 − 6 / 55 is a critical point, and it is the only one. To justify that the time is minimized for this value of x , x , we just need to check the values of T ( x ) T ( x ) at the endpoints x = 0 x = 0 and x = 6 , x = 6 , and compare them with the value of T ( x ) T ( x ) at the critical point x = 6 − 6 / 55 . x = 6 − 6 / 55 . We find that T ( 0 ) ≈ 2.108 h T ( 0 ) ≈ 2.108 h and T ( 6 ) ≈ 1.417 h, T ( 6 ) ≈ 1.417 h, whereas T ( 6 − 6 / 55 ) ≈ 1.368 h . T ( 6 − 6 / 55 ) ≈ 1.368 h . Therefore, we conclude that T T has a local minimum at x ≈ 5.19 x ≈ 5.19 mi.

Checkpoint 4.33

Suppose the island is 1 1 mi from shore, and the distance from the cabin to the point on the shore closest to the island is 15 mi . 15 mi . Suppose a visitor swims at the rate of 2.5 mph 2.5 mph and runs at a rate of 6 mph . 6 mph . Let x x denote the distance the visitor will run before swimming, and find a function for the time it takes the visitor to get from the cabin to the island.

In business, companies are interested in maximizing revenue . In the following example, we consider a scenario in which a company has collected data on how many cars it is able to lease, depending on the price it charges its customers to rent a car. Let’s use these data to determine the price the company should charge to maximize the amount of money it brings in.

Example 4.35

Maximizing revenue.

Owners of a car rental company have determined that if they charge customers p p dollars per day to rent a car, where 50 ≤ p ≤ 200 , 50 ≤ p ≤ 200 , the number of cars n n they rent per day can be modeled by the linear function n ( p ) = 1000 − 5 p . n ( p ) = 1000 − 5 p . If they charge $ 50 $ 50 per day or less, they will rent all their cars. If they charge $ 200 $ 200 per day or more, they will not rent any cars. Assuming the owners plan to charge customers between $50 per day and $ 200 $ 200 per day to rent a car, how much should they charge to maximize their revenue?

Step 1: Let p p be the price charged per car per day and let n n be the number of cars rented per day. Let R R be the revenue per day.

Step 2: The problem is to maximize R . R .

Step 3: The revenue (per day) is equal to the number of cars rented per day times the price charged per car per day—that is, R = n × p . R = n × p .

Step 4: Since the number of cars rented per day is modeled by the linear function n ( p ) = 1000 − 5 p , n ( p ) = 1000 − 5 p , the revenue R R can be represented by the function

Step 5: Since the owners plan to charge between $ 50 $ 50 per car per day and $ 200 $ 200 per car per day, the problem is to find the maximum revenue R ( p ) R ( p ) for p p in the closed interval [ 50 , 200 ] . [ 50 , 200 ] .

Step 6: Since R R is a continuous function over the closed, bounded interval [ 50 , 200 ] , [ 50 , 200 ] , it has an absolute maximum (and an absolute minimum) in that interval. To find the maximum value, look for critical points. The derivative is R ′ ( p ) = −10 p + 1000 . R ′ ( p ) = −10 p + 1000 . Therefore, the critical point is p = 100 p = 100 When p = 100 , p = 100 , R ( 100 ) = $ 50,000 . R ( 100 ) = $ 50,000 . When p = 50 , p = 50 , R ( p ) = $ 37,500 . R ( p ) = $ 37,500 . When p = 200 , p = 200 , R ( p ) = $ 0 . R ( p ) = $ 0 . Therefore, the absolute maximum occurs at p = $ 100 . p = $ 100 . The car rental company should charge $ 100 $ 100 per day per car to maximize revenue as shown in the following figure.

Checkpoint 4.34

A car rental company charges its customers p p dollars per day, where 60 ≤ p ≤ 150 . 60 ≤ p ≤ 150 . It has found that the number of cars rented per day can be modeled by the linear function n ( p ) = 750 − 5 p . n ( p ) = 750 − 5 p . How much should the company charge each customer to maximize revenue?

Example 4.36

Maximizing the area of an inscribed rectangle.

A rectangle is to be inscribed in the ellipse

What should the dimensions of the rectangle be to maximize its area? What is the maximum area?

Step 1: For a rectangle to be inscribed in the ellipse, the sides of the rectangle must be parallel to the axes. Let L L be the length of the rectangle and W W be its width. Let A A be the area of the rectangle.

Step 2: The problem is to maximize A . A .

Step 3: The area of the rectangle is A = L W . A = L W .

Step 4: Let ( x , y ) ( x , y ) be the corner of the rectangle that lies in the first quadrant, as shown in Figure 4.68 . We can write length L = 2 x L = 2 x and width W = 2 y . W = 2 y . Since x 2 4 + y 2 = 1 x 2 4 + y 2 = 1 and y > 0 , y > 0 , we have y = 1 − x 2 4 . y = 1 − x 2 4 . Therefore, the area is

Step 5: From Figure 4.68 , we see that to inscribe a rectangle in the ellipse, the x x -coordinate of the corner in the first quadrant must satisfy 0 < x < 2 . 0 < x < 2 . Therefore, the problem reduces to looking for the maximum value of A ( x ) A ( x ) over the open interval ( 0 , 2 ) . ( 0 , 2 ) . Since A ( x ) A ( x ) will have an absolute maximum (and absolute minimum) over the closed interval [ 0 , 2 ] , [ 0 , 2 ] , we consider A ( x ) = 2 x 4 − x 2 A ( x ) = 2 x 4 − x 2 over the interval [ 0 , 2 ] . [ 0 , 2 ] . If the absolute maximum occurs at an interior point, then we have found an absolute maximum in the open interval.

Step 6: As mentioned earlier, A ( x ) A ( x ) is a continuous function over the closed, bounded interval [ 0 , 2 ] . [ 0 , 2 ] . Therefore, it has an absolute maximum (and absolute minimum). At the endpoints x = 0 x = 0 and x = 2 , x = 2 , A ( x ) = 0 . A ( x ) = 0 . For 0 < x < 2 , 0 < x < 2 , A ( x ) > 0 . A ( x ) > 0 . Therefore, the maximum must occur at a critical point. Taking the derivative of A ( x ) , A ( x ) , we obtain

To find critical points, we need to find where A ′ ( x ) = 0 . A ′ ( x ) = 0 . We can see that if x x is a solution of

then x x must satisfy

Therefore, x 2 = 2 . x 2 = 2 . Thus, x = ± 2 x = ± 2 are the possible solutions of Equation 4.7 . Since we are considering x x over the interval [ 0 , 2 ] , [ 0 , 2 ] , x = 2 x = 2 is a possibility for a critical point, but x = − 2 x = − 2 is not. Therefore, we check whether 2 2 is a solution of Equation 4.7 . Since x = 2 x = 2 is a solution of Equation 4.7 , we conclude that 2 2 is the only critical point of A ( x ) A ( x ) in the interval [ 0 , 2 ] . [ 0 , 2 ] . Therefore, A ( x ) A ( x ) must have an absolute maximum at the critical point x = 2 . x = 2 . To determine the dimensions of the rectangle, we need to find the length L L and the width W . W . If x = 2 x = 2 then

Therefore, the dimensions of the rectangle are L = 2 x = 2 2 L = 2 x = 2 2 and W = 2 y = 2 2 = 2 . W = 2 y = 2 2 = 2 . The area of this rectangle is A = L W = ( 2 2 ) ( 2 ) = 4 . A = L W = ( 2 2 ) ( 2 ) = 4 .

Checkpoint 4.35

Modify the area function A A if the rectangle is to be inscribed in the unit circle x 2 + y 2 = 1 . x 2 + y 2 = 1 . What is the domain of consideration?

Solving Optimization Problems when the Interval Is Not Closed or Is Unbounded

In the previous examples, we considered functions on closed, bounded domains. Consequently, by the extreme value theorem, we were guaranteed that the functions had absolute extrema. Let’s now consider functions for which the domain is neither closed nor bounded.

Many functions still have at least one absolute extrema, even if the domain is not closed or the domain is unbounded. For example, the function f ( x ) = x 2 + 4 f ( x ) = x 2 + 4 over ( − ∞ , ∞ ) ( − ∞ , ∞ ) has an absolute minimum of 4 4 at x = 0 . x = 0 . Therefore, we can still consider functions over unbounded domains or open intervals and determine whether they have any absolute extrema. In the next example, we try to minimize a function over an unbounded domain. We will see that, although the domain of consideration is ( 0 , ∞ ) , ( 0 , ∞ ) , the function has an absolute minimum.

In the following example, we look at constructing a box of least surface area with a prescribed volume. It is not difficult to show that for a closed-top box, by symmetry, among all boxes with a specified volume, a cube will have the smallest surface area. Consequently, we consider the modified problem of determining which open-topped box with a specified volume has the smallest surface area.

Example 4.37

Minimizing surface area.

A rectangular box with a square base, an open top, and a volume of 216 216 in. 3 is to be constructed. What should the dimensions of the box be to minimize the surface area of the box? What is the minimum surface area?

Step 1: Draw a rectangular box and introduce the variable x x to represent the length of each side of the square base; let y y represent the height of the box. Let S S denote the surface area of the open-top box.

Step 2: We need to minimize the surface area. Therefore, we need to minimize S . S .

Step 3: Since the box has an open top, we need only determine the area of the four vertical sides and the base. The area of each of the four vertical sides is x · y . x · y . The area of the base is x 2 . x 2 . Therefore, the surface area of the box is

Step 4: Since the volume of this box is x 2 y x 2 y and the volume is given as 216 in . 3 , 216 in . 3 , the constraint equation is

Solving the constraint equation for y , y , we have y = 216 x 2 . y = 216 x 2 . Therefore, we can write the surface area as a function of x x only:

Therefore, S ( x ) = 864 x + x 2 . S ( x ) = 864 x + x 2 .

Step 5: Since we are requiring that x 2 y = 216 , x 2 y = 216 , we cannot have x = 0 . x = 0 . Therefore, we need x > 0 . x > 0 . On the other hand, x x is allowed to have any positive value. Note that as x x becomes large, the height of the box y y becomes correspondingly small so that x 2 y = 216 . x 2 y = 216 . Similarly, as x x becomes small, the height of the box becomes correspondingly large. We conclude that the domain is the open, unbounded interval ( 0 , ∞ ) . ( 0 , ∞ ) . Note that, unlike the previous examples, we cannot reduce our problem to looking for an absolute maximum or absolute minimum over a closed, bounded interval. However, in the next step, we discover why this function must have an absolute minimum over the interval ( 0 , ∞ ) . ( 0 , ∞ ) .

Step 6: Note that as x → 0 + , x → 0 + , S ( x ) → ∞ . S ( x ) → ∞ . Also, as x → ∞ , x → ∞ , S ( x ) → ∞ . S ( x ) → ∞ . Since S S is a continuous function that approaches infinity at the ends, it must have an absolute minimum at some x ∈ ( 0 , ∞ ) . x ∈ ( 0 , ∞ ) . This minimum must occur at a critical point of S . S . The derivative is

Therefore, S ′ ( x ) = 0 S ′ ( x ) = 0 when 2 x = 864 x 2 . 2 x = 864 x 2 . Solving this equation for x , x , we obtain x 3 = 432 , x 3 = 432 , so x = 432 3 = 6 2 3 . x = 432 3 = 6 2 3 . Since this is the only critical point of S , S , the absolute minimum must occur at x = 6 2 3 x = 6 2 3 (see Figure 4.70 ). When x = 6 2 3 , x = 6 2 3 , y = 216 ( 6 2 3 ) 2 = 3 2 3 in . y = 216 ( 6 2 3 ) 2 = 3 2 3 in . Therefore, the dimensions of the box should be x = 6 2 3 in . x = 6 2 3 in . and y = 3 2 3 in . y = 3 2 3 in . With these dimensions, the surface area is

Checkpoint 4.36

Consider the same open-top box, which is to have volume 216 in . 3 . 216 in . 3 . Suppose the cost of the material for the base is 20 ¢ / in . 2 20 ¢ / in . 2 and the cost of the material for the sides is 30 ¢ / in . 2 30 ¢ / in . 2 and we are trying to minimize the cost of this box. Write the cost as a function of the side lengths of the base. (Let x x be the side length of the base and y y be the height of the box.)

Section 4.7 Exercises

For the following exercises, answer by proof, counterexample, or explanation.

When you find the maximum for an optimization problem, why do you need to check the sign of the derivative around the critical points?

Why do you need to check the endpoints for optimization problems?

True or False . For every continuous nonlinear function, you can find the value x x that maximizes the function.

True or False . For every continuous nonconstant function on a closed, finite domain, there exists at least one x x that minimizes or maximizes the function.

For the following exercises, set up and evaluate each optimization problem.

To carry a suitcase on an airplane, the length + width + + width + height of the box must be less than or equal to 62 in . 62 in . Assuming the base of the suitcase is square, show that the volume is V = h ( 31 − ( 1 2 ) h ) 2 . V = h ( 31 − ( 1 2 ) h ) 2 . What height allows you to have the largest volume?

You are constructing a cardboard box with the dimensions 2 m by 4 m . 2 m by 4 m . You then cut equal-size squares from each corner so you may fold the edges. What are the dimensions of the box with the largest volume?

Find the positive integer that minimizes the sum of the number and its reciprocal.

Find two positive integers such that their sum is 10 , 10 , and minimize and maximize the sum of their squares.

For the following exercises, consider the construction of a pen to enclose an area.

You have 400 ft 400 ft of fencing to construct a rectangular pen for cattle. What are the dimensions of the pen that maximize the area?

You have 800 ft 800 ft of fencing to make a pen for hogs. If you have a river on one side of your property, what is the dimension of the rectangular pen that maximizes the area?

You need to construct a fence around an area of 1600 ft 2 . 1600 ft 2 . What are the dimensions of the rectangular pen to minimize the amount of material needed?

Two poles are connected by a wire that is also connected to the ground. The first pole is 20 ft 20 ft tall and the second pole is 10 ft 10 ft tall. There is a distance of 30 ft 30 ft between the two poles. Where should the wire be anchored to the ground to minimize the amount of wire needed?

[T] You are moving into a new apartment and notice there is a corner where the hallway narrows from 8 ft to 6 ft . 8 ft to 6 ft . What is the length of the longest item that can be carried horizontally around the corner?

A patient’s pulse measures 70 bpm, 80 bpm, then 120 bpm . 70 bpm, 80 bpm, then 120 bpm . To determine an accurate measurement of pulse, the doctor wants to know what value minimizes the expression ( x − 70 ) 2 + ( x − 80 ) 2 + ( x − 120 ) 2 ? ( x − 70 ) 2 + ( x − 80 ) 2 + ( x − 120 ) 2 ? What value minimizes it?

In the previous problem, assume the patient was nervous during the third measurement, so we only weight that value half as much as the others. What is the value that minimizes ( x − 70 ) 2 + ( x − 80 ) 2 + 1 2 ( x − 120 ) 2 ? ( x − 70 ) 2 + ( x − 80 ) 2 + 1 2 ( x − 120 ) 2 ?

You can run at a speed of 6 6 mph and swim at a speed of 3 3 mph and are located on the shore, 4 4 miles east of an island that is 1 1 mile north of the shoreline. How far should you run west to minimize the time needed to reach the island?

For the following problems, consider a lifeguard at a circular pool with diameter 40 m . 40 m . He must reach someone who is drowning on the exact opposite side of the pool, at position C . C . The lifeguard swims with a speed v v and runs around the pool at speed w = 3 v . w = 3 v .

Find a function that measures the total amount of time it takes to reach the drowning person as a function of the swim angle, θ . θ .

Find at what angle θ θ the lifeguard should swim to reach the drowning person in the least amount of time.

A truck uses gas as g ( v ) = a v + b v , g ( v ) = a v + b v , where v v represents the speed of the truck and g g represents the gallons of fuel per mile. Assuming a a and b b are positive, at what speed is fuel consumption minimized?

For the following exercises, consider a limousine that gets m ( v ) = ( 120 − 2 v ) 5 mi/gal m ( v ) = ( 120 − 2 v ) 5 mi/gal at speed v , v , the chauffeur costs $15/h , $15/h , and gas is $ 3.5 / gal . $ 3.5 / gal .

Find the cost per mile at speed v . v .

Find the cheapest driving speed.

For the following exercises, consider a pizzeria that sell pizzas for a revenue of R ( x ) = a x R ( x ) = a x and costs C ( x ) = b + c x + d x 2 , C ( x ) = b + c x + d x 2 , where x x represents the number of pizzas ;   a   >   c ;   a   >   c .

Find the profit function for the number of pizzas. How many pizzas gives the largest profit per pizza?

Assume that R ( x ) = 10 x R ( x ) = 10 x and C ( x ) = 2 x + x 2 . C ( x ) = 2 x + x 2 . How many pizzas sold maximizes the profit?

Assume that R ( x ) = 15 x , R ( x ) = 15 x , and C ( x ) = 60 + 3 x + 1 2 x 2 . C ( x ) = 60 + 3 x + 1 2 x 2 . How many pizzas sold maximizes the profit?

For the following exercises, consider a wire 4 ft 4 ft long cut into two pieces. One piece forms a circle with radius r r and the other forms a square of side x . x .

Choose x x to maximize the sum of their areas.

Choose x x to minimize the sum of their areas.

For the following exercises, consider two nonnegative numbers x x and y y such that x + y = 10 . x + y = 10 . Maximize and minimize the quantities.

x 2 y 2 x 2 y 2

y − 1 x y − 1 x

x 2 − y x 2 − y

For the following exercises, draw the given optimization problem and solve.

Find the volume of the largest right circular cylinder that fits in a sphere of radius 1 . 1 .

Find the volume of the largest right cone that fits in a sphere of radius 1 . 1 .

Find the area of the largest rectangle that fits into the triangle with sides x = 0 , y = 0 x = 0 , y = 0 and x 4 + y 6 = 1 . x 4 + y 6 = 1 .

Find the largest volume of a cylinder that fits into a cone that has base radius R R and height h . h .

Find the dimensions of the closed cylinder volume V = 16 π V = 16 π that has the least amount of surface area.

Find the dimensions of a right cone with surface area S = 4 π S = 4 π that has the largest volume.

For the following exercises, consider the points on the given graphs. Use a calculator to graph the functions.

[T] Where is the line y = 5 − 2 x y = 5 − 2 x closest to the origin?

[T] Where is the line y = 5 − 2 x y = 5 − 2 x closest to point ( 1 , 1 ) ? ( 1 , 1 ) ?

[T] Where is the parabola y = x 2 y = x 2 closest to point ( 2 , 0 ) ? ( 2 , 0 ) ?

[T] Where is the parabola y = x 2 y = x 2 closest to point ( 0 , 3 ) ? ( 0 , 3 ) ?

For the following exercises, set up, but do not evaluate, each optimization problem.

A window is composed of a semicircle placed on top of a rectangle. If you have 20 ft 20 ft of window-framing materials for the outer frame, what is the maximum size of the window you can create? Use r r to represent the radius of the semicircle.

You have a garden row of 20 20 watermelon plants that produce an average of 30 30 watermelons apiece. For any additional watermelon plants planted, the output per watermelon plant drops by one watermelon. How many extra watermelon plants should you plant?

You are constructing a box for your cat to sleep in. The plush material for the square bottom of the box costs $ 5 / ft 2 $ 5 / ft 2 and the material for the sides costs $ 2 / ft 2 . $ 2 / ft 2 . You need a box with volume 4 ft 3 . 4 ft 3 . Find the dimensions of the box that minimize cost. Use x x to represent the length of the side of the box.

You are building five identical pens adjacent to each other with a total area of 1000 m 2 , 1000 m 2 , as shown in the following figure. What dimensions should you use to minimize the amount of fencing?

You are the manager of an apartment complex with 50 50 units. When you set rent at $ 800 / month, $ 800 / month, all apartments are rented. As you increase rent by $ 25 / month, $ 25 / month, one fewer apartment is rented. Maintenance costs run $ 50 / month $ 50 / month for each occupied unit. What is the rent that maximizes the total amount of profit?

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution-NonCommercial-ShareAlike License and you must attribute OpenStax.

Access for free at https://openstax.org/books/calculus-volume-1/pages/1-introduction

• Authors: Gilbert Strang, Edwin “Jed” Herman
• Publisher/website: OpenStax
• Book title: Calculus Volume 1
• Publication date: Mar 30, 2016
• Location: Houston, Texas
• Book URL: https://openstax.org/books/calculus-volume-1/pages/1-introduction
• Section URL: https://openstax.org/books/calculus-volume-1/pages/4-7-applied-optimization-problems

© Feb 5, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

NEOS Server: State-of-the-Art Solvers for Numerical Optimization

The NEOS Server is a free internet-based service for solving numerical optimization problems. Hosted by the Wisconsin Institute for Discovery at the University of Wisconsin in Madison , the NEOS Server provides access to more than 60 state-of-the-art solvers in more than a dozen optimization categories. Solvers hosted by the University of Wisconsin in Madison run on distributed high-performance machines enabled by the HTCondor software ; remote solvers run on machines at Arizona State University , the University of Klagenfurt in Austria, and the University of Minho in Portugal.

The NEOS Guide website complements the NEOS Server, showcasing optimization case studies , presenting optimization information and resources , and providing background information on the NEOS Server.

NEOS Server

• Submit a job to NEOS
• View Job Queue and Job Results
• User's Guide to the NEOS Server
• NEOS Server FAQ
• NEOS Support
• NEOS Case Studies
• NEOS Optimization Guide
• NEOS Server Information
• Optimization Resources

Advanced Tools

• Statistics: solvers , websites
• Job Archives (password required)
• Downloads: Client Tools ( GitHub ) and Kestrel

• Academic Journals
• Books & Monographs
• Conferences
• Standard Editing Service
• Expert Scientific Editing Services
• Academic Translation Service
• News & Announcements

Table of Content

• Introduction
• Related Works
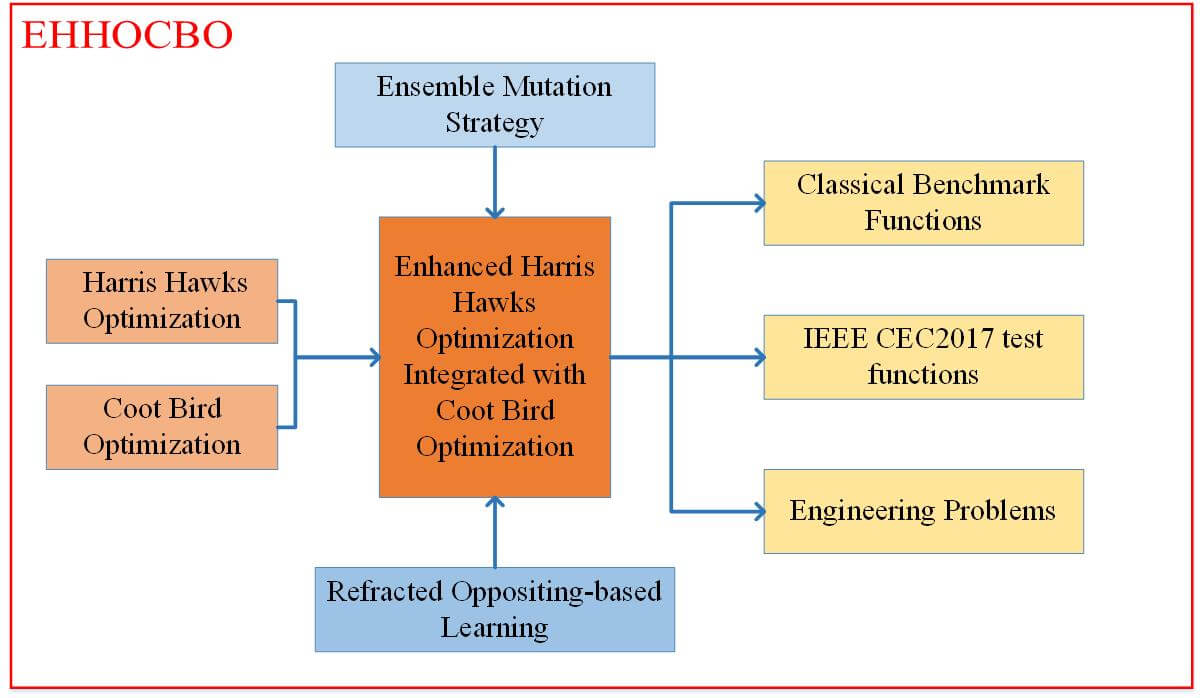
• The Proposed EHHOCBO Algorithm
• Experimental Results and Discussions
• EHHOCBO for Addressing Engineering Problems
• Conclusion and Future Directions

Enhanced Harris Hawks Optimization Integrated with Coot Bird Optimization for Solving Continuous Numerical Optimization Problems

Hao Cui , Yanling Guo * , Yaning Xiao , Yangwei Wang * , Jian Li , Yapeng Zhang , Haoyu Zhang

College of Mechanical and Electrical Engineering, Northeast Forestry University, Harbin, 150040, China

(This article belongs to the Special Issue: Bio-inspired Computer Modelling: Theories and Applications in Engineering and Sciences )

Computer Modeling in Engineering & Sciences 2023 , 137 (2), 1635-1675. https://doi.org/10.32604/cmes.2023.026019

Received 10 August 2022; Accepted 30 January 2023; Issue published 26 June 2023

Graphical Abstract

Cite This Article

• Full-Text PDF
• Full-Text HTML
• Full-Text XML
• Full-Text Epub

Related articles

A Pathway to Explore the Hidden Specialty in the Design of Fifteen Level Inverter in Grid Connected PV System

The Reduced Space Method for Calculating the Periodic Solution of Nonlinear Systems

A Novel Interacting Multiple-Model Method and Its Application to Moisture Content Prediction of ASP Flooding

A New Hybrid Uncertain Analysis Method and its Application to Acoustic Field with Random and Interval Parameters

Computation of Aerodynamic Noise Radiated From Open Propeller Using Boundary Element Method

Further Information

About Tech Science Press

Open Access Policy

Article Processing Charges

Special Issue Policy

Research Topic Policy

Terms and Conditions

Privacy Policy

Advertising Policy

Contact TSP

For Editors

For Reviewers

For Authors

For Conference Organizers

For Subscribers

Join TSP editorial community

• {{subColumn.name}}

AIMS Mathematics

• {{newsColumn.name}}
• Share facebook twitter google linkedin

A new filled function method based on global search for solving unconstrained optimization problems

• Jia Li 1 , 
• Yuelin Gao 2 ,  ,  , 
• Tiantian Chen 1 , 
• Xiaohua Ma 2
• 1. School of Mathematics and Information Sciences, North Minzu University, Yinchuan 750021, China
• 2. Ningxia province cooperative innovation center of scientific computing and intelligent information processing, North Minzu University, Yinchuan 750021, China
• Received: 09 April 2024 Revised: 22 May 2024 Accepted: 29 May 2024 Published: 03 June 2024

MSC : 90C26, 90C30

• Full Text(HTML)
• Download PDF

The filled function method is a deterministic algorithm for finding a global minimizer of global optimization problems, and its effectiveness is closely related to the form of the constructed filled function. Currently, the filled functions mainly have three drawbacks in form, namely, parameter adjustment and control (if any), inclusion of exponential or logarithmic functions, and properties that are discontinuous and non-differentiable. In order to overcome these limitations, this paper proposed a parameter-free filled function that does not include exponential or logarithmic functions and is continuous and differentiable. Based on the new filled function, a filled function method for solving unconstrained global optimization problems was designed. The algorithm selected points in the feasible domain that were far from the global minimum point as initial points, and improved the setting of the step size in the stage of minimizing the filled function to enhance the algorithm's global optimization capability. In addition, tests were conducted on 14 benchmark functions and compared with existing filled function algorithms. The numerical experimental results showed that the new algorithm proposed in this paper was feasible and effective.

• unconstrained global optimization ,
• filled function method ,
• global minimizer ,
• parameter-free ,
• step size setting

Citation: Jia Li, Yuelin Gao, Tiantian Chen, Xiaohua Ma. A new filled function method based on global search for solving unconstrained optimization problems[J]. AIMS Mathematics, 2024, 9(7): 18475-18505. doi: 10.3934/math.2024900

Related Papers:

• This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->

Supplements

Access history.

• Corresponding author: Email: [email protected] ; 

Reader Comments

• © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )

通讯作者: 陈斌, [email protected]

沈阳化工大学材料科学与工程学院 沈阳 110142

Article views( 42 ) PDF downloads( 8 ) Cited by( 0 )

Figures and Tables

Tables( 10 )

Associated material

Other articles by authors.

• Tiantian Chen

Related pages

• on Google Scholar
• Email to a friend
• Order reprints

Export File

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

• View all journals
• My Account Login
• Explore content
• About the journal
• Publish with us
• Sign up for alerts
• Open access
• Published: 28 May 2024

Quantum computing for several AGV scheduling models

• Liang Tang 1 ,
• Chao Yang 1 ,
• Kai Wen 2 ,
• Wei Wu 3 &
• Yiyun Guo 4  

Scientific Reports volume  14 , Article number:  12205 ( 2024 ) Cite this article

452 Accesses

1 Altmetric

Metrics details

• Applied mathematics
• Computer science
• Quantum physics

Due to the high degree of automation, automated guided vehicles (AGVs) have been widely used in many scenarios for transportation, and traditional computing power is stretched in large-scale AGV scheduling. In recent years, quantum computing has shown incomparable performance advantages in solving specific problems, especially Combinatorial optimization problem. In this paper, quantum computing technology is introduced into the study of the AGV scheduling problem. Additionally two types of quadratic unconstrained binary optimisation (QUBO) models suitable for different scheduling objectives are constructed, and the scheduling scheme is coded into the ground state of Hamiltonian operator, and the problem is solved by using optical coherent Ising machine (CIM). The experimental results show that compared with the traditional calculation method, the optical quantum computer can save 92% computation time on average. It has great application potential.

Similar content being viewed by others

DNA as a perfect quantum computer based on the quantum physics principles

A vision chip with complementary pathways for open-world sensing

About feasibility of SpaceX's human exploration Mars mission scenario with Starship

Introduction.

The scale of the logistics industry has maintained a considerable growth rate, and many human and material resources have been invested in it, thus creating the labor-intensive industry. Improving the automatic and intelligent level of the logistics industry has become an important issue for industry and academia. In recent years, some of the industry’s leading enterprises have already carried out technological reforms. For example, the retail giant, Amazon, has established a huge logistics center, that uses intelligent sorting technology, delivery drones, automated guided vehicles (AGVs), etc. China’s e-commerce giant, Jingdong, has also set up an ‘Asia One’ warehouse, in which more than 100 AGVs are used for transportation operations at the same time 1 . In addition, technical innovation also occurred in ports. In 1993, the world’s first automated wharf was built in the Amsterdam Port in the Netherlands, and dozens of AGVs were used for container transshipment. With the introduction of technology and the accumulation of operation experience, the construction of automatic terminals has been tried all over the world, and the usage of AGVs has gradually increased. Currently, the use of AGVs has penetrated all aspects of logistics, transportation and production, which has greatly promoted the level of industrial automation and intelligence and improved efficiency.

To meet the needs of application scenarios, the amount of parallel work of AGVs is increasing, which brings great difficulty to the AGV scheduling. AGV scheduling problem is a difficult combinatorial optimization problem, and a large number of researchers have devoted themselves to this field and made some contributions. Singh et al. 2 considered AGV scheduling with battery constraints, developed a mixed-integer programming model with the objective of minimizing the combined task delay cost and AGV transportation cost, and designed a customized adaptive large-neighborhood search algorithm to solve the model. Zhang et al. 3 studied an AGV scheduling problem in matrix manufacturing plants, and proposed a mixed integer programming model to minimize the generalized transportation cost, based on which an improved iterative greedy algorithm was designed and compared with six other algorithms to show its superior solution performance. For the scheduling problem of AGVs in smart factories, Zhang et al. 4 proposed a self-organized dynamic scheduling method, that groups multiple AGVs to perform tasks among themselves and uses improved gene expression programming to learn dynamic scheduling rules. The numerical experimental results show that the method can considerably reduce system costs. Wang and Zeng 5 studied the port AGV scheduling and path planning problem under conflict-free paths, established a mixed integer model with the objective of minimizing task completion time, and proposed a customized branch and bound algorithm combined with a heuristic algorithm to solve the small-scale problem, and further developed a two-stage greedy heuristic algorithm to quickly obtain a satisfactory solution for the large-scale problem. Sagar and Jerald 6 proposed a real-time scheduling strategy for AGVs based on deep reinforcement learning technology, established a Markov decision model for real-time scheduling, and developed a Q-learning algorithm. The superiority of the method is shown through numerical experiments. Considering the scheduling and path planning model of shop floor AGVs, Saidi et al. 7 developed a discrete-time model and proposed a two-stage ant colony algorithm to solve the model. From the above literature, the research on scheduling problems of AGVs covers several scenarios such as workshops and terminals. Researchers have built mixed integer programming models, integer programming models, Markov decision process models, etc. The methods used are scheduling rules, exact algorithms, heuristic algorithms, reinforcement learning algorithms, etc. From the results, it is observed that the exact algorithm can generate optimal scheduling solutions, however, its computational time is prohibitively slow, rendering it impractical for large-scale problems. Inexact algorithms exhibit favorable efficiency but often converge to local optima. The provision of high-quality scheduling solutions within a short timeframe poses a significant challenge.

In recent years, significant advancements have been made in both theoretical understanding and practical applications of quantum computing. The fundamental distinction between quantum computers and traditional computers lies in their reliance on quantum mechanical principles. Quantum computers utilize quantum bits (qubits) as the fundamental units of information storage 8 , which can exist in superposition states of both 1 and 0, enabling them to hold exponentially more information compared to traditional computers. It is well recognized that quantum computers offer substantial advantages, particularly in addressing specific problems such as combinatorial optimization, often described as the superiority of quantum computing. Many combinatorial optimization problems are NP-hard, presenting significant challenges for traditional computers to solve. Combinatorial optimization problem can be mapped to the ground state search problem of Ising model. Hardware systems can be built in many different ways to simulate the process of Hamiltonian reduction, such as adiabatic quantum computing (AQC), quantum annealing (QA), etc. However, it is always a difficult problem to improve the connection density between qubits, which will affect the efficiency of problem solving 9 , 10 . Coherent Ising Machine (CIM) is a quantum computer developed according to the optical principle 11 , 12 , 13 , 14 , 15 , 16 , 17 , which can work at room temperature and deal with large-scale problems, such as compression sensor problems 18 and polyhedron problems 19 . CIM uses laser pulses in optical fiber as qubits for quantum calculation. The early prototype of CIM is injection synchronous laser Ising machine. The number of coupled lasers in this scheme is proportional to the square of qubits, which is quite difficult. On this basis, optical delay linear CIM and measurement feedback CIM using nonlinear optical crystal instead of laser are developed. The latter uses measurement feedback to avoid the challenge that the former needs to control a large number of optical delay lines accurately 14 . The machine used in this study is measurement feedback CIM.

AGV scheduling problem can be understood as a kind of routing problem. Most traditional solutions to routing problems require sacrificing large amounts of computational resources and Osaba et al. 20 indicated that quantum computing techniques have great potential in the area of solving routing and optimization problems. In the early days, Goswami et al. 21 developed a phase estimation technique to solve the traveling salesman problem (TSP), using IBM’s quantum simulator to provide results for four city cases. Then, researchers tried to solve more complex problems with quantum computing. Feld et al. 22 presented a quadratic unconstrained binary optimization (QUBO) formulation for solving the vehicle routing problem with capacity constraints, evaluated the solution quality and computation time and compared it with classical solution methods. Bao et al. 23 proposed a two-stage QUBO formulation of the vehicle routing problem with balanced pickup, mapping the first stage to a clustering problem and describing the second stage as a TSP problem, and evaluated it against traditional methods in terms of numerical experimental results. Harwood et al. 24 tried to establish a qubo model to describe the vehicle routing problem by using the modeling idea of node and arc, and evaluated the model by using analog quantum devices. Geitz et al. 25 built a QUBO model to solve the job-shop scheduling problem, using quantum computers or simulators, constrained programming and tabu search. The calculation results proved the effectiveness of quantum computing in small-scale situations. And the established QUBO model can be extended to AGV scheduling problem. Ohzeki et al. 26 formulated an Ising model for the collision-free scheduling problem of AGVs within a factory setting. They utilized a quantum annealing machine to solve the model, with results demonstrating the potential application of quantum annealing machines in addressing real-world industrial challenges. Based on the above cases, it can be seen that some researchers have begun to use quantum computing to solve practical problems in the field of optimization. However, the research on quantum computing related to AGV scheduling has just started, and many researchers used simulators to solve them, because the current physical real machine resources are scarce, and the scale of solving problems is still relatively small, and it is easy to make mistakes and lacks the running data of physical real machines.

Our contributions

In a word, most of the existing AGV scheduling research adopts traditional models and methods, which can not effectively meet the actual needs of large-scale scheduling. Quantum computing has great application potential in solving specific problems that traditional computers cannot solve, and researchers have tried in optimization fields. However, as far as we know, there are few literatures about AGV scheduling using quantum computing technology. Based on these facts, the idea of carrying out this research came into being. The main contributions of this paper are summarized as follows.

In traditional research on the AGV scheduling problem, the computation time increases greatly with an increase in the number of AGVs and tasks. We introduce quantum computing technology into the research of the AGV scheduling problem and construct new QUBO models of AGV scheduling. In real scenarios, dispatchers often set different scheduling objectives according to the nature of the work, among which minimizing the total AGV travel time and minimizing the task completion time (makespan) are the two most common objectives. According to the different objectives, we have deduced different QUBO models, and given the model solutions and related theoretical basis under two different objectives.

We use traditional computer and CIM to carry out numerical experiments on the traditional model and QUBO model proposed by us respectively. The experimental results show that the computation speed of CIM is much faster than that of traditional computer, and the average calculation time is saved by 92%, which proves that CIM has great application potential in solving AGV scheduling problem and similar combinatorial optimization problems.

AGV scheduling model

AGV scheduling problems have many classifications according to different scenarios and considerations. For example, consider the time window of the task, joint optimization of scheduling and path, cooperation with other devices, charging strategy and so on. Due to the limitation of quantum bits of CIM, it is impossible to solve the AGV scheduling problem in complex scenes 27 , 28 , 29 . Therefore, we simplify the problem and keep the essence of AGV scheduling problem. On this basis, we construct the AGV scheduling model. In this section, we present the classical AGV scheduling model based on mixed integer programming (MIP), and propose two new models, which we call the node and arc models.

Problem description

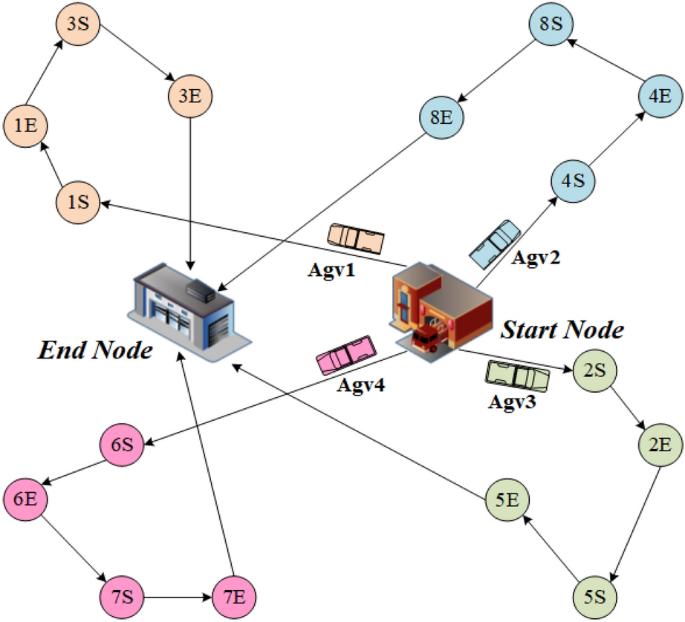
The AGV scheduling problem and a feasible solution. All AGVs start from a fixed start node, perform transportation tasks, and reach the end node after performing all tasks. ’S’ represents the starting point of a transportation task, and ’E’ represents the end point of a transportation task. Different colors represent different AGV’s mission routes.

We consider an AGV scheduling problem (to make the problem more general, we do not set up a working scenario), as shown in Fig.  1 . Given an AGV set, all AGVs have a unified starting node and ending node, and all AGVs start to accept tasks from the unified starting node until all transportation tasks are completed, and then return to the unified ending node. In the AGV scheduling problem, we are given a set of transportation tasks, each with a starting point and an ending point. For an AGV, the process of completing the transportation task can be described as first arriving at the starting point of the task to load the transported goods, then transporting them to the ending point of the task, and then driving to the starting point of the next task to perform the next task. The travel time of the AGV between any two task points is known. We consider two optimization objectives, the first is to minimize the total AGV travel time and the second is to minimize the maximum task completion time (makespan). The first objective is generally used when the task is not urgent to achieve a reduction in total system energy consumption, while the second objective is set to complete transportation tasks quickly.

Next, we elaborate on the symbolic settings in the problem as follows.

\(V=\{1,\ldots ,k,\ldots ,K \}\) set of AGVs,

\( R=\{1,\ldots ,r,{{r}^{'}},{{r}^{''}},\ldots ,n-1 \}\) set of actual tasks,

\({{R}_{1}}=\{0,1,\ldots ,r,{{r}^{'}},{{r}^{''}},\ldots ,n-1\}\) set of actual tasks and virtual start task,

\({{R}_{2}}=\{1,\ldots ,r,{{r}^{'}},{{r}^{''}},\ldots ,n\}\) set of actual tasks and virtual end task,

\({{R}^{'}}=\{0,1,\ldots ,r,{{r}^{'}},{{r}^{''}},\ldots ,n\}\)  set of all tasks,

\(A=\{(r,{{r}^{'}})\mid r,{{r}^{'}}\in {{R}^{'}}\}\) arc set that consists of all valid task pairs that can be conducted adjacently,

\(\pi =\{1,\ldots ,t,\ldots ,N \}\) set of the sequence of tasks performed by an AGV

a        a single task arc

\(\theta _{r}^{+}\)      an arc with task r as the left node

\(\theta _{r}^{-}\)      an arc with task r as the right node

\(r_{\text{s}}\)       starting point of task r ,

\(r_{\text{d}}\)       ending point of task r .

\({{e}_{{{r}_\text{s}}{{r}_\text{d}}}}\)     indicates the travel time of the AGV from two points \({{r}_\text{s}}\) and \({{r}_\text{d}}\) ,

\({{e}_{{{r}_\text{d}}r_\text{s}^{'}}}\)     indicates the travel time of the AGV from two points \({{r}_\text{d}}\) and \(r_\text{s}^{'}\) ,

\({{c}_{r{{r}^{'}}}}\)      contains two parts of time, the first part is the time from the start of task r to the end of task r , and the second part is the time from the end of task r to the start of task \({r}^{'}\) , \({{c}_{r{{r}^{'}}}}={{e}_{{{r}_{s}}{{r}_{d}}}}+{{e}_{{{r}_{d}}r_{s}^{'}}}\) .

Mixed integer programming model

In this subsection, we introduce the classical model of AGV scheduling. The classical model is formed as a mixed integer programming, and it has the following variables.

\({{y}_{r,{{r}^{'}},k}}\)       binary variable, equal to 1 if task r is performed directly prior to \({{r}^{'}}\) by AGV k , 0 otherwise;

\(f^\text{s}_{rk}\)          arrival time of AGV k at the start node of task r ;

\(f^\text{d}_{rk}\)          arrival time of AGV k at the end node of task r ;

T           the makespan for AGVs to perform transportation tasks.

The first optimization objective of the MIP model is to minimize the total AGV travel time, and its model is presented as follows.

The objective function ( 1 ) is to minimize the total travel time of the AGV. Constraints ( 2 ) and ( 3 ) ensure that all AGVs need to complete the virtual start task and the virtual end task, and constraints ( 4 ) guarantee that all actual tasks are uniquely assigned to a particular AGV. Constraints ( 5 ) ensure that each AGV completes its task satisfying the flow balance. Then, constraints ( 6 ) guarantee that the virtual start task starts and ends at moment 0. Constraints ( 7 ) states that the time to reach the end of a task is equal to the time to reach the start of that task plus the transport time from the start to the end. Constraints ( 8 ) indicates that the time to reach the start of a task is later than the time to reach the end of the previous task plus the transportation time required to reach the start of that task from the end of the previous task, where M is a sufficiently large value. The last constraints ( 9 ) eliminates task self-citation. Constraints ( 10 ) and ( 11 ) represent range limits of variables.

A slight modification of the above model can be used as a model for minimizing the makespan for AGVs to perform transportation tasks, which is given as follows, Eqs. ( 2 )–( 11 ).

where T denotes the makespan. The objective function is to minimize T , and constraints ( 13 ) denotes that T must be no less than the time required by the last AGV to complete the task.

QUBO and Ising model

This section mainly describes the concepts of QUBO model and Ising model and their relationship. QUBO is an expression of optimization problem, and its goal is to find binary variables that minimize quadratic polynomials. Ising model was first put forward and applied in statistical physics. It describes a system composed of interacting units, in which each spin particle must have two possible random states (such as + 1 and − 1), and then it was introduced into the field of mathematics as a model to describe a series of optimization problems. Many combinatorial optimization problems can be expressed in the form of quadratic unconstrained binary optimization or ising model, and they can be transformed into each other 30 , 31 , 32 . The general expression of QUBO model is shown in Eq. ( 14 ).

where x is a z dimensional vector of binary variables, Q is the quadratic coefficient matrix, and \({{c}^\texttt{T}}\) is the coefficient matrix of the primary term.

The above model in the form of QUBO can be easily transformed into an Ising model, and the variable range of the Ising model is \(\left\{ -1,1 \right\} \) . Specifically, it can be realized by variable substitution \({{\sigma }_{i}}=2{{x}_{i}}-1\) . Then, the optimization function can be expressed in the following form.

where the \({{\sigma }_{i}}\) is spin variable, \({{J}_{ij}}\) and \({{h}_{i}}\) are the quadratic and linear coefficients. The solution of Ising problem is to find the ground state of Hamiltonian. CIM solves the Ising problem according to the principle of minimum gain, and can find the ground state or low energy state of Ising Hamiltonian. The method is to map the QUBO problem into a fully connected Ising Hamiltonian with programmable parameters, and obtain the solution of the problem through controllable quantum phase transition 33 , 34 .

In this section, we will describe the node model. The core idea of node model is to regard tasks as nodes and the order of task execution as the order of vehicles passing through nodes.The node model has the QUBO form and is suitable for quantum computing, the variables of the model are described as below.

\({{x}_{r,t,k}}\) binary variable, equal to 1 if task r is assigned to AGV k as it is t -th task, 0 otherwise.

The first optimization objective of the node model is to minimize the total AGV travel time, and the model is shown below.

\({{\partial }_{i}}\) \((i=1,\ldots ,6)\) are weights correspond to each objective function. The objective function ( 17 ) is to minimize the total travel time of all the AGVs. The minimization function ( 18 ) and ( 19 ) ensures that for each AGV, the virtual start task and the virtual end task must be the first task and the last task, respectively. For each actual task, we want it to be assigned exactly to one AGV, so we add the minimization function ( 20 ). We also consider the minimization function ( 21 ) in order to make each AGV perform at most one task on each task sequence. For a particular AGV, the order of its tasks must be continuous, based on which we set the minimization function ( 22 ).

The model described below is modified from the above model to accommodate the goal of minimizing the makespan.

The least time-consuming task model requires finding the AGV with the longest task execution time and minimizing its execution task time, which leads to inequality constraints, as follows.

The objective function ( 24 ) is to minimize the makespan T .

Then we add slack variables to transform the above inequality constraint into an equation, as follows.

\({{T}_{k}}\) \((k\in V)\) is the slack variable, and both T and \({{T}_{k}}\) \((k\in V)\) need to be represented by binary variables. \({{\delta }_{i}}\) \( (i=1,2,\ldots ,m)\) and \({{\delta }_{ik}}\) \((i=1,2,\ldots ,{m}^{'}, {k}\in {V})\) are the discretized auxiliary variables we introduce, whose number is related to the size of the arithmetic case and needs to be estimated. A large number of auxiliary variables will make the difficulty of solving soar. In general, to represent an integer between 0 and \(\varsigma \) , \(\left[ {{\log }_{2}} \varsigma \right] +1\) discretized auxiliary variables need to be introduced, where \([\varsigma ]\) denotes the largest integer that does not exceed \(\varsigma \) . Of course, if there are non-integer values introduced in the calculation example, then it is necessary to introduce an approximate representation. First, we introduce the precision matrix as follows:

Then the real numbers \({{\varpi }_{i}}\) \((i=1,\ldots ,L)\) in some interval can be approximated as follows.

where \({{b}_{i}}\in {{\{0,1\}}^{L}}\) \((i=1,\ldots ,L)\) . If the error is expressed in terms of \(\phi \) , the error satisfies the following relation:

In this way, we can rewrite ( 24 ) and ( 25 ) as follows.

The positive real numbers can be approximated using integer auxiliary variables. \({{\sigma }_{j}}\) \((j=1,2\ldots ,L)\) and \({{\sigma }_{jk}}\) \((j=1,2,\ldots ,{{L}^{'}},k\in V)\) are used to approximate the decimal part. The number of binary variables used is related to the required approximate accuracy, as shown in Formula ( 28 ).

Thus, the model under this objective can be represented as follows, Eqs. ( 18 )–( 22 ), ( 24 )–( 25 ), ( 31 )–( 32 ).

In ( 33 ), \({{\varepsilon }_{i}}\) \((i=1\ldots ,7)\) are weights for each objectives. The model does not satisfy the QUBO form, because \({{H}_{Z}}\) is a quadrinomial binary polynomial, which needs to be degenerated. Next, we provide some analysis of the \({{H}_{Z}}\) . First, to make it easier to show our results, we perform a variable substitution, as follows:

The total number of tasks is N , and \(\eta \) contains \(({{N}^{2}}-3N+3)(N-1)\) monomials. Then \({{H}_{Z}}\) can be expanded as follows.

In the \({{H}_{Z}}\) , \({{\eta }^{2}}\) is a quadrinomial binary polynomial, \(-2\eta T\) and \(2\eta {{T}_{k}}\) are cubic binary polynomials, and \({{T}^{2}}\) , \(T_{k}^{2}\) and \(-2T{{T}_{k}}\) are all quadratic binary polynomials, so we need to reduce \({{\eta }^{2}}\) , \(-2\eta T\) and \(2\eta {{T}_{k}}\) . The number of quardrinomial binary monomials in \({{\eta }^{2}}\) is represented by \({{\tau }_{4}}\) , and \({{\tau }_{4}}\) is as follows:

where \({{\mathbb {Z}}^{+}}\) represents the set of all positive integers. Equation ( 37 ) indicates that any power of the binary variable itself is equal to itself, and thus, \(\tau _{4}^{'}\) quardrinomial monomial can be directly reduced, and its specific number is as follows.

Therefore, the number of quadrinomial polynomials that truly need to be reduced is \({{\tau }_{4}}-\tau _{4}^{'}\) terms. Looking at the part of cubic polynomial, the number of cubic monomials in \({{H}_{Z}}\) is represented by \({{\tau }_{3}}\) , and then \({{\tau }_{3}}\) is as follows:

Then, the number of all polynomials in \({{H}_{Z}}\) that need to be descended \(\tau \) is as follows:

At least \(\tau \) binary auxiliary variables must be introduced to complete the descending order according to a paper 35 . Due to the number of auxiliary variables introduced, the processing is more complex and it is difficult to calculate using existing quantum computers. So this model will not be introduced so far in this paper.

In this section we will describe the arc model. The core idea of arc model is that the sequence of tasks before and after execution is regarded as an arc connected between nodes, and building the model with arc as the basic unit can reduce the dimension. The arc model also has a QUBO form with the same parameter settings as the node model, and the decision variables are shown below.

\({{\upsilon }_{a,t,k}}\) binary variable, equal to 1 if arc a is assigned to AGV k in sequence t , 0 otherwise.

As with the node model, we first explore the model with the optimization objective of minimizing the total travel time.

\({{\beta }_{i}}\) \((i=1,\ldots ,8)\) are weights for the corresponding objective. The objective function ( 42 ) is to minimize the total travel time of the AGV. We want all AGVs to be executed in the first order a task arc that starts with a virtual start task, so we add the minimization function ( 43 ). The minimization function ( 44 ) means that the last task completed by each AGV must be a virtual end task. We want to complete at most one task arc in a certain order of an AGV, so we add the minimization function ( 45 ). The minimization function ( 46 ) indicates that for each actual task, we want a certain task arc with it as the starting node to be assigned to an AGV in a certain order of completion, and we want the virtual start task to be completed only once for each AGV, so we add the minimization function ( 47 ). Similarly, for each AGV, its virtual end task can only be completed once, so we add the minimization function ( 48 ). The minimization function ( 49 ) ensures that for each AGV, it is must to satisfy the flow balance when performing the task arc.

Next, we show a model with the goal of minimizing the makespan as follows, Eqs. ( 42 )–( 49 ).

Numerical experiments

In this section, we provide rich numerical experimental results, and research data can be obtained on public databases 36 . In the first subsection we use Gurobi 37 solver to solve the MIP model proposed above on a traditional computer, and show its computing performance under different problem scales. In the second subsection we use optical quantum computer to solve the problem cases of node model and arc model at different scales. And the computation performance is compared with that of traditional computers.

The CIM we used is provided by Beijing Qboson Quantum Technology Co.Ltd, and its structure and principle diagram are shown in Fig.  2 . The components of this CIM are mainly composed of optical parts and electrical parts. The optical part of the machine is composed of pulsed laser, erbium-doped fiber amplifier(EDFA), fiber rings and periodically poled lithium niobate (PPLN) crystals, while the electrical part is mainly composed of optical balanced homodyne detectors (BHD), analog-to-digital/digital-to-analog (AD/DA) converter and field-programmable gate array (FPGA). The laser emits laser with a repetition frequency of 100mhz, which is amplified by EDFA, and then the amplified laser frequency is doubled by PPLN crystal to generate 780 nm laser, which is used as the pump source to synchronously pump the phase sensitive amplifier, forming degenerate optical parametric oscillation(DOPO). There are 211 oscillation pulses in the fiber ring, and the time interval between adjacent pulses is 10 ns, so the transmission time of optical pulses in the ring is 2.11 µs. Then, the laser output in the fiber ring and the laser with the fundamental frequency of 1560 nm are determined by BHD, and the FPGA obtains the feedback signal of the next round trip according to the interaction intensity between spins in Ising Hamiltonian, which is used as the control signal of the intensity modulator (IM), and its sign defines the phase shift (0 or \(\pi \) ) of the phase modulator (PM) 9 , 14 , 34 , 38 .

To compare the performance between CIM and traditional computer, we also run our experiments with Gurobi 9.5.1 on a Mechrevo computer with 2.8 GHz Intel Core i7 CPU and 8GB memory, using up to four threads. The task points used in this experiment are randomly selected on the two-dimensional axis, ranging from 10 to 90, and then Euclidean distance is used as the length between two points, and we design the speed of each AGV to be constant, the time passing through the unit distance is the unit time.

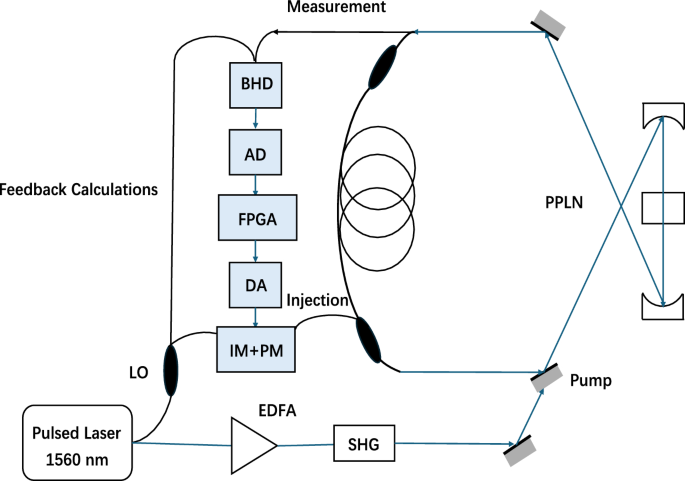
Schematic diagram of coherent Ising mechanism construction and principle.

Computing on a traditional PC

In this section, we use Gurobi to solve the mixed integer programming model of AGV scheduling for two optimization objectives. In “ Number of tasks ” we show experiments on the variation in computation time with the number of tasks, while in “ Number of AGVs ” we show experiments on the variation in computation time with the number of AGVs. We set a time limit to 1800 seconds for each run.

Number of tasks

In general, an increase in the number of tasks leads to a slower generation of AGV scheduling solutions. In this subsection, we investigate the effect of task number variation on the computational speed of the three models proposed in this paper. To achieve this goal, we generate instances of 4 tasks to 12 tasks with a fixed number of AGVs of 2 and obtain the computational time graphs shown in Fig.  3 , where the left figure takes the minimum total travel time as the objective function, and the right figure takes the minimum makespan as the objective function. The legend section represents the model number, which corresponds to the previous section number.

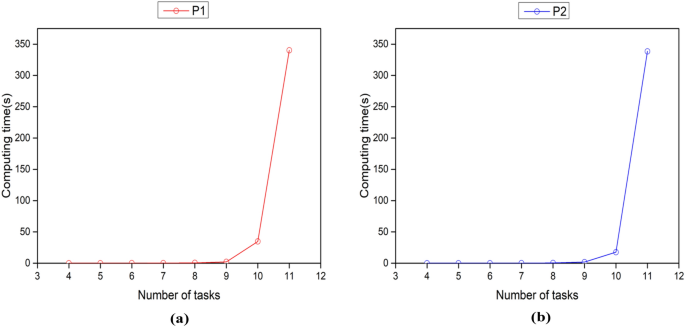
Computation time versus number of tasks for MIP model. ( a ) Represents the change of MIP model computation time with the number of tasks under the goal of minimizing the total travel time. ( b ) Represents the change of MIP model computation time with the number of tasks under the goal of minimizing the makespan.

In Fig.  3 , we find that the computing speed of mixed integer programming model gradually slows down with the increase of the number of AGV tasks, and the computation time increases sharply when the number of tasks reaches a certain critical value, which is a common property reflected by two different objective functions. Especially when the number of tasks increases to 12, the computing time has exceeded 1800s, which reflects the weakness of traditional models in the face of large-scale problems.

Number of AGVs

In this subsection, we hope to explore the influence of the change of AGV number on the computing time of mixed integer programming model, so we fixed the number of tasks as 10 and 11, and set the number of AGVs in the range from 2 to 8. We show the results in Tables  1 and  2 . Notation “–” in the table implies that the corresponding model failed to obtain an optimal solution within the time limit. An instance with a tasks and b AGVs are denoted by “a–b”.

From the results obtained in Tables  1 and  2 , we can conclude that there is no strict correlation between the number of AGV and the computing time. Table  1 shows the computational performance of the three models under the objective of minimize the total travel time, and we can observe that the computational performance of the MIP model is very poor, and many groups of experiments failed to obtain an optimal solution within the limited time. Table   2 shows the computational performance of the MIP model under the objective of minimize the makespan, and the model performs much better, the optimal solution is obtained in the limited time in all groups of experiments. However, its computation time is still at a great disadvantage.

Computational experiment on CIM

In this subsection, we use the CIM to solve the QUBO model and compare its performance with the MIP solver on traditional PC. Since the maximum number of Quantum bits of the CIM used in this research is 100, all the comparative examples in this section limit the number of variables to 100. Based on this, we completed six groups of computation experiments with a quantum computer. In all the experiments, the number of AGV was limited to two. For the numerical experiment of node model, we set the number of tasks to 4 to 7, while for the numerical experiment of arc model, we fixed the number of tasks to 4.

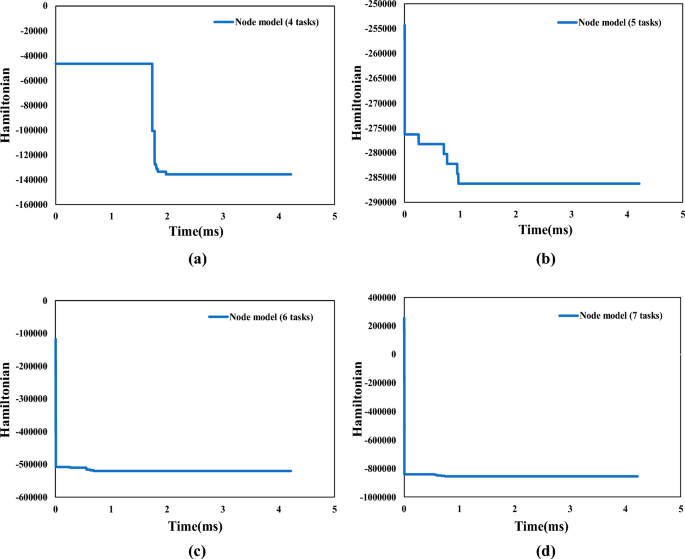
Evolution diagram of Hamiltonian with time under the objective functions of minimizing the total travel time in node model. ( a ) Represents the evolution diagram of Hamiltonian with time under the example of 4 tasks. ( b ) Represents the evolution diagram of Hamiltonian with time under the example of 5 tasks. ( c ) Represents the evolution diagram of Hamiltonian with time under the example of 6 tasks. ( d ) Represents the evolution diagram of Hamiltonian with time under the example of 7 tasks.

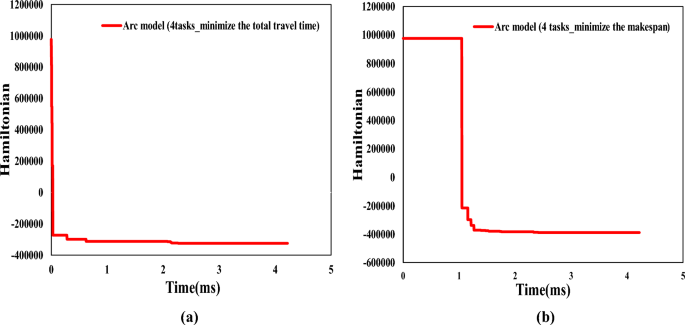
Evolution diagram of Hamiltonian with time under two objective functions of arc mode. ( a ) represents the evolution diagram of Hamiltonian with time under the objective function of minimizing the total travel time. ( b ) Represents the evolution diagram of Hamiltonian with time under the objective function of minimizing the makespan.

In Figs.  4 and   5 , we plot the evolution of Ising Hamiltonian with time under node model and arc model, respectively. According to the above explanation of CIM principle construction, we can know that the time interval between every two adjacent data points in the figure is 2.11 microseconds. The Hamiltonian decreases with the passage of time, and the phase transition occurs as the power of the pump light gradually increases to the oscillation threshold. The solution obtained when reaching the lowest energy state is the result of CIM solution, and the corresponding time at this time is the computation time.

Schematic diagram of quantum computing solutions for node model. ( a ) represents solution under 4 tasks. ( b ) represents solution under 5 tasks. ( c ) represents solution under 6 tasks. ( d ) represents solution under 7 tasks.

Schematic diagram of quantum computing solutions for arc model. ( a ) represents the solution of 4 task under the objective function of minimizing the total time. ( b ) represents the solution of 4 task under the objective function of minimizing the makespan.

Figures  6 and 7 show the schematic diagrams of CIM’s solution under node model and arc model. Among them, Fig.  6 contains four parts, which respectively represent the schematic diagrams under 4-7 tasks, while Fig.  7 contains two parts, which respectively represent the schematic diagrams of solving two objective functions under 4 tasks. In fact, Ising model can be transformed into the corresponding representation of maximum cut problem 15 . The maximum cut problem is usually used as a measure and demonstration basis for the complexity of quantum computing problems and the distribution of solutions. The figure shows the solution of our problem expressed by the representation method of maximum cut problem. Points with different colors indicate that they are in different groups, and the connecting lines of points in the same group are gray, while those of points in different groups are red. In these figures, we can clearly perceive the complexity of each model at different scales.

Here, we compare the performance of node model and arc model on quantum computer with that of mixed integer programming model on traditional computer, and the comparison results are shown in Table  3 . An instance with a tasks and b AGVs are denoted by “a–b”.

Due to the limitation of hardware, the comparison of large-scale examples cannot be carried out. However, from Table  3 , we can see that the solutions obtained by CIM are all optimal solutions. And the CIM is much faster than the traditional computer in small-scale examples. We can observe that CIM has obvious performance advantages over traditional computers in small-scale examples. In particular, when the scale increases, the time required for CIM does not increase significantly as that of traditional computers. This shows that CIM has great development and application potential. In addition, there is little difference in computing performance between node model and arc model on quantum computer. Node model is slightly faster than arc model, but arc model is more universal than node model. In order to measure the improvement of CIM’s computing efficiency compared with the traditional computer in the given example, we propose the following computation formula.

IMP represents the calculation speed improvement rate, \(Q_{TRA}\) and \(Q_{CIM}\) respectively represent the computation time of traditional computer and CIM on the same example, and both node model and arc model participate in the comparison. After calculating the IMP of all examples, we find that the computation efficiency of CIM is \(92\%\) faster than that of traditional computers.

Conclusion and future research

We applied quantum computing technology to the research on AGV scheduling, and proposed QUBO models that adapts to solve the problem under two different criteria, minimizing total AGV travel time and makespan. Compared with the traditional MIP model, numerical experiments were carried out on traditional computers and CIM. The experimental results proved the superiority and great potential of quantum computing in this field. Of course, due to the limitation of hardware, there are still some shortcomings in this study, which can not show the advantages of quantum computing in large-scale situations. It is believed that with the continuous development of quantum computing technology, the outstanding performance of quantum computing will be demonstrated in solving large-scale problems in the future. In addition, we also summarized the situation that this study can expand, as follows.

First, the model can be improved and expanded. The model we considered above applies to AGVs with a uniform start node and a uniform end node. Realistic scenarios exist where AGVs have different start and end nodes, and our model is easily expandable for these types of cases. The solution is to involve the number of virtual start and end tasks based on the number of AGVs. Due to the difficulty of mapping large-scale optimization problems to the QUBO form with the small number of bits currently available for quantum computing, our proposed model is a pure scheduling problem that does not consider path optimization. Of course, subsequent researchers can consider this possibility in the case of mature technology. We believe that a two-layer planning model can be built on the basis of the existing model, where the scheduling and path planning problems are computationally solved alternately in two sub-models, which reduces both the modeling difficulty and the number of bits used in the solution of a single model.

Second, quantum computer and traditional computer can be combined to study AGV scheduling problem, and their respective characteristics can be better used to improve the efficiency of solving this problem.

Data availability

The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.

Abbreviations

• Automated guided vehicles

Quadratic uncontrained binary optimization

• Coherent Ising machine

Traveling salesman problem

Mixed integer programming

Field programmable gate array

Erbium-doped fiber amplifier

Phase sensitive amplifier

Degenerate optical parametric oscillation

Balanced homodyne detectors

Qin, H. et al. Jd.com: Operations research algorithms drive intelligent warehouse robots to work. INFORMS J. Appl. Anal. 52 , 42–55 (2022).

Article   Google Scholar  

Singh, N., Dang, Q.-V., Akcay, A., Adan, I. & Martagan, T. A matheuristic for AGV scheduling with battery constraints. Eur. J. Oper. Res. 298 , 855–873 (2022).

Article   MathSciNet   Google Scholar  

Zhang, X.-J., Sang, H.-Y., Li, J.-Q., Han, Y.-Y. & Duan, P. An effective multi-AGVs dispatching method applied to matrix manufacturing workshop. Comput. Ind. Eng. 163 , 107791 (2022).

Zhang, L., Yan, Y., Hu, Y. & Ren, W. A dynamic scheduling method for self-organized AGVs in production logistics systems. Procedia CIRP 104 , 381–386 (2021).

Wang, Z. & Zeng, Q. A branch-and-bound approach for AGV dispatching and routing problems in automated container terminals. Comput. Ind. Eng. 166 , 107968 (2022).

Sagar, K. V. & Jerald, J. Real-time automated guided vehicles scheduling with Markov decision process and double q-learning algorithm. Mater. Today Proc. 64 , 279–284 (2022).

Saidi-Mehrabad, M., Dehnavi-Arani, S., Evazabadian, F. & Mahmoodian, V. An ant colony algorithm (aca) for solving the new integrated model of job shop scheduling and conflict-free routing of AGVs. Comput. Ind. Eng. 86 , 2–13 (2015).

Ajagekar, A., Humble, T. & You, F. Quantum computing based hybrid solution strategies for large-scale discrete-continuous optimization problems. Comput. Chem. Eng. 132 , 106630 (2020).

Article   CAS   Google Scholar  

Yamamoto, Y. et al. Coherent ising machines-optical neural networks operating at the quantum limit. NPJ Quant. Inf. 3 , 49 (2017).

Article   ADS   Google Scholar  

Bunyk, P. I. et al. Architectural considerations in the design of a superconducting quantum annealing processor. IEEE Trans. Appl. Supercond. 24 , 1–10 (2014).

Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88 , 063853 (2013).

Marandi, A., Wang, Z., Takata, K., Byer, R. L. & Yamamoto, Y. Network of time-multiplexed optical parametric oscillators as a coherent ising machine. Nat. Photon. 8 , 937–942 (2014).

Article   ADS   CAS   Google Scholar  

McMahon, P. L. et al. A fully programmable 100-spin coherent ising machine with all-to-all connections. Science 354 , 614–617 (2016).

Article   ADS   MathSciNet   CAS   PubMed   Google Scholar  

Inagaki, T. et al. A coherent ising machine for 2000-node optimization problems. Science 354 , 603–606 (2016).

Article   ADS   CAS   PubMed   Google Scholar  

Honjo, T. et al. 100,000-spin coherent ising machine. Sci. Adv. 7 , 0952 (2021).

Lu, B., Fan, C.-R., Liu, L., Wen, K. & Wang, C. Speed-up coherent ising machine with a spiking neural network. Opt. Express 31 , 3676–3684 (2023).

Article   ADS   PubMed   Google Scholar  

Lu, B., Liu, L., Song, J.-Y., Wen, K. & Wang, C. Recent progress on coherent computation based on quantum squeezing. AAPPS Bull. 33 , 7 (2023).

Aonishi, T., Mimura, K., Okada, M. & Yamamoto, Y. L0 regularization-based compressed sensing with quantum-classical hybrid approach. Quant. Sci. Technol. 7 , 035013 (2022).

Takabatake, K., Yanagisawa, K. & Akiyama, Y. Solving generalized polyomino puzzles using the ising model. Entropy 24 , 354 (2022).

Article   ADS   MathSciNet   PubMed   PubMed Central   Google Scholar  

Osaba, E., Villar-Rodriguez, E. & Oregi, I. A systematic literature review of quantum computing for routing problems. IEEE Access (2022).

Goswami, D., Karnick, H., Jain, P. & Maji, H. K. Towards efficiently solving quantum traveling salesman problem. http://arxiv.org/abs/quant-ph/0411013 (2004).

Feld, S. et al. A hybrid solution method for the capacitated vehicle routing problem using a quantum annealer. Front. ICT 6 , 13 (2019).

Bao, S., Tawada, M., Tanaka, S. & Togawa, N. An approach to the vehicle routing problem with balanced pick-up using ising machines. in 2021 International Symposium on VLSI Design, Automation and Test (VLSI-DAT) , 1–4 (IEEE, 2021).

Harwood, S. et al. Formulating and solving routing problems on quantum computers. IEEE Trans. Quant. Eng. 2 , 1–17 (2021).

Geitz, M., Grozea, C., Steigerwald, W., Stöhr, R. & Wolf, A. Solving the extended job shop scheduling problem with AGVs: Classical and quantum approaches. in Integration of Constraint Programming, Artificial Intelligence, and Operations Research , 120–137 (Springer, 2022).

Ohzeki, M., Miki, A., Miyama, M. J. & Terabe, M. Control of automated guided vehicles without collision by quantum annealer and digital devices. Front. Comput. Sci. 1 , 1–10 (2019).

Dang, Q.-V., Singh, N., Adan, I., Martagan, T. & van de Sande, D. Scheduling heterogeneous multi-load AGVs with battery constraints. Comput. Oper. Res. 136 , 105517 (2021).

Hu, Y., Yang, H. & Huang, Y. Conflict-free scheduling of large-scale multi-load AGVs in material transportation network. Transp. Res. E 158 , 102623 (2022).

Murakami, K. Time-space network model and milp formulation of the conflict-free routing problem of a capacitated AGV system. Comput. Ind. Eng. 141 , 106270 (2020).

Ising, E. Contribution to the theory of ferromagnetism. Z. Phys. 31 , 253–258 (1925).

Nabors, C., Yang, S., Day, T. & Byer, R. Coherence properties of a doubly resonant monolithic optical parametric oscillator. JOSA B. 7 , 815–820 (1990).

Marandi, A., Leindecker, N. C., Pervak, V., Byer, R. L. & Vodopyanov, K. L. Coherence properties of a broadband femtosecond mid-ir optical parametric oscillator operating at degeneracy. Opt. Express 20 , 7255–7262 (2012).

Nannicini, G. Performance of hybrid quantum-classical variational heuristics for combinatorial optimization. Phys. Rev. E 99 , 013304 (2019).

Wen, J. et al. Optical experimental solution for the multiway number partitioning problem and its application to computing power scheduling. Sci. Chin. Phys. Mech. Astron. 66 , 290313 (2023).

Rodríguez-Heck, E. Linear and quadratic reformulations of nonlinear optimization problems in binary variables. 4OR 2 , 221–222 (2018).

MathSciNet   Google Scholar  

Chao Yang. Data set. Figshare (2024). Accessed 01 Mar 2024.

Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual (2023).

Huang, Y. et al. Quantum computing for mimo beam selection problem: Model and optical experimental solution. http://arxiv.org/abs/2310.12389 (2023).

Download references

Acknowledgements

The authors would like to thank the team of Bose Quantum Technology Co., Ltd. for helping to obtain experimental data on a quantum computer, the members of this team include Kai Wen, Congyu Cao, Yin Ma and Hai Wei.

This work was partially supported by Grants (72372015, 71871038）from the National Natural Science Foundation of China, Liaoning Provincial Natural Science Foundation (2023-MS-125), and the General support project of China Postdoctoral Science Foundation (2019M661085), and the Humanities and Social Science Foundation of the Ministry of Education(21YJAZH070). Wei Wu was partially supported by JSPS KAKENHI [Grant No.~21K14367] and Industrial Technology Development Organization (NEDO) project (JPNP23003).

Author information

Authors and affiliations.

College of Transportation Engineering, Dalian Maritime University, Dalian, China

Liang Tang & Chao Yang

Beijing QBoson Quantum Technology Co., Ltd, Beijing, China

Faculty of Engineering, Shizuoka University, Hamamatsu, Japan

Department of Information Science and Engineering, Ocean University of China, Qingdao, China

You can also search for this author in PubMed   Google Scholar

Contributions

L.T. has carried out research work division and personnel deployment. C.Y. and W.W are responsible for building the model, and C.Y. is also responsible for the numerical experiment of the classic computer. K.W and his team are responsible for numerical experiments and technical support related to quantum computing. Y.Y.G is responsible for providing guidance on relevant business background. Everyone participated in the writing and revision of the paper. Submission of a paper implies that the work described has not been published previously, that it is not under consideration for publication elsewhere and that its publication is approved by all authors and tacitly or explicitly by the responsible authorities where the work was carried out. Submission also implies that, if accepted, it will not be published elsewhere in the same form, in English or in any other language, without the written consent of the publisher.

Corresponding author

Correspondence to Kai Wen .

Ethics declarations

Competing interests.

The authors declare no competing interests.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary Information

Supplementary information 1., supplementary information 2., supplementary information 3., rights and permissions.

Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/ .

Reprints and permissions

About this article

Cite this article.

Tang, L., Yang, C., Wen, K. et al. Quantum computing for several AGV scheduling models. Sci Rep 14 , 12205 (2024). https://doi.org/10.1038/s41598-024-62821-6

Download citation

Received : 25 November 2023

Accepted : 21 May 2024

Published : 28 May 2024

DOI : https://doi.org/10.1038/s41598-024-62821-6

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Quantum computing
• Quadratic unconstrained binary optimization

By submitting a comment you agree to abide by our Terms and Community Guidelines . If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Quick links

• Explore articles by subject
• Guide to authors
• Editorial policies

Sign up for the Nature Briefing: AI and Robotics newsletter — what matters in AI and robotics research, free to your inbox weekly.

Help | Advanced Search

Mathematics > Numerical Analysis

Title: automatic nonstationary anisotropic tikhonov regularization through bilevel optimization.

Abstract: Regularization techniques are necessary to compute meaningful solutions to discrete ill-posed inverse problems. The well-known 2-norm Tikhonov regularization method equipped with a discretization of the gradient operator as regularization operator penalizes large gradient components of the solution to overcome instabilities. However, this method is homogeneous, i.e., it does not take into account the orientation of the regularized solution and therefore tends to smooth the desired structures, textures and discontinuities, which often contain important information. If the local orientation field of the solution is known, a possible way to overcome this issue is to implement local anisotropic regularization by penalizing weighted directional derivatives. In this paper, considering problems that are inherently two-dimensional, we propose to automatically and simultaneously recover the regularized solution and the local orientation parameters (used to define the anisotropic regularization term) by solving a bilevel optimization problem. Specifically, the lower level problem is Tikhonov regularization equipped with local anisotropic regularization, while the objective function of the upper level problem encodes some natural assumptions about the local orientation parameters and the Tikhonov regularization parameter. Application of the proposed algorithm to a variety of inverse problems in imaging (such as denoising, deblurring, tomography and Dix inversion), with both real and synthetic data, shows its effectiveness and robustness.

Submission history

Access paper:.

• HTML (experimental)
• Other Formats

References & Citations

• Google Scholar
• Semantic Scholar

BibTeX formatted citation

Bibliographic and Citation Tools

Code, data and media associated with this article, recommenders and search tools.

• Institution

arXivLabs: experimental projects with community collaborators

arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.

Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.

Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .

Continuous Exact Relaxation and Alternating Proximal Gradient Algorithm for Partial Sparse and Partial Group Sparse Optimization Problems

• Published: 03 June 2024
• Volume 100 , article number  20 , ( 2024 )

Cite this article

• Qingqing Wu 1 ,
• Dingtao Peng   ORCID: orcid.org/0000-0001-5632-3050 1 &
• Xian Zhang 1  

In this paper, we consider a partial sparse and partial group sparse optimization problem, where the loss function is a continuously differentiable function (possibly nonconvex), and the penalty term consists of two parts associated with sparsity and group sparsity. The first part is the \(\ell _0\) norm of \(\textbf{x}\) , the second part is the \(\ell _{2,0}\) norm of \(\textbf{y}\) , i.e., \(\lambda _1\Vert \textbf{x}\Vert _0+\lambda _2\Vert \textbf{y}\Vert _{2,0}\) , where \((\textbf{x,y})\in \mathbb {R}^{n+m}\) is the decision variable. We give a continuous relaxation model of the above original problem, where the two parts of the penalty term are relaxed by Capped- \(\ell _1\) of \(\textbf{x}\) and group Capped- \(\ell _1\) of \(\textbf{y}\) respectively. Firstly, we define two kinds of first-order stationary points of the relaxation model. Based on the lower bound property of d-stationary points of the relaxation model, we establish the equivalence of solutions of the original problem and the relaxation model, which provides a theoretical basis for solving the original problem via solving the relaxation problem. Secondly, we propose an alternating proximal gradient (APG) algorithm to solve the relaxation model, and prove that the whole sequence of the APG algorithm converges to a critical point under some mild conditions. Finally, numerical experiments on simulated data and multichannel image as well as comparison with some state-of-art algorithms are presented to illustrate the effectiveness and robustness of the proposed algorithm for partial sparse and partial group sparse optimization problem.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Price includes VAT (Russian Federation)

Instant access to the full article PDF.

Rent this article via DeepDyve

Institutional subscriptions

Data Availability

All data included in this manuscript are available upon reasonable request by contact with the corresponding author.

Attouch, H., Bolte, J.: On the convergence of the proximal algorithm for nonsmooth functions involving analytic features. Math. Program. 116 (1–2), 5–16 (2009)

Article   MathSciNet   Google Scholar  

Attouch, H., Bolte, J., Redont, P., Soubeyran, A.: Proximal alternating minimization and projection methods for nonconvex problems: an approach based on the Kurdyka-Łojasiewicz inequality. Math. Oper. Res. 35 (2), 438–457 (2010)

Bian, W., Chen, X.: A smoothing proximal gradient algorithm for nonsmooth convex regression with cardinality penalty. SIAM J. Numer. Anal. 58 (1), 858–883 (2020)

Bian, W., Chen, X.: Optimality and complexity for constrained optimization problems with nonconvex regularization. Math. Oper. Res. 42 (4), 1063–1084 (2017)

Blumensath, T.: Compressed sensing with nonlinear observations and related nonlinear optimization problems. IEEE Trans. Inf. Theory 59 (6), 3466–3474 (2013)

Bolte, J., Daniilidis, A., Lewis, A.: The Łojasiewicz inequality for nonsmooth subanalytic functions with applications to subgradient dynamical systems. SIAM J. Optim. 17 (4), 1205–1223 (2007)

Article   Google Scholar  

Bolte, J., Sabach, S., Teboulle, M.: Proximal alternating linearized minimization for nonconvex and nonsmooth problems. Math. Program. 146 (1–2), 459–494 (2014)

Breheny, P., Huang, J.: Group descent algorithms for nonconvex penalized linear and logistic regression models with grouped predictors. Stat. Comput. 25 (2), 173–187 (2015)

Chandran, M.: Analysis of Bayesian Group-Lasso in Regression Models. University of Florida, Gainesville (2011)

Google Scholar  

Chartrand, R.: Exact reconstruction of sparse signals via nonconvex minimization. IEEE Signal Process. Lett. 14 (10), 707–710 (2007)

Chen, X., Pan, L., Xiu, N.: Solution sets of three sparse optimization problems for multivariate regression. J. Global Optim. 87 (2–4), 347–371 (2023)

Chen, X., Xu, F., Ye, Y.: Lower bound theory of nonzero entries in solutions of \(\ell _2\) - \(\ell _p\) minimization. SIAM J. Sci. Comput. 32 (5), 2832–2852 (2010)

Clarke, F.H.: Optimization and nonsmooth analysis. SIAM J. Control Optim. (1990)

Elad, M., Figueiredo, M.A.T., Ma, Y.: On the role of sparse and redundant representations in image processing. Proc. IEEE 98 (6), 972–982 (2010)

Fan, J., Li, R.: Statistical challenges with high dimensionality: feature selection in knowledge discovery. Proc. Int. Congr. Math. 3 , 595–622 (2006)

MathSciNet   Google Scholar  

Fan, J., Li, R.: Variable selection via nonconvave penalized likelihood and its oracle properties. J. Am. Stat. Assoc. 96 (456), 1348–1360 (2001)

Feng, X., Yan, S., Wu, C.: The \(\ell _{2, q}\) regularized group sparse optimization: lower bound theory, recovery bound and algorithms. Appl. Comput. Harmon. Anal. 49 (2), 381–414 (2020)

Gong, P., Zhang, C., Lu, Z., Huang, J., Ye, J.: A general iterative shrinkage and thresholding algorithm for non-convex regularized optimization problems. In: Proceedings of the 30th International Conference on International Conference on Machine Learning (ICML’13), vol. 28(2), pp. 37–45 (2013)

Huang, J., Ma, S., Xie, H., Zhang, C.H.: A group bridge approach for variable selection. Biometrika 96 (2), 339–355 (2009)

Huang, J., Zhang, T.: The benefit of group sparsity. Ann. Stat. 38 (4), 1978–2004 (2010)

Hu, Y., Li, C., Meng, K., Qin, J., Yang, X.: Group sparse optimization via \(\ell _{p, q}\) regularization. J. Mach. Learn. Res. 18 (30), 1–52 (2017)

Jiang, D.: Concave Selection in Generalized Linear Models. University of Iowa, Iowa City (2012)

Book   Google Scholar  

Jiao, Y., Jin, B., Lu, X.: Group sparse recovery via the \(\ell _{0}(\ell _2)\) penalty: theory and algorithm. IEEE Trans. Signal Process. 65 (4), 998–1012 (2017)

Le Thi, H.A., Pham Dinh, T., Le, H.M., Vo, X.T.: DC approximation approaches for sparse optimization. Eur. J. Oper. Res. 244 (1), 26–46 (2015)

Li, W., Bian, W., Toh, K.C.: DC algorithms for a class of sparse group \(\ell _0 \) regularized optimization problems. SIAM J. Optim. 32 (3), 1614–1641 (2022)

Nikolova, M., Tan, P.: Alternating structure-adapted proximal gradient descent for nonconvex nonsmooth block-regularized problems. SIAM J. Optim. 29 (3), 2053–2078 (2019)

Ong, C.S., An, L.T.H.: Learning sparse classifiers with difference of convex functions algorithms. Optim. Methods Softw. 28 (4), 830–854 (2013)

Pang, J.S., Razaviyayn, M., Alvarado, A.: Computing B-stationary points of nonsmooth DC programs. Math. Oper. Res. 42 (1), 95–118 (2017)

Pan, L., Chen, X.: Group sparse optimization for images recovery using capped folded concave functions. SIAM J. Imag. Sci. 14 (1), 1–25 (2021)

Peng, D., Chen, X.: Computation of second-order directional stationary points for group sparse optimization. Optim. Methods Softw. 35 (2), 348–376 (2020)

Phan, D.N., Le Thi, H.A.: Group variable selection via \(\ell _{p,0}\) regularization and application to optimal scoring. Neural Netw. 118 , 220–234 (2019)

Raman, S., Fuchs, T.J., Wild, P.J.: The Bayesian group-Lasso for analyzing contingency tables. In: Proceedings of the 26th Annual International Conference on Machine Learning, pp. 881–888 (2009)

Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (2009)

Shen, H., Peng, D., Zhang, X.: Smoothing composite proximal gradient algorithm for sparse group Lasso problems with nonsmooth loss functions. J. Appl. Math. Comput. (2024). https://doi.org/10.1007/s12190-024-02034-2

Simon, N., Friedman, J., Hastie, T., Tibshirani, R.: A sparse-group Lasso. J. Comput. Graph. Stat. 22 (2), 231–245 (2013)

Soubies, E., Blanc-Féraud, L., Aubert, G.: A continuous exact \(\ell _0\) penalty (Capped- \(\ell _0\) ) for least squares regularized problem. SIAM J. Imaging Sci. 8 (3), 1574–1606 (2015)

Soubies, E., Blanc-Féraud, L., Aubert, G.: A unified view of exact continuous penalties for \(\ell _2-\ell _0\) minimization. SIAM J. Optim. 27 (3), 2034–2060 (2017)

Van den Berg, E., Friedlander, M.P.: Probing the pareto frontier for basis pursuit solutions. SIAM J. Sci. Comput. 31 (2), 890–912 (2009)

Wang, L., Chen, G., Li, H.: Group SCAD regression analysis for microarray time course gene expression data. Bioinformatics 23 (12), 1486–1494 (2007)

Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. Ser. B (Stat. Methodol.) 68 (1), 49–67 (2006)

Zhang, C.H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38 (2), 894–942 (2010)

Zhang, T.: Analysis of multi-stage convex relaxation for sparse regularization. J. Mach. Learn. Res. 11 (35), 1081–1107 (2010)

Zhang, X., Peng, D.: Solving constrained nonsmooth group sparse optimization via group Capped- \(\ell _1\) relaxation and group smoothing proximal gradient algorithm. Comput. Optim. Appl. 83 (3), 801–844 (2022)

Zhang, X., Peng, D., Su, Y.: A singular value shrinkage thresholding algorithm for folded concave penalized low-rank matrix optimization problems. J. Global Optim. 88 (2), 485–508 (2024)

Zhang, Y., Zhang, N., Sun, D.: An efficient Hessian based algorithm for solving large-scale sparse group Lasso problems. Math. Program. 179 (1), 223–263 (2020)

Zhao, P., Rocha, G., Yu, B.: The composite absolute penalties family for grouped and hierarchical variable selection. Ann. Stat. 37 (6A), 3468–3497 (2009)

Zhou, Y., Han, J., Yuan, X.: Inverse sparse group Lasso model for robust object tracking. IEEE Trans. Multimed. 19 (8), 1798–1810 (2017)

Download references

Acknowledgements

This work is supported by the National Natural Science Foundation of China (12261020), the Guizhou Provincial Science and Technology Program (ZK[2021]009), the Foundation for Selected Excellent Project of Guizhou Province for High-level Talents Back from Overseas ([2018]03), and the Research Foundation for Postgraduates of Guizhou Province (YJSCXJH[2020]085).

Author information

Authors and affiliations.

School of Mathematics and Statistics, Guizhou University, Guiyang, 550025, China

Qingqing Wu, Dingtao Peng & Xian Zhang

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Dingtao Peng .

Ethics declarations

Conflict of interest.

The authors declare no conflict of interest.

Additional information

Publisher's note.

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Wu, Q., Peng, D. & Zhang, X. Continuous Exact Relaxation and Alternating Proximal Gradient Algorithm for Partial Sparse and Partial Group Sparse Optimization Problems. J Sci Comput 100 , 20 (2024). https://doi.org/10.1007/s10915-024-02584-4

Download citation

Received : 30 September 2023

Revised : 13 April 2024

Accepted : 24 May 2024

Published : 03 June 2024

DOI : https://doi.org/10.1007/s10915-024-02584-4

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• Partial sparse and partial group sparse optimization problem
• Continuous exact relaxation
• Stationary point
• Alternating proximal gradient algorithm
• The whole sequence convergence

Mathematics Subject Classification

• Find a journal
• Publish with us
• Track your research