solution no problem

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.4: Existence and Uniqueness of Solutions

• Last updated
• Save as PDF
• Page ID 63380

• Gregory Hartman et al.
• Virginia Military Institute

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• T/F: It is possible for a linear system to have exactly 5 solutions.
• T/F: A variable that corresponds to a leading 1 is “free.”
• How can one tell what kind of solution a linear system of equations has?
• Give an example (different from those given in the text) of a 2 equation, 2 unknown linear system that is not consistent.
• T/F: A particular solution for a linear system with infinite solutions can be found by arbitrarily picking values for the free variables.

So far, whenever we have solved a system of linear equations, we have always found exactly one solution. This is not always the case; we will find in this section that some systems do not have a solution, and others have more than one.

We start with a very simple example. Consider the following linear system: \[x-y=0. \nonumber \] There are obviously infinite solutions to this system; as long as \(x=y\) , we have a solution. We can picture all of these solutions by thinking of the graph of the equation \(y=x\) on the traditional \(x,y\) coordinate plane.

Let’s continue this visual aspect of considering solutions to linear systems. Consider the system \[\begin{align}\begin{aligned} x+y&=2\\ x-y&=0. \end{aligned}\end{align} \nonumber \] Each of these equations can be viewed as lines in the coordinate plane, and since their slopes are different, we know they will intersect somewhere (see Figure \(\PageIndex{1}\)(a)). In this example, they intersect at the point \((1,1)\) – that is, when \(x=1\) and \(y=1\) , both equations are satisfied and we have a solution to our linear system. Since this is the only place the two lines intersect, this is the only solution.

Now consider the linear system \[\begin{align}\begin{aligned} x+y&=1\\2x+2y&=2.\end{aligned}\end{align} \nonumber \] It is clear that while we have two equations, they are essentially the same equation; the second is just a multiple of the first. Therefore, when we graph the two equations, we are graphing the same line twice (see Figure \(\PageIndex{1}\)(b); the thicker line is used to represent drawing the line twice). In this case, we have an infinite solution set, just as if we only had the one equation \(x+y=1\) . We often write the solution as \(x=1-y\) to demonstrate that \(y\) can be any real number, and \(x\) is determined once we pick a value for \(y\) .

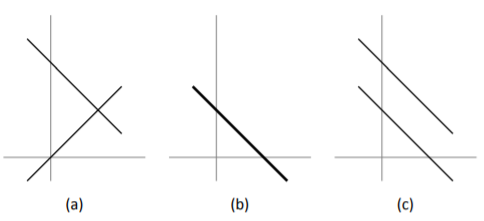
Figure \(\PageIndex{1}\): The three possibilities for two linear equations with two unknowns.

Finally, consider the linear system \[\begin{align}\begin{aligned} x+y&=1\\x+y&=2.\end{aligned}\end{align} \nonumber \] We should immediately spot a problem with this system; if the sum of \(x\) and \(y\) is 1, how can it also be 2? There is no solution to such a problem; this linear system has no solution. We can visualize this situation in Figure \(\PageIndex{1}\) (c); the two lines are parallel and never intersect.

If we were to consider a linear system with three equations and two unknowns, we could visualize the solution by graphing the corresponding three lines. We can picture that perhaps all three lines would meet at one point, giving exactly 1 solution; perhaps all three equations describe the same line, giving an infinite number of solutions; perhaps we have different lines, but they do not all meet at the same point, giving no solution. We further visualize similar situations with, say, 20 equations with two variables.

While it becomes harder to visualize when we add variables, no matter how many equations and variables we have, solutions to linear equations always come in one of three forms: exactly one solution, infinite solutions, or no solution. This is a fact that we will not prove here, but it deserves to be stated.

Theorem \(\PageIndex{1}\)

Solution Forms of Linear Systems

Every linear system of equations has exactly one solution, infinite solutions, or no solution.

This leads us to a definition. Here we don’t differentiate between having one solution and infinite solutions, but rather just whether or not a solution exists.

Definition: Consistent and Inconsistent Linear Systems

A system of linear equations is consistent if it has a solution (perhaps more than one). A linear system is inconsistent if it does not have a solution.

How can we tell what kind of solution (if one exists) a given system of linear equations has? The answer to this question lies with properly understanding the reduced row echelon form of a matrix. To discover what the solution is to a linear system, we first put the matrix into reduced row echelon form and then interpret that form properly.

Before we start with a simple example, let us make a note about finding the reduced row echelon form of a matrix.

In the previous section, we learned how to find the reduced row echelon form of a matrix using Gaussian elimination – by hand. We need to know how to do this; understanding the process has benefits. However, actually executing the process by hand for every problem is not usually beneficial. In fact, with large systems, computing the reduced row echelon form by hand is effectively impossible. Our main concern is what “the rref” is, not what exact steps were used to arrive there. Therefore, the reader is encouraged to employ some form of technology to find the reduced row echelon form. Computer programs such as Mathematica , MATLAB, Maple, and Derive can be used; many handheld calculators (such as Texas Instruments calculators) will perform these calculations very quickly.

As a general rule, when we are learning a new technique, it is best to not use technology to aid us. This helps us learn not only the technique but some of its “inner workings.” We can then use technology once we have mastered the technique and are now learning how to use it to solve problems.

From here on out, in our examples, when we need the reduced row echelon form of a matrix, we will not show the steps involved. Rather, we will give the initial matrix, then immediately give the reduced row echelon form of the matrix. We trust that the reader can verify the accuracy of this form by both performing the necessary steps by hand or utilizing some technology to do it for them.

Our first example explores officially a quick example used in the introduction of this section.

Example \(\PageIndex{1}\)

Find the solution to the linear system

\[\begin{array}{ccccc} x_1 & +& x_2 & = & 1\\ 2x_1 & + & 2x_2 & = &2\end{array} . \nonumber \]

Create the corresponding augmented matrix, and then put the matrix into reduced row echelon form.

\[\left[\begin{array}{ccc}{1}&{1}&{1}\\{2}&{2}&{2}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{ccc}{1}&{1}&{1}\\{0}&{0}&{0}\end{array}\right] \nonumber \]

Now convert the reduced matrix back into equations. In this case, we only have one equation, \[x_1+x_2=1 \nonumber \] or, equivalently, \[\begin{align}\begin{aligned} x_1 &=1-x_2\\ x_2&\text{ is free}. \end{aligned}\end{align} \nonumber \]

We have just introduced a new term, the word free . It is used to stress that idea that \(x_2\) can take on any value; we are “free” to choose any value for \(x_2\) . Once this value is chosen, the value of \(x_1\) is determined. We have infinite choices for the value of \(x_2\) , so therefore we have infinite solutions.

For example, if we set \(x_2 = 0\) , then \(x_1 = 1\) ; if we set \(x_2 = 5\) , then \(x_1 = -4\) .

Let’s try another example, one that uses more variables.

Example \(\PageIndex{2}\)

Find the solution to the linear system \[\begin{array}{ccccccc} & &x_2&-&x_3&=&3\\ x_1& & &+&2x_3&=&2\\ &&-3x_2&+&3x_3&=&-9\\ \end{array}. \nonumber \]

To find the solution, put the corresponding matrix into reduced row echelon form.

\[\left[\begin{array}{cccc}{0}&{1}&{-1}&{3}\\{1}&{0}&{2}&{2}\\{0}&{-3}&{3}&{-9}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{2}&{2}\\{0}&{1}&{-1}&{3}\\{0}&{0}&{0}&{0}\end{array}\right] \nonumber \]

Now convert this reduced matrix back into equations. We have \[\begin{align}\begin{aligned} x_1 + 2x_3 &= 2 \\ x_2-x_3&=3 \end{aligned}\end{align} \nonumber \] or, equivalently, \[\begin{align}\begin{aligned} x_1 &= 2-2x_3 \\ x_2&=3+x_3\\x_3&\text{ is free.} \end{aligned}\end{align} \nonumber \]

These two equations tell us that the values of \(x_1\) and \(x_2\) depend on what \(x_3\) is. As we saw before, there is no restriction on what \(x_3\) must be; it is “free” to take on the value of any real number. Once \(x_3\) is chosen, we have a solution. Since we have infinite choices for the value of \(x_3\) , we have infinite solutions.

As examples, \(x_1 = 2\) , \(x_2 = 3\) , \(x_3 = 0\) is one solution; \(x_1 = -2\) , \(x_2 = 5\) , \(x_3 = 2\) is another solution. Try plugging these values back into the original equations to verify that these indeed are solutions. (By the way, since infinite solutions exist, this system of equations is consistent.)

In the two previous examples we have used the word “free” to describe certain variables. What exactly is a free variable? How do we recognize which variables are free and which are not?

Look back to the reduced matrix in Example \(\PageIndex{1}\). Notice that there is only one leading 1 in that matrix, and that leading 1 corresponded to the \(x_1\) variable. That told us that \(x_1\) was not a free variable; since \(x_2\) did not correspond to a leading 1, it was a free variable.

Look also at the reduced matrix in Example \(\PageIndex{2}\). There were two leading 1s in that matrix; one corresponded to \(x_1\) and the other to \(x_2\) . This meant that \(x_1\) and \(x_2\) were not free variables; since there was not a leading 1 that corresponded to \(x_3\) , it was a free variable.

We formally define this and a few other terms in this following definition.

Definition: Dependent and Independent Variables

Consider the reduced row echelon form of an augmented matrix of a linear system of equations. Then:

a variable that corresponds to a leading 1 is a basic , or dependent , variable, and

a variable that does not correspond to a leading 1 is a free , or independent , variable.

One can probably see that “free” and “independent” are relatively synonymous. It follows that if a variable is not independent, it must be dependent; the word “basic” comes from connections to other areas of mathematics that we won’t explore here.

These definitions help us understand when a consistent system of linear equations will have infinite solutions. If there are no free variables, then there is exactly one solution; if there are any free variables, there are infinite solutions.

Key Idea \(\PageIndex{1}\): Consistent Solution Types

A consistent linear system of equations will have exactly one solution if and only if there is a leading 1 for each variable in the system.

If a consistent linear system of equations has a free variable, it has infinite solutions.

If a consistent linear system has more variables than leading 1s, then the system will have infinite solutions.

A consistent linear system with more variables than equations will always have infinite solutions.

Key Idea \(\PageIndex{1}\) applies only to consistent systems. If a system is inconsistent , then no solution exists and talking about free and basic variables is meaningless.

When a consistent system has only one solution, each equation that comes from the reduced row echelon form of the corresponding augmented matrix will contain exactly one variable. If the consistent system has infinite solutions, then there will be at least one equation coming from the reduced row echelon form that contains more than one variable. The “first” variable will be the basic (or dependent) variable; all others will be free variables.

We have now seen examples of consistent systems with exactly one solution and others with infinite solutions. How will we recognize that a system is inconsistent? Let’s find out through an example.

Example \(\PageIndex{3}\)

Find the solution to the linear system \[\begin{array}{ccccccc} x_1&+&x_2&+&x_3&=&1\\ x_1&+&2x_2&+&x_3&=&2\\ 2x_1&+&3x_2&+&2x_3&=&0\\ \end{array}. \nonumber \]

We start by putting the corresponding matrix into reduced row echelon form.

\[\left[\begin{array}{cccc}{1}&{1}&{1}&{1}\\{1}&{2}&{1}&{2}\\{2}&{3}&{2}&{0}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{1}&{0}\\{0}&{1}&{0}&{0}\\{0}&{0}&{0}&{1}\end{array}\right] \nonumber \]

Now let us take the reduced matrix and write out the corresponding equations. The first two rows give us the equations \[\begin{align}\begin{aligned} x_1+x_3&=0\\ x_2 &= 0.\\ \end{aligned}\end{align} \nonumber \] So far, so good. However the last row gives us the equation \[0x_1+0x_2+0x_3 = 1 \nonumber \] or, more concisely, \(0=1\) . Obviously, this is not true; we have reached a contradiction. Therefore, no solution exists; this system is inconsistent.

In previous sections we have only encountered linear systems with unique solutions (exactly one solution). Now we have seen three more examples with different solution types. The first two examples in this section had infinite solutions, and the third had no solution. How can we tell if a system is inconsistent?

A linear system will be inconsistent only when it implies that 0 equals 1. We can tell if a linear system implies this by putting its corresponding augmented matrix into reduced row echelon form. If we have any row where all entries are 0 except for the entry in the last column, then the system implies 0=1. More succinctly, if we have a leading 1 in the last column of an augmented matrix, then the linear system has no solution.

Key Idea \(\PageIndex{2}\): Inconsistent Systems of Linear Equations

A system of linear equations is inconsistent if the reduced row echelon form of its corresponding augmented matrix has a leading 1 in the last column.

Example \(\PageIndex{4}\)

Confirm that the linear system \[\begin{array}{ccccc} x&+&y&=&0 \\2x&+&2y&=&4 \end{array} \nonumber \] has no solution.

We can verify that this system has no solution in two ways. First, let’s just think about it. If \(x+y=0\) , then it stands to reason, by multiplying both sides of this equation by 2, that \(2x+2y = 0\) . However, the second equation of our system says that \(2x+2y= 4\) . Since \(0\neq 4\) , we have a contradiction and hence our system has no solution. (We cannot possibly pick values for \(x\) and \(y\) so that \(2x+2y\) equals both 0 and 4.)

Now let us confirm this using the prescribed technique from above. The reduced row echelon form of the corresponding augmented matrix is

\[\left[\begin{array}{ccc}{1}&{1}&{0}\\{0}&{0}&{1}\end{array}\right] \nonumber \]

We have a leading 1 in the last column, so therefore the system is inconsistent.

Let’s summarize what we have learned up to this point. Consider the reduced row echelon form of the augmented matrix of a system of linear equations. \(^{1}\) If there is a leading 1 in the last column, the system has no solution. Otherwise, if there is a leading 1 for each variable, then there is exactly one solution; otherwise (i.e., there are free variables) there are infinite solutions.

Systems with exactly one solution or no solution are the easiest to deal with; systems with infinite solutions are a bit harder to deal with. Therefore, we’ll do a little more practice. First, a definition: if there are infinite solutions, what do we call one of those infinite solutions?

Definition: Particular Solution

Consider a linear system of equations with infinite solutions. A particular solution is one solution out of the infinite set of possible solutions.

The easiest way to find a particular solution is to pick values for the free variables which then determines the values of the dependent variables. Again, more practice is called for.

Example \(\PageIndex{5}\)

Give the solution to a linear system whose augmented matrix in reduced row echelon form is

\[\left[\begin{array}{ccccc}{1}&{-1}&{0}&{2}&{4}\\{0}&{0}&{1}&{-3}&{7}\\{0}&{0}&{0}&{0}&{0}\end{array}\right] \nonumber \]

and give two particular solutions.

We can essentially ignore the third row; it does not divulge any information about the solution. \(^{2}\) The first and second rows can be rewritten as the following equations: \[\begin{align}\begin{aligned} x_1 - x_2 + 2x_4 &=4 \\ x_3 - 3x_4 &= 7. \\ \end{aligned}\end{align} \nonumber \] Notice how the variables \(x_1\) and \(x_3\) correspond to the leading 1s of the given matrix. Therefore \(x_1\) and \(x_3\) are dependent variables; all other variables (in this case, \(x_2\) and \(x_4\) ) are free variables.

We generally write our solution with the dependent variables on the left and independent variables and constants on the right. It is also a good practice to acknowledge the fact that our free variables are, in fact, free. So our final solution would look something like \[\begin{align}\begin{aligned} x_1 &= 4 +x_2 - 2x_4 \\ x_2 & \text{ is free} \\ x_3 &= 7+3x_4 \\ x_4 & \text{ is free}.\end{aligned}\end{align} \nonumber \]

To find particular solutions, choose values for our free variables. There is no “right” way of doing this; we are “free” to choose whatever we wish.

By setting \(x_2 = 0 = x_4\) , we have the solution \(x_1 = 4\) , \(x_2 = 0\) , \(x_3 = 7\) , \(x_4 = 0\) . By setting \(x_2 = 1\) and \(x_4 = -5\) , we have the solution \(x_1 = 15\) , \(x_2 = 1\) , \(x_3 = -8\) , \(x_4 = -5\) . It is easier to read this when are variables are listed vertically, so we repeat these solutions:

One particular solution is:

\[\begin{align}\begin{aligned} x_1 &= 4\\ x_2 &=0 \\ x_3 &= 7 \\ x_4 &= 0. \end{aligned}\end{align} \nonumber \]

Another particular solution is:

\[\begin{align}\begin{aligned} x_1 &= 15\\ x_2 &=1 \\ x_3 &= -8 \\ x_4 &= -5. \end{aligned}\end{align} \nonumber \]

Example \(\PageIndex{6}\)

Find the solution to a linear system whose augmented matrix in reduced row echelon form is

\[\left[\begin{array}{ccccc}{1}&{0}&{0}&{2}&{3}\\{0}&{1}&{0}&{4}&{5}\end{array}\right] \nonumber \]

Converting the two rows into equations we have \[\begin{align}\begin{aligned} x_1 + 2x_4 &= 3 \\ x_2 + 4x_4&=5.\\ \end{aligned}\end{align} \nonumber \]

We see that \(x_1\) and \(x_2\) are our dependent variables, for they correspond to the leading 1s. Therefore, \(x_3\) and \(x_4\) are independent variables. This situation feels a little unusual, \(^{3}\) for \(x_3\) doesn’t appear in any of the equations above, but cannot overlook it; it is still a free variable since there is not a leading 1 that corresponds to it. We write our solution as: \[\begin{align}\begin{aligned} x_1 &= 3-2x_4 \\ x_2 &=5-4x_4 \\ x_3 & \text{ is free} \\ x_4 & \text{ is free}. \\ \end{aligned}\end{align} \nonumber \]

To find two particular solutions, we pick values for our free variables. Again, there is no “right” way of doing this (in fact, there are \(\ldots\) infinite ways of doing this) so we give only an example here.

\[\begin{align}\begin{aligned} x_1 &= 3\\ x_2 &=5 \\ x_3 &= 1000 \\ x_4 &= 0. \end{aligned}\end{align} \nonumber \]

\[\begin{align}\begin{aligned} x_1 &= 3-2\pi\\ x_2 &=5-4\pi \\ x_3 &= e^2 \\ x_4 &= \pi. \end{aligned}\end{align} \nonumber \]

(In the second particular solution we picked “unusual” values for \(x_3\) and \(x_4\) just to highlight the fact that we can.)

Example \(\PageIndex{7}\)

Find the solution to the linear system \[\begin{array}{ccccccc}x_1&+&x_2&+&x_3&=&5\\x_1&-&x_2&+&x_3&=&3\\ \end{array} \nonumber \] and give two particular solutions.

The corresponding augmented matrix and its reduced row echelon form are given below.

\[\left[\begin{array}{cccc}{1}&{1}&{1}&{5}\\{1}&{-1}&{1}&{3}\end{array}\right]\qquad\overrightarrow{\text{rref}}\qquad\left[\begin{array}{cccc}{1}&{0}&{1}&{4}\\{0}&{1}&{0}&{1}\end{array}\right] \nonumber \]

Converting these two rows into equations, we have \[\begin{align}\begin{aligned} x_1+x_3&=4\\x_2&=1\\ \end{aligned}\end{align} \nonumber \] giving us the solution \[\begin{align}\begin{aligned} x_1&= 4-x_3\\x_2&=1\\x_3 &\text{ is free}.\\ \end{aligned}\end{align} \nonumber \]

Once again, we get a bit of an “unusual” solution; while \(x_2\) is a dependent variable, it does not depend on any free variable; instead, it is always 1. (We can think of it as depending on the value of 1.) By picking two values for \(x_3\) , we get two particular solutions.

\[\begin{align}\begin{aligned} x_1 &= 4\\ x_2 &=1 \\ x_3 &= 0 . \end{aligned}\end{align} \nonumber \]

\[\begin{align}\begin{aligned} x_1 &= 3\\ x_2 &=1 \\ x_3 &= 1 . \end{aligned}\end{align} \nonumber \]

The constants and coefficients of a matrix work together to determine whether a given system of linear equations has one, infinite, or no solution. The concept will be fleshed out more in later chapters, but in short, the coefficients determine whether a matrix will have exactly one solution or not. In the “or not” case, the constants determine whether or not infinite solutions or no solution exists. (So if a given linear system has exactly one solution, it will always have exactly one solution even if the constants are changed.) Let’s look at an example to get an idea of how the values of constants and coefficients work together to determine the solution type.

Example \(\PageIndex{8}\)

For what values of \(k\) will the given system have exactly one solution, infinite solutions, or no solution? \[\begin{array}{ccccc}x_1&+&2x_2&=&3\\ 3x_1&+&kx_2&=&9\end{array} \nonumber \]

We answer this question by forming the augmented matrix and starting the process of putting it into reduced row echelon form. Below we see the augmented matrix and one elementary row operation that starts the Gaussian elimination process.

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{3}&{k}&{9}\end{array}\right]\qquad\overrightarrow{-3R_{1}+R_{2}\to R_{2}}\qquad\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{k-6}&{0}\end{array}\right] \nonumber \]

This is as far as we need to go. In looking at the second row, we see that if \(k=6\) , then that row contains only zeros and \(x_2\) is a free variable; we have infinite solutions. If \(k\neq 6\) , then our next step would be to make that second row, second column entry a leading one. We don’t particularly care about the solution, only that we would have exactly one as both \(x_1\) and \(x_2\) would correspond to a leading one and hence be dependent variables.

Our final analysis is then this. If \(k\neq 6\) , there is exactly one solution; if \(k=6\) , there are infinite solutions. In this example, it is not possible to have no solutions.

As an extension of the previous example, consider the similar augmented matrix where the constant 9 is replaced with a 10. Performing the same elementary row operation gives

\[\left[\begin{array}{ccc}{1}&{2}&{3}\\{3}&{k}&{10}\end{array}\right]\qquad\overrightarrow{-3R_{1}+R_{2}\to R_{2}}\qquad\left[\begin{array}{ccc}{1}&{2}&{3}\\{0}&{k-6}&{1}\end{array}\right] \nonumber \]

As in the previous example, if \(k\neq6\) , we can make the second row, second column entry a leading one and hence we have one solution. However, if \(k=6\) , then our last row is \([0\ 0\ 1]\) , meaning we have no solution.

We have been studying the solutions to linear systems mostly in an “academic” setting; we have been solving systems for the sake of solving systems. In the next section, we’ll look at situations which create linear systems that need solving (i.e., “word problems”).

[1] That sure seems like a mouthful in and of itself. However, it boils down to “look at the reduced form of the usual matrix.”

[2] Then why include it? Rows of zeros sometimes appear “unexpectedly” in matrices after they have been put in reduced row echelon form. When this happens, we do learn something ; it means that at least one equation was a combination of some of the others.

[3] What kind of situation would lead to a column of all zeros? To have such a column, the original matrix needed to have a column of all zeros, meaning that while we acknowledged the existence of a certain variable, we never actually used it in any equation. In practical terms, we could respond by removing the corresponding column from the matrix and just keep in mind that that variable is free. In very large systems, it might be hard to determine whether or not a variable is actually used and one would not worry about it.

When we learn about s and s, we will see that under certain circumstances this situation arises. In those cases we leave the variable in the system just to remind ourselves that it is there.

No Solution Equation

Solving Equations

What is an equation.

An equation says that two things are equal. It will have an equals sign "=" like this:

That equations says:

what is on the left (x − 2)  equals  what is on the right (4)

So an equation is like a statement " this equals that "

What is a Solution?

A Solution is a value we can put in place of a variable (such as x ) that makes the equation true .

Example: x − 2 = 4

When we put 6 in place of x we get:

which is true

So x = 6 is a solution.

How about other values for x ?

• For x=5 we get "5−2=4" which is not true , so x=5 is not a solution .
• For x=9 we get "9−2=4" which is not true , so x=9 is not a solution .

In this case x = 6 is the only solution.

You might like to practice solving some animated equations .

More Than One Solution

There can be more than one solution.

Example: (x−3)(x−2) = 0

When x is 3 we get:

(3−3)(3−2) = 0 × 1 = 0

And when x is 2 we get:

(2−3)(2−2) = (−1) × 0 = 0

which is also true

So the solutions are:

x = 3 , or x = 2

When we gather all solutions together it is called a Solution Set

The above solution set is: {2, 3}

Solutions Everywhere!

Some equations are true for all allowed values and are then called Identities

Example: sin(−θ) = −sin(θ) is one of the Trigonometric Identities

Let's try θ = 30°:

sin(−30°) = −0.5 and

−sin(30°) = −0.5

So it is true for θ = 30°

Let's try θ = 90°:

sin(−90°) = −1 and

−sin(90°) = −1

So it is also true for θ = 90°

Is it true for all values of θ ? Try some values for yourself!

How to Solve an Equation

There is no "one perfect way" to solve all equations.

A Useful Goal

But we often get success when our goal is to end up with:

x = something

In other words, we want to move everything except "x" (or whatever name the variable has) over to the right hand side.

Example: Solve 3x−6 = 9

Now we have x = something ,

and a short calculation reveals that x = 5

Like a Puzzle

In fact, solving an equation is just like solving a puzzle. And like puzzles, there are things we can (and cannot) do.

Here are some things we can do:

• Add or Subtract the same value from both sides
• Clear out any fractions by Multiplying every term by the bottom parts
• Divide every term by the same nonzero value
• Combine Like Terms
• Expanding (the opposite of factoring) may also help
• Recognizing a pattern, such as the difference of squares
• Sometimes we can apply a function to both sides (e.g. square both sides)

Example: Solve √(x/2) = 3

And the more "tricks" and techniques you learn the better you will get.

Special Equations

There are special ways of solving some types of equations. Learn how to ...

• solve Quadratic Equations
• solve Radical Equations
• solve Equations with Sine, Cosine and Tangent

Check Your Solutions

You should always check that your "solution" really is a solution.

How To Check

Take the solution(s) and put them in the original equation to see if they really work.

Example: solve for x:

2x x − 3 + 3 = 6 x − 3     (x≠3)

We have said x≠3 to avoid a division by zero.

Let's multiply through by (x − 3) :

2x + 3(x−3) = 6

Bring the 6 to the left:

2x + 3(x−3) − 6 = 0

Expand and solve:

2x + 3x − 9 − 6 = 0

5x − 15 = 0

5(x − 3) = 0

Which can be solved by having x=3

Let us check x=3 using the original question:

2 × 3 3 − 3 + 3  =   6 3 − 3

Hang On: 3 − 3 = 0 That means dividing by Zero!

And anyway, we said at the top that x≠3 , so ...

x = 3 does not actually work, and so:

There is No Solution!

That was interesting ... we thought we had found a solution, but when we looked back at the question we found it wasn't allowed!

This gives us a moral lesson:

"Solving" only gives us possible solutions, they need to be checked!

• Note down where an expression is not defined (due to a division by zero, the square root of a negative number, or some other reason)
• Show all the steps , so it can be checked later (by you or someone else)

Equation Solver

Enter the Equation you want to solve into the editor.

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

HIGH SCHOOL

• ACT Tutoring
• SAT Tutoring
• PSAT Tutoring
• ASPIRE Tutoring
• SHSAT Tutoring
• STAAR Tutoring

GRADUATE SCHOOL

• MCAT Tutoring
• GRE Tutoring
• LSAT Tutoring
• GMAT Tutoring
• AIMS Tutoring
• HSPT Tutoring
• ISAT Tutoring
• SSAT Tutoring

Search 50+ Tests

Loading Page

math tutoring

• Elementary Math
• Pre-Calculus
• Trigonometry

science tutoring

Foreign languages.

• Mandarin Chinese

elementary tutoring

• Computer Science

Search 350+ Subjects

• Video Overview
• Tutor Selection Process
• Online Tutoring
• Mobile Tutoring
• Instant Tutoring
• How We Operate
• Our Guarantee
• Impact of Tutoring
• Reviews & Testimonials
• Media Coverage
• About Varsity Tutors

ACT Math : How to find out when an equation has no solution

Study concepts, example questions & explanations for act math, all act math resources, example questions, example question #1 : how to find out when an equation has no solution.

Given the following system, find the solution:

2x – 2y = 2

no solution

When 2 equations in a system have the same slopes, they will either have no solution or infinite solutions. Since the y-intercepts are not the same, there is no solution to this system.

Example Question #2 : How To Find Out When An Equation Has No Solution

Infinite Solutions 

No solution

Like other "solve for x" problems, to begin it, the goal is to get x by itself on one side of the equals sign. In this problem, before doing so, the imaginary -1 in front of (-27x+27) must be distributed. 

Once this is done, you may start to try to get x by itself.

However, when subtracting 27x from either side and doing the same on the other,  the 27x term cancels out. As a result, the equation becomes:

We know this is an untrue statement because these numbers are 5 spaces away from each other on the number line. The final answer is No Solution . 

With the equations in this form, we can see that they have the same slope, but different y-intercepts.  Therefore, there is no solution to this system.

Example Question #4 : How To Find Out When An Equation Has No Solution

Infinite solutions

We know this is an untrue statement, so there is no solution to this equation.

Example Question #3 : How To Find Out When An Equation Has No Solution

Find the solution to the following equation if x = 3: 

y = (4x 2 - 2)/(9 - x 2 )

no possible solution

Substituting 3 in for x, you will get 0 in the denominator of the fraction. It is not possible to have 0 be the denominator for a fraction so there is no possible solution to this equation.

Example Question #5 : How To Find Out When An Equation Has No Solution

There is no solution

Example Question #6 : How To Find Out When An Equation Has No Solution

None of the other answers

A fraction is considered undefined when the denominator equals 0. Set the denominator equal to zero and solve for the variable.

Example Question #131 : Gre Quantitative Reasoning

No solutions.

Example Question #1 : Linear / Rational / Variable Equations

I, II, and III

II and III only

First, distribute, making sure to watch for negatives. 

Combine like terms. 

Subtract 7x from both sides. 

Add 18 on both sides and be careful adding integers. 

Report an issue with this question

If you've found an issue with this question, please let us know. With the help of the community we can continue to improve our educational resources.

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC 101 S. Hanley Rd, Suite 300 St. Louis, MO 63105

Or fill out the form below:

Contact Information

Complaint details.

Solving for a Variable:

Equations with infinite solutions and equations with no solution.

Not all equations we try to solve will end with \({\text{x}}\) = a specific number. Some equations may have infinitely many solutions and other equations may have no solution at all. The following video will show how to recognize these solutions.

Video Source (05:35 mins) | Transcript

There are 3 types of answers we can get when solving for a variable:

• \({\text{x}}\) = a specific number (this is what we’ve been getting until now such as \({\text{x}}=5.3\))
• \({\text{x}}\) = all real numbers or infinitely many solutions (when we get \({\text{x}}={\text{x}}\) or when any number is equal to itself such as \(3=3\))
• No Solutions (when we end with a false statement like \(1=5\))

Additional Resources

• Khan Academy: Number of Solutions to Equations (05:26 mins, Transcript )
• Khan Academy: Number of Solutions - Example (01:54 mins, Transcript )

Practice Problems

• \(-9{\text{M}} {-} 4 = -9{\text{M}} - 4\)
• \(9 + 8{\text{T}} = 13{\text{T}} + 2\)
• \(-4 + 2{\text{b}} = 2{\text{b}} - 9\)
• \(-7 + 7{\text{b}} + 18 = 3{\text{b}} + 3 - 4{\text{b}}\)
• \(2{\text{x}} + 5 + {\text{x}} = -1 + 3{\text{x}} + 6\)
• \(2(3{\text{X}} + 4) = 6{\text{X}} + 7\)
• \(-4(4{\text{M}} {-} 3) = -16{\text{M}} + 12\)

In this example, the first thing we need to do is combine like terms. This means we combine the terms with the variable \({\text{M}}\) with each other and we combine the terms without a variable together.

Note: There are two versions or ways to solve this equation. Either one is acceptable. You do not have to do both.

First version: Combine terms with variable \({\text{M}}\) first

There is currently a \(-9{\text{M}}\) on the right-hand side of the equation. We can remove it from the right-hand side and combine it with the left-hand side by adding \(+9{\text{M}}\) to both sides of the equation

On the right-hand side:

\(-9{\text{M}} + 9{\text{M}} = 0\) leaving just \(-4\)

On the left-hand side:

Because \(-9{\text{M}} + 9{\text{M}} = 0\), we are left with \(-4 = -4\). This statement is always true, therefore, there are infinitely many solutions for the equation \(-9{\text{M}} {-} 4 = -9{\text{M}} - 4\). This means that any value of \({\text{M}}\) will still make this equation true

Our final solution: Infinitely many solutions

Second version: Combine terms without a variable first

We want to combine the \(-4\) on the left-hand side of the equation with the \(-4\) on the right-hand side of the equation. To do this, add \(+4\) to both sides of the equation.

\(-4 + 4 = 0\)

This leaves us with \(-9{\text{M}}=-9{\text{M}}\). We can either stop here because we see both sides are equal to each other, which means that for any value of \({\text{M}}\) the statement will be true, or we can keep solving for \({\text{M}}\).

To keep solving for \({\text{M}}\), we need to multiply both sides by the multiplicative inverse of \(-9\). Multiply both sides by \(-\frac{1}{9}\).

\(\left (-\frac{1}{9} \right )\left ( -9 \right )=1\)

This leaves \(1{\text{M}} = 1{\text{M}}\).

\({\text{M}}={\text{M}}\) is always true for any value of \({\text{M}}\).

Our final solution: Infinitely Many Solutions

• One Solution

We start by combining like terms.

Combine the terms with the variable b by adding \(-2{\text{b}}\) to both sides of the equation.

Since \(2{\text{b}} + (-2{\text{b}}) = 0\), we are left with \(-4\) on the left-hand side and \(-9\) on the right-hand side.

But \(-4\) does not equal \(-9\).

This means that no matter what values we put into this equation, it is not true.

Our final solution: No solution

• Infinitely Many Solutions
• No Solution ( Solution Video | Transcript )
• Infinitely Many Solutions ( Solution Video | Transcript )

What Does It Mean When An Equation Has No Solution?

Sometimes equations have no solution. This means that no matter what value is plugged in for the variable, you will ALWAYS get a contradiction. Watch this tutorial and learn what it takes for an equation to have no solution.

• contradiction
• unequal sides
• no solution
• different sides
• sides never equal
• group variables
• variables cancel

Background Tutorials

Introduction to algebraic expressions.

What is a Variable?

You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!

Further Exploration

Identity equations and equations with no solution.

How Do You Solve an Equation with No Solution?

Trying to solve an equation with variables on both sides of the equation? Figure out how to get those variables together and solve the equation with this tutorial! Surprise! Turns out, this equation has no solution. Check out this tutorial and see why!

Systems with No Solution

How Do You Graph a System of Equations With No Solution?

There are many different ways to solve a system of linear equations. In this tutorial, you'll see how to solve a system of linear equations by graphing both lines and finding their intersection. Take a look!

• Terms of Use

• Bipolar Disorder
• Therapy Center
• When To See a Therapist
• Types of Therapy
• Best Online Therapy
• Best Couples Therapy
• Best Family Therapy
• Managing Stress
• Sleep and Dreaming
• Understanding Emotions
• Self-Improvement
• Healthy Relationships
• Student Resources
• Personality Types
• Guided Meditations
• Verywell Mind Insights
• 2024 Verywell Mind 25
• Mental Health in the Classroom
• Editorial Process
• Meet Our Review Board
• Crisis Support

Overview of the Problem-Solving Mental Process

Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

Rachel Goldman, PhD FTOS, is a licensed psychologist, clinical assistant professor, speaker, wellness expert specializing in eating behaviors, stress management, and health behavior change.

• Identify the Problem
• Define the Problem
• Form a Strategy
• Organize Information
• Allocate Resources
• Monitor Progress
• Evaluate the Results

Frequently Asked Questions

Problem-solving is a mental process that involves discovering, analyzing, and solving problems. The ultimate goal of problem-solving is to overcome obstacles and find a solution that best resolves the issue.

The best strategy for solving a problem depends largely on the unique situation. In some cases, people are better off learning everything they can about the issue and then using factual knowledge to come up with a solution. In other instances, creativity and insight are the best options.

It is not necessary to follow problem-solving steps sequentially, It is common to skip steps or even go back through steps multiple times until the desired solution is reached.

In order to correctly solve a problem, it is often important to follow a series of steps. Researchers sometimes refer to this as the problem-solving cycle. While this cycle is portrayed sequentially, people rarely follow a rigid series of steps to find a solution.

The following steps include developing strategies and organizing knowledge.

1. Identifying the Problem

While it may seem like an obvious step, identifying the problem is not always as simple as it sounds. In some cases, people might mistakenly identify the wrong source of a problem, which will make attempts to solve it inefficient or even useless.

Some strategies that you might use to figure out the source of a problem include :

• Asking questions about the problem
• Breaking the problem down into smaller pieces
• Looking at the problem from different perspectives
• Conducting research to figure out what relationships exist between different variables

2. Defining the Problem

After the problem has been identified, it is important to fully define the problem so that it can be solved. You can define a problem by operationally defining each aspect of the problem and setting goals for what aspects of the problem you will address

At this point, you should focus on figuring out which aspects of the problems are facts and which are opinions. State the problem clearly and identify the scope of the solution.

3. Forming a Strategy

After the problem has been identified, it is time to start brainstorming potential solutions. This step usually involves generating as many ideas as possible without judging their quality. Once several possibilities have been generated, they can be evaluated and narrowed down.

The next step is to develop a strategy to solve the problem. The approach used will vary depending upon the situation and the individual's unique preferences. Common problem-solving strategies include heuristics and algorithms.

• Heuristics are mental shortcuts that are often based on solutions that have worked in the past. They can work well if the problem is similar to something you have encountered before and are often the best choice if you need a fast solution.
• Algorithms are step-by-step strategies that are guaranteed to produce a correct result. While this approach is great for accuracy, it can also consume time and resources.

Heuristics are often best used when time is of the essence, while algorithms are a better choice when a decision needs to be as accurate as possible.

4. Organizing Information

Before coming up with a solution, you need to first organize the available information. What do you know about the problem? What do you not know? The more information that is available the better prepared you will be to come up with an accurate solution.

When approaching a problem, it is important to make sure that you have all the data you need. Making a decision without adequate information can lead to biased or inaccurate results.

5. Allocating Resources

Of course, we don't always have unlimited money, time, and other resources to solve a problem. Before you begin to solve a problem, you need to determine how high priority it is.

If it is an important problem, it is probably worth allocating more resources to solving it. If, however, it is a fairly unimportant problem, then you do not want to spend too much of your available resources on coming up with a solution.

At this stage, it is important to consider all of the factors that might affect the problem at hand. This includes looking at the available resources, deadlines that need to be met, and any possible risks involved in each solution. After careful evaluation, a decision can be made about which solution to pursue.

6. Monitoring Progress

After selecting a problem-solving strategy, it is time to put the plan into action and see if it works. This step might involve trying out different solutions to see which one is the most effective.

It is also important to monitor the situation after implementing a solution to ensure that the problem has been solved and that no new problems have arisen as a result of the proposed solution.

Effective problem-solvers tend to monitor their progress as they work towards a solution. If they are not making good progress toward reaching their goal, they will reevaluate their approach or look for new strategies .

7. Evaluating the Results

After a solution has been reached, it is important to evaluate the results to determine if it is the best possible solution to the problem. This evaluation might be immediate, such as checking the results of a math problem to ensure the answer is correct, or it can be delayed, such as evaluating the success of a therapy program after several months of treatment.

Once a problem has been solved, it is important to take some time to reflect on the process that was used and evaluate the results. This will help you to improve your problem-solving skills and become more efficient at solving future problems.

A Word From Verywell​

It is important to remember that there are many different problem-solving processes with different steps, and this is just one example. Problem-solving in real-world situations requires a great deal of resourcefulness, flexibility, resilience, and continuous interaction with the environment.

Get Advice From The Verywell Mind Podcast

Hosted by therapist Amy Morin, LCSW, this episode of The Verywell Mind Podcast shares how you can stop dwelling in a negative mindset.

Follow Now : Apple Podcasts / Spotify / Google Podcasts

You can become a better problem solving by:

• Practicing brainstorming and coming up with multiple potential solutions to problems
• Being open-minded and considering all possible options before making a decision
• Breaking down problems into smaller, more manageable pieces
• Asking for help when needed
• Researching different problem-solving techniques and trying out new ones
• Learning from mistakes and using them as opportunities to grow

It's important to communicate openly and honestly with your partner about what's going on. Try to see things from their perspective as well as your own. Work together to find a resolution that works for both of you. Be willing to compromise and accept that there may not be a perfect solution.

Take breaks if things are getting too heated, and come back to the problem when you feel calm and collected. Don't try to fix every problem on your own—consider asking a therapist or counselor for help and insight.

If you've tried everything and there doesn't seem to be a way to fix the problem, you may have to learn to accept it. This can be difficult, but try to focus on the positive aspects of your life and remember that every situation is temporary. Don't dwell on what's going wrong—instead, think about what's going right. Find support by talking to friends or family. Seek professional help if you're having trouble coping.

Davidson JE, Sternberg RJ, editors.  The Psychology of Problem Solving .  Cambridge University Press; 2003. doi:10.1017/CBO9780511615771

Sarathy V. Real world problem-solving .  Front Hum Neurosci . 2018;12:261. Published 2018 Jun 26. doi:10.3389/fnhum.2018.00261

By Kendra Cherry, MSEd Kendra Cherry, MS, is a psychosocial rehabilitation specialist, psychology educator, and author of the "Everything Psychology Book."

35 problem-solving techniques and methods for solving complex problems

Design your next session with SessionLab

Join the 150,000+ facilitators 
using SessionLab.

Recommended Articles

A step-by-step guide to planning a workshop, how to create an unforgettable training session in 8 simple steps, 47 useful online tools for workshop planning and meeting facilitation.

All teams and organizations encounter challenges as they grow. There are problems that might occur for teams when it comes to miscommunication or resolving business-critical issues . You may face challenges around growth , design , user engagement, and even team culture and happiness. In short, problem-solving techniques should be part of every team’s skillset.

Problem-solving methods are primarily designed to help a group or team through a process of first identifying problems and challenges , ideating possible solutions , and then evaluating the most suitable .

Finding effective solutions to complex problems isn’t easy, but by using the right process and techniques, you can help your team be more efficient in the process.

So how do you develop strategies that are engaging, and empower your team to solve problems effectively?

In this blog post, we share a series of problem-solving tools you can use in your next workshop or team meeting. You’ll also find some tips for facilitating the process and how to enable others to solve complex problems.

Let’s get started! 

How do you identify problems?

How do you identify the right solution.

• Tips for more effective problem-solving

Complete problem-solving methods

• Problem-solving techniques to identify and analyze problems
• Problem-solving techniques for developing solutions

Problem-solving warm-up activities

Closing activities for a problem-solving process.

Before you can move towards finding the right solution for a given problem, you first need to identify and define the problem you wish to solve. 

Here, you want to clearly articulate what the problem is and allow your group to do the same. Remember that everyone in a group is likely to have differing perspectives and alignment is necessary in order to help the group move forward. 

Identifying a problem accurately also requires that all members of a group are able to contribute their views in an open and safe manner. It can be scary for people to stand up and contribute, especially if the problems or challenges are emotive or personal in nature. Be sure to try and create a psychologically safe space for these kinds of discussions.

Remember that problem analysis and further discussion are also important. Not taking the time to fully analyze and discuss a challenge can result in the development of solutions that are not fit for purpose or do not address the underlying issue.

Successfully identifying and then analyzing a problem means facilitating a group through activities designed to help them clearly and honestly articulate their thoughts and produce usable insight.

With this data, you might then produce a problem statement that clearly describes the problem you wish to be addressed and also state the goal of any process you undertake to tackle this issue.  

Finding solutions is the end goal of any process. Complex organizational challenges can only be solved with an appropriate solution but discovering them requires using the right problem-solving tool.

After you’ve explored a problem and discussed ideas, you need to help a team discuss and choose the right solution. Consensus tools and methods such as those below help a group explore possible solutions before then voting for the best. They’re a great way to tap into the collective intelligence of the group for great results!

Remember that the process is often iterative. Great problem solvers often roadtest a viable solution in a measured way to see what works too. While you might not get the right solution on your first try, the methods below help teams land on the most likely to succeed solution while also holding space for improvement.

Every effective problem solving process begins with an agenda . A well-structured workshop is one of the best methods for successfully guiding a group from exploring a problem to implementing a solution.

In SessionLab, it’s easy to go from an idea to a complete agenda . Start by dragging and dropping your core problem solving activities into place . Add timings, breaks and necessary materials before sharing your agenda with your colleagues.

The resulting agenda will be your guide to an effective and productive problem solving session that will also help you stay organized on the day!

Tips for more effective problem solving

Problem-solving activities are only one part of the puzzle. While a great method can help unlock your team’s ability to solve problems, without a thoughtful approach and strong facilitation the solutions may not be fit for purpose.

Let’s take a look at some problem-solving tips you can apply to any process to help it be a success!

Clearly define the problem

Jumping straight to solutions can be tempting, though without first clearly articulating a problem, the solution might not be the right one. Many of the problem-solving activities below include sections where the problem is explored and clearly defined before moving on.

This is a vital part of the problem-solving process and taking the time to fully define an issue can save time and effort later. A clear definition helps identify irrelevant information and it also ensures that your team sets off on the right track.

Don’t jump to conclusions

It’s easy for groups to exhibit cognitive bias or have preconceived ideas about both problems and potential solutions. Be sure to back up any problem statements or potential solutions with facts, research, and adequate forethought.

The best techniques ask participants to be methodical and challenge preconceived notions. Make sure you give the group enough time and space to collect relevant information and consider the problem in a new way. By approaching the process with a clear, rational mindset, you’ll often find that better solutions are more forthcoming.  

Try different approaches  

Problems come in all shapes and sizes and so too should the methods you use to solve them. If you find that one approach isn’t yielding results and your team isn’t finding different solutions, try mixing it up. You’ll be surprised at how using a new creative activity can unblock your team and generate great solutions.

Don’t take it personally 

Depending on the nature of your team or organizational problems, it’s easy for conversations to get heated. While it’s good for participants to be engaged in the discussions, ensure that emotions don’t run too high and that blame isn’t thrown around while finding solutions.

You’re all in it together, and even if your team or area is seeing problems, that isn’t necessarily a disparagement of you personally. Using facilitation skills to manage group dynamics is one effective method of helping conversations be more constructive.

Get the right people in the room

Your problem-solving method is often only as effective as the group using it. Getting the right people on the job and managing the number of people present is important too!

If the group is too small, you may not get enough different perspectives to effectively solve a problem. If the group is too large, you can go round and round during the ideation stages.

Creating the right group makeup is also important in ensuring you have the necessary expertise and skillset to both identify and follow up on potential solutions. Carefully consider who to include at each stage to help ensure your problem-solving method is followed and positioned for success.

Document everything

The best solutions can take refinement, iteration, and reflection to come out. Get into a habit of documenting your process in order to keep all the learnings from the session and to allow ideas to mature and develop. Many of the methods below involve the creation of documents or shared resources. Be sure to keep and share these so everyone can benefit from the work done!

Bring a facilitator 

Facilitation is all about making group processes easier. With a subject as potentially emotive and important as problem-solving, having an impartial third party in the form of a facilitator can make all the difference in finding great solutions and keeping the process moving. Consider bringing a facilitator to your problem-solving session to get better results and generate meaningful solutions!

Develop your problem-solving skills

It takes time and practice to be an effective problem solver. While some roles or participants might more naturally gravitate towards problem-solving, it can take development and planning to help everyone create better solutions.

You might develop a training program, run a problem-solving workshop or simply ask your team to practice using the techniques below. Check out our post on problem-solving skills to see how you and your group can develop the right mental process and be more resilient to issues too!

Design a great agenda

Workshops are a great format for solving problems. With the right approach, you can focus a group and help them find the solutions to their own problems. But designing a process can be time-consuming and finding the right activities can be difficult.

Check out our workshop planning guide to level-up your agenda design and start running more effective workshops. Need inspiration? Check out templates designed by expert facilitators to help you kickstart your process!

In this section, we’ll look at in-depth problem-solving methods that provide a complete end-to-end process for developing effective solutions. These will help guide your team from the discovery and definition of a problem through to delivering the right solution.

If you’re looking for an all-encompassing method or problem-solving model, these processes are a great place to start. They’ll ask your team to challenge preconceived ideas and adopt a mindset for solving problems more effectively.

• Six Thinking Hats
• Lightning Decision Jam
• Problem Definition Process
• Discovery & Action Dialogue

Design Sprint 2.0

• Open Space Technology

1. Six Thinking Hats

Individual approaches to solving a problem can be very different based on what team or role an individual holds. It can be easy for existing biases or perspectives to find their way into the mix, or for internal politics to direct a conversation.

Six Thinking Hats is a classic method for identifying the problems that need to be solved and enables your team to consider them from different angles, whether that is by focusing on facts and data, creative solutions, or by considering why a particular solution might not work.

Like all problem-solving frameworks, Six Thinking Hats is effective at helping teams remove roadblocks from a conversation or discussion and come to terms with all the aspects necessary to solve complex problems.

2. Lightning Decision Jam

Featured courtesy of Jonathan Courtney of AJ&Smart Berlin, Lightning Decision Jam is one of those strategies that should be in every facilitation toolbox. Exploring problems and finding solutions is often creative in nature, though as with any creative process, there is the potential to lose focus and get lost.

Unstructured discussions might get you there in the end, but it’s much more effective to use a method that creates a clear process and team focus.

In Lightning Decision Jam, participants are invited to begin by writing challenges, concerns, or mistakes on post-its without discussing them before then being invited by the moderator to present them to the group.

From there, the team vote on which problems to solve and are guided through steps that will allow them to reframe those problems, create solutions and then decide what to execute on. 

By deciding the problems that need to be solved as a team before moving on, this group process is great for ensuring the whole team is aligned and can take ownership over the next stages. 

Lightning Decision Jam (LDJ)   #action   #decision making   #problem solving   #issue analysis   #innovation   #design   #remote-friendly   The problem with anything that requires creative thinking is that it’s easy to get lost—lose focus and fall into the trap of having useless, open-ended, unstructured discussions. Here’s the most effective solution I’ve found: Replace all open, unstructured discussion with a clear process. What to use this exercise for: Anything which requires a group of people to make decisions, solve problems or discuss challenges. It’s always good to frame an LDJ session with a broad topic, here are some examples: The conversion flow of our checkout Our internal design process How we organise events Keeping up with our competition Improving sales flow

3. Problem Definition Process

While problems can be complex, the problem-solving methods you use to identify and solve those problems can often be simple in design. 

By taking the time to truly identify and define a problem before asking the group to reframe the challenge as an opportunity, this method is a great way to enable change.

Begin by identifying a focus question and exploring the ways in which it manifests before splitting into five teams who will each consider the problem using a different method: escape, reversal, exaggeration, distortion or wishful. Teams develop a problem objective and create ideas in line with their method before then feeding them back to the group.

This method is great for enabling in-depth discussions while also creating space for finding creative solutions too!

Problem Definition   #problem solving   #idea generation   #creativity   #online   #remote-friendly   A problem solving technique to define a problem, challenge or opportunity and to generate ideas.

4. The 5 Whys 

Sometimes, a group needs to go further with their strategies and analyze the root cause at the heart of organizational issues. An RCA or root cause analysis is the process of identifying what is at the heart of business problems or recurring challenges. 

The 5 Whys is a simple and effective method of helping a group go find the root cause of any problem or challenge and conduct analysis that will deliver results. 

By beginning with the creation of a problem statement and going through five stages to refine it, The 5 Whys provides everything you need to truly discover the cause of an issue.

The 5 Whys   #hyperisland   #innovation   This simple and powerful method is useful for getting to the core of a problem or challenge. As the title suggests, the group defines a problems, then asks the question “why” five times, often using the resulting explanation as a starting point for creative problem solving.

5. World Cafe

World Cafe is a simple but powerful facilitation technique to help bigger groups to focus their energy and attention on solving complex problems.

World Cafe enables this approach by creating a relaxed atmosphere where participants are able to self-organize and explore topics relevant and important to them which are themed around a central problem-solving purpose. Create the right atmosphere by modeling your space after a cafe and after guiding the group through the method, let them take the lead!

Making problem-solving a part of your organization’s culture in the long term can be a difficult undertaking. More approachable formats like World Cafe can be especially effective in bringing people unfamiliar with workshops into the fold. 

World Cafe   #hyperisland   #innovation   #issue analysis   World Café is a simple yet powerful method, originated by Juanita Brown, for enabling meaningful conversations driven completely by participants and the topics that are relevant and important to them. Facilitators create a cafe-style space and provide simple guidelines. Participants then self-organize and explore a set of relevant topics or questions for conversation.

6. Discovery & Action Dialogue (DAD)

One of the best approaches is to create a safe space for a group to share and discover practices and behaviors that can help them find their own solutions.

With DAD, you can help a group choose which problems they wish to solve and which approaches they will take to do so. It’s great at helping remove resistance to change and can help get buy-in at every level too!

This process of enabling frontline ownership is great in ensuring follow-through and is one of the methods you will want in your toolbox as a facilitator.

Discovery & Action Dialogue (DAD)   #idea generation   #liberating structures   #action   #issue analysis   #remote-friendly   DADs make it easy for a group or community to discover practices and behaviors that enable some individuals (without access to special resources and facing the same constraints) to find better solutions than their peers to common problems. These are called positive deviant (PD) behaviors and practices. DADs make it possible for people in the group, unit, or community to discover by themselves these PD practices. DADs also create favorable conditions for stimulating participants’ creativity in spaces where they can feel safe to invent new and more effective practices. Resistance to change evaporates as participants are unleashed to choose freely which practices they will adopt or try and which problems they will tackle. DADs make it possible to achieve frontline ownership of solutions.

7. Design Sprint 2.0

Want to see how a team can solve big problems and move forward with prototyping and testing solutions in a few days? The Design Sprint 2.0 template from Jake Knapp, author of Sprint, is a complete agenda for a with proven results.

Developing the right agenda can involve difficult but necessary planning. Ensuring all the correct steps are followed can also be stressful or time-consuming depending on your level of experience.

Use this complete 4-day workshop template if you are finding there is no obvious solution to your challenge and want to focus your team around a specific problem that might require a shortcut to launching a minimum viable product or waiting for the organization-wide implementation of a solution.

8. Open space technology

Open space technology- developed by Harrison Owen – creates a space where large groups are invited to take ownership of their problem solving and lead individual sessions. Open space technology is a great format when you have a great deal of expertise and insight in the room and want to allow for different takes and approaches on a particular theme or problem you need to be solved.

Start by bringing your participants together to align around a central theme and focus their efforts. Explain the ground rules to help guide the problem-solving process and then invite members to identify any issue connecting to the central theme that they are interested in and are prepared to take responsibility for.

Once participants have decided on their approach to the core theme, they write their issue on a piece of paper, announce it to the group, pick a session time and place, and post the paper on the wall. As the wall fills up with sessions, the group is then invited to join the sessions that interest them the most and which they can contribute to, then you’re ready to begin!

Everyone joins the problem-solving group they’ve signed up to, record the discussion and if appropriate, findings can then be shared with the rest of the group afterward.

Open Space Technology   #action plan   #idea generation   #problem solving   #issue analysis   #large group   #online   #remote-friendly   Open Space is a methodology for large groups to create their agenda discerning important topics for discussion, suitable for conferences, community gatherings and whole system facilitation

Techniques to identify and analyze problems

Using a problem-solving method to help a team identify and analyze a problem can be a quick and effective addition to any workshop or meeting.

While further actions are always necessary, you can generate momentum and alignment easily, and these activities are a great place to get started.

We’ve put together this list of techniques to help you and your team with problem identification, analysis, and discussion that sets the foundation for developing effective solutions.

Let’s take a look!

• The Creativity Dice
• Fishbone Analysis
• Problem Tree
• SWOT Analysis
• Agreement-Certainty Matrix
• The Journalistic Six
• LEGO Challenge
• What, So What, Now What?
• Journalists

Individual and group perspectives are incredibly important, but what happens if people are set in their minds and need a change of perspective in order to approach a problem more effectively?

Flip It is a method we love because it is both simple to understand and run, and allows groups to understand how their perspectives and biases are formed. 

Participants in Flip It are first invited to consider concerns, issues, or problems from a perspective of fear and write them on a flip chart. Then, the group is asked to consider those same issues from a perspective of hope and flip their understanding.  

No problem and solution is free from existing bias and by changing perspectives with Flip It, you can then develop a problem solving model quickly and effectively.

Flip It!   #gamestorming   #problem solving   #action   Often, a change in a problem or situation comes simply from a change in our perspectives. Flip It! is a quick game designed to show players that perspectives are made, not born.

10. The Creativity Dice

One of the most useful problem solving skills you can teach your team is of approaching challenges with creativity, flexibility, and openness. Games like The Creativity Dice allow teams to overcome the potential hurdle of too much linear thinking and approach the process with a sense of fun and speed. 

In The Creativity Dice, participants are organized around a topic and roll a dice to determine what they will work on for a period of 3 minutes at a time. They might roll a 3 and work on investigating factual information on the chosen topic. They might roll a 1 and work on identifying the specific goals, standards, or criteria for the session.

Encouraging rapid work and iteration while asking participants to be flexible are great skills to cultivate. Having a stage for idea incubation in this game is also important. Moments of pause can help ensure the ideas that are put forward are the most suitable. 

The Creativity Dice   #creativity   #problem solving   #thiagi   #issue analysis   Too much linear thinking is hazardous to creative problem solving. To be creative, you should approach the problem (or the opportunity) from different points of view. You should leave a thought hanging in mid-air and move to another. This skipping around prevents premature closure and lets your brain incubate one line of thought while you consciously pursue another.

11. Fishbone Analysis

Organizational or team challenges are rarely simple, and it’s important to remember that one problem can be an indication of something that goes deeper and may require further consideration to be solved.

Fishbone Analysis helps groups to dig deeper and understand the origins of a problem. It’s a great example of a root cause analysis method that is simple for everyone on a team to get their head around. 

Participants in this activity are asked to annotate a diagram of a fish, first adding the problem or issue to be worked on at the head of a fish before then brainstorming the root causes of the problem and adding them as bones on the fish. 

Using abstractions such as a diagram of a fish can really help a team break out of their regular thinking and develop a creative approach.

Fishbone Analysis   #problem solving   ##root cause analysis   #decision making   #online facilitation   A process to help identify and understand the origins of problems, issues or observations.

12. Problem Tree 

Encouraging visual thinking can be an essential part of many strategies. By simply reframing and clarifying problems, a group can move towards developing a problem solving model that works for them. 

In Problem Tree, groups are asked to first brainstorm a list of problems – these can be design problems, team problems or larger business problems – and then organize them into a hierarchy. The hierarchy could be from most important to least important or abstract to practical, though the key thing with problem solving games that involve this aspect is that your group has some way of managing and sorting all the issues that are raised.

Once you have a list of problems that need to be solved and have organized them accordingly, you’re then well-positioned for the next problem solving steps.

Problem tree   #define intentions   #create   #design   #issue analysis   A problem tree is a tool to clarify the hierarchy of problems addressed by the team within a design project; it represents high level problems or related sublevel problems.

13. SWOT Analysis

Chances are you’ve heard of the SWOT Analysis before. This problem-solving method focuses on identifying strengths, weaknesses, opportunities, and threats is a tried and tested method for both individuals and teams.

Start by creating a desired end state or outcome and bare this in mind – any process solving model is made more effective by knowing what you are moving towards. Create a quadrant made up of the four categories of a SWOT analysis and ask participants to generate ideas based on each of those quadrants.

Once you have those ideas assembled in their quadrants, cluster them together based on their affinity with other ideas. These clusters are then used to facilitate group conversations and move things forward. 

SWOT analysis   #gamestorming   #problem solving   #action   #meeting facilitation   The SWOT Analysis is a long-standing technique of looking at what we have, with respect to the desired end state, as well as what we could improve on. It gives us an opportunity to gauge approaching opportunities and dangers, and assess the seriousness of the conditions that affect our future. When we understand those conditions, we can influence what comes next.

14. Agreement-Certainty Matrix

Not every problem-solving approach is right for every challenge, and deciding on the right method for the challenge at hand is a key part of being an effective team.

The Agreement Certainty matrix helps teams align on the nature of the challenges facing them. By sorting problems from simple to chaotic, your team can understand what methods are suitable for each problem and what they can do to ensure effective results. 

If you are already using Liberating Structures techniques as part of your problem-solving strategy, the Agreement-Certainty Matrix can be an invaluable addition to your process. We’ve found it particularly if you are having issues with recurring problems in your organization and want to go deeper in understanding the root cause. 

Agreement-Certainty Matrix   #issue analysis   #liberating structures   #problem solving   You can help individuals or groups avoid the frequent mistake of trying to solve a problem with methods that are not adapted to the nature of their challenge. The combination of two questions makes it possible to easily sort challenges into four categories: simple, complicated, complex , and chaotic .  A problem is simple when it can be solved reliably with practices that are easy to duplicate.  It is complicated when experts are required to devise a sophisticated solution that will yield the desired results predictably.  A problem is complex when there are several valid ways to proceed but outcomes are not predictable in detail.  Chaotic is when the context is too turbulent to identify a path forward.  A loose analogy may be used to describe these differences: simple is like following a recipe, complicated like sending a rocket to the moon, complex like raising a child, and chaotic is like the game “Pin the Tail on the Donkey.”  The Liberating Structures Matching Matrix in Chapter 5 can be used as the first step to clarify the nature of a challenge and avoid the mismatches between problems and solutions that are frequently at the root of chronic, recurring problems.

Organizing and charting a team’s progress can be important in ensuring its success. SQUID (Sequential Question and Insight Diagram) is a great model that allows a team to effectively switch between giving questions and answers and develop the skills they need to stay on track throughout the process. 

Begin with two different colored sticky notes – one for questions and one for answers – and with your central topic (the head of the squid) on the board. Ask the group to first come up with a series of questions connected to their best guess of how to approach the topic. Ask the group to come up with answers to those questions, fix them to the board and connect them with a line. After some discussion, go back to question mode by responding to the generated answers or other points on the board.

It’s rewarding to see a diagram grow throughout the exercise, and a completed SQUID can provide a visual resource for future effort and as an example for other teams.

SQUID   #gamestorming   #project planning   #issue analysis   #problem solving   When exploring an information space, it’s important for a group to know where they are at any given time. By using SQUID, a group charts out the territory as they go and can navigate accordingly. SQUID stands for Sequential Question and Insight Diagram.

16. Speed Boat

To continue with our nautical theme, Speed Boat is a short and sweet activity that can help a team quickly identify what employees, clients or service users might have a problem with and analyze what might be standing in the way of achieving a solution.

Methods that allow for a group to make observations, have insights and obtain those eureka moments quickly are invaluable when trying to solve complex problems.

In Speed Boat, the approach is to first consider what anchors and challenges might be holding an organization (or boat) back. Bonus points if you are able to identify any sharks in the water and develop ideas that can also deal with competitors!   

Speed Boat   #gamestorming   #problem solving   #action   Speedboat is a short and sweet way to identify what your employees or clients don’t like about your product/service or what’s standing in the way of a desired goal.

17. The Journalistic Six

Some of the most effective ways of solving problems is by encouraging teams to be more inclusive and diverse in their thinking.

Based on the six key questions journalism students are taught to answer in articles and news stories, The Journalistic Six helps create teams to see the whole picture. By using who, what, when, where, why, and how to facilitate the conversation and encourage creative thinking, your team can make sure that the problem identification and problem analysis stages of the are covered exhaustively and thoughtfully. Reporter’s notebook and dictaphone optional.

The Journalistic Six – Who What When Where Why How   #idea generation   #issue analysis   #problem solving   #online   #creative thinking   #remote-friendly   A questioning method for generating, explaining, investigating ideas.

18. LEGO Challenge

Now for an activity that is a little out of the (toy) box. LEGO Serious Play is a facilitation methodology that can be used to improve creative thinking and problem-solving skills. 

The LEGO Challenge includes giving each member of the team an assignment that is hidden from the rest of the group while they create a structure without speaking.

What the LEGO challenge brings to the table is a fun working example of working with stakeholders who might not be on the same page to solve problems. Also, it’s LEGO! Who doesn’t love LEGO! 

LEGO Challenge   #hyperisland   #team   A team-building activity in which groups must work together to build a structure out of LEGO, but each individual has a secret “assignment” which makes the collaborative process more challenging. It emphasizes group communication, leadership dynamics, conflict, cooperation, patience and problem solving strategy.

19. What, So What, Now What?

If not carefully managed, the problem identification and problem analysis stages of the problem-solving process can actually create more problems and misunderstandings.

The What, So What, Now What? problem-solving activity is designed to help collect insights and move forward while also eliminating the possibility of disagreement when it comes to identifying, clarifying, and analyzing organizational or work problems. 

Facilitation is all about bringing groups together so that might work on a shared goal and the best problem-solving strategies ensure that teams are aligned in purpose, if not initially in opinion or insight.

Throughout the three steps of this game, you give everyone on a team to reflect on a problem by asking what happened, why it is important, and what actions should then be taken. 

This can be a great activity for bringing our individual perceptions about a problem or challenge and contextualizing it in a larger group setting. This is one of the most important problem-solving skills you can bring to your organization.

W³ – What, So What, Now What?   #issue analysis   #innovation   #liberating structures   You can help groups reflect on a shared experience in a way that builds understanding and spurs coordinated action while avoiding unproductive conflict. It is possible for every voice to be heard while simultaneously sifting for insights and shaping new direction. Progressing in stages makes this practical—from collecting facts about What Happened to making sense of these facts with So What and finally to what actions logically follow with Now What . The shared progression eliminates most of the misunderstandings that otherwise fuel disagreements about what to do. Voila!

20. Journalists  

Problem analysis can be one of the most important and decisive stages of all problem-solving tools. Sometimes, a team can become bogged down in the details and are unable to move forward.

Journalists is an activity that can avoid a group from getting stuck in the problem identification or problem analysis stages of the process.

In Journalists, the group is invited to draft the front page of a fictional newspaper and figure out what stories deserve to be on the cover and what headlines those stories will have. By reframing how your problems and challenges are approached, you can help a team move productively through the process and be better prepared for the steps to follow.

Journalists   #vision   #big picture   #issue analysis   #remote-friendly   This is an exercise to use when the group gets stuck in details and struggles to see the big picture. Also good for defining a vision.

Problem-solving techniques for developing solutions 

The success of any problem-solving process can be measured by the solutions it produces. After you’ve defined the issue, explored existing ideas, and ideated, it’s time to narrow down to the correct solution.

Use these problem-solving techniques when you want to help your team find consensus, compare possible solutions, and move towards taking action on a particular problem.

• Improved Solutions
• Four-Step Sketch
• 15% Solutions
• How-Now-Wow matrix
• Impact Effort Matrix

21. Mindspin  

Brainstorming is part of the bread and butter of the problem-solving process and all problem-solving strategies benefit from getting ideas out and challenging a team to generate solutions quickly. 

With Mindspin, participants are encouraged not only to generate ideas but to do so under time constraints and by slamming down cards and passing them on. By doing multiple rounds, your team can begin with a free generation of possible solutions before moving on to developing those solutions and encouraging further ideation. 

This is one of our favorite problem-solving activities and can be great for keeping the energy up throughout the workshop. Remember the importance of helping people become engaged in the process – energizing problem-solving techniques like Mindspin can help ensure your team stays engaged and happy, even when the problems they’re coming together to solve are complex. 

MindSpin   #teampedia   #idea generation   #problem solving   #action   A fast and loud method to enhance brainstorming within a team. Since this activity has more than round ideas that are repetitive can be ruled out leaving more creative and innovative answers to the challenge.

22. Improved Solutions

After a team has successfully identified a problem and come up with a few solutions, it can be tempting to call the work of the problem-solving process complete. That said, the first solution is not necessarily the best, and by including a further review and reflection activity into your problem-solving model, you can ensure your group reaches the best possible result. 

One of a number of problem-solving games from Thiagi Group, Improved Solutions helps you go the extra mile and develop suggested solutions with close consideration and peer review. By supporting the discussion of several problems at once and by shifting team roles throughout, this problem-solving technique is a dynamic way of finding the best solution. 

Improved Solutions   #creativity   #thiagi   #problem solving   #action   #team   You can improve any solution by objectively reviewing its strengths and weaknesses and making suitable adjustments. In this creativity framegame, you improve the solutions to several problems. To maintain objective detachment, you deal with a different problem during each of six rounds and assume different roles (problem owner, consultant, basher, booster, enhancer, and evaluator) during each round. At the conclusion of the activity, each player ends up with two solutions to her problem.

23. Four Step Sketch

Creative thinking and visual ideation does not need to be confined to the opening stages of your problem-solving strategies. Exercises that include sketching and prototyping on paper can be effective at the solution finding and development stage of the process, and can be great for keeping a team engaged. 

By going from simple notes to a crazy 8s round that involves rapidly sketching 8 variations on their ideas before then producing a final solution sketch, the group is able to iterate quickly and visually. Problem-solving techniques like Four-Step Sketch are great if you have a group of different thinkers and want to change things up from a more textual or discussion-based approach.

Four-Step Sketch   #design sprint   #innovation   #idea generation   #remote-friendly   The four-step sketch is an exercise that helps people to create well-formed concepts through a structured process that includes: Review key information Start design work on paper,  Consider multiple variations , Create a detailed solution . This exercise is preceded by a set of other activities allowing the group to clarify the challenge they want to solve. See how the Four Step Sketch exercise fits into a Design Sprint

24. 15% Solutions

Some problems are simpler than others and with the right problem-solving activities, you can empower people to take immediate actions that can help create organizational change. 

Part of the liberating structures toolkit, 15% solutions is a problem-solving technique that focuses on finding and implementing solutions quickly. A process of iterating and making small changes quickly can help generate momentum and an appetite for solving complex problems.

Problem-solving strategies can live and die on whether people are onboard. Getting some quick wins is a great way of getting people behind the process.   

It can be extremely empowering for a team to realize that problem-solving techniques can be deployed quickly and easily and delineate between things they can positively impact and those things they cannot change. 

15% Solutions   #action   #liberating structures   #remote-friendly   You can reveal the actions, however small, that everyone can do immediately. At a minimum, these will create momentum, and that may make a BIG difference.  15% Solutions show that there is no reason to wait around, feel powerless, or fearful. They help people pick it up a level. They get individuals and the group to focus on what is within their discretion instead of what they cannot change.  With a very simple question, you can flip the conversation to what can be done and find solutions to big problems that are often distributed widely in places not known in advance. Shifting a few grains of sand may trigger a landslide and change the whole landscape.

25. How-Now-Wow Matrix

The problem-solving process is often creative, as complex problems usually require a change of thinking and creative response in order to find the best solutions. While it’s common for the first stages to encourage creative thinking, groups can often gravitate to familiar solutions when it comes to the end of the process. 

When selecting solutions, you don’t want to lose your creative energy! The How-Now-Wow Matrix from Gamestorming is a great problem-solving activity that enables a group to stay creative and think out of the box when it comes to selecting the right solution for a given problem.

Problem-solving techniques that encourage creative thinking and the ideation and selection of new solutions can be the most effective in organisational change. Give the How-Now-Wow Matrix a go, and not just for how pleasant it is to say out loud. 

How-Now-Wow Matrix   #gamestorming   #idea generation   #remote-friendly   When people want to develop new ideas, they most often think out of the box in the brainstorming or divergent phase. However, when it comes to convergence, people often end up picking ideas that are most familiar to them. This is called a ‘creative paradox’ or a ‘creadox’. The How-Now-Wow matrix is an idea selection tool that breaks the creadox by forcing people to weigh each idea on 2 parameters.

26. Impact and Effort Matrix

All problem-solving techniques hope to not only find solutions to a given problem or challenge but to find the best solution. When it comes to finding a solution, groups are invited to put on their decision-making hats and really think about how a proposed idea would work in practice. 

The Impact and Effort Matrix is one of the problem-solving techniques that fall into this camp, empowering participants to first generate ideas and then categorize them into a 2×2 matrix based on impact and effort.

Activities that invite critical thinking while remaining simple are invaluable. Use the Impact and Effort Matrix to move from ideation and towards evaluating potential solutions before then committing to them. 

Impact and Effort Matrix   #gamestorming   #decision making   #action   #remote-friendly   In this decision-making exercise, possible actions are mapped based on two factors: effort required to implement and potential impact. Categorizing ideas along these lines is a useful technique in decision making, as it obliges contributors to balance and evaluate suggested actions before committing to them.

27. Dotmocracy

If you’ve followed each of the problem-solving steps with your group successfully, you should move towards the end of your process with heaps of possible solutions developed with a specific problem in mind. But how do you help a group go from ideation to putting a solution into action? 

Dotmocracy – or Dot Voting -is a tried and tested method of helping a team in the problem-solving process make decisions and put actions in place with a degree of oversight and consensus. 

One of the problem-solving techniques that should be in every facilitator’s toolbox, Dot Voting is fast and effective and can help identify the most popular and best solutions and help bring a group to a decision effectively. 

Dotmocracy   #action   #decision making   #group prioritization   #hyperisland   #remote-friendly   Dotmocracy is a simple method for group prioritization or decision-making. It is not an activity on its own, but a method to use in processes where prioritization or decision-making is the aim. The method supports a group to quickly see which options are most popular or relevant. The options or ideas are written on post-its and stuck up on a wall for the whole group to see. Each person votes for the options they think are the strongest, and that information is used to inform a decision.

All facilitators know that warm-ups and icebreakers are useful for any workshop or group process. Problem-solving workshops are no different.

Use these problem-solving techniques to warm up a group and prepare them for the rest of the process. Activating your group by tapping into some of the top problem-solving skills can be one of the best ways to see great outcomes from your session.

• Check-in/Check-out
• Doodling Together
• Show and Tell
• Constellations
• Draw a Tree

28. Check-in / Check-out

Solid processes are planned from beginning to end, and the best facilitators know that setting the tone and establishing a safe, open environment can be integral to a successful problem-solving process.

Check-in / Check-out is a great way to begin and/or bookend a problem-solving workshop. Checking in to a session emphasizes that everyone will be seen, heard, and expected to contribute. 

If you are running a series of meetings, setting a consistent pattern of checking in and checking out can really help your team get into a groove. We recommend this opening-closing activity for small to medium-sized groups though it can work with large groups if they’re disciplined!

Check-in / Check-out   #team   #opening   #closing   #hyperisland   #remote-friendly   Either checking-in or checking-out is a simple way for a team to open or close a process, symbolically and in a collaborative way. Checking-in/out invites each member in a group to be present, seen and heard, and to express a reflection or a feeling. Checking-in emphasizes presence, focus and group commitment; checking-out emphasizes reflection and symbolic closure.

29. Doodling Together  

Thinking creatively and not being afraid to make suggestions are important problem-solving skills for any group or team, and warming up by encouraging these behaviors is a great way to start. 

Doodling Together is one of our favorite creative ice breaker games – it’s quick, effective, and fun and can make all following problem-solving steps easier by encouraging a group to collaborate visually. By passing cards and adding additional items as they go, the workshop group gets into a groove of co-creation and idea development that is crucial to finding solutions to problems. 

Doodling Together   #collaboration   #creativity   #teamwork   #fun   #team   #visual methods   #energiser   #icebreaker   #remote-friendly   Create wild, weird and often funny postcards together & establish a group’s creative confidence.

30. Show and Tell

You might remember some version of Show and Tell from being a kid in school and it’s a great problem-solving activity to kick off a session.

Asking participants to prepare a little something before a workshop by bringing an object for show and tell can help them warm up before the session has even begun! Games that include a physical object can also help encourage early engagement before moving onto more big-picture thinking.

By asking your participants to tell stories about why they chose to bring a particular item to the group, you can help teams see things from new perspectives and see both differences and similarities in the way they approach a topic. Great groundwork for approaching a problem-solving process as a team! 

Show and Tell   #gamestorming   #action   #opening   #meeting facilitation   Show and Tell taps into the power of metaphors to reveal players’ underlying assumptions and associations around a topic The aim of the game is to get a deeper understanding of stakeholders’ perspectives on anything—a new project, an organizational restructuring, a shift in the company’s vision or team dynamic.

31. Constellations

Who doesn’t love stars? Constellations is a great warm-up activity for any workshop as it gets people up off their feet, energized, and ready to engage in new ways with established topics. It’s also great for showing existing beliefs, biases, and patterns that can come into play as part of your session.

Using warm-up games that help build trust and connection while also allowing for non-verbal responses can be great for easing people into the problem-solving process and encouraging engagement from everyone in the group. Constellations is great in large spaces that allow for movement and is definitely a practical exercise to allow the group to see patterns that are otherwise invisible. 

Constellations   #trust   #connection   #opening   #coaching   #patterns   #system   Individuals express their response to a statement or idea by standing closer or further from a central object. Used with teams to reveal system, hidden patterns, perspectives.

32. Draw a Tree

Problem-solving games that help raise group awareness through a central, unifying metaphor can be effective ways to warm-up a group in any problem-solving model.

Draw a Tree is a simple warm-up activity you can use in any group and which can provide a quick jolt of energy. Start by asking your participants to draw a tree in just 45 seconds – they can choose whether it will be abstract or realistic. 

Once the timer is up, ask the group how many people included the roots of the tree and use this as a means to discuss how we can ignore important parts of any system simply because they are not visible.

All problem-solving strategies are made more effective by thinking of problems critically and by exposing things that may not normally come to light. Warm-up games like Draw a Tree are great in that they quickly demonstrate some key problem-solving skills in an accessible and effective way.

Draw a Tree   #thiagi   #opening   #perspectives   #remote-friendly   With this game you can raise awarness about being more mindful, and aware of the environment we live in.

Each step of the problem-solving workshop benefits from an intelligent deployment of activities, games, and techniques. Bringing your session to an effective close helps ensure that solutions are followed through on and that you also celebrate what has been achieved.

Here are some problem-solving activities you can use to effectively close a workshop or meeting and ensure the great work you’ve done can continue afterward.

• One Breath Feedback
• Who What When Matrix
• Response Cards

How do I conclude a problem-solving process?

All good things must come to an end. With the bulk of the work done, it can be tempting to conclude your workshop swiftly and without a moment to debrief and align. This can be problematic in that it doesn’t allow your team to fully process the results or reflect on the process.

At the end of an effective session, your team will have gone through a process that, while productive, can be exhausting. It’s important to give your group a moment to take a breath, ensure that they are clear on future actions, and provide short feedback before leaving the space. 

The primary purpose of any problem-solving method is to generate solutions and then implement them. Be sure to take the opportunity to ensure everyone is aligned and ready to effectively implement the solutions you produced in the workshop.

Remember that every process can be improved and by giving a short moment to collect feedback in the session, you can further refine your problem-solving methods and see further success in the future too.

33. One Breath Feedback

Maintaining attention and focus during the closing stages of a problem-solving workshop can be tricky and so being concise when giving feedback can be important. It’s easy to incur “death by feedback” should some team members go on for too long sharing their perspectives in a quick feedback round. 

One Breath Feedback is a great closing activity for workshops. You give everyone an opportunity to provide feedback on what they’ve done but only in the space of a single breath. This keeps feedback short and to the point and means that everyone is encouraged to provide the most important piece of feedback to them. 

One breath feedback   #closing   #feedback   #action   This is a feedback round in just one breath that excels in maintaining attention: each participants is able to speak during just one breath … for most people that’s around 20 to 25 seconds … unless of course you’ve been a deep sea diver in which case you’ll be able to do it for longer.

34. Who What When Matrix 

Matrices feature as part of many effective problem-solving strategies and with good reason. They are easily recognizable, simple to use, and generate results.

The Who What When Matrix is a great tool to use when closing your problem-solving session by attributing a who, what and when to the actions and solutions you have decided upon. The resulting matrix is a simple, easy-to-follow way of ensuring your team can move forward. 

Great solutions can’t be enacted without action and ownership. Your problem-solving process should include a stage for allocating tasks to individuals or teams and creating a realistic timeframe for those solutions to be implemented or checked out. Use this method to keep the solution implementation process clear and simple for all involved. 

Who/What/When Matrix   #gamestorming   #action   #project planning   With Who/What/When matrix, you can connect people with clear actions they have defined and have committed to.

35. Response cards

Group discussion can comprise the bulk of most problem-solving activities and by the end of the process, you might find that your team is talked out! 

Providing a means for your team to give feedback with short written notes can ensure everyone is head and can contribute without the need to stand up and talk. Depending on the needs of the group, giving an alternative can help ensure everyone can contribute to your problem-solving model in the way that makes the most sense for them.

Response Cards is a great way to close a workshop if you are looking for a gentle warm-down and want to get some swift discussion around some of the feedback that is raised. 

Response Cards   #debriefing   #closing   #structured sharing   #questions and answers   #thiagi   #action   It can be hard to involve everyone during a closing of a session. Some might stay in the background or get unheard because of louder participants. However, with the use of Response Cards, everyone will be involved in providing feedback or clarify questions at the end of a session.

Save time and effort discovering the right solutions

A structured problem solving process is a surefire way of solving tough problems, discovering creative solutions and driving organizational change. But how can you design for successful outcomes?

With SessionLab, it’s easy to design engaging workshops that deliver results. Drag, drop and reorder blocks  to build your agenda. When you make changes or update your agenda, your session  timing   adjusts automatically , saving you time on manual adjustments.

Collaborating with stakeholders or clients? Share your agenda with a single click and collaborate in real-time. No more sending documents back and forth over email.

Explore  how to use SessionLab  to design effective problem solving workshops or  watch this five minute video  to see the planner in action!

Over to you

The problem-solving process can often be as complicated and multifaceted as the problems they are set-up to solve. With the right problem-solving techniques and a mix of creative exercises designed to guide discussion and generate purposeful ideas, we hope we’ve given you the tools to find the best solutions as simply and easily as possible.

Is there a problem-solving technique that you are missing here? Do you have a favorite activity or method you use when facilitating? Let us know in the comments below, we’d love to hear from you! 

thank you very much for these excellent techniques

Certainly wonderful article, very detailed. Shared!

Your list of techniques for problem solving can be helpfully extended by adding TRIZ to the list of techniques. TRIZ has 40 problem solving techniques derived from methods inventros and patent holders used to get new patents. About 10-12 are general approaches. many organization sponsor classes in TRIZ that are used to solve business problems or general organiztational problems. You can take a look at TRIZ and dwonload a free internet booklet to see if you feel it shound be included per your selection process.

Leave a Comment Cancel reply

Your email address will not be published. Required fields are marked *

Going from a mere idea to a workshop that delivers results for your clients can feel like a daunting task. In this piece, we will shine a light on all the work behind the scenes and help you learn how to plan a workshop from start to finish. On a good day, facilitation can feel like effortless magic, but that is mostly the result of backstage work, foresight, and a lot of careful planning. Read on to learn a step-by-step approach to breaking the process of planning a workshop into small, manageable chunks.  The flow starts with the first meeting with a client to define the purposes of a workshop.…

How does learning work? A clever 9-year-old once told me: “I know I am learning something new when I am surprised.” The science of adult learning tells us that, in order to learn new skills (which, unsurprisingly, is harder for adults to do than kids) grown-ups need to first get into a specific headspace.  In a business, this approach is often employed in a training session where employees learn new skills or work on professional development. But how do you ensure your training is effective? In this guide, we'll explore how to create an effective training session plan and run engaging training sessions. As team leader, project manager, or consultant,…

Effective online tools are a necessity for smooth and engaging virtual workshops and meetings. But how do you choose the right ones? Do you sometimes feel that the good old pen and paper or MS Office toolkit and email leaves you struggling to stay on top of managing and delivering your workshop? Fortunately, there are plenty of online tools to make your life easier when you need to facilitate a meeting and lead workshops. In this post, we’ll share our favorite online tools you can use to make your job as a facilitator easier. In fact, there are plenty of free online workshop tools and meeting facilitation software you can…

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• High School Math Solutions – Radical Equation Calculator Radical equations are equations involving radicals of any order. We will show examples of square roots; higher...

Please add a message.

Message received. Thanks for the feedback.

Self-Esteem

It’s ok you can’t solve every problem, trying to “fix" everything can leave you feeling like a failure..

Updated May 10, 2024 | Reviewed by Ray Parker

• What Is Self-Esteem?
• Find a therapist near me
• Your intrinsic value is more than what you can do for other people.

You are still worthwhile and can be successful, even if you don’t have all the solutions.

• Consider which decision will make you feel you’ve stayed true to your values.

In coaching others, I often discuss problem-solving strategies to help individuals think creatively and consider many options when they are faced with challenging situations.

Problem solving 1-2 includes the following:

• Define the problem, identify obstacles, and set realistic goals .
• Generate a variety of alternative solutions to overcome obstacles identified.
• Choose which idea has the highest likelihood to achieve the goal.
• Try out the solution in real-life and see if it worked or not.

Problem-solving strategies can be helpful in many situations. Thinking creatively and testing out different potential solutions can help you come up with alternative ways of solving your problems.

While many problems can be solved, there are also situations in which there is no “perfect” solution or in which what seems to be the best solution still leaves you feeling unsatisfied or like you’re not doing enough.

I encourage you to increase your comfort around the following three truths:

1. You can’t always solve everyone else’s problems.

2. You can’t always solve all of your own problems.

3. You are not a failure if you can’t solve every problem.

You can’t always solve everyone else’s problems.

When someone around you needs help, do you feel compelled to find solutions to their problem?

Are you seen as the problem solver at your job or in your close relationships?

Does it feel uncomfortable for you to listen to someone tell you about a problem and not offer solutions?

There are times when others come to you because they know you can help them solve a problem. There are also times when the other person is coming to you not for a solution to their problem, but for support, empathy, and a listening ear.

Your relationships may be negatively impacted if others feel that you don’t fully listen and only try to “fix” everything for them. While this may feel like a noble act, it may lead the other person to feel like they have failed or that you think they are unable to solve their own problems.

Consider approaching such situations with curiosity by saying to the other person:

• As you share this information with me, tell me how I can best support you.
• What would be most helpful right now? Are you looking for an empathetic ear or want to brainstorm potential next steps?
• I want to be sure I am as helpful as I can be right now; what are you hoping to get out of our conversation?

You can’t always solve all of your own problems.

We are taught from a young age that problems have a solution. For example, while solving word problems in math class may not have been your favorite thing to do, you knew there was ultimately a “right” answer. Many times, the real world is much more complex, and many of the problems that you face do not have clear or “right” answers.

You may often be faced with finding solutions that do the most good for the most amount of people, but you know that others may still be left out or feel unsatisfied with the result.

Your beliefs about yourself, other people, and the world can sometimes help you make decisions in such circumstances. You may ask for help from others. Some may consider their faith or spirituality for guidance. While others may consider philosophical theories.

Knowing that there often isn’t a “perfect” solution, you may consider asking yourself some of the following questions:

• What’s the healthiest decision I can make? The healthiest decision for yourself and for those who will be impacted.
• Imagine yourself 10 years in the future, looking back on the situation: What do you think the future-you would encourage you to do?
• What would a wise person do?
• What decision will allow you to feel like you’ve stayed true to your values?

You are not a failure if you can’t solve all of the problems.

If you have internalized feeling like you need to be able to solve every problem that comes across your path, you may feel like a failure each time you don’t.

It’s impossible to solve every problem.

Your intrinsic value is more than what you can do for other people. You have value because you are you.

Consider creating more realistic and adaptive thoughts around your ability to help others and solve problems.

Some examples include:

• I am capable, even without solving all of the problems.
• I am worthwhile, even if I’m not perfect.
• What I do for others does not define my worth.
• In living my values, I know I’ve done my best.

I hope you utilize the information above to consider how you can coach yourself the next time you:

• Start to solve someone else’s problem without being asked.
• Feel stuck in deciding the best next steps.
• Judge yourself negatively.

1. D'zurilla, T. J., & Goldfried, M. R. (1971). Problem solving and behavior modification. Journal of abnormal psychology, 78(1), 107.

2. D’Zurilla, T. J., & Nezu, A. M. (2010). Problem-solving therapy. Handbook of cognitive-behavioral therapies, 3(1), 197-225.

Julie Radico, Psy.D. ABPP, is a board-certified clinical psychologist and coauthor of You Will Get Through This: A Mental Health First-Aid Kit.

• Find a Therapist
• Find a Treatment Center
• Find a Psychiatrist
• Find a Support Group
• Find Online Therapy
• United States
• Brooklyn, NY
• Chicago, IL
• Houston, TX
• Los Angeles, CA
• New York, NY
• Portland, OR
• San Diego, CA
• San Francisco, CA
• Seattle, WA
• Washington, DC
• Asperger's
• Bipolar Disorder
• Chronic Pain
• Eating Disorders
• Passive Aggression
• Personality
• Goal Setting
• Positive Psychology
• Stopping Smoking
• Low Sexual Desire
• Relationships
• Child Development
• Therapy Center NEW
• Diagnosis Dictionary
• Types of Therapy

At any moment, someone’s aggravating behavior or our own bad luck can set us off on an emotional spiral that threatens to derail our entire day. Here’s how we can face our triggers with less reactivity so that we can get on with our lives.

• Emotional Intelligence
• Gaslighting
• Affective Forecasting
• Neuroscience

Why Highway 1 is the climate challenge that California can’t fix

It is beloved by Big Sur road trippers and is vital for local businesses. But intense storms, slides and fires imperil this highway. What does the future hold?

BIG SUR, Calif. — Workers dangle from a crane, drilling into the vertical face of rock that holds up one of the most famous and picturesque stretches of road in the world. They’re performing a delicate surgery on fragile geology in hopes that a single lane of traffic can safely flow to Big Sur before summer arrives.

On this day, it had been nearly a month since a rockslide severed Highway 1, California’s beloved road-trip destination.

Across this stretch of the Central Coast, landslides have repeatedly buried the highway’s undulating curves or sent pavement tumbling into the Pacific Ocean. They bring a steady drumbeat of road blockages, tourism disruptions and stranded communities. Now, some fear the landslides are getting worse, due to climate change and engineering missteps throughout the roadway’s 86-year life span.

It was always a risky proposition to maintain a highway at the very edge of a continent. But now Big Sur is facing wetter storms that infiltrate and weaken cracked and porous rock. Wildfires leave behind extra debris for those floodwaters to carry downhill. Pounding waves from stronger storms and rising seas eat away at cliffs from beneath.

“Everything is working against Highway 1,” said Gary Griggs, an oceanography professor at the University of California at Santa Cruz.

The latest slip-out, known as the Rocky Creek slide, exemplifies the complexity of the problem. It stranded 1,500 people at the end of March as workers were making slow progress addressing three other slides. California’s transportation agency — known as CalTrans — estimates it will take more than $100 million to fix them all — if new slides don’t come first.

California is a national leader in confronting climate change, but making Highway 1 sustainable may be a challenge it cannot surmount. Despite spending a billion dollars a year to fix damage that climate-related stressors inflict on its roadways — plus $100 million in projects to make infrastructure more resilient to climate change — the state is struggling to fortify one of its most prized landmarks.

Some have suggested rerouting Highway 1 inland, but they don’t understand its terrain, or its identity, said state Sen. John Laird (D), a former California natural resources secretary who represents part of the Central Coast in the state legislature. Barriers and boulders armor sections of the road and the cliffs against erosion, but extending those interventions along some 100 miles of highway isn’t feasible, others say.

That leaves few options: Get better at predicting and fixing the landslides, and preventing them when possible. Or else imagine the unthinkable: Giving up on maintaining a continuous 656-mile stretch of blacktop from Orange County to Mendocino County, and letting parts of Highway 1 become dead ends.

CalTrans routinely patrols the cliffsides and deploys remote sensing for signs of movement to predict where the next slide might occur. It is repairing the latest section of crumbled highway with an eye toward the climate of the future, officials said.

“As we rebuild we have to do so with the knowledge that the conditions that have washed out sections of roadway will become more and more common in the future,” CalTrans officials said in a statement. “We have to prepare for that.”

But still, the agency did not expect the most recent slide would hit when and where it did. It’s like a high-stakes game of whack-a-mole — one in which, Laird said, Mother Nature and climate change keep upping the ante.

For now, there is no option but to keep knocking down the obstacles as they come. Nearly everyone interviewed for this article said California wouldn’t be California without this road.

“Of course we have to keep it alive,” Laird said.

A fragile foundation for a highway

The most landslide prone stretch of Highway 1, from around Hearst Castle in San Simeon to Carmel-by-the-Sea and the Monterey Peninsula, has for decades epitomized California’s reputation for scenic and rugged landscapes. It’s where road trippers can get a view of dense redwoods out of one window and crashing waves out of the other, often at the edge of cliffs as much as 500 feet above the beach.

For decades, this region has attracted artists and others seeking beauty and isolation. As the author Henry Miller once wrote, “Big Sur has a climate all its own and a character all its own.”

More recently, the rise of Instagram and selfie culture has helped fuel a crushing surge in tourists to its 33 bridges and postcard-like coastlines to look for whales, sea lions and elephant seals.

“Big Sur’s massive popularity is damaging the very scenic qualities and natural beauty that make the area so precious,” said a 2020 CalTrans study of the highway.

But now, it’s geology that is perhaps more threatening.

The ground has been shaky beneath this stretch of Highway 1 ever since it started carrying traffic in 1937, crossing over diverse rock formations that are still in their adolescence, geologically speaking.

Deep down sits the hard crystalline base of the Sierra Nevada some 150 miles to the east. On top of that are layers of sedimentary rock left over from an older mountain range. And then, mixed within, there are shreds of shale like volcanic rocks that were scraped up from the ocean floor as two tectonic plates clashed.

“It’s as if that area went through a blender,” said Jon Warrick, a Santa Cruz-based research geologist for the U.S. Geological Survey.

In older parts of the continent, such as the East Coast, rock formations are older and denser, and therefore not prone to movement. But in Big Sur, gaps and joints still exist from when the rocks first came together along the nearby San Andreas fault, and other secondary faults in the area.

This is the country’s steepest coastline outside of Alaska, according to Kevin Schmidt, another USGS geologist, and when these formations are exposed to the elements, their fragility becomes evident.

Water trickles — and sometimes pours — into the cracks between rocks, reaching layers of clay-rich rock crushed as finely as flour. It turns them into a slick slurry — a recipe for landslides.

Climate change compounds the problem

Climate change has only juiced up those ingredients. Take what happened in 2017, when one of the region’s wettest winters in a century interrupted an extended drought.

Weeks of heavy January and February rains saturated a mountainside that was already imperceptibly sliding above Highway 1, until, by May, the instability became too much. In an instant, so much earth poured down steep slopes near Mud Creek, the USGS said, that it was enough to “fill a line of dump trucks nearly a thousand miles long.”

It took more than a year and $54 million to reconnect Big Sur communities to points south.

Though it took experts by surprise, Griggs said it shouldn’t have. Two decades earlier, CalTrans had declared the area “very active,” with “high landslide potential” due to weaker bedrock and unstable construction.

The slides often occur weeks, if not months, after rainy weather, with about 90 percent of the region’s rain typically falling between November and April. Geologists add that the stormy pattern of the last two years — the 2022-2023 winter brought record-setting amounts of precipitation — has compounded landslide risks.

Much of that increased rain is likely to come through juiced-up storms known as atmospheric rivers, which can pummel California’s coasts in winter months, sometimes one after another. But even without those, the state is seeing more thunderstorms typical in other parts of the country but less so in California, said Daniel Swain, a climate scientist at UCLA. California, including Big Sur, is seeing precipitation events that are about 10 percent more intense statewide than they have been historically, he said.

Add it all up, and it appears a trend of bigger and more frequent landslides is coming, Warrick added, if it isn’t already here.

Big Sur Island

The latest Highway 1 interruption feels all too familiar to Big Sur veterans, including Ben Perlmutter, whose family has lived in Big Sur for three generations.

Now 33, Perlmutter has experienced or heard stories about decades of disasters. In 1995, the National Guard had to erect a bridge to reconnect Big Sur to the outside world after a washout. In 1998, Highway 1 collapsed in five places and an Army helicopter had to rescue his family. In 2008, a wildfire ignited nearby, forcing them out of their home for more than a week. In 2017, a landslide closed the highway again, leaving residents cut off for nine months.

Now, “we can’t catch a break,” he said, explaining how the latest slide brought business that was already slow to a grinding halt. Residents can leave and enter Big Sur only in convoys at 7 a.m. and 5 p.m. Tourists, the town’s main source of income, have only recently been allowed in the convoys, and are visiting in much smaller numbers.

Perlmutter, who grew up behind the bar of his father’s restaurant, moved back home with his wife six months ago to take over the Big Sur River Inn from his 91-year-old father and remains unsure if he’s going to break even his first year.

“There is this fatigue level. … You have to totally transform on a dime to prepare your businesses to respond to these disasters,” Perlmutter said. “A lot of emotion goes into that.”

Even so, Perlmutter and other businesses owners have thrown themselves into community efforts since the latest slide.

Within 24 hours, Perlmutter said his bar manager, a volunteer firefighter and EMT, quickly coordinated places for 1,500 stranded tourists to sleep. The Big Sur River Inn has also hosted a Taco Tuesday, practically giving away food and drinks so they didn’t go to waste. Deetjen’s, another historic inn, has also been serving discounted community breakfasts. Musicians have been playing impromptu shows, for a distraction.

Yet these charitable responses can endure for only so long. Costs of doing business keep rising in Big Sur, and bigger corporations continue to move in and subsume long-standing family operations.

“You feel like you are in a rodeo getting bucked continuously,” said Kirk Gafill, who also grew up in a landmark restaurant that he now runs, called Nepenthe. “You are constantly calling on reserves, never knowing what is going to happen.”

No permanent solution

Preserving the Big Sur that residents and tourists love sometimes seems like a fantasy venture.

To prepare for bigger storms and help water run off the cliffs, CalTrans officials told The Washington Post they are replacing and enlarging stormwater culverts. They are engineering ways to strengthen the roadway and the cliffs it sits upon.

But sometimes such engineering isn’t possible because of concerns for wildlife, such as an endangered snail known as the black abalone. And it cannot last forever. Longtime residents and officials say that along the rocky coast, walls built during the 1980s to stabilize the road have since eroded and withered away.

CalTrans officials said they have no long-term scheme for maintaining the highway, other than tackling landslides as they emerge and preventing them whenever possible.

But sometimes, there is nothing that could keep cliffs upright. There was a concrete wall at the base of a bridge over Rocky Creek, site of the latest slide, for example. Now, to get a single lane of traffic flowing again, workers are hammering vertical and horizontal supports deep within the cliff and reinforcing it with a sprayed-on material known as shotcrete.

A permanent fix is unrealistic, Griggs said. Even if California turned Highway 1 into a toll road — like the famous 17-Mile Drive on the nearby Monterey Peninsula — all the money in the world could not eliminate landslides, he said. “There are some problems we just don’t have solutions for,” he added.

California received some $375 million to prepare its highways for climate change through the federal bipartisan infrastructure law passed in 2021. While such spending is vital, Laird said, his single Senate district — one of 40 statewide — has transportation needs that could easily consume billions of dollars.

From his perspective, the state should be spending all it can to preserve Highway 1 and access to Bug Sur because it epitomizes what is so unique about California. “It’s a natural mecca,” he said.

Others foresee a day when such investment becomes foolish and preservation becomes impossible. Cheryl Hapke helped lead study of the geology beneath Highway 1, spending 22 years as a USGS research scientist working closely with CalTrans in studying landslide risks. By now, she said, communities continually finding themselves stranded may need to think about relocating.

“I’m not saying do it tomorrow, but at some point, the conversation probably has to be had,” said Hapke, now a Florida-based principal consultant in coastal resiliency for Fugro, an environmental consulting firm.

“We’re living with what we’ve created in this changing climate,” she added. “There’s answers. They’re not easy.”

• My Kaspersky
• My Products / Subscriptions
• Solutions for:

Privacy & Kids

Kaspersky Password Manager: now with an authenticator

The already impressive list of Kaspersky Password Manager features has been expanded to include a built-in, cross-platform, two-factor authentication code generator.

Kaspersky Team

August 21, 2023

More great news: our recently updated Kaspersky Password Manager  now has a built-in function for generating one-time codes for two-factor authentication (2FA). This means no more installing a separate authenticator app — everything you need is right there in our password manager. Now for a few details…

What’s an authenticator?

On this blog, we focus quite a bit on 2FA — app-generated one-time codes in particular. Over the past couple of years, we’ve posted a whole series of materials on this topic, the most important of which make for highly recommended reading:

• What is multi-factor authentication?
• Types of two-factor authentication: pros and cons
• Is Google Authenticator irreplaceable?
• Authentication with one-time codes: pros and cons
• The best authenticator apps for Android, iOS, Windows, and macOS

In a nutshell, you need 2FA to better protect your accounts, so we recommend enabling it on all services that support it. In our view, one-off codes generated in special authenticator apps strike the best balance between security and usability. Such a code must be entered after the regular password, and because it’s valid for a limited time (usually no more than 30 seconds), it’s extremely difficult to intercept.

The 2FA method is both quick and smooth, provides a high level of protection, and requires no additional input or time investment on the part of the user. Before, 2FA meant having an authenticator app on your device — either Google Authenticator or any other that suits you. Now, however, there’s no need to install an additional app: you can generate codes right inside Kaspersky Password Manager , where your passwords are already stored securely. Let’s take a look at the advantages of our built-in authenticator.

1. Familiar interface with cross-platform convenience

Kaspersky Password Manager  generates one-time codes in a familiar user-friendly way: in the special Authenticator section is a list of tokens with names and short descriptions, next to which one-time codes appear and a time counter ticks away until the next update of these codes. That’s similar to how it works in other apps, so you’ll have no trouble switching to Kaspersky Password Manager  if you already use another authenticator. That’s an obvious advantage, but far from the only one.

A massive plus compared to other authenticators is that Kaspersky Password Manager  gives you a universal, cross-platform, all-in-one solution — the app stores your passwords and generates one-time codes on whichever platform you prefer: computer or phone. Kaspersky Password Manager is available not only for Android and iOS, but also for macOS and Windows (support for 2FA code generation in Windows will be added in an upcoming update). The Windows version is especially important: if you’ve read our post about the best authenticator apps , you’ll have noticed that Windows is rather poorly served.

2. Synchronization and security

Next advantage: all Kaspersky Password Manager entries (passwords, notes, authenticator tokens, etc.) are automatically synchronized between all your devices. This allows you to generate an authentication code on any device you’re currently using.

Synchronization uses the cloud, of course, but with maximum security and convenience. For one thing, you don’t have to create an extra account — a My Kaspersky account is all that’s needed, which you already have if you use any of our products. And for another, all authentication tokens are securely protected by the main password, without which no intruder can use your passwords or authenticator — even if they do somehow get inside your My Kaspersky account.

3. Don’t have your smartphone to hand? No problem!

Users of other authenticator apps face the eternal nightmare of leaving behind or, worse, losing their smartphone: recovering authentication tokens is so difficult that we even wrote a special step-by-step guide for that. Now, because Kaspersky Password Manager  securely stores your tokens (and with them all passwords) in encrypted form in the cloud, you can use the authenticator at any time on the device you’re using, as well as restore all data on a new device; all you have to remember is your main password.

4. Easy migration

Lastly, one other advantage of the built-in authenticator in Kaspersky Password Manager is quick and easy migration of all data from Google Authenticator. All you need to do is export all tokens from Google Authenticator to one large QR code in the usual way, then scan it in Kaspersky Password Manager  — everything will work right away.

As far as we know, no other authenticator app makes it so easy to migrate data from Google Authenticator; the process usually involves lots of sweat and tears as you painstakingly recreate all your tokens one by one. But with Kaspersky Password Manager , four taps on the screen are literally all it takes.

What else can Kaspersky Password Manager do?

Let’s wrap up with a few words about some other useful features in Kaspersky Password Manager  besides unbeatable password protection and the new built-in authenticator. This handy app can also:

• Autofill data in online forms — and not only usernames and passwords, but other information such as addresses and bank card details.
• Warn you if your password is too weak , was used before, or has been compromised in a known leak.
• Generate the strongest passwords possible based on customizable random character combinations.
• Securely store important documents, bank card details, and any other highly valuable information (for example, cryptowallet seed phrases).
• Encrypt all stored data with the robust AES-256 algorithm. The encryption key is created from the main password and is not stored anywhere , so without the main password it’s simply impossible to decrypt the contents of Kaspersky Password Manager .

Incidentally, the recent update of Kaspersky Password Manager  added not only a built-in authenticator, but also support for Opera and Opera GX browsers. So now you can autofill passwords and other data in all the most popular browsers out there: Chrome (and others based on Chromium), Safari, Firefox, Edge, and now Opera.

And remember, the full version of Kaspersky Password Manager comes included in the Kaspersky Plus and Kaspersky Premium subscriptions, along with the most reliable protection possible, unlimited VPN , and a host of other useful features .

Zenbleed: new hardware vulnerability in AMD CPUs

Explaining an issue in popular PC and server CPUs in simple terms.

Malware lurking in “official” GitHub and GitLab links

Can you catch malware by downloading files from Microsoft’s repositories on GitHub? Turns out, you can. Stay alert!

Advertisers sharing data about you with… intelligence agencies

Advertising firms’ extensive collection of personal data is becoming of great use to intelligence agencies. So how to guard against mass surveillance?

Residential proxies: understanding the risks for organizations

Proxyware can make it difficult to detect cyberattacks on organizations — sometimes making the latter unwitting accomplices in crimes.

Watch the (verified) birdie, or new ways to recognize fakes

How to tell a real photo or video from a fake, and trace its provenance.

Sign up to receive our headlines in your inbox

Home solutions.

• Kaspersky Standard
• Kaspersky Plus
• Kaspersky Premium
• All Solutions

Small Business Products

• Kaspersky Small Office Security
• Kaspersky Endpoint Security Cloud
• All Products

Medium Business Products

• Kaspersky Next
• Kaspersky Endpoint Security for Business Select
• Kaspersky Endpoint Security for Business Advanced