solving word problems for variables

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \mathrm{Lauren's\:age\:is\:half\:of\:Joe's\:age.\:Emma\:is\:four\:years\:older\:than\:Joe.\:The\:sum\:of\:Lauren,\:Emma,\:and\:Joe's\:age\:is\:54.\:How\:old\:is\:Joe?}
• \mathrm{Kira\:went\:for\:a\:drive\:in\:her\:new\:car.\:She\:drove\:for\:142.5\:miles\:at\:a\:speed\:of\:57\:mph.\:For\:how\:many\:hours\:did\:she\:drive?}
• \mathrm{The\:sum\:of\:two\:numbers\:is\:249\:.\:Twice\:the\:larger\:number\:plus\:three\:times\:the\:smaller\:number\:is\:591\:.\:Find\:the\:numbers.}
• \mathrm{If\:2\:tacos\:and\:3\:drinks\:cost\:12\:and\:3\:tacos\:and\:2\:drinks\:cost\:13\:how\:much\:does\:a\:taco\:cost?}
• \mathrm{You\:deposit\:3000\:in\:an\:account\:earning\:2\%\:interest\:compounded\:monthly.\:How\:much\:will\:you\:have\:in\:the\:account\:in\:15\:years?}
• How do you solve word problems?
• To solve word problems start by reading the problem carefully and understanding what it's asking. Try underlining or highlighting key information, such as numbers and key words that indicate what operation is needed to perform. Translate the problem into mathematical expressions or equations, and use the information and equations generated to solve for the answer.
• How do you identify word problems in math?
• Word problems in math can be identified by the use of language that describes a situation or scenario. Word problems often use words and phrases which indicate that performing calculations is needed to find a solution. Additionally, word problems will often include specific information such as numbers, measurements, and units that needed to be used to solve the problem.
• Is there a calculator that can solve word problems?
• Symbolab is the best calculator for solving a wide range of word problems, including age problems, distance problems, cost problems, investments problems, number problems, and percent problems.
• What is an age problem?
• An age problem is a type of word problem in math that involves calculating the age of one or more people at a specific point in time. These problems often use phrases such as 'x years ago,' 'in y years,' or 'y years later,' which indicate that the problem is related to time and age.

word-problems-calculator

• High School Math Solutions – Inequalities Calculator, Exponential Inequalities Last post, we talked about how to solve logarithmic inequalities. This post, we will learn how to solve exponential...

Please add a message.

Message received. Thanks for the feedback.

• Get started with computers
• Learn Microsoft Office
• Apply for a job
• Improve my work skills
• Design nice-looking docs
• Getting Started
• Smartphones & Tablets
• Typing Tutorial
• Online Learning
• Basic Internet Skills
• Online Safety
• Social Media
• Zoom Basics
• Google Docs
• Google Sheets
• Career Planning
• Resume Writing
• Cover Letters
• Job Search and Networking
• Business Communication
• Entrepreneurship 101
• Careers without College
• Job Hunt for Today
• 3D Printing
• Freelancing 101
• Personal Finance
• Sharing Economy
• Decision-Making
• Graphic Design
• Photography
• Image Editing
• Learning WordPress
• Language Learning
• Critical Thinking
• For Educators
• Translations
• Staff Picks
• English expand_more expand_less

Algebra Topics  - Introduction to Word Problems

Algebra topics  -, introduction to word problems, algebra topics introduction to word problems.

Algebra Topics: Introduction to Word Problems

Lesson 9: introduction to word problems.

/en/algebra-topics/solving-equations/content/

What are word problems?

A word problem is a math problem written out as a short story or scenario. Basically, it describes a realistic problem and asks you to imagine how you would solve it using math. If you've ever taken a math class, you've probably solved a word problem. For instance, does this sound familiar?

Johnny has 12 apples. If he gives four to Susie, how many will he have left?

You could solve this problem by looking at the numbers and figuring out what the problem is asking you to do. In this case, you're supposed to find out how many apples Johnny has left at the end of the problem. By reading the problem, you know Johnny starts out with 12 apples. By the end, he has 4 less because he gave them away. You could write this as:

12 - 4 = 8 , so you know Johnny has 8 apples left.

Word problems in algebra

If you were able to solve this problem, you should also be able to solve algebra word problems. Yes, they involve more complicated math, but they use the same basic problem-solving skills as simpler word problems.

You can tackle any word problem by following these five steps:

• Read through the problem carefully, and figure out what it's about.
• Represent unknown numbers with variables.
• Translate the rest of the problem into a mathematical expression.
• Solve the problem.
• Check your work.

We'll work through an algebra word problem using these steps. Here's a typical problem:

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took two days, and the van cost $360. How many miles did she drive?

It might seem complicated at first glance, but we already have all of the information we need to solve it. Let's go through it step by step.

Step 1: Read through the problem carefully.

With any problem, start by reading through the problem. As you're reading, consider:

• What question is the problem asking?
• What information do you already have?

Let's take a look at our problem again. What question is the problem asking? In other words, what are you trying to find out?

The rate to rent a small moving van is $30 per day, plus $0.50 per mile. Jada rented a van to drive to her new home. It took 2 days, and the van cost $360. How many miles did she drive?

There's only one question here. We're trying to find out how many miles Jada drove . Now we need to locate any information that will help us answer this question.

There are a few important things we know that will help us figure out the total mileage Jada drove:

• The van cost $30 per day.
• In addition to paying a daily charge, Jada paid $0.50 per mile.
• Jada had the van for 2 days.
• The total cost was $360 .

Step 2: Represent unknown numbers with variables.

In algebra, you represent unknown numbers with letters called variables . (To learn more about variables, see our lesson on reading algebraic expressions .) You can use a variable in the place of any amount you don't know. Looking at our problem, do you see a quantity we should represent with a variable? It's often the number we're trying to find out.

Since we're trying to find the total number of miles Jada drove, we'll represent that amount with a variable—at least until we know it. We'll use the variable m for miles . Of course, we could use any variable, but m should be easy to remember.

Step 3: Translate the rest of the problem.

Let's take another look at the problem, with the facts we'll use to solve it highlighted.

The rate to rent a small moving van is $30 per day , plus $0.50 per mile . Jada rented a van to drive to her new home. It took 2 days , and the van cost $360 . How many miles did she drive?

We know the total cost of the van, and we know that it includes a fee for the number of days, plus another fee for the number of miles. It's $30 per day, and $0.50 per mile. A simpler way to say this would be:

$30 per day plus $0.50 per mile is $360.

If you look at this sentence and the original problem, you can see that they basically say the same thing: It cost Jada $30 per day and $0.50 per mile, and her total cost was $360 . The shorter version will be easier to translate into a mathematical expression.

Let's start by translating $30 per day . To calculate the cost of something that costs a certain amount per day, you'd multiply the per-day cost by the number of days—in other words, 30 per day could be written as 30 ⋅ days, or 30 times the number of days . (Not sure why you'd translate it this way? Check out our lesson on writing algebraic expressions .)

$30 per day and $.50 per mile is $360

$30 ⋅ day + $.50 ⋅ mile = $360

As you can see, there were a few other words we could translate into operators, so and $.50 became + $.50 , $.50 per mile became $.50 ⋅ mile , and is became = .

Next, we'll add in the numbers and variables we already know. We already know the number of days Jada drove, 2 , so we can replace that. We've also already said we'll use m to represent the number of miles, so we can replace that too. We should also take the dollar signs off of the money amounts to make them consistent with the other numbers.

30 ⋅ 2 + .5 ⋅ m = 360

Now we have our expression. All that's left to do is solve it.

Step 4: Solve the problem.

This problem will take a few steps to solve. (If you're not sure how to do the math in this section, you might want to review our lesson on simplifying expressions .) First, let's simplify the expression as much as possible. We can multiply 30 and 2, so let's go ahead and do that. We can also write .5 ⋅ m as 0.5 m .

60 + .5m = 360

Next, we need to do what we can to get the m alone on the left side of the equals sign. Once we do that, we'll know what m is equal to—in other words, it will let us know the number of miles in our word problem.

We can start by getting rid of the 60 on the left side by subtracting it from both sides .

The only thing left to get rid of is .5 . Since it's being multiplied with m , we'll do the reverse and divide both sides of the equation with it.

.5 m / .5 is m and 300 / 0.50 is 600 , so m = 600 . In other words, the answer to our problem is 600 —we now know Jada drove 600 miles.

Step 5: Check the problem.

To make sure we solved the problem correctly, we should check our work. To do this, we can use the answer we just got— 600 —and calculate backward to find another of the quantities in our problem. In other words, if our answer for Jada's distance is correct, we should be able to use it to work backward and find another value, like the total cost. Let's take another look at the problem.

According to the problem, the van costs $30 per day and $0.50 per mile. If Jada really did drive 600 miles in 2 days, she could calculate the cost like this:

$30 per day and $0.50 per mile

30 ⋅ day + .5 ⋅ mile

30 ⋅ 2 + .5 ⋅ 600

According to our math, the van would cost $360, which is exactly what the problem says. This means our solution was correct. We're done!

While some word problems will be more complicated than others, you can use these basic steps to approach any word problem. On the next page, you can try it for yourself.

Let's practice with a couple more problems. You can solve these problems the same way we solved the first one—just follow the problem-solving steps we covered earlier. For your reference, these steps are:

If you get stuck, you might want to review the problem on page 1. You can also take a look at our lesson on writing algebraic expressions for some tips on translating written words into math.

Try completing this problem on your own. When you're done, move on to the next page to check your answer and see an explanation of the steps.

A single ticket to the fair costs $8. A family pass costs $25 more than half of that. How much does a family pass cost?

Here's another problem to do on your own. As with the last problem, you can find the answer and explanation to this one on the next page.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo. Between the two of them, they donated $280. How much money did Mo give?

Problem 1 Answer

Here's Problem 1:

A single ticket to the fair costs $8. A family pass costs $25 more than half that. How much does a family pass cost?

Answer: $29

Let's solve this problem step by step. We'll solve it the same way we solved the problem on page 1.

Step 1: Read through the problem carefully

The first in solving any word problem is to find out what question the problem is asking you to solve and identify the information that will help you solve it . Let's look at the problem again. The question is right there in plain sight:

So is the information we'll need to answer the question:

• A single ticket costs $8 .
• The family pass costs $25 more than half the price of the single ticket.

Step 2: Represent the unknown numbers with variables

The unknown number in this problem is the cost of the family pass . We'll represent it with the variable f .

Step 3: Translate the rest of the problem

Let's look at the problem again. This time, the important facts are highlighted.

A single ticket to the fair costs $8 . A family pass costs $25 more than half that . How much does a family pass cost?

In other words, we could say that the cost of a family pass equals half of $8, plus $25 . To turn this into a problem we can solve, we'll have to translate it into math. Here's how:

• First, replace the cost of a family pass with our variable f .

f equals half of $8 plus $25

• Next, take out the dollar signs and replace words like plus and equals with operators.

f = half of 8 + 25

• Finally, translate the rest of the problem. Half of can be written as 1/2 times , or 1/2 ⋅ :

f = 1/2 ⋅ 8 + 25

Step 4: Solve the problem

Now all we have to do is solve our problem. Like with any problem, we can solve this one by following the order of operations.

• f is already alone on the left side of the equation, so all we have to do is calculate the right side.
• First, multiply 1/2 by 8 . 1/2 ⋅ 8 is 4 .
• Next, add 4 and 25. 4 + 25 equals 29 .

That's it! f is equal to 29. In other words, the cost of a family pass is $29 .

Step 5: Check your work

Finally, let's check our work by working backward from our answer. In this case, we should be able to correctly calculate the cost of a single ticket by using the cost we calculated for the family pass. Let's look at the original problem again.

We calculated that a family pass costs $29. Our problem says the pass costs $25 more than half the cost of a single ticket. In other words, half the cost of a single ticket will be $25 less than $29.

• We could translate this into this equation, with s standing for the cost of a single ticket.

1/2s = 29 - 25

• Let's work on the right side first. 29 - 25 is 4 .
• To find the value of s , we have to get it alone on the left side of the equation. This means getting rid of 1/2 . To do this, we'll multiply each side by the inverse of 1/2: 2 .

According to our math, s = 8 . In other words, if the family pass costs $29, the single ticket will cost $8. Looking at our original problem, that's correct!

So now we're sure about the answer to our problem: The cost of a family pass is $29 .

Problem 2 Answer

Here's Problem 2:

Answer: $70

Let's go through this problem one step at a time.

Start by asking what question the problem is asking you to solve and identifying the information that will help you solve it . What's the question here?

To solve the problem, you'll have to find out how much money Mo gave to charity. All the important information you need is in the problem:

• The amount Flor donated is three times as much the amount Mo donated
• Flor and Mo's donations add up to $280 total

The unknown number we're trying to identify in this problem is Mo's donation . We'll represent it with the variable m .

Here's the problem again. This time, the important facts are highlighted.

Flor and Mo both donated money to the same charity. Flor gave three times as much as Mo . Between the two of them, they donated $280 . How much money did Mo give?

The important facts of the problem could also be expressed this way:

Mo's donation plus Flor's donation equals $280

Because we know that Flor's donation is three times as much as Mo's donation, we could go even further and say:

Mo's donation plus three times Mo's donation equals $280

We can translate this into a math problem in only a few steps. Here's how:

• Because we've already said we'll represent the amount of Mo's donation with the variable m , let's start by replacing Mo's donation with m .

m plus three times m equals $280

• Next, we can put in mathematical operators in place of certain words. We'll also take out the dollar sign.

m + three times m = 280

• Finally, let's write three times mathematically. Three times m can also be written as 3 ⋅ m , or just 3 m .

m + 3m = 280

It will only take a few steps to solve this problem.

• To get the correct answer, we'll have to get m alone on one side of the equation.
• To start, let's add m and 3 m . That's 4 m .
• We can get rid of the 4 next to the m by dividing both sides by 4. 4 m / 4 is m , and 280 / 4 is 70 .

We've got our answer: m = 70 . In other words, Mo donated $70 .

The answer to our problem is $70 , but we should check just to be sure. Let's look at our problem again.

If our answer is correct, $70 and three times $70 should add up to $280 .

• We can write our new equation like this:

70 + 3 ⋅ 70 = 280

• The order of operations calls for us to multiply first. 3 ⋅ 70 is 210.

70 + 210 = 280

• The last step is to add 70 and 210. 70 plus 210 equals 280 .

280 is the combined cost of the tickets in our original problem. Our answer is correct : Mo gave $70 to charity.

/en/algebra-topics/distance-word-problems/content/

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.20: Word Problems for Linear Equations

• Last updated
• Save as PDF
• Page ID 45640

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Word problems are important applications of linear equations. We start with examples of translating an English sentence or phrase into an algebraic expression.

Example 18.1

Translate the phrase into an algebraic expression:

a) Twice a variable is added to 4

Solution: We call the variable \(x .\) Twice the variable is \(2 x .\) Adding \(2 x\) to 4 gives:

\[4 + 2x\nonumber\]

b) Three times a number is subtracted from 7.

Solution: Three times a number is \(3 x .\) We need to subtract \(3 x\) from 7. This means:\

\[7-3 x\nonumber\]

c) 8 less than a number.

Solution: The number is denoted by \(x .8\) less than \(x\) mean, that we need to subtract 8 from it. We get:

\[x-8\nonumber\]

For example, 8 less than 10 is \(10-8=2\).

d) Subtract \(5 p^{2}-7 p+2\) from \(3 p^{2}+4 p\) and simplify.

Solution: We need to calculate \(3 p^{2}+4 p\) minus \(5 p^{2}-7 p+2:\)

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)\nonumber\]

Simplifying this expression gives:

\[\left(3 p^{2}+4 p\right)-\left(5 p^{2}-7 p+2\right)=3 p^{2}+4 p-5 p^{2}+7 p-2 =-2 p^{2}+11 p-2\nonumber\]

e) The amount of money given by \(x\) dimes and \(y\) quarters.

Solution: Each dime is worth 10 cents, so that this gives a total of \(10 x\) cents. Each quarter is worth 25 cents, so that this gives a total of \(25 y\) cents. Adding the two amounts gives a total of

\[10 x+25 y \text{ cents or } .10x + .25y \text{ dollars}\nonumber\]

Now we deal with word problems that directly describe an equation involving one variable, which we can then solve.

Example 18.2

Solve the following word problems:

a) Five times an unknown number is equal to 60. Find the number.

Solution: We translate the problem to algebra:

\[5x = 60\nonumber\]

We solve this for \(x\) :

\[x=\frac{60}{5}=12\nonumber\]

b) If 5 is subtracted from twice an unknown number, the difference is \(13 .\) Find the number.

Solution: Translating the problem into an algebraic equation gives:

\[2x − 5 = 13\nonumber\]

We solve this for \(x\). First, add 5 to both sides.

\[2x = 13 + 5, \text{ so that } 2x = 18\nonumber\]

Dividing by 2 gives \(x=\frac{18}{2}=9\).

c) A number subtracted from 9 is equal to 2 times the number. Find the number.

Solution: We translate the problem to algebra.

\[9 − x = 2x\nonumber\]

We solve this as follows. First, add \(x\) :

\[9 = 2x + x \text{ so that } 9 = 3x\nonumber\]

Then the answer is \(x=\frac{9}{3}=3\)

d) Multiply an unknown number by five is equal to adding twelve to the unknown number. Find the number.

Solution: We have the equation:

\[5x = x + 12.\nonumber\]

Subtracting \(x\) gives

\[4x = 12.\nonumber\]

Dividing both sides by 4 gives the answer: \(x=3\).

e) Adding nine to a number gives the same result as subtracting seven from three times the number. Find the number.

Solution: Adding 9 to a number is written as \(x+9,\) while subtracting 7 from three times the number is written as \(3 x-7\). We therefore get the equation:

\[x + 9 = 3x − 7.\nonumber\]

We solve for \(x\) by adding 7 on both sides of the equation:

\[x + 16 = 3x.\nonumber\]

Then we subtract \(x:\)

\[16 = 2x.\nonumber\]

After dividing by \(2,\) we obtain the answer \(x=8\)

The following word problems consider real world applications. They require to model a given situation in the form of an equation.

Example 18.3

a) Due to inflation, the price of a loaf of bread has increased by \(5 \%\). How much does the loaf of bread cost now, when its price was \(\$ 2.40\) last year?

Solution: We calculate the price increase as \(5 \% \cdot \$ 2.40 .\) We have

\[5 \% \cdot 2.40=0.05 \cdot 2.40=0.1200=0.12\nonumber\]

We must add the price increase to the old price.

\[2.40+0.12=2.52\nonumber\]

The new price is therefore \(\$ 2.52\).

b) To complete a job, three workers get paid at a rate of \(\$ 12\) per hour. If the total pay for the job was \(\$ 180,\) then how many hours did the three workers spend on the job?

Solution: We denote the number of hours by \(x\). Then the total price is calculated as the price per hour \((\$ 12)\) times the number of workers times the number of hours \((3) .\) We obtain the equation

\[12 \cdot 3 \cdot x=180\nonumber\]

Simplifying this yields

\[36 x=180\nonumber\]

Dividing by 36 gives

\[x=\frac{180}{36}=5\nonumber\]

Therefore, the three workers needed 5 hours for the job.

c) A farmer cuts a 300 foot fence into two pieces of different sizes. The longer piece should be four times as long as the shorter piece. How long are the two pieces?

\[x+4 x=300\nonumber\]

Combining the like terms on the left, we get

\[5 x=300\nonumber\]

Dividing by 5, we obtain that

\[x=\frac{300}{5}=60\nonumber\]

Therefore, the shorter piece has a length of 60 feet, while the longer piece has four times this length, that is \(4 \times 60\) feet \(=240\) feet.

d) If 4 blocks weigh 28 ounces, how many blocks weigh 70 ounces?

Solution: We denote the weight of a block by \(x .\) If 4 blocks weigh \(28,\) then a block weighs \(x=\frac{28}{4}=7\)

How many blocks weigh \(70 ?\) Well, we only need to find \(\frac{70}{7}=10 .\) So, the answer is \(10 .\)

Note You can solve this problem by setting up and solving the fractional equation \(\frac{28}{4}=\frac{70}{x}\). Solving such equations is addressed in chapter 24.

e) If a rectangle has a length that is three more than twice the width and the perimeter is 20 in, what are the dimensions of the rectangle?

Solution: We denote the width by \(x\). Then the length is \(2 x+3\). The perimeter is 20 in on one hand and \(2(\)length\()+2(\)width\()\) on the other. So we have

\[20=2 x+2(2 x+3)\nonumber\]

Distributing and collecting like terms give

\[20=6 x+6\nonumber\]

Subtracting 6 from both sides of the equation and then dividing both sides of the resulting equation by 6 gives:

\[20-6=6 x \Longrightarrow 14=6 x \Longrightarrow x=\frac{14}{6} \text { in }=\frac{7}{3} \text { in }=2 \frac{1}{3} \text { in. }\nonumber\]

f) If a circle has circumference 4in, what is its radius?

Solution: We know that \(C=2 \pi r\) where \(C\) is the circumference and \(r\) is the radius. So in this case

\[4=2 \pi r\nonumber\]

Dividing both sides by \(2 \pi\) gives

\[r=\frac{4}{2 \pi}=\frac{2}{\pi} \text { in } \approx 0.63 \mathrm{in}\nonumber\]

g) The perimeter of an equilateral triangle is 60 meters. How long is each side?

Solution: Let \(x\) equal the side of the triangle. Then the perimeter is, on the one hand, \(60,\) and on other hand \(3 x .\) So \(3 x=60\) and dividing both sides of the equation by 3 gives \(x=20\) meters.

h) If a gardener has \(\$ 600\) to spend on a fence which costs \(\$ 10\) per linear foot and the area to be fenced in is rectangular and should be twice as long as it is wide, what are the dimensions of the largest fenced in area?

Solution: The perimeter of a rectangle is \(P=2 L+2 W\). Let \(x\) be the width of the rectangle. Then the length is \(2 x .\) The perimeter is \(P=2(2 x)+2 x=6 x\). The largest perimeter is \(\$ 600 /(\$ 10 / f t)=60\) ft. So \(60=6 x\) and dividing both sides by 6 gives \(x=60 / 6=10\). So the dimensions are 10 feet by 20 feet.

i) A trapezoid has an area of 20.2 square inches with one base measuring 3.2 in and the height of 4 in. Find the length of the other base.

Solution: Let \(b\) be the length of the unknown base. The area of the trapezoid is on the one hand 20.2 square inches. On the other hand it is \(\frac{1}{2}(3.2+b) \cdot 4=\) \(6.4+2 b .\) So

\[20.2=6.4+2 b\nonumber\]

Multiplying both sides by 10 gives

\[202=64+20 b\nonumber\]

Subtracting 64 from both sides gives

\[b=\frac{138}{20}=\frac{69}{10}=6.9 \text { in }\nonumber\]

and dividing by 20 gives

Exit Problem

Write an equation and solve: A car uses 12 gallons of gas to travel 100 miles. How many gallons would be needed to travel 450 miles?

• April 14, 2020

Variable Expressions: Word Problems

Lesson Intro: Expressions with Variables

In this lesson, Juni Mathematics instructor Kadyn talks about variables and variable expressions – foundational concepts in pre-algebra. Variables are important to know for higher levels of math, and are even used similarly in other subjects like computer science!

Read Kadyn’s Intro to Variable Expressions lesson first to understand what variables are and how to use them in expressions. Then, use what you’ve learned with Kadyn’s word problems below to translate sentences and real-life problems into expressions with unknown variables. Learn to solve for unknowns, and tackle real-world applications.

Once you’ve checked your answers, you can also keep practicing using variables with Variable Expressions Drills and Warmup Problems .

Word Problems

Write out the following mathematical expression in full and then in simplified form: negative three times the difference of five times x and the absolute value of negative two minus three.

Ted is hosting a birthday party. If you take the number of friends he invited and multiply it by 4 and subtract it by 7, you get 53. How many people did Ted invite to his party?

Carmen wants to collect stamps and the store charges $3 for a pack of 12 stamps. How many stamps will Carmen have if she spent $36 on stamps? (disregard taxes)

Peter wants to build a rectangular fence around his yard. One side of the fence is 3m shorter than 4 times the other side. If the shorter side of the fence is 15m, what is the perimeter of the fence in meters?

Elliott and Gretchen are renting their own apartments in the city. Elliott has paid $10,000 in rent so far and Gretchen has paid $8,000. If both of them have been renting their own place for the same number of months and Gretchen’s monthly rate is $1,000, how much is Elliott’s monthly rent?

Find Solutions Below

-3 ⋅ (5x – |-2 -3|) = -3 ⋅ (5x – 5) = -15x + 15

Full form: -3 ⋅ (5x – |-2 -3|)

Simplified form: -15x + 15

Ted invited 15 people to his birthday party.

Let the number of people at Ted’s birthday party be n. Then n ⋅ 4 – 7 = 53 → n ⋅ 4 = 60. Then we know that n = 15.

Carmen has 144 stamps.

Let the number of stamps that Carmen has be s. Since she spent $36 on stamps and each pack of stamps cost $3, she then bought 36 3 = 12 packs. Since each pack comes in with 12 stamps, she has 12 ⋅ 12 = 144 stamps.

The perimeter of the fence is 144m.

Since the shorter side of the fence is 15m long, the longer side of the fence is 4 ⋅ 15 – 3 = 57m long. Then the perimeter of the fence is 15 + 15 + 57 + 57 = 144m.

Elliott’s monthly rent is $1,250.

Since Gretchen has paid $8,000 in rent and her monthly rent is $1,000, she has lived at her place for 8,000 1,000 = 8 months. Since Gretchen has lived at her place as long as Elliott has lived at his, we know that Elliott has lived at his place for 8 months as well. Then since Elliott has paid $10,000 in rent, his monthly rate is $10,000 8 = $1,250.

More Exercises on Variables

We hope you enjoyed Kadyn’s Word Problems with Variable Expressions! This lesson falls under our Pre-Algebra A course curriculum .

Continue practicing variable expressions with warmup problems and practice drills below. Or, review key terms and concepts with Kadyn’s Intro to Variables lesson.

• Intro to Variable Expressions: Definitions and Approaches
• Warmup Questions with Variable Expressions
• Variable Expressions Drills

Need help or want to keep learning?

To keep practicing or learning, please check out all of our math and coding tutorials on our Home Learning Resources page .

Need help? Looking up your questions is one of the best ways to learn! Another great way to learn is from an experienced math instructor. Read more about our online math courses or speak with a Juni Advisor by calling __(650) 263-4306__ or emailing [email protected]__.

Python Coding Classes for Kids: This Is How to Start

Block Coding for Kids: What Is It and Why Is It Effective?

Coding Projects for Kids: Fun Ways to Get Into Programming

Go further with juni.

Find your potential through our exclusive educational content, guides, and resources only available to Juni Subscribers.

Recent Posts

Looking for a juni course check out our course explorer.

EXPLORE ALL COURSES >>

Get fun activities sent straight to your inbox

Enjoyed this article? Become a Juni subscriber to get even more exclusive educational content, guides, and deals sent straight to your email inbox.

Investing & Entrepreneurship

Communications

Help with Schoolwork

All Courses

How It Works

Instructors

Student Projects

On Demand ACT & SAT Prep

Help Center & FAQ

Founders’ Story

Instructor Jobs

Our Policies

Subscribe to our newsletter

Learn about our latest events, resources, programs, and more!

By subscribing you agree with our Terms of Use & Privacy Policy .

2261 Market St #4242, San Francisco, CA 94114

[email protected]

Discover more from Juni Learning

Subscribe now to keep reading and get access to the full archive.

Type your email…

Continue reading

• Math for Kids
• Parenting Resources
• ELA for Kids
• Teaching Resources

How to Teach Number Formation in 5 Easy Steps

13 Best Resources for Math Videos for Kids: Math Made Fun

How to Teach Skip Counting to Kids in 9 Easy Steps

10 Best Math Intervention Strategies for Struggling Students

How to Teach Division to Kids in 11 Easy Steps

How to Cope With Test Anxiety in 12 Easy Ways

Developmental Milestones for 4 Year Olds: The Ultimate Guide

Simple & Stress-Free After School Schedule for Kids of All Ages

When Do Kids Start Preschool: Age & Readiness Skills

Kindergarten Readiness Checklist: A Guide for Parents

How to Teach Letter Formation to Kids in 9 Easy Steps

15 Best Literacy Activities for Preschoolers in 2024

12 Best Poems About Teachers Who Change Lives

6 Effective Ways to Improve Writing Skills

40 Four Letter Words That Start With A

60 Fun Animal Facts for Kids

12 Best Behavior Management Techniques for the Classroom

13 Best Online Teaching Tips for Teachers

How to Teach Kids to Write in 9 Easy Steps

13 Challenges for Teachers and How to Address Them

10 Best Strategies for Solving Math Word Problems

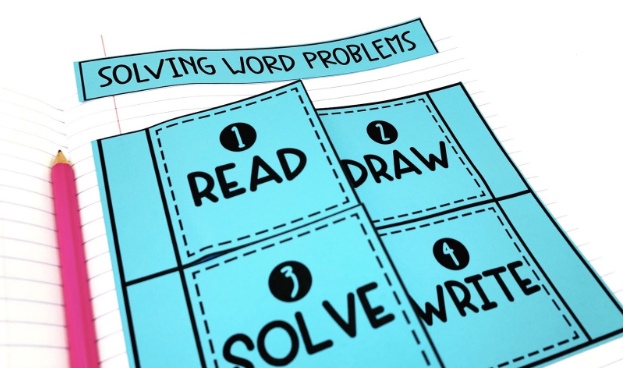
1. Understand the Problem by Paraphrasing

2. identify key information and variables, 3. translate words into mathematical symbols, 4. break down the problem into manageable parts, 5. draw diagrams or visual representations, 6. use estimation to predict answers, 7. apply logical reasoning for unknown variables, 8. leverage similar problems as templates, 9. check answers in the context of the problem, 10. reflect and learn from mistakes.

Have you ever observed the look of confusion on a student’s face when they encounter a math word problem ? It’s a common sight in classrooms worldwide, underscoring the need for effective strategies for solving math word problems . The main hurdle in solving math word problems is not just the math itself but understanding how to translate the words into mathematical equations that can be solved.

SplashLearn: Most Comprehensive Learning Program for PreK-5

SplashLearn inspires lifelong curiosity with its game-based PreK-5 learning program loved by over 40 million children. With over 4,000 fun games and activities, it’s the perfect balance of learning and play for your little one.

Generic advice like “read the problem carefully” or “practice more” often falls short in addressing students’ specific difficulties with word problems. Students need targeted math word problem strategies that address the root of their struggles head-on. 

A Guide on Steps to Solving Word Problems: 10 Strategies 

One of the first steps in tackling a math word problem is to make sure your students understand what the problem is asking. Encourage them to paraphrase the problem in their own words. This means they rewrite the problem using simpler language or break it down into more digestible parts. Paraphrasing helps students grasp the concept and focus on the problem’s core elements without getting lost in the complex wording.

Original Problem: “If a farmer has 15 apples and gives away 8, how many does he have left?”

Paraphrased: “A farmer had some apples. He gave some away. Now, how many apples does he have?”

This paraphrasing helps students identify the main action (giving away apples) and what they need to find out (how many apples are left).

Play these subtraction word problem games in the classroom for free:

Students often get overwhelmed by the details in word problems. Teach them to identify key information and variables essential for solving the problem. This includes numbers , operations ( addition , subtraction , multiplication , division ), and what the question is asking them to find. Highlighting or underlining can be very effective here. This visual differentiation can help students focus on what’s important, ignoring irrelevant details.

• Encourage students to underline numbers and circle keywords that indicate operations (like ‘total’ for addition and ‘left’ for subtraction).
• Teach them to write down what they’re solving for, such as “Find: Total apples left.”

Problem: “A classroom has 24 students. If 6 more students joined the class, how many students are there in total?”

Key Information:

• Original number of students (24)
• Students joined (6)
• Looking for the total number of students

Here are some fun addition word problems that your students can play for free:

The transition from the language of word problems to the language of mathematics is a critical skill. Teach your students to convert words into mathematical symbols and equations. This step is about recognizing keywords and phrases corresponding to mathematical operations and expressions .

Common Translations:

• “Total,” “sum,” “combined” → Addition (+)
• “Difference,” “less than,” “remain” → Subtraction (−)
• “Times,” “product of” → Multiplication (×)
• “Divided by,” “quotient of” → Division (÷)
• “Equals” → Equals sign (=)

Problem: “If one book costs $5, how much would 4 books cost?”

Translation: The word “costs” indicates a multiplication operation because we find the total cost of multiple items. Therefore, the equation is 4 × 5 = $20

Complex math word problems can often overwhelm students. Incorporating math strategies for problem solving, such as teaching them to break down the problem into smaller, more manageable parts, is a powerful approach to overcome this challenge. This means looking at the problem step by step rather than simultaneously trying to solve it. Breaking it down helps students focus on one aspect of the problem at a time, making finding the solution more straightforward.

Problem: “John has twice as many apples as Sarah. If Sarah has 5 apples, how many apples do they have together?”

Steps to Break Down the Problem:

Find out how many apples John has: Since John has twice as many apples as Sarah, and Sarah has 5, John has 5 × 2 = 10

Calculate the total number of apples: Add Sarah’s apples to John’s to find the total,  5 + 10 = 15

By splitting the problem into two parts, students can solve it without getting confused by all the details at once.

Explore these fun multiplication word problem games:

Diagrams and visual representations can be incredibly helpful for students, especially when dealing with spatial or quantity relationships in word problems. Encourage students to draw simple sketches or diagrams to represent the problem visually. This can include drawing bars for comparison, shapes for geometry problems, or even a simple distribution to better understand division or multiplication problems .

Problem: “A garden is 3 times as long as it is wide. If the width is 4 meters, how long is the garden?”

Visual Representation: Draw a rectangle and label the width as 4 meters. Then, sketch the length to represent it as three times the width visually, helping students see that the length is 4 × 3 = 12

Estimation is a valuable skill in solving math word problems, as it allows students to predict the answer’s ballpark figure before solving it precisely. Teaching students to use estimation can help them check their answers for reasonableness and avoid common mistakes.

Problem: “If a book costs $4.95 and you buy 3 books, approximately how much will you spend?”

Estimation Strategy: Round $4.95 to the nearest dollar ($5) and multiply by the number of books (3), so 5 × 3 = 15. Hence, the estimated total cost is about $15.

Estimation helps students understand whether their final answer is plausible, providing a quick way to check their work against a rough calculation.

Check out these fun estimation and prediction word problem worksheets that can be of great help:

When students encounter problems with unknown variables, it’s crucial to introduce them to logical reasoning. This strategy involves using the information in the problem to deduce the value of unknown variables logically. One of the most effective strategies for solving math word problems is working backward from the desired outcome. This means starting with the result and thinking about the steps leading to that result, which can be particularly useful in algebraic problems.

Problem: “A number added to three times itself equals 32. What is the number?”

Working Backward:

Let the unknown number be x.

The equation based on the problem is  x + 3x = 32

Solve for x by simplifying the equation to 4x=32, then dividing by 4 to find x=8.

By working backward, students can more easily connect the dots between the unknown variable and the information provided.

Practicing problems of similar structure can help students recognize patterns and apply known strategies to new situations. Encourage them to leverage similar problems as templates, analyzing how a solved problem’s strategy can apply to a new one. Creating a personal “problem bank”—a collection of solved problems—can be a valuable reference tool, helping students see the commonalities between different problems and reinforcing the strategies that work.

Suppose students have solved a problem about dividing a set of items among a group of people. In that case, they can use that strategy when encountering a similar problem, even if it’s about dividing money or sharing work equally.

It’s essential for students to learn the habit of checking their answers within the context of the problem to ensure their solutions make sense. This step involves going back to the original problem statement after solving it to verify that the answer fits logically with the given information. Providing a checklist for this process can help students systematically review their answers.

Checklist for Reviewing Answers:

• Re-read the problem: Ensure the question was understood correctly.
• Compare with the original problem: Does the answer make sense given the scenario?
• Use estimation: Does the precise answer align with an earlier estimation?
• Substitute back: If applicable, plug the answer into the problem to see if it works.

Problem: “If you divide 24 apples among 4 children, how many apples does each child get?”

After solving, students should check that they understood the problem (dividing apples equally).

Their answer (6 apples per child) fits logically with the number of apples and children.

Their estimation aligns with the actual calculation.

Substituting back 4×6=24 confirms the answer is correct.

Teaching students to apply logical reasoning, leverage solved problems as templates, and check their answers in context equips them with a robust toolkit for tackling math word problems efficiently and effectively.

One of the most effective ways for students to improve their problem-solving skills is by reflecting on their errors, especially with math word problems. Using word problem worksheets is one of the most effective strategies for solving word problems, and practicing word problems as it fosters a more thoughtful and reflective approach to problem-solving

These worksheets can provide a variety of problems that challenge students in different ways, allowing them to encounter and work through common pitfalls in a controlled setting. After completing a worksheet, students can review their answers, identify any mistakes, and then reflect on them in their mistake journal. This practice reinforces mathematical concepts and improves their math problem solving strategies over time.

3 Additional Tips for Enhancing Word Problem-Solving Skills

Before we dive into the importance of reflecting on mistakes, here are a few impactful tips to enhance students’ word problem-solving skills further:

1. Utilize Online Word Problem Games

Incorporate online games that focus on math word problems into your teaching. These interactive platforms make learning fun and engaging, allowing students to practice in a dynamic environment. Games can offer instant feedback and adaptive challenges, catering to individual learning speeds and styles.

Here are some word problem games that you can use for free:

2. Practice Regularly with Diverse Problems

Consistent practice with a wide range of word problems helps students become familiar with different questions and mathematical concepts. This exposure is crucial for building confidence and proficiency.

Start Practicing Word Problems with these Printable Word Problem Worksheets:

3. Encourage Group Work

Solving word problems in groups allows students to share strategies and learn from each other. A collaborative approach is one of the best strategies for solving math word problems that can unveil multiple methods for tackling the same problem, enriching students’ problem-solving toolkit.

Conclusion 

Mastering math word problems is a journey of small steps. Encourage your students to practice regularly, stay curious, and learn from their mistakes. These strategies for solving math word problems are stepping stones to turning challenges into achievements. Keep it simple, and watch your students grow their confidence and skills, one problem at a time.

Frequently Asked Questions (FAQs)

How can i help my students stay motivated when solving math word problems.

Encourage small victories and use engaging tools like online games to make practice fun and rewarding.

What's the best way to teach beginners word problems?

Begin with simple problems that integrate everyday scenarios to make the connection between math and real-life clear and relatable.

How often should students practice math word problems?

Regular, daily practice with various problems helps build confidence and problem-solving skills over time.

• Pre-Kindergarten
• Kindergarten

Most Popular

15 Best Report Card Comments Samples

117 Best Riddles for Kids (With Answers)

40 best good vibes quotes to brighten your day, recent posts.

What is World  Homeschooling & how To Start [Full Guide]

15 Best Movement Activities for Preschoolers in 2024

10 Best Online Homeschool Programs

Math & ela | prek to grade 5, kids see fun., you see real learning outcomes..

Watch your kids fall in love with math & reading through our scientifically designed curriculum.

Parents, try for free Teachers, use for free

• Games for Kids
• Worksheets for Kids
• Math Worksheets
• ELA Worksheets
• Math Vocabulary
• Number Games
• Addition Games
• Subtraction Games
• Multiplication Games
• Division Games
• Addition Worksheets
• Subtraction Worksheets
• Multiplication Worksheets
• Division Worksheets
• Times Tables Worksheets
• Reading Games
• Writing Games
• Phonics Games
• Sight Words Games
• Letter Tracing Games
• Reading Worksheets
• Writing Worksheets
• Phonics Worksheets
• Sight Words Worksheets
• Letter Tracing Worksheets
• Prime Number
• Order of Operations
• Long multiplication
• Place value
• Parallelogram
• SplashLearn Success Stories
• SplashLearn Apps
• [email protected]

© Copyright - SplashLearn

Make study-time fun with 14,000+ games & activities, 450+ lesson plans, and more—free forever.

Parents, Try for Free Teachers, Use for Free

Solving Word Questions

With LOTS of examples!

In Algebra we often have word questions like:

Example: Sam and Alex play tennis.

On the weekend Sam played 4 more games than Alex did, and together they played 12 games.

How many games did Alex play?

How do we solve them?

The trick is to break the solution into two parts:

Turn the English into Algebra.

Then use Algebra to solve.

Turning English into Algebra

To turn the English into Algebra it helps to:

• Read the whole thing first
• Do a sketch if possible
• Assign letters for the values
• Find or work out formulas

You should also write down what is actually being asked for , so you know where you are going and when you have arrived!

Also look for key words:

Thinking Clearly

Some wording can be tricky, making it hard to think "the right way around", such as:

Example: Sam has 2 dollars less than Alex. How do we write this as an equation?

• Let S = dollars Sam has
• Let A = dollars Alex has

Now ... is that: S − 2 = A

or should it be: S = A − 2

or should it be: S = 2 − A

The correct answer is S = A − 2

( S − 2 = A is a common mistake, as the question is written "Sam ... 2 less ... Alex")

Example: on our street there are twice as many dogs as cats. How do we write this as an equation?

• Let D = number of dogs
• Let C = number of cats

Now ... is that: 2D = C

or should it be: D = 2C

Think carefully now!

The correct answer is D = 2C

( 2D = C is a common mistake, as the question is written "twice ... dogs ... cats")

Let's start with a really simple example so we see how it's done:

Example: A rectangular garden is 12m by 5m, what is its area ?

Turn the English into Algebra:

• Use w for width of rectangle: w = 12m
• Use h for height of rectangle: h = 5m

Formula for Area of a Rectangle : A = w × h

We are being asked for the Area.

A = w × h = 12 × 5 = 60 m 2

The area is 60 square meters .

Now let's try the example from the top of the page:

Example: Sam and Alex play Tennis. On the weekend Sam played 4 more games than Alex did, and together they played 12 games. How many games did Alex play?

• Use S for how many games Sam played
• Use A for how many games Alex played

We know that Sam played 4 more games than Alex, so: S = A + 4

And we know that together they played 12 games: S + A = 12

We are being asked for how many games Alex played: A

Which means that Alex played 4 games of tennis.

Check: Sam played 4 more games than Alex, so Sam played 8 games. Together they played 8 + 4 = 12 games. Yes!

A slightly harder example:

Example: Alex and Sam also build tables. Together they make 10 tables in 12 days. Alex working alone can make 10 in 30 days. How long would it take Sam working alone to make 10 tables?

• Use a for Alex's work rate
• Use s for Sam's work rate

12 days of Alex and Sam is 10 tables, so: 12a + 12s = 10

30 days of Alex alone is also 10 tables: 30a = 10

We are being asked how long it would take Sam to make 10 tables.

30a = 10 , so Alex's rate (tables per day) is: a = 10/30 = 1/3

Which means that Sam's rate is half a table a day (faster than Alex!)

So 10 tables would take Sam just 20 days.

Should Sam be paid more I wonder?

And another "substitution" example:

Example: Jenna is training hard to qualify for the National Games. She has a regular weekly routine, training for five hours a day on some days and 3 hours a day on the other days. She trains altogether 27 hours in a seven day week. On how many days does she train for five hours?

• The number of "5 hour" days: d
• The number of "3 hour" days: e

We know there are seven days in the week, so: d + e = 7

And she trains 27 hours in a week, with d 5 hour days and e 3 hour days: 5d + 3e = 27

We are being asked for how many days she trains for 5 hours: d

The number of "5 hour" days is 3

Check : She trains for 5 hours on 3 days a week, so she must train for 3 hours a day on the other 4 days of the week.

3 × 5 hours = 15 hours, plus 4 × 3 hours = 12 hours gives a total of 27 hours

Some examples from Geometry:

Example: A circle has an area of 12 mm 2 , what is its radius?

• Use A for Area: A = 12 mm 2
• Use r for radius

And the formula for Area is: A = π r 2

We are being asked for the radius.

We need to rearrange the formula to find the area

Example: A cube has a volume of 125 mm 3 , what is its surface area?

Make a quick sketch:

• Use V for Volume
• Use A for Area
• Use s for side length of cube
• Volume of a cube: V = s 3
• Surface area of a cube: A = 6s 2

We are being asked for the surface area.

First work out s using the volume formula:

Now we can calculate surface area:

An example about Money:

Example: Joel works at the local pizza parlor. When he works overtime he earns 1¼ times the normal rate. One week Joel worked for 40 hours at the normal rate of pay and also worked 12 hours overtime. If Joel earned $660 altogether in that week, what is his normal rate of pay?

• Joel's normal rate of pay: $N per hour
• Joel works for 40 hours at $N per hour = $40N
• When Joel does overtime he earns 1¼ times the normal rate = $1.25N per hour
• Joel works for 12 hours at $1.25N per hour = $(12 × 1¼N) = $15N
• And together he earned $660, so:

$40N + $(12 × 1¼N) = $660

We are being asked for Joel's normal rate of pay $N.

So Joel’s normal rate of pay is $12 per hour

Joel’s normal rate of pay is $12 per hour, so his overtime rate is 1¼ × $12 per hour = $15 per hour. So his normal pay of 40 × $12 = $480, plus his overtime pay of 12 × $15 = $180 gives us a total of $660

More about Money, with these two examples involving Compound Interest

Example: Alex puts $2000 in the bank at an annual compound interest of 11%. How much will it be worth in 3 years?

This is the compound interest formula:

So we will use these letters:

• Present Value PV = $2,000
• Interest Rate (as a decimal): r = 0.11
• Number of Periods: n = 3
• Future Value (the value we want): FV

We are being asked for the Future Value: FV

Example: Roger deposited $1,000 into a savings account. The money earned interest compounded annually at the same rate. After nine years Roger's deposit has grown to $1,551.33 What was the annual rate of interest for the savings account?

The compound interest formula:

• Present Value PV = $1,000
• Interest Rate (the value we want): r
• Number of Periods: n = 9
• Future Value: FV = $1,551.33

We are being asked for the Interest Rate: r

So the annual rate of interest is 5%

Check : $1,000 × (1.05) 9 = $1,000 × 1.55133 = $1,551.33

And an example of a Ratio question:

Example: At the start of the year the ratio of boys to girls in a class is 2 : 1 But now, half a year later, four boys have left the class and there are two new girls. The ratio of boys to girls is now 4 : 3 How many students are there altogether now?

• Number of boys now: b
• Number of girls now: g

The current ratio is 4 : 3

Which can be rearranged to 3b = 4g

At the start of the year there was (b + 4) boys and (g − 2) girls, and the ratio was 2 : 1

b + 4 g − 2 = 2 1

Which can be rearranged to b + 4 = 2(g − 2)

We are being asked for how many students there are altogether now: b + g

There are 12 girls !

And 3b = 4g , so b = 4g/3 = 4 × 12 / 3 = 16 , so there are 16 boys

So there are now 12 girls and 16 boys in the class, making 28 students altogether .

There are now 16 boys and 12 girls, so the ratio of boys to girls is 16 : 12 = 4 : 3 At the start of the year there were 20 boys and 10 girls, so the ratio was 20 : 10 = 2 : 1

And now for some Quadratic Equations :

Example: The product of two consecutive even integers is 168. What are the integers?

Consecutive means one after the other. And they are even , so they could be 2 and 4, or 4 and 6, etc.

We will call the smaller integer n , and so the larger integer must be n+2

And we are told the product (what we get after multiplying) is 168, so we know:

n(n + 2) = 168

We are being asked for the integers

That is a Quadratic Equation , and there are many ways to solve it. Using the Quadratic Equation Solver we get −14 and 12.

Check −14: −14(−14 + 2) = (−14)×(−12) = 168 YES

Check 12: 12(12 + 2) = 12×14 = 168 YES

So there are two solutions: −14 and −12 is one, 12 and 14 is the other.

Note: we could have also tried "guess and check":

• We could try, say, n=10: 10(12) = 120 NO (too small)
• Next we could try n=12: 12(14) = 168 YES

But unless we remember that multiplying two negatives make a positive we might overlook the other solution of (−14)×(−12).

Example: You are an Architect. Your client wants a room twice as long as it is wide. They also want a 3m wide veranda along the long side. Your client has 56 square meters of beautiful marble tiles to cover the whole area. What should the length of the room be?

Let's first make a sketch so we get things right!:

• the length of the room: L
• the width of the room: W
• the total Area including veranda: A
• the width of the room is half its length: W = ½L
• the total area is the (room width + 3) times the length: A = (W+3) × L = 56

We are being asked for the length of the room: L

This is a quadratic equation , there are many ways to solve it, this time let's use factoring :

And so L = 8 or −14

There are two solutions to the quadratic equation, but only one of them is possible since the length of the room cannot be negative!

So the length of the room is 8 m

L = 8, so W = ½L = 4

So the area of the rectangle = (W+3) × L = 7 × 8 = 56

There we are ...

... I hope these examples will help you get the idea of how to handle word questions. Now how about some practice?

• Pre-Algebra Topics
• Algebra Topics
• Algebra Calculator
• Algebra Cheat Sheet
• Algebra Practice Test
• Algebra Readiness Test
• Algebra Formulas
• Want to Build Your Own Website?

Sign In / Register

REAL WORLD PROBLEMS: How to Write Equations Based on Algebra Word Problems

I know that you often sit in class and wonder, "Why am I forced to learn about equations, Algebra and variables?"

But... trust me, there are real situations where you will use your knowledge of Algebra and solving equations to solve a problem that is not school related. And... if you can't, you're going to wish that you remembered how.

It might be a time when you are trying to figure out how much you should get paid for a job, or even more important, if you were paid enough for a job that you've done. It could also be a time when you are trying to figure out if you were over charged for a bill.

This is important stuff - when it comes time to spend YOUR money - you are going to want to make sure that you are getting paid enough and not spending more than you have to.

Ok... let's put all this newly learned knowledge to work.

Click here if you need to review how to solve equations.

There are a few rules to remember when writing Algebra equations:

Writing Equations For Word Problems

• First, you want to identify the unknown, which is your variable. What are you trying to solve for? Identify the variable: Use the statement, Let x = _____. You can replace the x with whatever variable you are using.
• Look for key words that will help you write the equation. Highlight the key words and write an equation to match the problem.
• The following key words will help you write equations for Algebra word problems:

subtraction

Multiplication.

double (2x)

triple (3x)

quadruple (4x)

divided into

Let's look at an example of an algebra word problem.

Example 1: Algebra Word Problems

Linda was selling tickets for the school play.  She sold 10 more adult tickets than children tickets and she sold twice as many senior tickets as children tickets.

• Let x represent the number of children's tickets sold.
• Write an expression to represent the number of adult tickets sold.
• Write an expression to represent the number of senior tickets sold.
• Adult tickets cost $5, children's tickets cost $2, and senior tickets cost $3. Linda made $700. Write an equation to represent the total ticket sales.
• How many children's tickets were sold for the play? How many adult tickets were sold? How many senior tickets were sold?

As you can see, this problem is massive!  There are 5 questions to answer with many expressions to write. 

A few notes about this problem

1. In this problem, the variable was defined for you.  Let x represent the number of children’s tickets sold tells what x stands for in this problem.  If this had not been done for you, you might have written it like this:

        Let x = the number of children’s tickets sold

2. For the first expression, I knew that 10 more adult tickets were sold.  Since more means add, my expression was x +10 .  Since the direction asked for an expression, I don’t need an equal sign.  An equation is written with an equal sign and an expression is without an equal sign.  At this point we don’t know the total number of tickets.

3. For the second expression, I knew that my key words, twice as many meant two times as many.  So my expression was 2x .

4.  We know that to find the total price we have to multiply the price of each ticket by the number of tickets.  Take note that since x + 10 is the quantity of adult tickets, you must put it in parentheses!  So, when you multiply by the price of $5 you have to distribute the 5.

5.  Once I solve for x, I know the number of children’s tickets and I can take my expressions that I wrote for #1 and substitute 50 for x to figure out how many adult and senior tickets were sold.

Where Can You Find More Algebra Word Problems to Practice?

Word problems are the most difficult type of problem to solve in math. So, where can you find quality word problems WITH a detailed solution?

The Algebra Class E-course provides a lot of practice with solving word problems for every unit! The best part is.... if you have trouble with these types of problems, you can always find a step-by-step solution to guide you through the process!

Click here for more information.

The next example shows how to identify a constant within a word problem.

Example 2 - Identifying a Constant

A cell phone company charges a monthly rate of $12.95 and $0.25 a minute per call. The bill for m minutes is $21.20.

1. Write an equation that models this situation.

2. How many minutes were charged on this bill?

Notes For Example 2

• $12.95 is a monthly rate. Since this is a set fee for each month, I know that this is a constant. The rate does not change; therefore, it is not associated with a variable.
• $0.25 per minute per call requires a variable because the total amount will change based on the number of minutes. Therefore, we use the expression 0.25m
• You must solve the equation to determine the value for m, which is the number of minutes charged.

The last example is a word problem that requires an equation with variables on both sides.

Example 3 - Equations with Variables on Both Sides

You have $60 and your sister has $120. You are saving $7 per week and your sister is saving $5 per week. How long will it be before you and your sister have the same amount of money? Write an equation and solve.

Notes for Example 3

• $60 and $120 are constants because this is the amount of money that they each have to begin with. This amount does not change.
• $7 per week and $5 per week are rates. They key word "per" in this situation means to multiply.
• The key word "same" in this problem means that I am going to set my two expressions equal to each other.
• When we set the two expressions equal, we now have an equation with variables on both sides.
• After solving the equation, you find that x = 30, which means that after 30 weeks, you and your sister will have the same amount of money.

I'm hoping that these three examples will help you as you solve real world problems in Algebra!

• Solving Equations
• Algebra Word Problems

Need More Help With Your Algebra Studies?

Get access to hundreds of video examples and practice problems with your subscription! 

Click here for more information on our affordable subscription options.

Not ready to subscribe?  Register for our FREE Pre-Algebra Refresher course.

ALGEBRA CLASS E-COURSE MEMBERS

Click here for more information on our Algebra Class e-courses.

Need Help? Try This Online Calculator!

Affiliate Products...

On this site, I recommend only one product that I use and love and that is Mathway   If you make a purchase on this site, I may receive a small commission at no cost to you. 

Privacy Policy

Let Us Know How we are doing!

  send us a message to give us more detail!

Would you prefer to share this page with others by linking to it?

• Click on the HTML link code below.
• Copy and paste it, adding a note of your own, into your blog, a Web page, forums, a blog comment, your Facebook account, or anywhere that someone would find this page valuable.

Copyright © 2009-2020   |   Karin Hutchinson   |   ALL RIGHTS RESERVED.

One Variable Word Problems

Related Pages More Lessons for Grade 9 Math Worksheets

Videos, worksheets, solutions, and activities to help Algebra 1 students learn how to solve one variable word problems.

One variable Word Problem 1 Learn how to use algebra and one variable to define more than one unknown quantity, write an equation, solve it, and check it. Examples:

• Jamie earned 15 more points on her test than Paul earned. Their points add up to 143. How many points did each student earn?
• One number is 10 times another number and their difference is 63. Find the numbers.
• The difference between two numbers is 8. If the larger is subtracted from three times the smaller, the difference is 100. Find the numbers.

One variable Word Problem 2 Examples:

• Kim is two years older than three times Amy’s age. Their ages add up to 98. Find their ages.
• Nolan has 5 more quarters than dimes and 7 fewer nickels than dimes. He has 25 coins. How many of each coin does he have? How much money in dollars and cents is it worth?

One variable Word Problem 3 How to define two numbers that add up to a given number? Example: The sum of two numbers is 18. The sum of three times the smaller and twice the larger is 44. Find the numbers.

One variable Word Problem 4 Examples:

• The sum of two numbers is 15. One less than three times the smaller is equal to the larger. Find the numbers.
• The sum of two numbers is 2. The difference between eight and twice the smaller number is two less than four times the larger number. Find the numbers.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

• + ACCUPLACER Mathematics
• + ACT Mathematics
• + AFOQT Mathematics
• + ALEKS Tests
• + ASVAB Mathematics
• + ATI TEAS Math Tests
• + Common Core Math
• + DAT Math Tests
• + FSA Tests
• + FTCE Math
• + GED Mathematics
• + Georgia Milestones Assessment
• + GRE Quantitative Reasoning
• + HiSET Math Exam
• + HSPT Math
• + ISEE Mathematics
• + PARCC Tests
• + Praxis Math
• + PSAT Math Tests
• + PSSA Tests
• + SAT Math Tests
• + SBAC Tests
• + SIFT Math
• + SSAT Math Tests
• + STAAR Tests
• + TABE Tests
• + TASC Math
• + TSI Mathematics
• + ACT Math Worksheets
• + Accuplacer Math Worksheets
• + AFOQT Math Worksheets
• + ALEKS Math Worksheets
• + ASVAB Math Worksheets
• + ATI TEAS 6 Math Worksheets
• + FTCE General Math Worksheets
• + GED Math Worksheets
• + 3rd Grade Mathematics Worksheets
• + 4th Grade Mathematics Worksheets
• + 5th Grade Mathematics Worksheets
• + 6th Grade Math Worksheets
• + 7th Grade Mathematics Worksheets
• + 8th Grade Mathematics Worksheets
• + 9th Grade Math Worksheets
• + HiSET Math Worksheets
• + HSPT Math Worksheets
• + ISEE Middle-Level Math Worksheets
• + PERT Math Worksheets
• + Praxis Math Worksheets
• + PSAT Math Worksheets
• + SAT Math Worksheets
• + SIFT Math Worksheets
• + SSAT Middle Level Math Worksheets
• + 7th Grade STAAR Math Worksheets
• + 8th Grade STAAR Math Worksheets
• + THEA Math Worksheets
• + TABE Math Worksheets
• + TASC Math Worksheets
• + TSI Math Worksheets
• + AFOQT Math Course
• + ALEKS Math Course
• + ASVAB Math Course
• + ATI TEAS 6 Math Course
• + CHSPE Math Course
• + FTCE General Knowledge Course
• + GED Math Course
• + HiSET Math Course
• + HSPT Math Course
• + ISEE Upper Level Math Course
• + SHSAT Math Course
• + SSAT Upper-Level Math Course
• + PERT Math Course
• + Praxis Core Math Course
• + SIFT Math Course
• + 8th Grade STAAR Math Course
• + TABE Math Course
• + TASC Math Course
• + TSI Math Course
• + Number Properties Puzzles
• + Algebra Puzzles
• + Geometry Puzzles
• + Intelligent Math Puzzles
• + Ratio, Proportion & Percentages Puzzles
• + Other Math Puzzles

How to Solve Word Problems to Identify Independent and Dependent Variables

In this article, you will learn how to solve word problems to identify independent and dependent variables.

A step-by-step guide to solving word problems to identify independent and dependent variables

An Independent variable is one whose value does not depend on the other variable.

The dependent variable is the one whose value depends on the other variable.

To solve a word problem, first, you must list the information and then find the independent variable and dependent variable.

Here’s a step-by-step guide to solving word problems to identify independent and dependent variables:

Step 1: Read the problem carefully. Make sure you understand what is being asked in the problem. Look for keywords that will help you identify the variables, such as “depends on”, “varies with”, or “changes according to”.

Step 2: Identify the variables. Look for two variables in the problem – the independent variable and the dependent variable. The independent variable is the one that is being manipulated or changed in the problem, while the dependent variable is the one that is affected by the independent variable.

Step 3: Determine the relationship between the variables. Look for clues in the problem to help you determine the relationship between the variables. For example, if the problem says that “the cost of the ticket depends on the number of people attending”, then the independent variable is the number of people attending, and the dependent variable is the cost of the ticket. In this case, the more people attend, the higher the cost of the ticket.

Step 4: Write the equation. Once you have identified the independent and dependent variables and determined the relationship between them, you can write an equation to represent the problem. For example, if the problem states that “the temperature of the water varies with the amount of heat applied”, you can write the equation as Temperature = f(Heat).

Step 5: Solve the problem. Once you have the equation, you can use it to solve the problem. For example, if the problem asks you to find the temperature of the water when a certain amount of heat is applied, you can substitute the given value for heat in the equation and solve for temperature.

By following these steps, you can easily identify the independent and dependent variables in a word problem and solve it efficiently.

Solve Word Problems to Identify Independent and Dependent Variables – Example 1

Meg is making sandwiches to sell. The number of hotdogs she needs to use will affect how many the number of sandwiches she makes. s\(=\)The number of sandwiches she makes. h\(=\)The number of hotdogs she needs to use. Which of the variables is independent and which is dependent?

Find the dependent variable. Since the number of sandwiches depends on how many hotdogs to use, the number of sandwiches is the dependent variable. So, s is the dependent variable. Since the number of hotdogs, does not depend on how many sandwiches she makes; the hotdogs are the independent variable. So, h is the independent variable.

by: Effortless Math Team about 1 year ago (category: Articles )

Effortless Math Team

Related to this article, more math articles.

• Representing Percentage
• Strategies to Help Teachers Improve Student Retention
• Algebra 1 Fundamentals: A Guide for Students and Teachers
• FREE 3rd Grade Common Core Math Practice Test
• How to Solve Natural Logarithms Problems? (+FREE Worksheet!)
• 7th Grade OST Math Worksheets: FREE & Printable
• How is the CHSPE Test Scored?
• How to Find Discount, Tax, and Tip? (+FREE Worksheet!)
• How to Use Memory Tricks to Memorize Math Formulas?
• 3rd Grade FSA Math Worksheets: FREE & Printable

What people say about "How to Solve Word Problems to Identify Independent and Dependent Variables - Effortless Math: We Help Students Learn to LOVE Mathematics"?

No one replied yet.

Leave a Reply Cancel reply

You must be logged in to post a comment.

Mastering Grade 6 Math Word Problems The Ultimate Guide to Tackling 6th Grade Math Word Problems

Mastering grade 5 math word problems the ultimate guide to tackling 5th grade math word problems, mastering grade 7 math word problems the ultimate guide to tackling 7th grade math word problems, mastering grade 2 math word problems the ultimate guide to tackling 2nd grade math word problems, mastering grade 8 math word problems the ultimate guide to tackling 8th grade math word problems, mastering grade 4 math word problems the ultimate guide to tackling 4th grade math word problems, mastering grade 3 math word problems the ultimate guide to tackling 3rd grade math word problems.

• ATI TEAS 6 Math
• ISEE Upper Level Math
• SSAT Upper-Level Math
• Praxis Core Math
• 8th Grade STAAR Math

Limited time only!

Save Over 45 %

It was $89.99 now it is $49.99

Login and use all of our services.

Effortless Math services are waiting for you. login faster!

Register Fast!

Password will be generated automatically and sent to your email.

After registration you can change your password if you want.

• Math Worksheets
• Math Courses
• Math Topics
• Math Puzzles
• Math eBooks
• GED Math Books
• HiSET Math Books
• ACT Math Books
• ISEE Math Books
• ACCUPLACER Books
• Premium Membership
• Youtube Videos

Effortless Math provides unofficial test prep products for a variety of tests and exams. All trademarks are property of their respective trademark owners.

• Bulk Orders
• Refund Policy

Word Problems on Linear Equations

Worked-out word problems on linear equations with solutions explained step-by-step in different types of examples.

There are several problems which involve relations among known and unknown numbers and can be put in the form of equations. The equations are generally stated in words and it is for this reason we refer to these problems as word problems. With the help of equations in one variable, we have already practiced equations to solve some real life problems.

Steps involved in solving a linear equation word problem: ● Read the problem carefully and note what is given and what is required and what is given. ● Denote the unknown by the variables as x, y, ……. ● Translate the problem to the language of mathematics or mathematical statements. ● Form the linear equation in one variable using the conditions given in the problems. ● Solve the equation for the unknown. ● Verify to be sure whether the answer satisfies the conditions of the problem.

Step-by-step application of linear equations to solve practical word problems:

1. The sum of two numbers is 25. One of the numbers exceeds the other by 9. Find the numbers. 

Solution: Then the other number = x + 9 Let the number be x.  Sum of two numbers = 25 According to question, x + x + 9 = 25 ⇒ 2x + 9 = 25 ⇒ 2x = 25 - 9 (transposing 9 to the R.H.S changes to -9)  ⇒ 2x = 16 ⇒ 2x/2 = 16/2 (divide by 2 on both the sides)  ⇒ x = 8 Therefore, x + 9 = 8 + 9 = 17 Therefore, the two numbers are 8 and 17.

2.The difference between the two numbers is 48. The ratio of the two numbers is 7:3. What are the two numbers?  Solution:   Let the common ratio be x.  Let the common ratio be x.  Their difference = 48 According to the question,  7x - 3x = 48  ⇒ 4x = 48  ⇒ x = 48/4  ⇒ x = 12 Therefore, 7x = 7 × 12 = 84           3x = 3 × 12 = 36  Therefore, the two numbers are 84 and 36.

3. The length of a rectangle is twice its breadth. If the perimeter is 72 metre, find the length and breadth of the rectangle.  Solution: Let the breadth of the rectangle be x,  Then the length of the rectangle = 2x Perimeter of the rectangle = 72 Therefore, according to the question 2(x + 2x) = 72 ⇒ 2 × 3x = 72 ⇒ 6x = 72  ⇒ x = 72/6 ⇒ x = 12 We know, length of the rectangle = 2x                       = 2 × 12 = 24 Therefore, length of the rectangle is 24 m and breadth of the rectangle is 12 m.

4. Aaron is 5 years younger than Ron. Four years later, Ron will be twice as old as Aaron. Find their present ages. 

Solution: Let Ron’s present age be x.  Then Aaron’s present age = x - 5 After 4 years Ron’s age = x + 4, Aaron’s age x - 5 + 4.  According to the question;  Ron will be twice as old as Aaron.  Therefore, x + 4 = 2(x - 5 + 4)  ⇒ x + 4 = 2(x - 1)  ⇒ x + 4 = 2x - 2 ⇒ x + 4 = 2x - 2 ⇒ x - 2x = -2 - 4 ⇒ -x = -6 ⇒ x = 6 Therefore, Aaron’s present age = x - 5 = 6 - 5 = 1 Therefore, present age of Ron = 6 years and present age of Aaron = 1 year.

5. A number is divided into two parts, such that one part is 10 more than the other. If the two parts are in the ratio 5 : 3, find the number and the two parts.  Solution: Let one part of the number be x Then the other part of the number = x + 10 The ratio of the two numbers is 5 : 3 Therefore, (x + 10)/x = 5/3 ⇒ 3(x + 10) = 5x  ⇒ 3x + 30 = 5x ⇒ 30 = 5x - 3x ⇒ 30 = 2x  ⇒ x = 30/2  ⇒ x = 15 Therefore, x + 10 = 15 + 10 = 25 Therefore, the number = 25 + 15 = 40  The two parts are 15 and 25. 

More solved examples with detailed explanation on the word problems on linear equations.

6. Robert’s father is 4 times as old as Robert. After 5 years, father will be three times as old as Robert. Find their present ages.  Solution: Let Robert’s age be x years.  Then Robert’s father’s age = 4x After 5 years, Robert’s age = x + 5 Father’s age = 4x + 5 According to the question,  4x + 5 = 3(x + 5)  ⇒ 4x + 5 = 3x + 15  ⇒ 4x - 3x = 15 - 5  ⇒ x = 10 ⇒ 4x = 4 × 10 = 40  Robert’s present age is 10 years and that of his father’s age = 40 years.  

7. The sum of two consecutive multiples of 5 is 55. Find these multiples.  Solution: Let the first multiple of 5 be x.  Then the other multiple of 5 will be x + 5 and their sum = 55 Therefore, x + x + 5 = 55 ⇒ 2x + 5 = 55 ⇒ 2x = 55 - 5 ⇒ 2x = 50 ⇒ x = 50/2  ⇒ x = 25  Therefore, the multiples of 5, i.e., x + 5 = 25 + 5 = 30 Therefore, the two consecutive multiples of 5 whose sum is 55 are 25 and 30.  

8. The difference in the measures of two complementary angles is 12°. Find the measure of the angles.  Solution: Let the angle be x.  Complement of x = 90 - x Given their difference = 12° Therefore, (90 - x) - x = 12° ⇒ 90 - 2x = 12 ⇒ -2x = 12 - 90 ⇒ -2x = -78 ⇒ 2x/2 = 78/2 ⇒ x = 39 Therefore, 90 - x = 90 - 39 = 51  Therefore, the two complementary angles are 39° and 51°

9. The cost of two tables and three chairs is $705. If the table costs $40 more than the chair, find the cost of the table and the chair.  Solution: The table cost $ 40 more than the chair.  Let us assume the cost of the chair to be x.  Then the cost of the table = $ 40 + x The cost of 3 chairs = 3 × x = 3x and the cost of 2 tables 2(40 + x)  Total cost of 2 tables and 3 chairs = $705 Therefore, 2(40 + x) + 3x = 705 80 + 2x + 3x = 705 80 + 5x = 705 5x = 705 - 80 5x = 625/5 x = 125 and 40 + x = 40 + 125 = 165 Therefore, the cost of each chair is $125 and that of each table is $165. 

10. If 3/5 ᵗʰ of a number is 4 more than 1/2 the number, then what is the number?  Solution: Let the number be x, then 3/5 ᵗʰ of the number = 3x/5 Also, 1/2 of the number = x/2  According to the question,  3/5 ᵗʰ of the number is 4 more than 1/2 of the number.  ⇒ 3x/5 - x/2 = 4 ⇒ (6x - 5x)/10 = 4 ⇒ x/10 = 4 ⇒ x = 40 The required number is 40.  

Try to follow the methods of solving word problems on linear equations and then observe the detailed instruction on the application of equations to solve the problems.

●   Equations

What is an Equation?

What is a Linear Equation?

How to Solve Linear Equations?

Solving Linear Equations

Problems on Linear Equations in One Variable

Word Problems on Linear Equations in One Variable

Practice Test on Linear Equations

Practice Test on Word Problems on Linear Equations

●   Equations - Worksheets

Worksheet on Linear Equations

Worksheet on Word Problems on Linear Equation

7th Grade Math Problems   8th Grade Math Practice   From Word Problems on Linear Equations to HOME PAGE

Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.

New! Comments

• Preschool Activities
• Kindergarten Math
• 1st Grade Math
• 2nd Grade Math
• 3rd Grade Math
• 4th Grade Math
• 5th Grade Math
• 6th Grade Math
• 7th Grade Math
• 8th Grade Math
• 9th Grade Math
• 10th Grade Math
• 11 & 12 Grade Math
• Concepts of Sets
• Probability
• Boolean Algebra
• Math Coloring Pages
• Multiplication Table
• Cool Maths Games
• Math Flash Cards
• Online Math Quiz
• Math Puzzles
• Binary System
• Math Dictionary
• Conversion Chart
• Homework Sheets
• Math Problem Ans
• Free Math Answers
• Printable Math Sheet
• Funny Math Answers
• Employment Test
• Math Patterns
• Link Partners
• Privacy Policy

Recent Articles

Numbers | Notation | Numeration | Numeral | Estimation | Examples

May 12, 24 06:28 PM

Face Value and Place Value|Difference Between Place Value & Face Value

May 12, 24 06:23 PM

Patterns in Numbers | Patterns in Maths |Math Patterns|Series Patterns

May 12, 24 06:09 PM

Worksheet on Bar Graphs | Bar Graphs or Column Graphs | Graphing Bar

May 12, 24 04:59 PM

Worksheet on Pictographs | Picture Graph Worksheets | Pictograph Works

May 12, 24 04:31 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.

Reading & Math for K-5

• Kindergarten
• Learning numbers
• Comparing numbers
• Place Value
• Roman numerals
• Subtraction
• Multiplication
• Order of operations
• Drills & practice
• Measurement
• Factoring & prime factors
• Proportions
• Shape & geometry
• Data & graphing
• Word problems
• Children's stories
• Leveled Stories
• Context clues
• Cause & effect
• Compare & contrast
• Fact vs. fiction
• Fact vs. opinion
• Main idea & details
• Story elements
• Conclusions & inferences
• Sounds & phonics
• Words & vocabulary
• Reading comprehension
• Early writing
• Numbers & counting
• Simple math
• Social skills
• Other activities
• Dolch sight words
• Fry sight words
• Multiple meaning words
• Prefixes & suffixes
• Vocabulary cards
• Other parts of speech
• Punctuation
• Capitalization
• Narrative writing
• Opinion writing
• Informative writing
• Cursive alphabet
• Cursive letters
• Cursive letter joins
• Cursive words
• Cursive sentences
• Cursive passages
• Grammar & Writing

Breadcrumbs

• Word Problems

Download & Print From only $2.60

Word problems with variables

Variables and expressions.

These word problems involve expressions with variables . Students write expressions (using addition, subtraction, multiplication, division & fractions) which include an unknown represented by a variable.

These worksheets are available to members only.

Join K5 to save time, skip ads and access more content. Learn More

More word problem worksheets

Explore all of our math word problem worksheets , from kindergarten through grade 5.

What is K5?

K5 Learning offers free worksheets , flashcards  and inexpensive  workbooks  for kids in kindergarten to grade 5. Become a member  to access additional content and skip ads.

Our members helped us give away millions of worksheets last year.

We provide free educational materials to parents and teachers in over 100 countries. If you can, please consider purchasing a membership ($24/year) to support our efforts.

Members skip ads and access exclusive features.

Learn about member benefits

This content is available to members only.

• Forgot Password?