easy maths problem solving questions

Math Word Problems

Welcome to the math word problems worksheets page at Math-Drills.com! On this page, you will find Math word and story problems worksheets with single- and multi-step solutions on a variety of math topics including addition, multiplication, subtraction, division and other math topics. It is usually a good idea to ensure students already have a strategy or two in place to complete the math operations involved in a particular question. For example, students may need a way to figure out what 7 × 8 is or have previously memorized the answer before you give them a word problem that involves finding the answer to 7 × 8.

There are a number of strategies used in solving math word problems; if you don't have a favorite, try the Math-Drills.com problem-solving strategy:

• Question : Understand what the question is asking. What operation or operations do you need to use to solve this question? Ask for help to understand the question if you can't do it on your own.
• Estimate : Use an estimation strategy, so you can check your answer for reasonableness in the evaluate step. Try underestimating and overestimating, so you know what range the answer is supposed to be in. Be flexible in rounding numbers if it will make your estimate easier.
• Strategize : Choose a strategy to solve the problem. Will you use mental math, manipulatives, or pencil and paper? Use a strategy that works for you. Save the calculator until the evaluate stage.
• Calculate : Use your strategy to solve the problem.
• Evaluate : Compare your answer to your estimate. If you under and overestimated, is the answer in the correct range. If you rounded up or down, does the answer make sense (e.g. is it a little less or a little more than the estimate). Also check with a calculator.

Most Popular Math Word Problems this Week

Arithmetic Word Problems

• Addition Word Problems One-Step Addition Word Problems Using Single-Digit Numbers One-Step Addition Word Problems Using Two-Digit Numbers
• Subtraction Word Problems Subtraction Facts Word Problems With Differences from 5 to 12
• Multiplication Word Problems One-Step Multiplication Word Problems up to 10 × 10
• Division Word Problems Division Facts Word Problems with Quotients from 5 to 12
• Multi-Step Word Problems Easy Multi-Step Word Problems

Copyright © 2005-2024 Math-Drills.com You may use the math worksheets on this website according to our Terms of Use to help students learn math.

• Pre-algebra lessons
• Pre-algebra word problems
• Algebra lessons

Algebra word problems

• Algebra proofs
• Advanced algebra
• Geometry lessons
• Geometry word problems
• Geometry proofs
• Trigonometry lessons
• Consumer math
• Baseball math
• Math for nurses
• Statistics made easy
• High school physics
• Basic mathematics store
• SAT Math Prep
• Math skills by grade level
• Ask an expert
• Other websites
• K-12 worksheets
• Worksheets generator
• Algebra worksheets
• Geometry worksheets
• Free math problem solver
• Pre-algebra calculators
• Algebra Calculators
• Geometry Calculators
• Math puzzles
• Math tricks
• Member login

Basic math word problems

You encounter and solve basic math word problems on a daily basis without thinking about it. Knowing how to tackle and solve word problems is an important skill in school. You may find it useful to review some math problem solving strategies .

Whole number word problems

Fractions word problems, ratio and proportion word problems .

Ratio word problems Six carefully selected ratio word problems with solutions to help you master ratios. Proportion word problems Four carefully selected proportion word problems with solutions.

Convert square feet to acres See how you can use proportion to convert square feet to acres

Percentage word problems

Average word problems.

Average word problems Word problems about finding the average from easy to challenging

Comparison word problems

Comparison word problems A variety of comparison word problems from easy to challenging

Venn diagram word problems

Venn diagram word problems A variety of word problems from easy to challenging

Have A Great Basic Math Word Problem?

Share it here with a very detailed solution!

Enter Your Title

Add a Picture/Graphic Caption (optional)  

Click here to upload more images (optional)

Author Information (optional)

To receive credit as the author, enter your information below.

Submit Your Contribution

• Check box to agree to these   submission guidelines .
• I am at least 16 years of age.
• I understand and accept the privacy policy .
• I understand that you will display my submission on your website.

(You can preview and edit on the next page)

What Other Visitors Have Said

Click below to see contributions from other visitors to this page...

Click here to write your own.

Recent Articles

How to divide any number by 5 in 2 seconds.

Feb 28, 24 11:07 AM

Math Trick to Square Numbers from 50 to 59

Feb 23, 24 04:46 AM

Sum of Consecutive Odd Numbers

Feb 22, 24 10:07 AM

100 Tough Algebra Word Problems. If you can solve these problems with no help, you must be a genius!

 Recommended

About me :: Privacy policy :: Disclaimer :: Donate   Careers in mathematics  

Copyright © 2008-2021. Basic-mathematics.com. All right reserved

MathPapa Practice

MathPapa Practice has practice problems to help you learn algebra.

Basic Arithmetic

Subtraction, multiplication, basic arithmetic review, multi-digit arithmetic, addition (2-digit), subtraction (2-digit), multiplication (2-digit by 1-digit), division (2-digit answer), multiplication (2-digit by 2-digit), multi-digit division, negative numbers, addition: negative numbers, subtraction: negative numbers, multiplication: negative numbers, division: negative numbers, order of operations, order of operations 1, basic equations, equations: fill in the blank 1, equations: fill in the blank 2, equations: fill in the blank 3 (order of operations), fractions of measurements, fractions of measurements 2, adding fractions, subtracting fractions, adding fractions: fill in the blank, multiplication: fractions 1, multiplication: fractions 2, division: fractions 1, division: fractions 2, division: fractions 3, addition (decimals), subtraction (decimals), multiplication 2 (example problem: 3.5*8), multiplication 3 (example problem: 0.3*80), division (decimals), division (decimals 2), percentages, percentages 1, percentages 2, chain reaction, balance arithmetic, number balance, basic balance 1, basic balance 2, basic balance 3, basic balance 4, basic balance 5, basic algebra, basic algebra 1, basic algebra 2, basic algebra 3, basic algebra 4, basic algebra 5, algebra: basic fractions 1, algebra: basic fractions 2, algebra: basic fractions 3, algebra: basic fractions 4, algebra: basic fractions 5.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

What can QuickMath do?

QuickMath will automatically answer the most common problems in algebra, equations and calculus faced by high-school and college students.

• The algebra section allows you to expand, factor or simplify virtually any expression you choose. It also has commands for splitting fractions into partial fractions, combining several fractions into one and cancelling common factors within a fraction.
• The equations section lets you solve an equation or system of equations. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require.
• The inequalities section lets you solve an inequality or a system of inequalities for a single variable. You can also plot inequalities in two variables.
• The calculus section will carry out differentiation as well as definite and indefinite integration.
• The matrices section contains commands for the arithmetic manipulation of matrices.
• The graphs section contains commands for plotting equations and inequalities.
• The numbers section has a percentages command for explaining the most common types of percentage problems and a section for dealing with scientific notation.

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Or search by topic

Number and algebra

• The Number System and Place Value
• Calculations and Numerical Methods
• Fractions, Decimals, Percentages, Ratio and Proportion
• Properties of Numbers
• Patterns, Sequences and Structure
• Algebraic expressions, equations and formulae
• Coordinates, Functions and Graphs

Geometry and measure

• Angles, Polygons, and Geometrical Proof
• 3D Geometry, Shape and Space
• Measuring and calculating with units
• Transformations and constructions
• Pythagoras and Trigonometry
• Vectors and Matrices

Probability and statistics

• Handling, Processing and Representing Data
• Probability

Working mathematically

• Thinking mathematically
• Mathematical mindsets
• Cross-curricular contexts
• Physical and digital manipulatives

For younger learners

• Early Years Foundation Stage

Advanced mathematics

• Decision Mathematics and Combinatorics
• Advanced Probability and Statistics

Short problems for Starters, Homework and Assessment

Number - Short Problems

A collection of short Stage 3 and 4 problems on number.

Algebra - Short Problems

A collection of short Stage 3 and 4 problems on algebra.

Geometry and Measure - Short Problems

A collection of short Stage 3 and 4 problems on geometry and measure.

Handling Data - Short Problems

A collection of short Stage 3 and 4 problems on handling data.

Thinking Mathematically - Short Problems

A collection of short problems which require students to think mathematically.

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Unit 2: Solving equations & inequalities

About this unit.

There are lots of strategies we can use to solve equations. Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions.

Linear equations with variables on both sides

• Why we do the same thing to both sides: Variable on both sides (Opens a modal)
• Intro to equations with variables on both sides (Opens a modal)
• Equations with variables on both sides: 20-7x=6x-6 (Opens a modal)
• Equation with variables on both sides: fractions (Opens a modal)
• Equation with the variable in the denominator (Opens a modal)
• Equations with variables on both sides Get 3 of 4 questions to level up!
• Equations with variables on both sides: decimals & fractions Get 3 of 4 questions to level up!

Linear equations with parentheses

• Equations with parentheses (Opens a modal)
• Reasoning with linear equations (Opens a modal)
• Multi-step equations review (Opens a modal)
• Equations with parentheses Get 3 of 4 questions to level up!
• Equations with parentheses: decimals & fractions Get 3 of 4 questions to level up!
• Reasoning with linear equations Get 3 of 4 questions to level up!

Analyzing the number of solutions to linear equations

• Number of solutions to equations (Opens a modal)
• Worked example: number of solutions to equations (Opens a modal)
• Creating an equation with no solutions (Opens a modal)
• Creating an equation with infinitely many solutions (Opens a modal)
• Number of solutions to equations Get 3 of 4 questions to level up!
• Number of solutions to equations challenge Get 3 of 4 questions to level up!

Linear equations with unknown coefficients

• Linear equations with unknown coefficients (Opens a modal)
• Why is algebra important to learn? (Opens a modal)
• Linear equations with unknown coefficients Get 3 of 4 questions to level up!

Multi-step inequalities

• Inequalities with variables on both sides (Opens a modal)
• Inequalities with variables on both sides (with parentheses) (Opens a modal)
• Multi-step inequalities (Opens a modal)
• Using inequalities to solve problems (Opens a modal)
• Multi-step linear inequalities Get 3 of 4 questions to level up!
• Using inequalities to solve problems Get 3 of 4 questions to level up!

Compound inequalities

• Compound inequalities: OR (Opens a modal)
• Compound inequalities: AND (Opens a modal)
• A compound inequality with no solution (Opens a modal)
• Double inequalities (Opens a modal)
• Compound inequalities examples (Opens a modal)
• Compound inequalities review (Opens a modal)
• Solving equations & inequalities: FAQ (Opens a modal)
• Compound inequalities Get 3 of 4 questions to level up!

Get step-by-step solutions to your math problems

Try Math Solver

Get step-by-step explanations

Graph your math problems

Practice, practice, practice

Get math help in your language

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators

Simple Algebra Problems – Easy Exercises with Solutions for Beginners

JUMP TO TOPIC

Understanding Algebraic Expressions

Breaking down algebra problems, solving algebraic equations, tackling algebra word problems, types of algebraic equations, algebra for different grades.

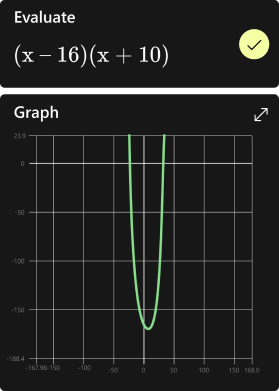
For instance, solving the equation (3x = 7) for (x) helps us understand how to isolate the variable to find its value.

I always find it fascinating how algebra serves as the foundation for more advanced topics in mathematics and science. Starting with basic problems such as ( $(x-1)^2 = [4\sqrt{(x-4)}]^2$ ) allows us to grasp key concepts and build the skills necessary for tackling more complex challenges.

So whether you’re refreshing your algebra skills or just beginning to explore this mathematical language, let’s dive into some examples and solutions to demystify the subject. Trust me, with a bit of practice, you’ll see algebra not just as a series of problems, but as a powerful tool that helps us solve everyday puzzles.

Simple Algebra Problems and Strategies

When I approach simple algebra problems, one of the first things I do is identify the variable.

The variable is like a placeholder for a number that I’m trying to find—a mystery I’m keen to solve. Typically represented by letters like ( x ) or ( y ), variables allow me to translate real-world situations into algebraic expressions and equations.

An algebraic expression is a mathematical phrase that can contain ordinary numbers, variables (like ( x ) or ( y )), and operators (like add, subtract, multiply, and divide). For example, ( 4x + 7 ) is an algebraic expression where ( x ) is the variable and the numbers ( 4 ) and ( 7 ) are terms. It’s important to manipulate these properly to maintain the equation’s balance.

Solving algebra problems often starts with simplifying expressions. Here’s a simple method to follow:

• Combine like terms : Terms that have the same variable can be combined. For instance, ( 3x + 4x = 7x ).
• Isolate the variable : Move the variable to one side of the equation. If the equation is ( 2x + 5 = 13 ), my job is to get ( x ) by itself by subtracting ( 5 ) from both sides, giving me ( 2x = 8 ).

With algebraic equations, the goal is to solve for the variable by performing the same operation on both sides. Here’s a table with an example:

Algebra word problems require translating sentences into equations. If a word problem says “I have six less than twice the number of apples than Bob,” and Bob has ( b ) apples, then I’d write the expression as ( 2b – 6 ).

Understanding these strategies helps me tackle basic algebra problems efficiently. Remember, practice makes perfect, and each problem is an opportunity to improve.

In algebra, we encounter a variety of equation types and each serves a unique role in problem-solving. Here, I’ll brief you about some typical forms.

Linear Equations : These are the simplest form, where the highest power of the variable is one. They take the general form ( ax + b = 0 ), where ( a ) and ( b ) are constants, and ( x ) is the variable. For example, ( 2x + 3 = 0 ) is a linear equation.

Polynomial Equations : Unlike for linear equations, polynomial equations can have variables raised to higher powers. The general form of a polynomial equation is ( $a_nx^n + a_{n-1}x^{n-1} + … + a_2x^2 + a_1x + a_0 = 0$ ). In this equation, ( n ) is the highest power, and ( $a_n$ ), ( $a_{n-1} $), …, ( $a_0$ ) represent the coefficients which can be any real number.

• Binomial Equations : They are a specific type of polynomial where there are exactly two terms. Like ($ x^2 – 4 $), which is also the difference of squares, a common format encountered in factoring.

To understand how equations can be solved by factoring, consider the quadratic equation ( $x^2$ – 5x + 6 = 0 ). I can factor this into ( (x-2)(x-3) = 0 ), which allows me to find the roots of the equation.

Here’s how some equations look when classified by degree:

Remember, identification and proper handling of these equations are essential in algebra as they form the basis for complex problem-solving.

In my experience with algebra, I’ve found that the journey begins as early as the 6th grade, where students get their first taste of this fascinating subject with the introduction of variables representing an unknown quantity.

I’ve created worksheets and activities aimed specifically at making this early transition engaging and educational.

6th Grade :

Moving forward, the complexity of algebraic problems increases:

7th and 8th Grades :

• Mastery of negative numbers: students practice operations like ( -3 – 4 ) or ( -5 $\times$ 2 ).
• Exploring the rules of basic arithmetic operations with negative numbers.
• Worksheets often contain numeric and literal expressions that help solidify their concepts.

Advanced topics like linear algebra are typically reserved for higher education. However, the solid foundation set in these early grades is crucial. I’ve developed materials to encourage students to understand and enjoy algebra’s logic and structure.

Remember, algebra is a tool that helps us quantify and solve problems, both numerical and abstract. My goal is to make learning these concepts, from numbers to numeric operations, as accessible as possible, while always maintaining a friendly approach to education.

I’ve walked through various simple algebra problems to help establish a foundational understanding of algebraic concepts. Through practice, you’ll find that these problems become more intuitive, allowing you to tackle more complex equations with confidence.

Remember, the key steps in solving any algebra problem include:

• Identifying variables and what they represent.
• Setting up the equation that reflects the problem statement.
• Applying algebraic rules such as the distributive property ($a(b + c) = ab + ac$), combining like terms, and inverse operations.
• Checking your solutions by substituting them back into the original equations to ensure they work.

As you continue to engage with algebra, consistently revisiting these steps will deepen your understanding and increase your proficiency. Don’t get discouraged by mistakes; they’re an important part of the learning process.

I hope that the straightforward problems I’ve presented have made algebra feel more manageable and a little less daunting. Happy solving!

• Pre Calculus
• Probability
• Sets & Set Theory
• Trigonometry

Mastery-Aligned Maths Tutoring

“The best thing has been the increase in confidence and tutors being there to deal with any misunderstandings straight away."

FREE daily maths challenges

A new KS2 maths challenge every day. Perfect as lesson starters - no prep required!

30 Problem Solving Maths Questions And Answers For GCSE

Martin Noon

Problem solving maths questions can be challenging for GCSE students as there is no ‘one size fits all’ approach. In this article, we’ve compiled tips for problem solving, example questions, solutions and problem solving strategies for GCSE students. 

Since the current GCSE specification began, there have been many maths problem solving exam questions which take elements of different areas of maths and combine them to form new maths problems which haven’t been seen before. 

While learners can be taught to approach simply structured problems by following a process, questions often require students to make sense of lots of new information before they even move on to trying to solve the problem. This is where many learners get stuck.

How to teach problem solving

6 tips to tackling problem solving maths questions, 10 problem solving maths questions (foundation tier), 10 problem solving maths questions (foundation & higher tier crossover), 10 problem solving maths questions (higher tier).

In the Ofsted maths review , published in May 2021, Ofsted set out their findings from the research literature regarding the sort of curriculum and teaching that best supports all pupils to make good progress in maths throughout their time in school.

Regarding the teaching of problem solving skills, these were their recommendations:

• Teachers could use a curricular approach that better engineers success in problem-solving by teaching the useful combinations of facts and methods, how to recognise the problem types and the deep structures that these strategies pair to.
• Strategies for problem-solving should be topic specific and can therefore be planned into the sequence of lessons as part of the wider curriculum. Pupils who are already confident with the foundational skills may benefit from a more generalised process involving identifying relationships and weighing up features of the problem to process the information. 
• Worked examples, careful questioning and constructing visual representations can help pupils to convert information embedded in a problem into mathematical notation.
• Open-ended problem solving tasks do not necessarily mean that the activity is the ‘ideal means of acquiring proficiency’. While enjoyable, open ended problem-solving activities may not necessarily lead to improved results.  

Are you a KS2 teacher needing more support teaching reasoning, problem solving & planning for depth ? See this article for FREE downloadable CPD

There is no ‘one size fits all’ approach to successfully tackling problem solving maths questions however, here are 6 general tips for students facing a problem solving question:

• Read the whole question, underline important mathematical words, phrases or values.
• Annotate any diagrams, graphs or charts with any missing information that is easy to fill in.
• Think of what a sensible answer may look like. E.g. Will the angle be acute or obtuse? Is £30,000 likely to be the price of a coat?
• Tick off information as you use it.
• Draw extra diagrams if needed.
• Look at the final sentence of the question. Make sure you refer back to that at the end to ensure you have answered the question fully.

There are many online sources of mathematical puzzles and questions that can help learners improve their problem-solving skills. Websites such as NRICH and our blog on SSDD problems have some great examples of KS2, KS3 and KS4 mathematical problems.

Read more: KS2 problem solving and KS3 maths problem solving

In this article, we’ve focussed on GCSE questions and compiled 30 problem solving maths questions and solutions suitable for Foundation and Higher tier students. Additionally, we have provided problem solving strategies to support your students for some questions to encourage critical mathematical thinking . For the full set of questions, solutions and strategies in a printable format, please download our 30 Problem Solving Maths Questions, Solutions & Strategies.

30 Problem Solving Maths Questions, Solutions & Strategies

Help your students prepare for their maths GCSE with these free problem solving maths questions, solutions and strategies

These first 10 questions and solutions are similar to Foundation questions. For the first three, we’ve provided some additional strategies.

In our downloadable resource, you can find strategies for all 10 Foundation questions .

1) L-shape perimeter 

Here is a shape:

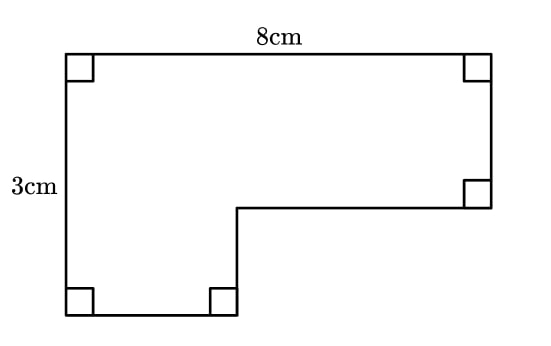
Sarah says, “There is not enough information to find the perimeter.”

Is she correct? What about finding the area?

• Try adding more information – giving some missing sides measurements that are valid. 
• Change these measurements to see if the answer changes.
• Imagine walking around the shape if the edges were paths. Could any of those paths be moved to another position but still give the same total distance?

The perimeter of the shape does not depend on the lengths of the unlabelled edges.

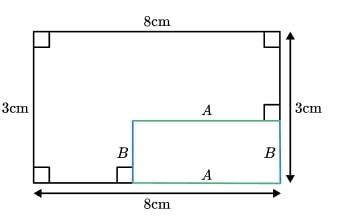
Edge A and edge B can be moved to form a rectangle, meaning the perimeter will be 22 cm. Therefore, Sarah is wrong.

The area, however, will depend on those missing side length measurements, so we would need more information to be able to calculate it.

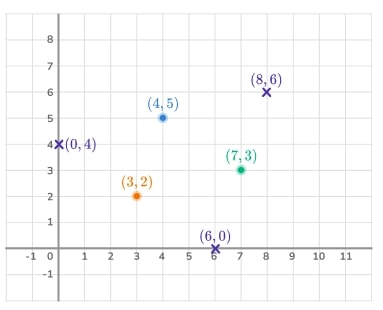
2) Find the missing point

Here is a coordinate grid with three points plotted. A fourth point is to be plotted to form a parallelogram. Find all possible coordinates of the fourth point.

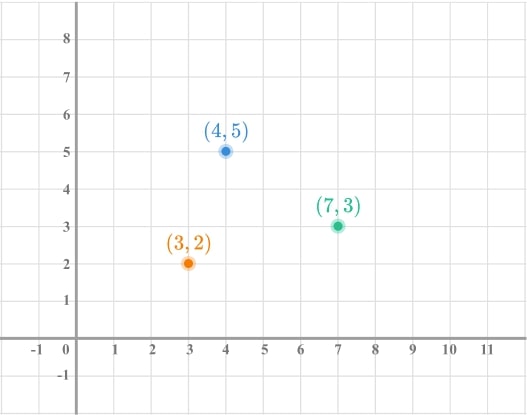
• What are the properties of a parallelogram?
• Can we count squares to see how we can get from one vertex of the parallelogram to another? Can we use this to find the fourth vertex?

There are 3 possible positions.

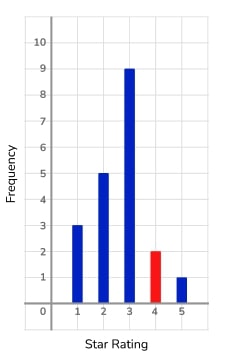
3) That rating was a bit mean!

The vertical line graph shows the ratings a product received on an online shopping website. The vertical line for 4 stars is missing.

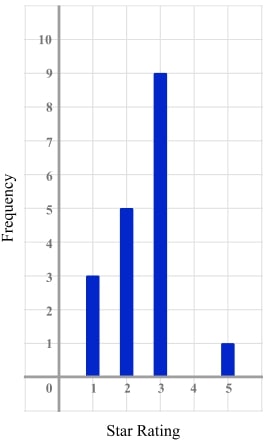
If the mean rating is 2.65, use the information to complete the vertical line graph.

Strategies 

• Can the information be put into a different format, either a list or a table?
• Would it help to give the missing frequency an algebraic label, x ?
• If we had the data in a frequency table, how would we calculate the mean?
• Is there an equation we could form?

Letting the frequency of 4 star ratings be x , we can form the equation \frac{45+4x}{18+x} =2.65

Giving x=2 

4) Changing angles

The diagram shows two angles around a point. The sum of the two angles around a point is 360°.

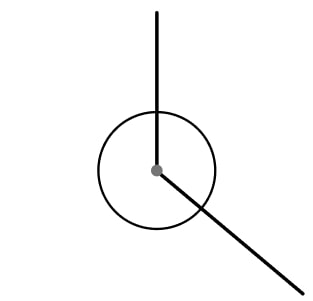
Peter says “If we increase the small angle by 10% and decrease the reflex angle by 10%, they will still add to 360°.”

Explain why Peter might be wrong.

Are there two angles where he would be correct?

Peter is wrong, for example, if the two angles are 40° and 320°, increasing 40° by 10% gives 44°, decreasing 320° by 10% gives 288°. These sum to 332°.

10% of the larger angle will be more than 10% of the smaller angle so the sum will only ever be 360° if the two original angles are the same, therefore, 180°.

5) Base and power

The integers 1, 2, 3, 4, 5, 6, 7, 8 and 9 can be used to fill in the boxes. 

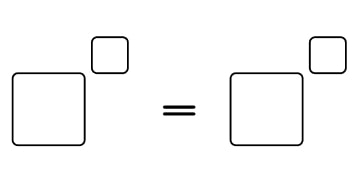
How many different solutions can be found so that no digit is used more than once?

There are 8 solutions.

6) Just an average problem 

Place six single digit numbers into the boxes to satisfy the rules.

The mean in maths is 5  \frac{1}{3}

The median is 5

The mode is 3.

How many different solutions are possible?

There are 4 solutions.

2, 3, 3, 7, 8, 9

3, 3, 4, 6, 7, 9

3, 3, 3, 7, 7, 9

3, 3, 3, 7, 8, 8

7) Square and rectangle  

The square has an area of 81 cm 2 . The rectangle has the same perimeter as the square.

Its length and width are in the ratio 2:1.

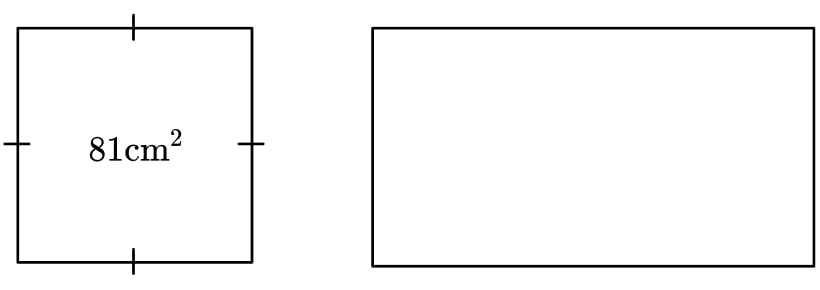
Find the area of the rectangle.

The sides of the square are 9 cm giving a perimeter of 36 cm. 

We can then either form an equation using a length 2x and width x . 

Or, we could use the fact that the length and width add to half of the perimeter and share 18 in the ratio 2:1. 

The length is 12 cm and the width is 6 cm, giving an area of 72 cm 2 .

8) It’s all prime

The sum of three prime numbers is equal to another prime number.

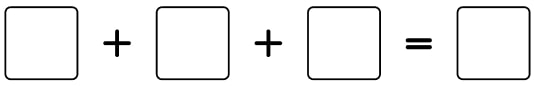
If the sum is less than 30, how many different solutions are possible?

There are 6 solutions. 

2 can never be used as it would force two more odd primes into the sum to make the total even.

9) Unequal share

Bob and Jane have £10 altogether. Jane has £1.60 more than Bob. Bob spends one third of his money. How much money have Bob and Jane now got in total?

Initially Bob has £4.20 and Jane has £5.80. Bob spends £1.40, meaning the total £10 has been reduced by £1.40, leaving £8.60 after the subtraction.

10) Somewhere between

Fred says, “An easy way to find any fraction which is between two other fractions is to just add the numerators and add the denominators.” Is Fred correct?

Solution 

Fred is correct. His method does work and can be shown algebraically which could be a good problem for higher tier learners to try.

If we use these two fractions \frac{3}{8} and \frac{5}{12} , Fred’s method gives us \frac{8}{20} = \frac{2}{5}

\frac{3}{8} = \frac{45}{120} , \frac{2}{5} = \frac{48}{120} , \frac{5}{12} = \frac{50}{120} . So \frac{3}{8} < \frac{2}{5} < \frac{5}{12}

The next 10 questions are crossover questions which could appear on both Foundation and Higher tier exam papers. We have provided solutions for each and, for the first three questions, problem solving strategies to support learners.

11) What’s the difference?

An arithmetic sequence has an nth term in the form an+b .

4 is in the sequence.

16 is in the sequence.

8 is not in the sequence.

-2 is the first term of the sequence.

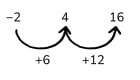
What are the possible values of a and b ?

• We know that the first number in the sequence is -2 and 4 is in the sequence. Can we try making a sequence to fit? Would using a number line help?
• Try looking at the difference between the numbers we know are in the sequence.

If we try forming a sequence from the information, we get this:

We can now try to fill in the missing numbers, making sure 8 is not in the sequence. Going up by 2 would give us 8, so that won’t work.

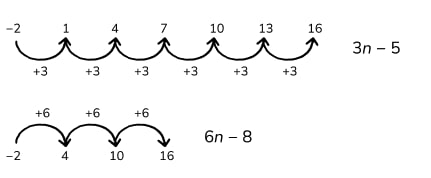
The only solutions are 6 n -8 and 3 n -5.

12) Equation of the hypotenuse

The diagram shows a straight line passing through the axes at point P and Q .

Q has coordinate (8, 0). M is the midpoint of PQ and MQ has a length of 5 units.

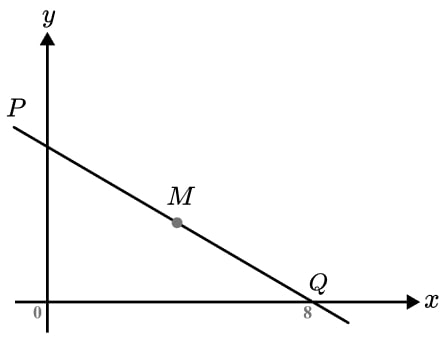
Find the equation of the line PQ .

• We know MQ is 5 units, what is PQ and OQ ?
• What type of triangle is OPQ ?
• Can we find OP if we know PQ and OQ ?
• A line has an equation in the form y=mx+c . How can we find m ? Do we already know c ?

PQ is 10 units. Using Pythagoras’ Theorem OP = 6

The gradient of the line will be \frac{-6}{8} = -\frac{3}{4} and P gives the intercept as 6.

13) What a waste

Harry wants to cut a sector of radius 30 cm from a piece of paper measuring 30 cm by 20 cm. 

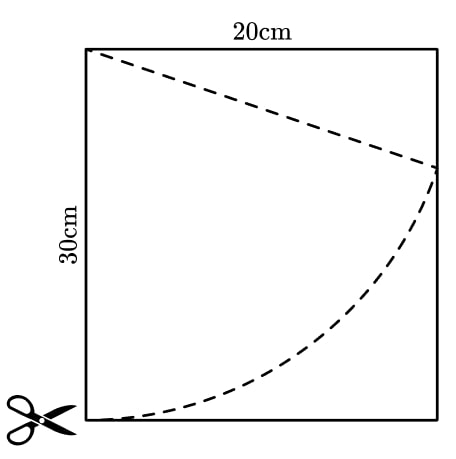
What percentage of the paper will be wasted?

• What information do we need to calculate the area of a sector? Do we have it all?
• Would drawing another line on the diagram help find the angle of the sector?

The angle of the sector can be found using right angle triangle trigonometry.

The angle is 41.81°.

This gives us the area of the sector as 328.37 cm 2 .

The area of the paper is 600 cm 2 .

The area of paper wasted would be 600 – 328.37 = 271.62 cm 2 .

The wasted area is 45.27% of the paper.

14) Tri-polygonometry

The diagram shows part of a regular polygon and a right angled triangle. ABC is a straight line. Find the sum of the interior angles of the polygon.

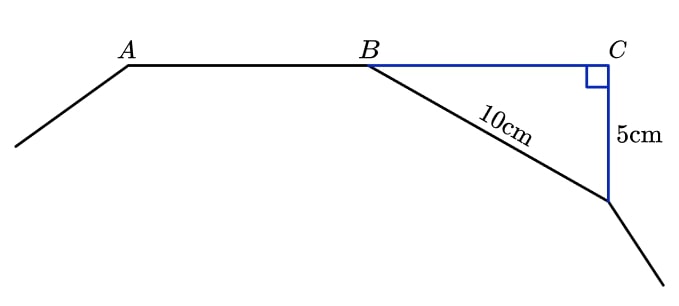
Finding the angle in the triangle at point B gives 30°. This is the exterior angle of the polygon. Dividing 360° by 30° tells us the polygon has 12 sides. Therefore, the sum of the interior angles is 1800°.

15) That’s a lot of Pi

A block of ready made pastry is a cuboid measuring 3 cm by 10 cm by 15 cm. 

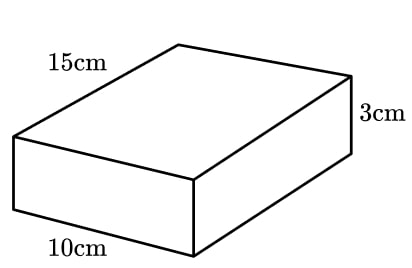
Anne is making 12 pies for a charity event. For each pie, she needs to cut a circle of pastry with a diameter of 18 cm from a sheet of pastry 0.5 cm thick.

How many blocks of pastry will Anne need to buy?

The volume of one block of pastry is 450 cm 3 . 

The volume of one cylinder of pastry is 127.23 cm 3 .

12 pies will require 1526.81 cm 3 .

Dividing the volume needed by 450 gives 3.39(…). 

Rounding this up tells us that 4 pastry blocks will be needed.

16) Is it right?

A triangle has sides of (x+4) cm, (2x+6) cm and (3x-2) cm. Its perimeter is 80 cm.

Show that the triangle is right angled and find its area.

Forming an equation gives 6x+8=80

This gives us x=12 and side lengths of 16 cm, 30 cm and 34 cm.

Using Pythagoras’ Theorem

16 2 +30 2 =1156 

Therefore, the triangle is right angled.

The area of the triangle is (16 x 30) ÷ 2 = 240 cm 2 .

17) Pie chart ratio

The pie chart shows sectors for red, blue and green. 

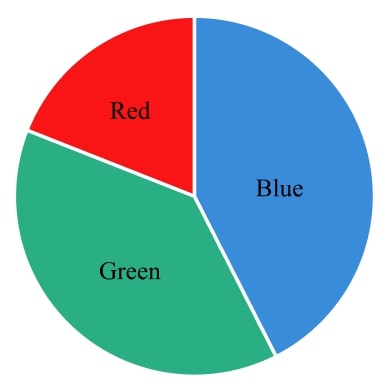
The ratio of the angles of the red sector to the blue sector is 2:7. 

The ratio of the angles of the red sector to the green sector is 1:3. 

Find the angles of each sector of the pie chart.

Multiplying the ratio of red : green by 2, it can be written as 2:6. 

Now the colour each ratio has in common, red, has equal parts in each ratio.

The ratio of red:blue is 2:7, this means red:blue:green = 2:7:6.

Sharing 360° in this ratio gives red:blue:green = 48°:168°:144°.

18) DIY Simultaneously

Mr Jones buys 5 tins of paint and 4 rolls of decorating tape. The total cost was £167.

The next day he returns 1 unused tin of paint and 1 unused roll of tape. The refund amount is exactly the amount needed to buy a fan heater that has been reduced by 10% in a sale. The fan heater normally costs £37.50.

Find the cost of 1 tin of paint.    

The sale price of the fan heater is £33.75. This gives the simultaneous equations

p+t = 33.75 and 5 p +4 t = 167.

We only need the price of a tin of paint so multiplying the first equation by 4 and then subtracting from the second equation gives p =32. Therefore, 1 tin of paint costs £32. 

19) Triathlon pace

Jodie is competing in a Triathlon. 

A triathlon consists of a 5 km swim, a 40 km cycle and a 10 km run. 

Jodie wants to complete the triathlon in 5 hours. 

She knows she can swim at an average speed of 2.5 km/h and cycle at an average speed of 25 km/h. There are also two transition stages, in between events, which normally take 4 minutes each.

What speed must Jodie average on the final run to finish the triathlon in 5 hours?

Dividing the distances by the average speeds for each section gives times of 2 hours for the swim and 1.6 hours for the cycle, 216 minutes in total. Adding 8 minutes for the transition stages gives 224 minutes. To complete the triathlon in 5 hours, that would be 300 minutes. 300 – 224 = 76 minutes. Jodie needs to complete her 10 km run in 76 minutes, or \frac{19}{15} hours. This gives an average speed of 7.89 km/h.

20) Indices

a 2x × a y =a 3

(a 3 ) x ÷ a 4y =a 32

Find x and y .

Forming the simultaneous equations

Solving these gives

This final set of 10 questions would appear on the Higher tier only. Here we have just provided the solutions. Try asking your learners to discuss their strategies for each question.  

21) Angles in a polygon

The diagram shows part of a regular polygon.

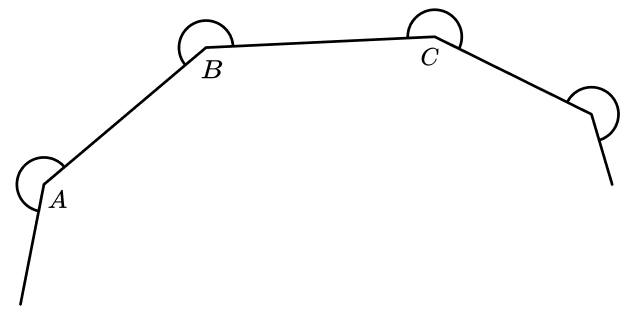
A , B and C are vertices of the polygon. 

The size of the reflex angle ABC is 360° minus the interior angle.

Show that the sum of all of these reflex angles of the polygon will be 720° more than the sum of its interior angles.

Each of the reflex angles is 180 degrees more than the exterior angle: 180 + \frac{360}{n}

The sum of all of these angles is n (180 + \frac{360}{n} ). 

This simplifies to 180 n + 360

The sum of the interior angles is 180( n – 2) = 180 n – 360

The difference is 180 n + 360 – (180 n -360) = 720°

22) Prism and force (Non-calculator)

The diagram shows a prism with an equilateral triangle cross-section.

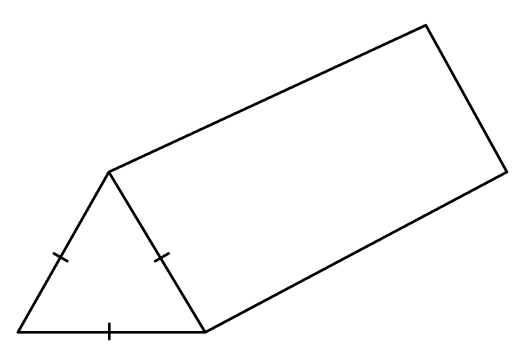
When the prism is placed so that its triangular face touches the surface, the prism applies a force of 12 Newtons resulting in a pressure of \frac{ \sqrt{3} }{4} N/m^{2}

Given that the prism has a volume of 384 m 3 , find the length of the prism.

Pressure = \frac{Force}{Area}

Area = 12÷ \frac{ \sqrt{3} }{4} = 16\sqrt{3} m 2

Therefore, the length of the prism is 384 ÷ 16\sqrt{3} = 8\sqrt{3} m

23) Geometric sequences (Non-calculator)

A geometric sequence has a third term of 6 and a sixth term of 14 \frac{2}{9}

Find the first term of the sequence.

The third term is ar 2 = 6

The sixth term is ar 5 = \frac{128}{9}

Diving these terms gives r 3 = \frac{64}{27}

Giving r = \frac{4}{3}

Dividing the third term twice by \frac{4}{3} gives the first term a = \frac{27}{8}

24) Printing factory

A printing factory is producing exam papers. When all 10 of its printers are working, it can produce all of the exam papers in 12 days.

For the first two days of printing, 3 of the printers are broken.

At the beginning of the third day it is discovered that 2 more printers have broken down, so the factory continues to print with the reduced amount of printers for 3 days. The broken printers are repaired and now all printers are available to print the remaining exams.

How many days in total does it take the factory to produce all of the exam papers?

If we assume one printer prints 1 exam paper per day, 10 printers would print 120 exam papers in 12 days. Listing the number printed each day for the first 5 days gives:

Day 5: 5 

This is a total of 29 exam papers.

91 exam papers are remaining with 10 printers now able to produce a total of 10 exam papers each day. 10 more days would be required to complete the job.

Therefore, 15 days in total are required.

25) Circles

The diagram shows a circle with equation x^{2}+{y}^{2}=13 .

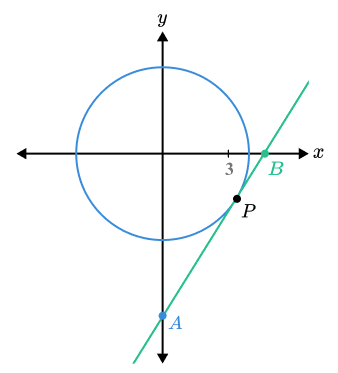
A tangent touches the circle at point P when x=3 and y is negative.

The tangent intercepts the coordinate axes at A and B .

Find the length AB .

Using the equation  x^{2}+y^{2}=13 to find the y value for P gives y=-2 .

The gradient of the radius at this point is - \frac{2}{3} , giving a tangent gradient of \frac{3}{2} .

Using the point (3,-2) in y = \frac {3}{2} x+c gives the equation of the tangent as y = \frac {3}{2} x – \frac{13}{2}

Substituting x=0 and y=0 gives A and B as (0 , -\frac {13}{2}) and ( \frac{13}{3} , 0)

Using Pythagoras’ Theorem gives the length of AB as ( \frac{ 13\sqrt{13} }{6} ) = 7.812.

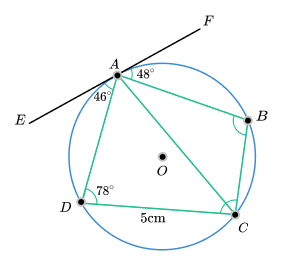
26) Circle theorems

The diagram shows a circle with centre O . Points A, B, C and D are on the circumference of the circle. 

EF is a tangent to the circle at A . 

Angle EAD = 46°

Angle FAB = 48°

Angle ADC = 78°

Find the area of ABCD to the nearest integer.

The Alternate Segment Theorem gives angle ACD as 46° and angle ACB as 48°.

Opposite angles in a cyclic quadrilateral summing to 180° gives angle ABC as 102°.

Using the sine rule to find AC will give a length of 5.899. Using the sine rule again to find BC will give a length of 3.016cm.

We can now use the area of a triangle formula to find the area of both triangles.

0.5 × 5 × 5.899 × sin (46) + 0.5 × 3.016 × 5.899 × sin (48) = 17 units 2 (to the nearest integer).

27) Quadratic function

The quadratic function f(x) = -2x^{2} + 8x +11 has a turning point at P .

Find the coordinate of the turning point after the transformation -f(x-3) .

There are two methods that could be used. We could apply the transformation to the function and then complete the square, or, we could complete the square and then apply the transformation.

Here we will do the latter.

This gives a turning point for f(x) as (2,19).

Applying -f(x-3) gives the new turning point as (5,-19).

28) Probability with fruit

A fruit bowl contains only 5 grapes and n strawberries.

A fruit is taken, eaten and then another is selected.

The probability of taking two strawberries is \frac{7}{22} .

Find the probability of taking one of each fruit. 

There are n+5 fruits altogether.

P(Strawberry then strawberry)= \frac{n}{n+5} × \frac{n-1}{n+4} = \frac{7}{22}

This gives the quadratic equation 15n^{2} - 85n - 140 = 0

This can be divided through by 5 to give 3n^{2} - 17n- 28 = 0

This factorises to (n-7)(3n + 4) = 0

n must be positive so n = 7.

The probability of taking one of each fruit is therefore, \frac{5}{12} × \frac{7}{11} + \frac {7}{12} × \frac {5}{11} = \frac {70}{132}

29) Ice cream tub volume

An ice cream tub in the shape of a prism with a trapezium cross-section has the dimensions shown. These measurements are accurate to the nearest cm.

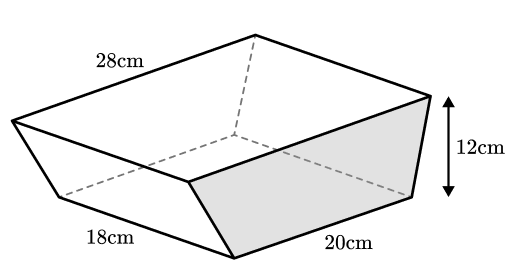
An ice cream scoop has a diameter of 4.5 cm to the nearest millimetre and will be used to scoop out spheres of ice cream from the tub.

Using bounds find a suitable approximation to the number of ice cream scoops that can be removed from a tub that is full.

We need to find the upper and lower bounds of the two volumes. 

Upper bound tub volume = 5665.625 cm 3

Lower bound tub volume = 4729.375 cm 3

Upper bound scoop volume = 49.32 cm 3  

Lower bound scoop volume = 46.14 cm 3  

We can divide the upper bound of the ice cream tub by the lower bound of the scoop to get the maximum possible number of scoops. 

Maximum number of scoops = 122.79

Then divide the lower bound of the ice cream tub by the upper bound of the scoop to get the minimum possible number of scoops.

Minimum number of scoops  = 95.89

These both round to 100 to 1 significant figure, Therefore, 100 scoops is a suitable approximation the the number of scoops.

30) Translating graphs

 The diagram shows the graph of y = a+tan(x-b ).

The graph goes through the points (75, 3) and Q (60, q).

Find exact values of a , b and q .

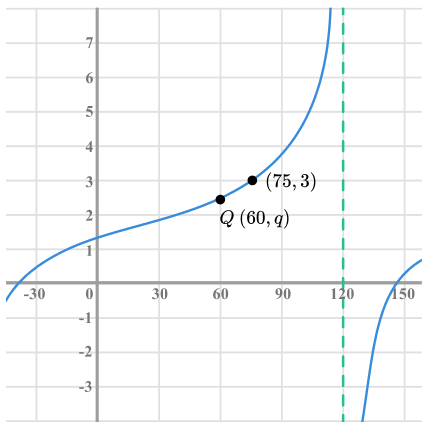
The asymptote has been translated to the right by 30°. 

Therefore, b=30

So the point (45,1) has been translated to the point (75,3). 

Therefore, a=2

We hope these problem solving maths questions will support your GCSE teaching. To get all the solutions and strategies in a printable form, please download the complete resource .

Looking for additional support and resources at KS3? You are welcome to download any of the secondary maths resources from Third Space Learning’s resource library for free. There is a section devoted to GCSE maths revision with plenty of maths worksheets and GCSE maths questions . There are also maths tests for KS3, including a Year 7 maths test , a Year 8 maths test and a Year 9 maths test Other valuable maths practice and ideas particularly around reasoning and problem solving at secondary can be found in our KS3 and KS4 maths blog articles. Try these fun maths problems for KS2 and KS3, SSDD problems , KS3 maths games and 30 problem solving maths questions . For children who need more support, our maths intervention programmes for KS3 achieve outstanding results through a personalised one to one tuition approach.

DO YOU HAVE STUDENTS WHO NEED MORE SUPPORT IN MATHS?

Every week Third Space Learning’s specialist online maths tutors support thousands of students across hundreds of schools with weekly online 1 to 1 maths lessons designed to plug gaps and boost progress.

Since 2013 these personalised one to 1 lessons have helped over 150,000 primary and secondary students become more confident, able mathematicians.

Learn how the programmes are aligned to maths mastery teaching or request a personalised quote for your school to speak to us about your school’s needs and how we can help.

Related articles

Maths Problem Solving: Engaging Your Students And Strengthening Their Mathematical Skills

Free Year 7 Maths Test With Answers And Mark Scheme: Mixed Topic Questions

What Is A Number Square? Explained For Primary School Teachers, Parents & Pupils

What Is Numicon? Explained For Primary School Teachers, Parents And Pupils

FREE Guide to Maths Mastery

All you need to know to successfully implement a mastery approach to mathematics in your primary school, at whatever stage of your journey.

Ideal for running staff meetings on mastery or sense checking your own approach to mastery.

Privacy Overview

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

• Problem Generator
• Mobile Apps
• All Products
• Preferences
• My Apps (API)

Math and Logic Puzzles

If you REALLY like exercising your brain, figuring things 'round and 'round till you explode, then this is the page for you !

Whosoever shall solve these puzzles shall Rule The Universe!

... or at least they should ...

30 Fun Maths Questions with Answers

Table of Contents

Introduction

Mathematics can be fun if you treat it the right way. Maths is nothing less than a game, a game that polishes your intelligence and boosts your concentration. Compared to older times, people have a better and friendly approach to mathematics which makes it more appealing. The golden rule is to know that maths is a mindful activity rather than a task.

There is nothing like hard math problems or tricky maths questions, it’s just that you haven’t explored mathematics well enough to comprehend its easiness and relatability. Maths tricky questions and answers can be transformed into fun math problems if you look at it as if it is a brainstorming session. With the right attitude and friends and teachers, doing math can be most entertaining and delightful.

Math is interesting because a few equations and diagrams can communicate volumes of information. Treat math as a language, while moving to rigorous proof and using logical reason for performing a particular step in a proof or derivation.

Treating maths as a language totally eradicates the concept of hard math problems or tricky maths questions from your mind. Introducing children to fun maths questions can create a strong love and appreciation for maths at an early age. This way you are setting up the child’s successful future. Fun math problems will urge your child to choose to solve it over playing bingo or baking.

Apparently, there are innumerable methods to make easy maths tricky questions and answers. This includes the inception of the ideology that maths is simpler than their fear. This can be done by connecting maths with everyday life. Practising maths with the aid of dice, cards, puzzles and tables reassures that your child effectively approaches Maths.

If you wish to add some fun and excitement into educational activities, also check out

• Check out some mind-blowing Math Magic Tricks!
• Mental Maths: How to Improve it?

Cuemath is one of the world's leading math learning platforms that offers LIVE 1-to-1 online math classes for grades K-12 . Our mission is to transform the way children learn math, to help them excel in school and competitive exams. Our expert tutors conduct 2 or more live classes per week, at a pace that matches the child's learning needs.

Fun Maths Questions with answers - PDF

Here is the Downloadable PDF that consists of Fun Math questions. Click the Download button to view them.

Here are some fun, tricky and hard to solve maths problems that will challenge your thinking ability.

Answer: is 3, because ‘six’ has three letters

What is the number of parking space covered by the car?

This tricky math problem went viral a few years back after it appeared on an entrance exam in Hong Kong… for six-year-olds. Supposedly the students had just 20 seconds to solve the problem!

Believe it or not, this “math” question actually requires no math whatsoever. If you flip the image upside down, you’ll see that what you’re dealing with is a simple number sequence.

Replace the question mark in the above problem with the appropriate number.

Which number is equivalent to 3^(4)÷3^(2)

This problem comes straight from a standardized test given in New York in 2014.

There are 49 dogs signed up for a dog show. There are 36 more small dogs than large dogs. How many small dogs have signed up to compete? 

This question comes directly from a second grader's math homework.

To figure out how many small dogs are competing, you have to subtract 36 from 49 and then divide that answer, 13 by 2, to get 6.5 dogs, or the number of big dogs competing. But you’re not done yet! You then have to add 6.5 to 36 to get the number of small dogs competing, which is 42.5. Of course, it’s not actually possible for half a dog to compete in a dog show, but for the sake of this math problem let’s assume that it is.

Add 8.563 and 4.8292.

Adding two decimals together is easier than it looks. Don’t let the fact that 8.563 has fewer numbers than 4.8292 trip you up. All you have to do is add a 0 to the end of 8.563 and then add like you normally would.

I am an odd number. Take away one letter and I become even. What number am I?

Answer:  Seven (take away the ‘s’ and it becomes ‘even’).

Using only an addition, how do you add eight 8’s and get the number 1000?

Answer: 

888 + 88 + 8 + 8 + 8 = 1000

Sally is 54 years old and her mother is 80, how many years ago was Sally’s mother times her age?

41 years ago, when Sally was 13 and her mother was 39.

Which 3 numbers have the same answer whether they’re added or multiplied together?

There is a basket containing 5 apples, how do you divide the apples among 5 children so that each child has 1 apple while 1 apple remains in the basket?

4 children get 1 apple each while the fifth child gets the basket with the remaining apple still in it.

There is a three-digit number. The second digit is four times as big as the third digit, while the first digit is three less than the second digit. What is the number?

Fill in the question mark

Two girls were born to the same mother, at the same time, on the same day, in the same month and the same year and yet somehow they’re not twins. Why not?

Because there was a third girl, which makes them triplets!

A ship anchored in a port has a ladder which hangs over the side. The length of the ladder is 200cm, the distance between each rung in 20cm and the bottom rung touches the water. The tide rises at a rate of 10cm an hour. When will the water reach the fifth rung?

The tide raises both the water and the boat so the water will never reach the fifth rung. 

The day before yesterday I was 25. The next year I will be 28. This is true only one day in a year. What day is my Birthday?  

You have a 3-litre bottle and a 5-litre bottle. How can you measure 4 litres of water by using 3L and 5L bottles? 

Solution 1 :

First, fill 3Lt bottle and pour 3 litres into 5Lt bottle.

Again fill the 3Lt bottle. Now pour 2 litres into the 5Lt bottle until it becomes full.

Now empty 5Lt bottle.

Pour remaining 1 litre in 3Lt bottle into 5Lt bottle.

Now again fill 3Lt bottle and pour 3 litres into 5Lt bottle.

Now you have 4 litres in the 5Lt bottle. That’s it.

Solution 2 :

First, fill the 5Lt bottle and pour 3 litres into 3Lt bottle.

Empty 3Lt bottle.

Pour remaining 2 litres in  5Lt bottle into 3Lt bottle.

Again fill the 5Lt bottle and pour 1 litre into 3 Lt bottle until it becomes full.

3 Friends went to a shop and purchased 3 toys. Each person paid Rs.10 which is the cost of one toy. So, they paid Rs.30 i.e. total amount. The shop owner gave a discount of Rs.5 on the total purchase of 3 toys for Rs.30. Then, among Rs.5, Each person has taken Rs.1 and remaining Rs.2 given to the beggar beside the shop. Now, the effective amount paid by each person is Rs.9 and the amount given to the beggar is Rs.2. So, the total effective amount paid is 9*3 = 27 and the amount given to beggar is Rs.2, thus the total is Rs.29. Where has the other Rs.1 gone from the original Rs.30?

The logic is payments should be equal to receipts. We cannot add the amount paid by persons and the amount given to the beggar and compare it to Rs.30.The total amount paid is ₹27. So, from ₹27, the shop owner received 25 rupees and beggar received ₹ 2. Thus, payments are equal to receipts.

How to get a number 100 by using four sevens (7’s) and a one (1)?

Answer 1:   177 – 77 = 100 ;

Answer 2: (7+7) * (7 + (1/7)) = 100 

Move any four matches to get 3 equilateral triangles only (don’t remove matches)

Find the area of the red triangle.

To solve this fun maths question, you need to understand how the area of a parallelogram works. If you already know how the area of a parallelogram and the area of a triangle are related, then adding 79 and 10 and subsequently subtracting 72 and 8 to get 9 should make sense.

 How many feet are in a mile? 

Solve  - 15+ (-5x) =0

What is 1.92÷3

A man is climbing up a mountain which is inclined. He has to travel 100 km to reach the top of the mountain. Every day He climbs up 2 km forward in the day time. Exhausted, he then takes rest there at night time. At night, while he is asleep, he slips down 1 km backwards because the mountain is inclined. Then how many days does it take him to reach the mountain top? 

 If 72 x 96 = 6927, 58 x 87 = 7885, then 79 x 86 = ?

Answer:  

Look at this series: 36, 34, 30, 28, 24, … What number should come next?

  Look at this series: 22, 21, 23, 22, 24, 23, … What number should come next?

If 13 x 12 = 651 & 41 x 23 = 448, then, 24 x 22 =?

Look at this series: 53, 53, 40, 40, 27, 27, … What number should come next?

The ultimate goals of mathematics instruction are students understanding the material presented, applying the skills, and recalling the concepts in the future. There's little benefit in students recalling a formula or procedure to prepare for an assessment tomorrow only to forget the core concept by next week.

Teachers must focus on making sure that the students understand the material and not just memorize the procedures. After you learn the answers to a fun maths question, you begin to ask yourself how you could have missed something so easy. The truth is, most trick questions are designed to trick your mind, which is why the answers to fun maths questions are logical and easy. 

About Cuemath

Cuemath, a student-friendly mathematics and coding platform, conducts regular Online Classes for academics and skill-development, and their Mental Math App, on both iOS and Android , is a one-stop solution for kids to develop multiple skills. Understand the Cuemath Fee structure and sign up for a free trial.

Free Mathematics Tutorials

Free Algebra Questions and Problems with Answers

Free intermediate and college algebra questions and problems are presented along with answers and explanations. Free worksheets to download are also included.

Intermediate Algebra Questions with Answers

• sample 1 .(student generated solutions). Also included are the solutions with full explanations .
• sample 2 .(True / False type). Also included are the solutions with full explanations .
• sample 3 .(student generated solutions). solutions with full explanations are included.
• sample 4 .(True / False type). solutions with full explanations included.
• sample 5 .(Multiple choice questions type). Also included are the solutions with full explanations .
• sample 6 .(True / False type). solutions with full explanations included.

Intermediate Algebra Problems with Detailed Solutions

• Algebra Problems .
• Intermediate Algebra Problems With Answers - sample 1 : equations, system of equations, percent problems, relations and functions.
• Intermediate Algebra Problems With Answers - sample 2 :Find equation of line, domain and range from graph, midpoint and distance of line segments, slopes of perpendicular and parallel lines.
• Intermediate Algebra Problems With Answers - sample 3 : equations and system of equations, quadratic equations, function given by a table, intersections of lines, problems.
• Intermediate Algebra Problems With Answers - sample 4 . Functions, domain, range, zeros.
• Intermediate Algebra Problems With Answers - sample 5 . Scientific Notation
• Intermediate Algebra Problems With Answers - sample 6 . Equations of Lines
• Intermediate Algebra Problems With Answers - sample 7 . Slopes of Lines
• Intermediate Algebra Problems With Answers - sample 8 . Absolute Value Expressions
• Intermediate Algebra Problems With Answers - sample 9 . Solve Absolute Value Equations
• Intermediate Algebra Problems With Answers - sample 10 . Solve Absolute Value Inequalities
• Intermediate Algebra Problems With Answers - sample 11 . Simplify Algebraic Expressions by Removing Brackets
• Intermediate Algebra Problems With Answers - sample 12 . Simplify Algebraic Expressions with Exponents

Intermediate Algebra Worksheets

• Worksheet (1) .
• Worksheet (2) .
• Worksheet (3) .
• Worksheet (4) .
• Worksheet (5) .
• Worksheet (6) .

College Algebra Questions with Answers

• sample 1 .(multiple choice questions). Also Detailed solutions with full explanations are included
• sample 2 . (multiple choice questions)

College Algebra Problems with Answers

• sample 1: Quadratic Functions .
• sample 2: Composite and Inverse Functions .
• sample 3: Exponential and Logarithmic Functions .
• sample 4: Graphs of Functions .
• sample 5: Find Domain and Range of Functions .
• sample 6: Problems on Polynomials : Graphs, Factoring, Finding, Multiplying, Dividing, Factor theorem, Zeros
• sample 7: Equation of Circle : Finding equations, center, radius of circles
• sample 8: Equation of Ellipse : Finding equations, foci, center, vertices of ellipses
• sample 9: Equation of Parabola : Finding equations, focus, vertex, axis, directrix of parabola.
• sample 10: Equation of Hyperbola : Finding equations, foci, center and vertices of hyperbola.

College Algebra Worksheets

• Worksheet (1): Graphs of Basic Functions .
• Worksheet (2): Exponential Growth and Decay Problems .
• Worksheet (3): Graphing Exponential Functions .
• Worksheet (4): Graphing Logarithmic Functions .
• Worksheet (5): Solve Exponential Equations .
• Worksheet (6): Solve Logarithmic Equations .
• Worksheet (7): Multiple Choice Questions on Polynomials and Solutions
• Worksheet (8): Multiple Choice Questions on Rational Functions and Solutions .
• Worksheet (9): Graphing Inverse Functions .

Popular Pages

• Intermediate Algebra Questions With Answers - sample 1
• Algebra Problems
• Intermediate Algebra Questions With Solutions and Explanations - sample 1
• Intermediate Algebra Problems With Answers - sample 1
• Solutions to Algebra Problems

Stay In Touch

• Privacy Policy

• Home   |  
• About   |  
• Contact Us   |  
• Privacy   |  
• Newsletter   |  
• Shop   |  
• 🔍 Search Site
• Easter Color By Number Sheets
• Printable Easter Dot to Dot
• Easter Worksheets for kids
• Kindergarten
• All Generated Sheets
• Place Value Generated Sheets
• Addition Generated Sheets
• Subtraction Generated Sheets
• Multiplication Generated Sheets
• Division Generated Sheets
• Money Generated Sheets
• Negative Numbers Generated Sheets
• Fraction Generated Sheets
• Place Value Zones
• Number Bonds
• Addition & Subtraction
• Times Tables
• Fraction & Percent Zones
• All Calculators
• Fraction Calculators
• Percent calculators
• Area & Volume Calculators
• Age Calculator
• Height Calculator
• Roman Numeral Calculator
• Coloring Pages
• Fun Math Sheets
• Math Puzzles
• Mental Math Sheets
• Online Times Tables
• Online Addition & Subtraction
• Math Grab Packs
• All Math Quizzes
• 1st Grade Quizzes
• 2nd Grade Quizzes
• 3rd Grade Quizzes
• 4th Grade Quizzes
• 5th Grade Quizzes
• 6th Grade Math Quizzes
• Place Value
• Rounding Numbers
• Comparing Numbers
• Number Lines
• Prime Numbers
• Negative Numbers
• Roman Numerals
• Subtraction
• Add & Subtract
• Multiplication
• Fraction Worksheets
• Learning Fractions
• Fraction Printables
• Percent Worksheets & Help
• All Geometry
• 2d Shapes Worksheets
• 3d Shapes Worksheets
• Shape Properties
• Geometry Cheat Sheets
• Printable Shapes
• Coordinates
• Measurement
• Math Conversion
• Statistics Worksheets
• Bar Graph Worksheets
• Venn Diagrams
• All Word Problems
• Finding all possibilities
• Logic Problems
• Ratio Word Problems
• All UK Maths Sheets
• Year 1 Maths Worksheets
• Year 2 Maths Worksheets
• Year 3 Maths Worksheets
• Year 4 Maths Worksheets
• Year 5 Maths Worksheets
• Year 6 Maths Worksheets
• All AU Maths Sheets
• Kindergarten Maths Australia
• Year 1 Maths Australia
• Year 2 Maths Australia
• Year 3 Maths Australia
• Year 4 Maths Australia
• Year 5 Maths Australia
• Meet the Sallies
• Certificates

Pythagoras Theorem Questions

Welcome to our Pythagoras' Theorem Questions area. Here you will find help, support and questions to help you master Pythagoras' Theorem and apply it.

For full functionality of this site it is necessary to enable JavaScript.

Here are the instructions how to enable JavaScript in your web browser .

Pythagoras' Theorem Questions

Here you will find our support page to help you learn to use and apply Pythagoras' theorem.

Please note: Pythagoras' Theorem is also called the Pythagorean Theorem

There are a range of sheets involving finding missing sides of right triangles, testing right triangles and solving word problems using Pythagoras' theorem.

Using these sheets will help your child to:

• learn Pythagoras' right triangle theorem;
• use and apply the theorem in a range of contexts to solve problems.

Pythagoras' Theorem

Pythagoras' theorem - in more detail.

Pythagoras' theorem states that in a right triangle (or right-angled triangle) the sum of the squares of the two smaller sides of the triangle is equal to the square of the hypotenuse.

In other words, \[ a^2 + b^2 = c^2 \]

where c is the hypotenuse (the longest side) and a and b are the other sides of the right triangle.

What does this mean?

This means that for any right triangle, the orange square (which is the square made using the longest side) has the same area as the other two blue squares added together.

Other formulas that can be deduced from the Pythagorean theorem

As a result of the formula \[ a^2 + b^2 = c^2 \] we can also deduce that:

• \[ b^2 = c^2 - a^2 \]
• \[ a^2 = c^2 - b^2 \]
• \[ c = \sqrt{a^2 + b^2} \]
• \[ b = \sqrt {c^2 - a^2} \]
• \[ a = \sqrt {c^2 - b^2} \]

Pythagarean Theorem Examples

Example 1) find the length of the missing side..

In this example, we need to find the hypotenuse (longest side of a right triangle).

So using pythagoras, the sum of the two smaller squares is equal to the square of the hypotenuse.

This gives us \[ 4^2 + 6^2 = ?^2 \]

So \[ ?^2 = 16 + 36 = 52 \]

This gives us \[ ? = \sqrt {52} = 7.21 \; cm \; to \; 2 \; decimal \; places \]

Example 2) Find the length of the missing side.

In this example, we need to find the length of the base of the triangle, given the other two sides.

This gives us \[ ?^2 + 5^2 = 8^2 \]

So \[ ?^2 = 8^2 - 5^2 = 64 - 25 = 39 \]

This gives us \[ ? = \sqrt {39} = 6.25 \; cm \; to \; 2 \; decimal \; places \]

Pythagoras' Theorem Question Worksheets

The following questions involve using Pythagoras' theorem to find the missing side of a right triangle.

The first sheet involves finding the hypotenuse only.

A range of different measurement units have been used in the triangles, which are not drawn to scale.

• Pythagoras Questions Sheet 1
• PDF version
• Pythagoras Questions Sheet 2
• Pythagoras Questions Sheet 3
• Pythagoras Questions Sheet 4

Pythagoras' Theorem Questions - Testing Right Triangles

The following questions involve using Pythagoras' theorem to find out whether or not a triangle is a right triangle, (whether the triangle has a right angle).

If Pythagoras' theorem is true for the triangle, and c 2 = a 2 + b 2 then the triangle is a right triangle.

If Pythagoras' theorem is false for the triangle, and c 2 = a 2 + b 2 then the triangle is not a right triangle.

• Pythagoras Triangle Test Sheet 1
• Pythagoras Triangle Test Sheet 2

Pythagoras' Theorem Questions - Word Problems

The following questions involve using Pythagoras' theorem to solve a range of word problems involving 'real-life' type questions.

On the first sheet, only the hypotenuse needs to be found, given the measurements of the other sides.

Illustrations have been provided to support students solving these word problems.

• Pythagoras Theorem Word Problems 1
• Pythagoras Theorem Word Problems 2

Geometry Formulas

• Geometry Formula Sheet

Here you will find a support page packed with a range of geometric formula.

Included in this page are formula for:

• areas and volumes of 2d and 3d shapes
• interior angles of polygons
• angles of 2d shapes
• triangle formulas and theorems

This page will provide a useful reference for anyone needing a geometric formula.

Triangle Formulas

Here you will find a support page to help you understand some of the special features that triangles have, particularly right triangles.

Using this support page will help you to:

• understand the different types and properties of triangles;
• understand how to find the area of a triangle;
• know and use Pythagoras' Theorem.

All the free printable geometry worksheets in this section support the Elementary Math Benchmarks.

• Geometry Formulas Triangles

Here you will find a range of geometry cheat sheets to help you answer a range of geometry questions.

The sheets contain information about angles, types and properties of 2d and 3d shapes, and also common formulas associated with 2d and 3d shapes.

Included in this page are:

• images of common 2d and 3d shapes;
• properties of 2d and 3d shapes;
• formulas involving 2d shapes, such as area and perimeter, pythagoras' theorem, trigonometry laws, etc;
• formulas involving 3d shapes about volume and surface area.

Using the sheets in this section will help you understand and answer a range of geometry questions.

How to Print or Save these sheets 🖶

Need help with printing or saving? Follow these 3 steps to get your worksheets printed perfectly!

• How to Print support

Subscribe to Math Salamanders News

Sign up for our newsletter to get free math support delivered to your inbox each month. Plus, get a seasonal math grab pack included for free!

• Newsletter Signup

Return to Geometry Section

Return from Pythagoras Theorem Questions to Math Salamanders Homepage

Math-Salamanders.com

The Math Salamanders hope you enjoy using these free printable Math worksheets and all our other Math games and resources.

We welcome any comments about our site or worksheets on the Facebook comments box at the bottom of every page.

New! Comments

TOP OF PAGE

© 2010-2024 Math Salamanders Limited. All Rights Reserved.

• Privacy Policy
• Copyright Policy

Solving Equations Practice Questions

Click here for questions, click here for answers.

equation, solve

GCSE Revision Cards

5-a-day Workbooks

Primary Study Cards

Privacy Policy

Terms and Conditions

Corbettmaths © 2012 – 2024

Question Generator

Enjoy using the site, become a member and enjoy access to all the resources on the site ad-free.

• Math Article

Maths Quiz Questions

We are providing here maths quiz questions for children to help them increase their knowledge of the subject. These questions are prepared based on fundamental mathematical concepts. The problems here are provided with four multiple answers and students have to choose the right answer. The questions here could be solved by students of all the classes from 6 to 10, as they are based on basic arithmetic operations and geometrical concepts. Thus, on solving them they can also participate in quiz competitions conducted in schools.

Solving these quizzes will help students to gain more knowledge and boost their problem-solving skills. These questions are very easy to solve and will not take much time. Hence, it is recommended to all the children to solve each one of them and test their abilities.

Maths Quiz Questions with Answers (MCQs)

Let us answer here some of the quizzes which are based on simple arithmetic concepts. These problems are based on fundamental concepts, which students can easily answer without picking up a pen and paper.

Q.1. What is the sum of 130+125+191?

Q.2: If we minus 712 from 1500, how much do we get?

Q.3: 50 times of 8 is equal to:

Q.4: 110 divided by 10 is:

D. None of these

Q.5: 20+(90÷2) is equal to:

Q.6: The product of 82 and 5 is:

Q.7: Find the missing terms in multiple of 3: 3, 6, 9, __, 15

Q.8: Solve 24÷8+2.

Q.9: Solve: 300 – (150×2)

Q.10: The product of 121 x 0 x 200 x 25 is

Q.11: What is the next prime number after 5?

Also, read:

• Class 8 Maths MCQs
• Class 9 Maths MCQs
• Class 10 Maths MCQs

Maths Quizzes and Answers

Here are some quiz questions which children should be able to answer quickly.

Q.12: The circumference of the circle is also sometimes called:

Answer: Perimeter of a circle

Q.13: 90 – 35 is equal to:

Q.14: 72 divided by 8 is equal to:

Q.15: How many sides does a decagon have?

Answer: Ten

Q.16: Is -5 an integer? Yes or No.

Answer: Yes

Q.17: The value of pi is equal to:

Answer: 22/7 or 3.14

Q.18: 9 x 7 is equal to:

Q.19: Is triangle a two-dimensional or three-dimensional shape?

Answer: A two-dimensional shape

Q.20: An equilateral triangle has two of its sides equal. True or false?

Answer: False

All the sides of the equilateral triangle are equal.

Q.21: 10 is a natural number. True or false?

Answer: True

Q.22: -10 is a whole number. True or false?

Q.23: 8 raised to the power 0 is equal to:

Q.24: The largest 4 digit number is:

Answer: 9999

Q.25: The smallest 4-digit number is:

Answer: 1000

Q.26: The square of 8 is equal to:

8 2 = 8 x 8 = 64

Q.27: The square root of 5 is:

Answer: 2.23

Q.28: 3 is a perfect square. True or False?

Answer: False.

Q.29: Cube of 5 is equal to:

Answer: 125

5 3 = 5 x 5 x 5 = 125

Q.30: Cube root of 1331 is:

1331 = 11 x 11 x 11 = 11 3

Q.31: 27 is a perfect cube. True or False?

27 = 3 x 3 x 3= 3 3

Q.32: A square has all its angles equal to:

Answer: 90 degrees

Q.33: The area of rectangle is equal to:

Answer: Length x Breadth

Q.34: If a is the side of cube, then the volume of the cube is:

Answer: a 3

Q.35: A regular polygon has all its sides:

Answer: Equal

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Great thank you

I am a student

Great work keep it up

thanks byjus because tommorow is my mental maths exam and this quiz increase my confidence to solve the mental maths exam [thanks a lot] .

Best of studying

It was a very nice quiz. I enjoyed answering.

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Brain teaser: Can you solve this simple maths puzzle?

I nternet is an amazing place if you are looking for puzzles, riddles and brain teasers. Social media platforms serve as a healthy medium for engaging in such interesting activities.

Here is one such question that has left the internet baffled.

Question: A man steals a $100 dollar bill from a store's register. Then he buys $70 worth of goods at that store using the $100 bill and gets $30 change. How much did the store lose?

Netizens have been scratching their head to find the right answer to this question.

Riddle explained

In this scenario, the man essentially used the stolen $100 bill to purchase $70 worth of goods, receiving $30 in change. However, it's important to recognize that the $100 bill was never rightfully his to begin with—it was stolen from the store's register. Therefore, the store incurs a loss equivalent to the value of the stolen money, which is $100.

READ ALSO: Optical illusion: Spot the dog around the rocks in under 5 seconds

READ ALSO: Brain Teaser: You are among the elite 1 percent if you can identify the box that contains the car

When the man used the stolen $100 bill to pay for the goods, the store effectively received no payment for the items he took. Despite receiving $30 in change, this does not offset the loss incurred by the theft. The $70 worth of goods obtained through the stolen bill is essentially a loss for the store, as it represents merchandise taken without legitimate payment.

Furthermore, the store suffers additional losses beyond the monetary value of the stolen bill. There are costs associated with investigating the theft, potential loss of trust from customers, and potential impacts on the store's reputation. Therefore, while the immediate monetary loss is $100, the overall impact of the theft on the store's operations and reputation could be far greater.

Solving brain teasers boosts your cognitive function

Solving brain teasers offers numerous benefits for cognitive function and mental agility. These puzzles stimulate critical thinking, problem-solving skills, and creativity, enhancing overall cognitive abilities. Regular engagement with brain teasers can improve memory retention, increase concentration, and boost mental acuity. Furthermore, solving puzzles provides a fun way to challenge the brain, reducing stress and promoting a sense of accomplishment. By incorporating brain teasers into daily routines, individuals can maintain cognitive health, sharpen their minds, and enjoy the satisfaction of overcoming mental challenges.

For more news like this visit TOI . Get all the Latest News , City News , India News , Business News , and Sports News . For Entertainment News , TV News , and Lifestyle Tips visit Etimes