how to solve integral calculus problems

Integral Calculus

Integral calculus helps in finding the anti-derivatives of a function. These anti-derivatives are also called the integrals of the function. The process of finding the anti-derivative of a function is called integration. The inverse process of finding derivatives is finding the integrals. The integral of a function represents a family of curves. Finding both derivatives and integrals form the fundamental calculus. In this topic, we will cover the basics of integrals and evaluating integrals.

What is Integral Calculus?

Integrals are the values of the function found by the process of  integration. The process of getting f(x) from f'(x) is called integration. Integrals assign numbers to functions in a way that describe displacement and motion problems, area and volume problems, and so on that arise by combining all the small data. Given the derivative f’ of the function f, we can determine the function f. Here, the function f is called antiderivative or integral of f’. 

Example: Given: f(x) = x 2 .

Derivative of f(x) = f'(x) = 2x = g(x)

if g(x) = 2x, then anti-derivative of g(x) = ∫ g(x) = x 2 

Definition of Integral

F(x) is called an antiderivative or Newton-Leibnitz integral or primitive of a function f(x) on an interval I. F'(x) = f(x), for every value of x in I.

Integral is the representation of the area of a region under a curve. We approximate the actual value of an integral by drawing rectangles. A definite integral of a function can be represented as the area of the region bounded by its graph of the given function between two points in the line. The area of a region is found by breaking it into thin vertical rectangles and applying the lower and the upper limits , the area of the region is summed up. We specify an integral of a function over an interval on which the integral is defined.

Fundamental Theorems of Integral Calculus

We define integrals as the function of the area bounded by the curve y = f(x), a ≤ x ≤ b, the x-axis, and the ordinates x = a and x =b, where b>a. Let x be a given point in [a,b]. Then \(\int\limits_a^b f(x) dx\) represents the area function. This concept of area function leads to the fundamental theorems of integral calculus.

• First Fundamental Theorem of Integral Calculus
• Second Fundamental Theorem of Integral Calculus

First Fundamental Theorem of Integrals

A(x) = \(\int\limits_a^b f(x) dx\) for all x ≥ a, where the function is continuous on [a,b]. Then A'(x) = f(x) for all x ϵ [a,b]

Second Fundamental Theorem of Integrals

If f is continuous function of x defined on the closed interval [a,b] and F be another function such that d/dx F(x) = f(x) for all x in the domain of f, then \(\int\limits_a^b f(x) dx\) = f(b) -f(a). This is known as the definite integral of f over the range [a,b], a being the lower limit and b the upper limit.

Types of Integrals

Integral calculus is used for solving the problems of the following types.

a) the problem of finding a function if its derivative is given.

b) the problem of finding the area bounded by the graph of a function under given conditions. Thus the Integral calculus is divided into two types.

• Definite Integrals (the value of the integrals are definite)
• Indefinite Integrals (the value of the integral is indefinite with an arbitrary constant, C)

Indefinite Integrals

These are the integrals that do not have a pre-existing value of limits; thus making the final value of integral indefinite. ∫g'(x)dx = g(x) + c. Indefinite integrals belong to the family of parallel curves.

Definite Integrals

The definite integrals have a pre-existing value of limits, thus making the final value of an integral, definite. if f(x) is a function of the curve, then \(\int\limits_a^b f(x) dx = f(b) - f(a)\)

Properties of Integral Calculus

Let us study the properties of indefinite integrals to work on them. 

• The derivative of an integral is the integrand itself. ∫ f(x) dx = f(x) +C
• Two indefinite integrals with the same derivative lead to the same family of curves and so they are equivalent. ∫ [ f(x) dx -g(x) dx] =0
• The integral of the sum or difference of a finite number of functions is equal to the sum or difference of the integrals of the individual functions. ∫ [ f(x) dx+g(x) dx] = ∫ f(x) dx + ∫ g(x) dx
• The constant is taken outside the integral sign. ∫ k f(x) dx = k ∫ f(x) dx, where k ∈ R.
• The previous two properties are combined to get the form: ∫ [k\(_1\)f\(_1\)(x) + k\(_2\)f\(_2\)(x) +... k\(_n\)f\(_n\)(x)] dx = k\(_1\)∫ f\(_1\)(x)dx + k\(_2\)∫ f\(_2\)(x)dx+ ... k\(_n\) ∫ f\(_n\)(x)dx

Integrals Formulas

We can remember the formulas of derivatives of some important functions. Here are the corresponding integrals of these functions that are remembered as standard formulas of integrals.

• ∫ x n dx=x n+1 /n+1+C, where n ≠ -1
• ∫ cosxdx = sinx+C
• ∫ sinx dx = -cosx+C
• ∫ sec 2 x dx = tanx+C
• ∫ cosec 2 x dx = -cotx+C
• ∫ secx tanxdx = secx+C
• ∫ cscx cotx dx = -cscx+C
• ∫1/(√(1-x 2 ))= sin -1 x + C
• ∫-1/(√(1-x 2 ))= cos -1 x + C
• ∫1/(1+x 2 )= tan -1 x + C
• ∫-1/(1+x 2 )= cot -1 x + C
• ∫1/(x√(x 2 -1))= sec -1 x + C
• ∫-1/(x√(x 2 -1))= cosec -1 x + C
• ∫ e x dx=e x  + C
• ∫dx/x=ln|x| + C
• ∫ a x dx=a x /ln a + C

Methods to Find Integrals

There are several methods adopted for finding the indefinite integrals. The prominent methods are:

• Finding integrals by integration by substitution method
• Finding integrals by integration by parts
• Finding integrals by integration by partial fractions.

Finding Integrals by Substitution Method

A few integrals are found by the substitution method. If u is a function of x, then u' = du/dx.

∫ f(u)u' dx = ∫ f(u)du, where u = g(x).

Finding Integrals by Integration by Parts

If two functions are of the product form,  integrals are found by the method of integration by parts.

∫f(x)g(x) dx = f(x)∫ g(x) dx - ∫ (f'(x) ∫g(x) dx) dx. 

Finding Integrals by Integration by Partial Fractions

Integration of rational algebraic functions whose numerator and denominator contain positive integral powers of x with constant coefficients is done by resolving them into partial fractions.

To find ∫ f(x)/g(x) dx, decompose this improper rational function to a proper rational function and then integrate.

∫f(x)/g(x) dx = ∫ p(x)/q(x) + ∫ r(x)/s(x), where g(x) = a(x) . s(x)

Applications of Integral Calculus

Using integration, we can find the distance given the velocity. Definite integrals form the powerful tool to find the area under simple curves, the area bounded by a curve and a line, the area between two curves , the volume of the solids. The displacement and motion problems also find their applications of integrals . The area of the region enclosed between two curves y = f(x) and y = g(x) and the lines x =a, x =b is given by

Area = \(\int\limits_a^b (f(x) -g(x))dx\)

Let us find the area bounded by the curve y = x and y = x 2 that intersect at (0,0)and (1,1).

The given curves are that of a line and a parabola. The area bounded by the curves = \(\int\limits_0^1 (y_2 -y_1)dx\)

Area = \(\int\limits_0^1 (x-x^2)dx\)

= x 2 /2- x 3 /3

= 1/6 sq units.

Important Notes

• The primitive value of the function found by the process of integration is called an integral.
• An integral is a mathematical object that can be interpreted as an area or a generalization of area.
• When a polynomial function is integrated the degree of the integral increases by 1.

☛ Also Check:

• Integration of uv formula
• Definite integral formula

Integral Calculus Examples

Example 1. Find the integral of e 3x

∫ d/dx(f(x)) = ∫ d/dx( e 3x )

We know this is of the form of integral, ∫ d/dx( e ax ) = 1/a e ax + C

∫ d/dx( e 3x ) = 1/3 e 3x + C

Answer: The integral of e 3x = 1/3 e 3x + C

Example 2. Find the integral of cos 3x.

∫ d/dx(f(x)) =∫ cos 3x

thus x = t/3

The given integral becomes ∫1/3(cos t) dt

= 1/3(sin t) + C

= 1/3 sin (3x) + C

Answer: The integral of cos 3x = 1/3 sin (3x) + C

Example 3. Evaluate the integral i = \(\int\limits_2^3\) (x+1) dx

By the 2nd theorem of fundamentals of integrals we know that \(\int\limits_a^b F(x) dx = f(b) - f(a)\)

\(\int\limits_2^3\) (x+1) dx = f(3) -f(2)

f(x) = x 2 /2 + x + C

f(3) = 3 2 /2 +3 = 9/2 + 3 = 15/2

f(2)= 2 2 /2 + 2 = 4/2 + 2 = 4

f(3) -f(2) = 15/2 - 4

Answer: The value of the given integral I = 7/2

go to slide go to slide go to slide

Book a Free Trial Class

Practice Questions on Integrals

go to slide go to slide

FAQs on Integral Calculus

What are integrals.

Integrals are the values of the function found by the process of integration. An integral is defined as the area of the region under the curve that is represented as a function y = f(x).

What is The Integrals Symbol Called?

The ntegrals symbol is ∫. This means that it is bound to a limit from the lower to higher and that the integrals represent the area of the curve under the graph of the function.

What Are The Types of Integrals?

The two types of integrals are definite integral and indefinite integral. The definite integrals are bound by the limits. The indefinite integrals are not bound to pre-existing values.

Can an Integral Have Two Answers?

Yes, an indefinite integral can have infinite answers depending upon the value of the constant term; while a definite integral will be a constant value.

What is a Double Integral Used For?

A double integral is used in order to calculate the areas of regions, find the volumes of a given surface, or also the mean value of any given function in a plane region.

How Do you Find The Integrals?

Finding integrals is the inverse operation of finding the derivatives. A few integrals are remembered as formulas. For example, ∫ x n = x n+1 / (n+1) + C. Thus x 6 = x 6+1 / 6+1 = x 7 / 7 + C. A few integrals use the techniques of integration by parts, integration by partial fractions, substitution method, and so on.

How Do You Use Integrals using Trigonometry?

Use the trigonometric identities and simplify the function into integrable function and then apply the formulas and adopt the integration procedures to find the integrals using trigonometry.

What is The Integral of sin x?

The integral of sine x is -cos x + C. ∫ sin x dX = -cos x + C.

What is Integral Calculus Used For?

We use definite integrals to find the area under the curve or between the curves that are defined by the functions, we find their indefinite integrals using the formulas and the techniques and then find their difference of the integrals applying the limits. We use definite integrals for computing the volumes of 3-d solids. Given the velocity, we can find the distance as the distance is the integral of velocity.

Reset password New user? Sign up

Existing user? Log in

Integration Tricks

Already have an account? Log in here.

• Aareyan Manzoor
• Prasun Biswas
• Henry Maltby
• Christopher Williams
• Andrew Ellinor
• Mike Fuller
• Brandon Monsen
• Hua Zhi Vee
• Arjen Vreugdenhil
• Akeel Howell
• A Former Brilliant Member
• Aditya Khurmi
• Solden Stoll
• Enrique Mendez
• David Holcer

Many challenging integration problems can be solved surprisingly quickly by simply knowing the right technique to apply. While finding the right technique can be a matter of ingenuity, there are a dozen or so techniques that permit a more comprehensive approach to solving definite integrals.

Manipulations of definite integrals may rely upon specific limits for the integral, like with odd and even functions , or they may require directly changing the integrand itself, through some type of substitution . However, most integrals require a combination of techniques, and many of the more complicated approaches, like interpretation as a double integral , require multiple steps to reduce the expression.

Consider, for instance, the antiderivative

\[\displaystyle\int e^{- x^2} \, dx.\]

This is known as the Gaussian integral, after its usage in the Gaussian distribution , and it is well known to have no closed form. However, the improper integral

\[I = \int_0^\infty e^{- x^2} \, dx\]

may be evaluated precisely, using an integration trick . In fact, its value is given by the polar integral

\[I^2 = \int_0^\infty \int_0^\infty e^{-x^2} e^{-y^2} \, dy\, dx = \int_0^{\pi/2} \int_0^\infty r e^{-r^2} \, dr\, d\theta.\]

Without such a method for exact evaluation of the integral, the Gaussian (normal) distribution would be significantly more complicated. Such integrals appear throughout physics , statistics , and mathematics .

Odd and Even Functions

Reflections, cyclic points, inverse functions, integration by parts, trigonometric substitutions, weierstrass substitution, taylor series, differentiation under the integral sign, changing to a double integral, harmonic functions.

An odd function \(o(x)\) satisfies \(o(x) = - o(-x)\) for all \(x\). Therefore, for any finite \(t\),

\[\int_{-t}^t o(x) \, dx = 0.\]

An even function \(e(x)\) satisfies \(e(x) = e(-x)\) for all \(x\). Therefore, for any \(t\),

\[\int_{-t}^t e(x) \, dx = 2 \int_0^t e(x) \, dx.\]

Evaluate \[\int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx.\] Notice that the integrand is an odd function. So, \[\begin{align*} \int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx &= \int_{-1}^{1} \frac{(-x)^3-2(-x)}{\sqrt{(-x)^4+1}} \, d(-x) \\ &= - \int_{-1}^1 \frac{x^3-2x}{\sqrt{x^4+1}} \, dx \\ &= 0. \end{align*}\] The final equivalence comes from the fact that the integral is equal to the negative of itself. Therefore, it is \(0\). \(_\square\)

\[ \large \int _{ -1 }^{ 1 }{ \frac { \sin { x } }{ 1+{ x }^{ 2 }+{ x }^{ 4 } } \, dx } = \, ? \]

A similar method to the above is to reverse the interval of integration: to "integrate backwards." For a function \(f\) and real numbers \(a < b\),

\[\int_a^b f(x) \, dx = \int_a^b f(a+b-x) \, dx.\]

Instead of the function being centered at \(0\), the function is now centered at \(\tfrac{a+b}{2}\). Then,

\[\int_a^b f(x) \, dx = \frac{1}{2} \int_a^b f(x) + f(a+b-x) \, dx.\]

Evaluate \[ \int_3^7 \frac{\ln(x+2)}{\ln\big(24+10x-x^2\big)} \, dx.\] We have \[\begin{align*} \int_3^7 \frac{\ln(x+2)}{\ln\big(24+10x-x^2\big)} \, dx &= \int_3^7 \frac{\ln(x+2)}{\ln(x+2) + \ln(12-x)} \, dx \\\\ &= \frac{1}{2} \int_3^7 \frac{\ln(12-x) + \ln(x+2)}{\ln(x+2) + \ln(12-x)} \, dx \\\\ &= 2.\ _\square \end{align*}\]

Let \(f(x)\) be a real-valued function continuous on \(\left[0,2\right]\) such that \(f(x)=f(2x)\) for all \(x\). If

\[\int_0^1 f(x) dx = 100,\]

then what is the value of

\[\int_0^2 f(x)dx ?\]

Suppose the function \(f\) has bounded antiderivative on \([0, \, \infty]\). Then, via the u-substitution \(x \mapsto \tfrac{1}{x}\),

\[\int_0^\infty f(x) \, dx = \frac{1}{2} \int_0^\infty f(x) + \frac{f\big(\frac{1}{x}\big)}{x^2} \, dx.\]

Evaluate \[ \int_0^\infty \frac{\ln (2x)}{1 + x^2} \, dx.\] We have \[\begin{align} \int_0^\infty \frac{\ln (2x)}{1 + x^2} \, dx &= \frac{1}{2} \int_0^\infty \frac{\ln(2x) + \ln\big(2x^{-1}\big)}{1 + x^2} \, dx \\\\ &= \frac{2\ln 2}{2} \int_0^\infty \frac{1}{1 + x^2} \, dx \\\\ &= \frac{\pi \ln 2}{2}.\ _\square \end{align}\]

Evaluate the integral \(\displaystyle \int_{0}^{\infty} \frac{\ln x}{x^2+2x+4} \, dx.\)

Round your answer to three decimal places.

This section is currently incomplete. Let's join hands to build this wiki. Feel free to add anything you know about this topic!

There are more transformations than simply reflections and inversions that maintain the interval of integration, but they are not as common.

Suppose the function \(f\) is one-to-one and increasing. Then, a geometric equivalence may be established:

\[\int_a^b f(x) \, dx + \int_{f(a)}^{f(b)} f^{-1}(x) \, dx = bf(b) - af(a).\]

Suppose the function \(f\) is one-to-one and decreasing. Then, another geometric equivalence may be established:

\[\int_a^b f(x) \, dx - \int_{f(b)}^{f(a)} f^{-1}(x) \, dx = (b-a)f(b) - a\big(f(a)-f(b)\big).\]

Let \(f(x)\) be a one-to-one continuous function such that \(f(1)=4\) and \(f(6)=2\), and assume \(\displaystyle \int_1^6 f(x) \, dx = 15\). Calculate \(\displaystyle \int_2^4 f^{-1}(x) \, dx\). The region bounded by \(f\), \(x = 1\), and \(y = 2\) must have area \(5\), implying the integral in question corresponds to the area \(5 + 1 \cdot (4 - 2) = \boxed{7}\). The above formula for decreasing functions provides the same answer. \(_\square\)

Integration by parts provides a way to change the integrand directly, and like the exploration of inverse functions, it is a geometric statement. However, this is a statement about the geometry of calculus operators, and any visualization of it would lie in an entirely different space. However, the same intuition can apply. Integration by parts is a very powerful tool, and many problems on this page could be solved by this (and more elementary methods) without the need for anything more complicated.

Integration by parts states that for any differentiable functions \(u(x)\) and \(v(x)\), the following equivalence holds:

\[ \int u(x) v'(x) \, dx = u(x) v(x) - \int v(x) u'(x) \, dx. \]

This can be thought of as a "backwards" application of the product rule .

Evaluate \[\int_1^7 \ln(1 + x) \, dx.\] Let \(u(x) = \ln(1 + x)\) and \(v(x) = x + 1\). Then, \[\begin{align} \int_1^7 \ln(1 + x) \, dx &= \big[(x+1)\ln(x+1)\big]_1^7 - \int_1^7 \frac{x+1}{x+1} \, dx \\ &= 8\ln 8 - 2\ln 2 - 6 \\ &= 22 \ln 2 - 6.\ _\square \end{align}\]

The (adjusted) beta function \(B(m, \, n)\) is defined for nonnegative integers \(m\) and \(n\) as \[B(m, \, n) = \int_0^1 x^{m}(1-x)^{n} \, dx.\] Find a closed form for \(B(m, \, n)\). Note that \(B(0, \, n) = \frac{1}{n+1}\). Now, suppose \(n\) is fixed, and note for \(m > 0\), \[\begin{align} B(m, \, n) &= \int_0^1 x^m (1-x)^n \, dx \\ &= 0 - \frac{m}{n+1} \int_0^1 x^{m-1} \cdot \left(-(1-x)^{n+1}\right) \, dx \\ &= \frac{m}{n+1} B(m-1, \, n+1). \end{align}\] Thus, \(B(m, \, n) = \frac{m}{n+1} \cdot \frac{m-1}{n+2} \cdots \frac{1}{n+m} B(0, n+m) = \frac{m! n!}{(m+n+1)!}.\) \(_\square\) Learn more about the beta function (with correctly off-set indices) here .

\[ \int_0^1 \left(1-x^2\right)^9 x^9 \, dx \]

Let \(I\) denote the value of the integral above. What is the sum of digits of \(I^{-1}?\)

When solving integrals with trigonometric functions, trigonometric identities create shortcuts! The Integration Of Trigonometric Functions wiki goes into this in detail, but below are a few examples.

The first identity is \(\sin^2x+\cos^2x=1.\)

We have \[\begin{align} \int(\sin x+\cos x)^2\, dx &=\int\left(\sin^2x+2\sin x\cos x+\cos^2x\right)\, dx\\ &=\int(1+\sin 2x)\, dx\\ &=x-\dfrac{1}{2}\cos 2x+C, \end{align}\] where \(C\) is the constant of integration.

Here is an example of a less obvious application of that identity:

We have \[\begin{align} \int_0^\frac{\pi}{2}\sin^5x\, dx &=\int_0^\frac{\pi}{2}\sin x\left(1-\cos^2x\right)^2\, dx\\ &=-\int_1^0\left(1-u^2\right)^2\, du\\ &=\int_0^1\left(1-u^2\right)^2\, du\\ &=\frac{8}{15}. \end{align}\]

Other examples that can be used are the double-angle formulas , which can be used in the integrals of \(\sin^2\theta\) and \(\cos^2\theta,\) as well as others.

We have \[\begin{align} \int\frac{\cos 2x}{\sin x+\cos x}\, dx &=\int\frac{\cos^2x-\sin^2x}{\sin x+\cos x}\, dx\\ &=\int(\cos x-\sin x)\, dx\\ &=\sin x+\cos x+C, \end{align}\] where \(C\) is the constant of integration.

Finally, the product-to-sum identities help to solve complex integrals.

We have \[\begin{align} \int\sin 2015x \sin 2016x \, dx &=\dfrac{1}{2}\int(\cos x-\cos 4031x)\, dx\\ &=\dfrac{\sin x}{2}-\dfrac{\sin 4031x}{8062}+C, \end{align}\] where \(C\) is the constant of integration.

One of the most powerful substitutions using trigonometric functions is the Weierstrass substitution of \(t=\tan\frac{\theta}{2}.\) This is most easily seen in rational functions involving trigonometric functions. Through trigonometric identities and manipulation \(\sin\theta=\frac{2t}{1+t^2},\) \(\cos\theta=\frac{1-t^2}{1+t^2},\) and \(d\theta=\frac{2\ dt}{1+t^2}.\) This can often transform the integral into the integral of a rational function, as seen in the following example:

Find the value of \(\displaystyle\int_0^\frac{\pi}{2}\frac{dx}{2+\cos x}.\) Use the Weierstrass substitution \(\cos x=\frac{1-t^2}{1+t^2}\) and \(dx=\frac{2dt}{1+t^2}:\) \[\int_0^\frac{\pi}{2}\frac{dx}{2+\cos x}\ =\int_0^1\frac{\frac{2dt}{1+t^2}}{2+\frac{1-t^2}{1+t^2}}=\int_0^1\frac{2}{t^2+3}dt.\] This integral can be finished by a \(u\)-substitution and application of the derivative of arctangent. \(_\square\)

The Weierstrass substitution can also be applied to a rather common integral, \(\displaystyle\int\csc x\ dx.\) A common method of solving this question is a "clever" multiplication by \(\frac{1}{1},\) but the Weierstrass substitution is easier to apply.

We have \[\int\csc \theta\, d\theta=\int\frac{d\theta}{\sin\theta}=\int\frac{\hspace{3mm} \frac{2dt}{1+t^2}\hspace{3mm} }{\frac{2t}{1+t^2}}=\int\frac{dt}{t}=\ln t+C,\] where \(C\) is the constant of integration. All that's needed is to re-substitute \(t=\tan\frac{\theta}{2}\) to obtain the final value of \[\ln\left(\tan\frac{\theta}{2}\right)+C=-\ln(\cot x+\csc x)+C=\ln\frac{\sin\theta}{\cos\theta+1}+C.\]

A final use of the Weierstrass substitution is the "reverse Weierstrass substitution," which involves simplifying the integral of a rational function with trigonometry.

Find the value of \(\displaystyle\int_0^1\dfrac{\arcsin\frac{2x}{1+x^2}}{1+x^2}\, dx\). Recall that in the Weierstrass substitution, \(\frac{2x}{1+x^2}=\sin\theta\) and \(\frac{2dx}{1+x^2}=d\theta.\) Then the above can be transformed to \[\displaystyle\int_0^\frac{\pi}{2}\frac{\sin^{-1}(\sin\theta)}{2}\, d\theta=\displaystyle\int_0^\frac{\pi}{2}\frac{\theta}{2}\, d\theta.\] This is the integral of a polynomial, which evaluates to \(\frac{\pi^2}{16}.\) \(_\square\)

\[\int_0^1\frac{x^4\left(1-x^2\right)^5}{\left(1+x^2\right)^{10}}\, dx=A\]

Given the above, find \(\frac{1}{A}.\)

Main article: Taylor Series

Some functions like \(\tfrac{1}{1-x}\), \(\ln(1 - x)\), \(\arctan x\), and \(e^x\) have nice Taylor expansions that, together with term-by-term integration, can lead to a closed-form answer. The monotone convergence theorem states that in most cases where the integral does exist (as should generally be the case when evaluating an integral), the summation and integral may be interchanged. For more information, see Double Integrals .

Evaluate \[ \int_0^1 \ln x \ln(1 - x) \, dx.\] Note \[ \int_0^1 \ln x \ln(1-x) \, dx = - \int_0^1 \sum_{k = 1}^\infty \frac{x^k \ln x}{k} \, dx.\] Since the monotone convergence theorem applies here, this is equal to \[\begin{align} - \sum_{k = 1}^\infty \int_0^1 \frac{x^k \ln x}{k} \, dx &= \sum_{k = 1}^\infty \frac{1}{k (k+1)^2} \\ &= \sum_{k = 1}^\infty \frac{1}{k(k + 1)} - \sum_{k = 1}^\infty \frac{1}{(k + 1)^2} \\ &= 2 - \frac{\pi^2}{6}.\ _\square \end{align}\]

Main article: Differentiation under the integral sign

Differentiating under the integral sign is a useful method for evaluating certain integrals which might be harder using other methods. This method of integrating was so frequently used by Richard Feynman that it is often referred to as Feynman's integration trick .

\[\dfrac{d}{dx} \displaystyle \int_{g(x)}^{h(x)} f(x,t)dt = f\big(x,h(x)\big)\dfrac{d}{dx}h(x) - f\big(x,g(x)\big)\dfrac{d}{dx}g(x) + \displaystyle \int_{g(x)}^{h(x)}\dfrac{\partial}{\partial x}f(x,t)dt. \]

Compute \[ \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-7x}}{x} \, dx. \] Let \( I(a) = \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-ax}}{x}\, dx.\) Upon differentiating under the integral sign, the equation becomes \[\begin{align} \dfrac{\partial I}{\partial a} &= \displaystyle \int_{0}^{\infty} \dfrac{\partial }{\partial a}\dfrac{e^{-5x} - e^{-ax}}{x}\, dx \\ &= \displaystyle \int_{0}^{\infty} \dfrac{0 -(-xe^{-ax})}{x}\, dx \\ &= \displaystyle \int_{0}^{\infty} e^{-ax}\, dx. \end{align}\] Now, integrating with respect to \(x\) yields the following: \[ \dfrac{\partial I}{\partial a} = \left[\dfrac{e^{-ax}}{a}\right]_{\infty}^{0} \implies \dfrac{\partial I}{\partial a} = \dfrac{1}{a} .\] Integrating both sides with respect to \(a,\) \[ I(a) = \displaystyle \int \dfrac{1}{a}\, da + C \Rightarrow I(a) = \ln a + C, \qquad (1) \] where \(C\) is the constant of integration. Notice that \( I(5) = \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-5x}}{x}\, dx = \int_{0}^{\infty} 0\, dx = 0. \) Substituting these values in \((1)\) gives \[ 0 = \ln 5 + C \implies C = -\ln 5 \implies I(a) = \ln\dfrac{a}{5}.\] To obtain the required integral, substitute \(a = 7\): \[ I(7) = \ln\dfrac{7}{5} \implies \displaystyle \int_{0}^{\infty} \dfrac{e^{-5x} - e^{-7x}}{x}\, dx = \ln\dfrac{7}{5}. \ _\square\]

Compute \[ \displaystyle \int_{0}^{\infty} \dfrac{\sin x}{x}\, dx. \] Let \( I(a) = \displaystyle \int_{0}^{\infty} e^{-ax}\dfrac{\sin x}{x}\, dx. \) Then differentiating under the integral sign gives \[ \dfrac{\partial I(a)}{\partial a} = \displaystyle \int_{0}^{\infty} \dfrac{\partial}{\partial a} e^{-ax}\dfrac{\sin x}{x}\, dx= -\displaystyle \int_{0}^{\infty} e^{-ax}\sin x\, dx. \] Integrating with respect to \(x,\) \[ \dfrac{\partial I(a)}{\partial a} = \left[\dfrac{e^{-ax}\left(a\sin x + \cos x\right)}{a^{2}+1}\right]_{0}^{\infty} = -\dfrac{1}{1+a^{2}}. \] Integrating with respect to \(a,\) \[ I(a) = \displaystyle \int -\dfrac{1}{1+a^{2}}da = -\tan^{-1} a + C, \] where \(C\) is the constant of integration. Now, \[ \displaystyle \lim_{a\rightarrow \infty} = \displaystyle \int_{0}^{\infty} \displaystyle \lim_{a\rightarrow \infty} e^{-ax}\dfrac{\sin x}{x}dx = 0 .\] Using the above information, \[ 0 = -\displaystyle \lim_{a \rightarrow \infty} \tan^{-1} a + C \Rightarrow C = \dfrac{\pi}{2} \Rightarrow I(a) = \dfrac{\pi}{2} - \tan^{-1} a. \] To get our integral, we let \(a = 0\) to obtain \[ I(0) = \dfrac{\pi}{2} - \tan^{-1} 0 = \dfrac{\pi}{2}. \] Therefore, \( \displaystyle \int_{0}^{\infty} \dfrac{\sin x}{x}\, dx = \dfrac{\pi}{2} . \ _\square\)

\[ \int_0^1 x^{50} (\ln x)^{150} \, dx \]

If the value of the integral above is equal to

\[ \dfrac{A!}{B^C}, \]

where \(A,B,\) and \(C\) are positive integers, find the value of \(A+B+C\).

Bonus : Generalize \( \displaystyle \int_0^1 x^{m} (\ln x)^{n} \, dx \).

Find the value of the following integral:

\[ \displaystyle\int_{0}^{\infty} \dfrac{1}{x} \left(\tan^{-1} \pi x - \tan^{-1}x\right)\,dx.\]

Sometimes, the integrand looks like it has already been integrated. This may signal that the integral is better interpreted as a double integral . There are more possibilities for \(u\)-substitutions when two variables can be manipulated (polar, skewed, etc), and simply changing the order of integration may suffice to simplify the integral.

In many ways, this is a dual method to differentiation under the integral sign. The main difference is that the extra variable is interpreted inside of the variable rather than outside of it. In most cases where one works, both could work; in some cases, only one approach works nicely, so it is good to know both.

Suppose \(a\) and \(b\) are real numbers, \(f\) a function, and \(I = \int_a^b f(x) \, dx.\) If \(f(x) = g(x, s) - g(x, r)\) for some constants \(r\) and \( s\), then \[I = \int_a^b \int_r^s \frac{\partial}{\partial t} g(x,t) \, dt \, dx.\]

Supposing Fubini's theorem holds, the order of integration may be swapped or otherwise altered.

Evaluate \[\int_0^{\infty} \frac{e^{\pi x} - e^{x}}{x(e^{\pi x}+1)(e^{x}+1)} \, dx.\] We have \[ \begin{align*} \int_0^{\infty} \frac{e^{\pi x} - e^{x}}{x(e^{\pi x}+1)(e^{x}+1)} \, dx &= \int_0^\infty \frac{1}{x (e^x + 1)} - \frac{1}{x (e^{\pi x} + 1)} \, dx \\ &= \int_0^\infty \int_1^\pi \frac{e^{tx}}{(e^{tx} + 1)^2} \, dt \, dx \\ &= \int_1^\pi \int_0^\infty \frac{e^{tx}}{(e^{tx} + 1)^2} \, dx \, dt \\ &= \int_1^\pi \left[ - \frac{1}{t (e^{tx} + 1)} \right]_0^\infty \, dt \\ &= \int_1^\pi \frac{1}{(1 + 1)t} \, dt \\ &= \frac{\ln \pi}{2}.\ _\square \end{align*} \]

In complex analysis, a harmonic function is a real-valued function that is the real or imaginary part of a complex-differentiable function. In multivariable calculus, it is a function \(f(x, \, y)\) such that \(\left(\frac{\partial}{\partial x}\right)^2 f + \left( \frac{\partial}{\partial y}\right)^2f = 0.\) Generally, such facts from fields afar are not applicable to the evaluation of real integrals; however, the harmonic functions have a special property that greatly simplifies integration over circles .

Suppose \(f\) is a bivariate harmonic function, \((a, \, b)\) is a point in the plane, and \(r\) is a positive real number. Then, \[ \int_0^{2\pi} f(a + r\cos\theta, \, b + r\sin\theta) \, d\theta = 2\pi f(a, \, b).\]

Evaluate \[\int_0^{2\pi} e^{\cos x} \cos(\sin x) \, dx.\] Consider the function \(f(x, \, y) = e^x \cos y.\) Note that \[ \left(\frac{\partial}{\partial x}\right)^2 f + \left(\frac{\partial}{\partial y}\right)^2 f = e^x \cos y + e^x (- \cos y) = 0.\] Therefore, \(f\) is a harmonic function, and it follows that \[\int_0^{2\pi} e^{\cos x} \cos(\sin x) \, dx = 2\pi e^0 \cos(0) = 2\pi.\ _\square\]

Problem Loading...

Note Loading...

Set Loading...

Definite Integrals

You might like to read Introduction to Integration first!

Integration

The symbol for "Integral" is a stylish "S" (for "Sum", the idea of summing slices):

And then finish with dx to mean the slices go in the x direction (and approach zero in width).

Definite Integral

A Definite Integral has start and end values: in other words there is an interval [a, b].

a and b (called limits, bounds or boundaries) are put at the bottom and top of the "S", like this:

We find the Definite Integral by calculating the Indefinite Integral at a , and at b , then subtracting:

Example: What is

We are being asked for the Definite Integral , from 1 to 2, of 2x  dx

First we need to find the Indefinite Integral .

Using the Rules of Integration we find that ∫ 2x dx = x 2 + C

Now calculate that at 1, and 2:

• At x=1: ∫ 2x dx = 1 2 + C
• At x=2: ∫ 2x dx = 2 2 + C

And "C" gets cancelled out ... so with Definite Integrals we can ignore C .

Check : with such a simple shape, let's also try calculating the area by geometry:

A = 2+4 2 × 1 = 3

Yes, it does have an area of 3.

Notation : It is usual to show the indefinite integral (without the +C) inside square brackets, with the limits a and b after, like this:

Example (continued)

How to show your answer:

Let's try another example:

The Definite Integral, from 0.5 to 1.0, of cos(x) dx:

(Note: x must be in radians )

The Indefinite Integral is: ∫ cos(x) dx = sin(x) + C

We can ignore C for definite integrals (as we saw above) and we get:

And another example to make an important point:

The Definite Integral, from 0 to 1, of sin(x) dx:

The Indefinite Integral is: ∫ sin(x) dx = −cos(x) + C

Since we are going from 0, can we just calculate the integral at x=1 ??

−cos(1) = −0.540...

What? It is negative ? But it looks positive in the graph.

Well ... we made a mistake !

Because we need to subtract the integral at x=0 . We shouldn't assume it is zero.

So let us do it properly, subtracting one from the other:

That's better!

But we can have negative regions , when the curve is below the axis:

The Definite Integral, from 1 to 3, of cos(x) dx:

Notice that some of it is positive, and some negative. The definite integral will work out the net value.

Let us do the calculations:

So there is more negative than positive with a net result of −0.700....

Try integrating cos(x) with different start and end values to see for yourself how positives and negatives work.

Positive Area

But sometimes we want all area treated as positive (without the part below the axis being subtracted).

In that case we must calculate the areas separately , like in this example:

Example: What is the total area between y = cos(x) and the x-axis, from x = 1 to x = 3?

This is like the example we just did, but now we expect that it is all positive (imagine we had to paint it).

So now we have to do the parts separately:

• One for the area above the x-axis
• One for the area below the x-axis

The curve crosses the x-axis at x = π /2 so we have:

From 1 to π /2:

From π /2 to 3:

That last one comes out negative, but we want it to be positive, so:

Total area = 0.158... + 0.859... = 1.017 ...

This is very different from the answer in the previous example.

Oh yes, the function we are integrating must be Continuous between a and b : no holes, jumps or vertical asymptotes (where the function heads up/down towards infinity).

A vertical asymptote between a and b affects the definite integral.

Area above − area below

The integral adds the area above the axis but subtracts the area below, for a "net value":

Adding Functions

The integral of f+g equals the integral of f plus the integral of g :

Reversing the interval

Reversing the direction of the interval gives the negative of the original direction.

Interval of zero length

When the interval starts and ends at the same place, the result is zero:

Adding intervals

We can also add two adjacent intervals together:

The Definite Integral between a and b is the Indefinite Integral at b minus the Indefinite Integral at a .

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

5.3: The Fundamental Theorem of Calculus

• Last updated
• Save as PDF
• Page ID 2513

• Gilbert Strang & Edwin “Jed” Herman

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Describe the meaning of the Mean Value Theorem for Integrals.
• State the meaning of the Fundamental Theorem of Calculus, Part 1.
• Use the Fundamental Theorem of Calculus, Part 1, to evaluate derivatives of integrals.
• State the meaning of the Fundamental Theorem of Calculus, Part 2.
• Use the Fundamental Theorem of Calculus, Part 2, to evaluate definite integrals.
• Explain the relationship between differentiation and integration.

In the previous two sections, we looked at the definite integral and its relationship to the area under the curve of a function. Unfortunately, so far, the only tools we have available to calculate the value of a definite integral are geometric area formulas and limits of Riemann sums, and both approaches are extremely cumbersome. In this section we look at some more powerful and useful techniques for evaluating definite integrals.

These new techniques rely on the relationship between differentiation and integration. This relationship was discovered and explored by both Sir Isaac Newton and Gottfried Wilhelm Leibniz (among others) during the late 1600s and early 1700s, and it is codified in what we now call the Fundamental Theorem of Calculus , which has two parts that we examine in this section. Its very name indicates how central this theorem is to the entire development of calculus.

Isaac Newton ’s contributions to mathematics and physics changed the way we look at the world. The relationships he discovered, codified as Newton’s laws and the law of universal gravitation, are still taught as foundational material in physics today, and his calculus has spawned entire fields of mathematics.

Before we get to this crucial theorem, however, let’s examine another important theorem, the Mean Value Theorem for Integrals, which is needed to prove the Fundamental Theorem of Calculus.

The Mean Value Theorem for Integrals

The Mean Value Theorem for Integrals states that a continuous function on a closed interval takes on its average value at the same point in that interval. The theorem guarantees that if \(f(x)\) is continuous, a point \(c\) exists in an interval \([a,b]\) such that the value of the function at \(c\) is equal to the average value of \(f(x)\) over \([a,b]\). We state this theorem mathematically with the help of the formula for the average value of a function that we presented at the end of the preceding section.

Theorem \(\PageIndex{1}\): The Mean Value Theorem for Integrals

If \(f(x)\) is continuous over an interval \([a,b]\), then there is at least one point \(c∈[a,b]\) such that

\[f(c)=\dfrac{1}{b−a}∫^b_af(x)\,dx. \nonumber \]

This formula can also be stated as

\[∫^b_af(x)\,dx=f(c)(b−a). \label{meanvaluetheorem} \]

Since \(f(x)\) is continuous on \([a,b]\), by the extreme value theorem (see section on Maxima and Minima), it assumes minimum and maximum values—\(m\) and \(M\), respectively—on \([a,b]\). Then, for all \(x\) in \([a,b]\), we have \(m≤f(x)≤M.\) Therefore, by the comparison theorem (see Section on The Definite Integral), we have

\[ m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]

Dividing by \(b−a\) gives us

\[ m≤\frac{1}{b−a}∫^b_af(x)\,dx≤M. \nonumber \]

Since \(\displaystyle \frac{1}{b−a}∫^b_a f(x)\,dx\) is a number between \(m\) and \(M\), and since \(f(x)\) is continuous and assumes the values \(m\) and \(M\) over \([a,b]\), by the Intermediate Value Theorem, there is a number \(c\) over \([a,b]\) such that

\[ f(c)=\frac{1}{b−a}∫^b_a f(x)\,dx, \nonumber \]

and the proof is complete.

Example \(\PageIndex{1}\): Finding the Average Value of a Function

Find the average value of the function \(f(x)=8−2x\) over the interval \([0,4]\) and find \(c\) such that \(f(c)\) equals the average value of the function over \([0,4].\)

The formula states the mean value of \(f(x)\) is given by

\[\displaystyle \frac{1}{4−0}∫^4_0(8−2x)\,dx. \nonumber \]

We can see in Figure \(\PageIndex{1}\) that the function represents a straight line and forms a right triangle bounded by the \(x\)- and \(y\)-axes. The area of the triangle is \(A=\frac{1}{2}(base)(height).\) We have

\[A=\dfrac{1}{2}(4)(8)=16. \nonumber \]

The average value is found by multiplying the area by \(1/(4−0).\) Thus, the average value of the function is

\[\dfrac{1}{4}(16)=4 \nonumber \]

Set the average value equal to \(f(c)\) and solve for \(c\).

\[ \begin{align*} 8−2c =4 \nonumber \\[4pt] c =2 \end{align*}\]

At \(c=2,f(2)=4\).

Exercise \(\PageIndex{1}\)

Find the average value of the function \(f(x)=\dfrac{x}{2}\) over the interval \([0,6]\) and find c such that \(f(c)\) equals the average value of the function over \([0,6].\)

Use the procedures from Example \(\PageIndex{1}\) to solve the problem

The average value is \(1.5\) and \(c=3\).

Example \(\PageIndex{2}\): Finding the Point Where a Function Takes on Its Average Value

Given \(\displaystyle ∫^3_0x^2\,dx=9\), find \(c\) such that \(f(c)\) equals the average value of \(f(x)=x^2\) over \([0,3]\).

We are looking for the value of \(c\) such that

\[f(c)=\frac{1}{3−0}∫^3_0x^2\,\,dx=\frac{1}{3}(9)=3. \nonumber \]

Replacing \(f(c)\) with \(c^2\), we have

\[ \begin{align*} c^2 &=3 \\[4pt] c &= ±\sqrt{3}. \end{align*}\]

Since \(−\sqrt{3}\) is outside the interval, take only the positive value. Thus, \(c=\sqrt{3}\) (Figure \(\PageIndex{2}\)).

Exercise \(\PageIndex{2}\)

Given \(\displaystyle ∫^3_0(2x^2−1)\,dx=15\), find \(c\) such that \(f(c)\) equals the average value of \(f(x)=2x^2−1\) over \([0,3]\).

Use the procedures from Example \(\PageIndex{2}\) to solve the problem.

\(c=\sqrt{3}\)

Fundamental Theorem of Calculus Part 1: Integrals and Antiderivatives

As mentioned earlier, the Fundamental Theorem of Calculus is an extremely powerful theorem that establishes the relationship between differentiation and integration, and gives us a way to evaluate definite integrals without using Riemann sums or calculating areas. The theorem is comprised of two parts, the first of which, the Fundamental Theorem of Calculus, Part 1, is stated here. Part 1 establishes the relationship between differentiation and integration.

Theorem \(\PageIndex{2}\): The Fundamental Theorem of Calculus, Part 1

If \(f(x)\) is continuous over an interval \([a,b]\), and the function \(F(x)\) is defined by

\[F(x)=∫^x_af(t)\,dt, \nonumber \]

then \(F′(x)=f(x)\) over \([a,b]\).

Before we delve into the proof, a couple of subtleties are worth mentioning here. First, a comment on the notation. Note that we have defined a function, \(F(x)\), as the definite integral of another function, \(f(t)\), from the point a to the point \(x\). At first glance, this is confusing, because we have said several times that a definite integral is a number, and here it looks like it’s a function. The key here is to notice that for any particular value of \(x\), the definite integral is a number. So the function \(F(x)\) returns a number (the value of the definite integral) for each value of \(x\).

Second, it is worth commenting on some of the key implications of this theorem. There is a reason it is called the Fundamental Theorem of Calculus . Not only does it establish a relationship between integration and differentiation, but also it guarantees that any integrable function has an antiderivative. Specifically, it guarantees that any continuous function has an antiderivative.

Proof: Fundamental Theorem of Calculus, Part 1

Applying the definition of the derivative, we have

\[ \begin{align*} F′(x) &=\lim_{h→0}\frac{F(x+h)−F(x)}{h} \\[4pt] &=\lim_{h→0}\frac{1}{h} \left[∫^{x+h}_af(t)dt−∫^x_af(t)\,dt \right] \\[4pt] &=\lim_{h→0}\frac{1}{h}\left[∫^{x+h}_af(t)\,dt+∫^a_xf(t)\,dt \right] \\[4pt] &=\lim_{h→0}\frac{1}{h}∫^{x+h}_xf(t)\,dt. \end{align*}\]

Looking carefully at this last expression, we see \(\displaystyle \frac{1}{h}∫^{x+h}_x f(t)\,dt\) is just the average value of the function \(f(x)\) over the interval \([x,x+h]\). Therefore, by Equation \ref{meanvaluetheorem}, there is some number \(c\) in \([x,x+h]\) such that

\[ \frac{1}{h}∫^{x+h}_x f(t)\,dt=f(c). \nonumber \]

In addition, since \(c\) is between \(x\) and \(h\), \(c\) approaches \(x\) as \(h\) approaches zero. Also, since \(f(x)\) is continuous, we have

\[ \lim_{h→0}f(c)=\lim_{c→x}f(c)=f(x) \nonumber \]

Putting all these pieces together, we have

\[ F′(x)=\lim_{h→0}\frac{1}{h}∫^{x+h}_x f(t)\,dt=\lim_{h→0}f(c)=f(x), \nonumber \]

Example \(\PageIndex{3}\): Finding a Derivative with the Fundamental Theorem of Calculus

Use the Fundamental Theorem of Calculus, Part 1 to find the derivative of

\[g(x)=∫^x_1\frac{1}{t^3+1}\,dt. \nonumber \]

According to the Fundamental Theorem of Calculus, the derivative is given by

\[g′(x)=\frac{1}{x^3+1}. \nonumber \]

Exercise \(\PageIndex{3}\)

Use the Fundamental Theorem of Calculus, Part 1 to find the derivative of \(\displaystyle g(r)=∫^r_0\sqrt{x^2+4}\,dx\).

Follow the procedures from Example \(\PageIndex{3}\) to solve the problem.

\(g′(r)=\sqrt{r^2+4}\)

Example \(\PageIndex{4}\): Using the Fundamental Theorem and the Chain Rule to Calculate Derivatives

Let \(\displaystyle F(x)=∫^{\sqrt{x}}_1 \sin t \,dt.\) Find \(F′(x)\).

Letting \(u(x)=\sqrt{x}\), we have \(\displaystyle F(x)=∫^{u(x)}_1 \sin t \,dt\).

Thus, by the Fundamental Theorem of Calculus and the chain rule,

\[ F′(x)=\sin(u(x))\frac{du}{\,dx}=\sin(u(x))⋅\left(\dfrac{1}{2}x^{−1/2}\right)=\dfrac{\sin\sqrt{x}}{2\sqrt{x}}. \nonumber \]

Exercise \(\PageIndex{4}\)

Let \(\displaystyle F(x)=∫^{x^3}_1 \cos t\,dt\). Find \(F′(x)\).

Use the chain rule to solve the problem.

\(F′(x)=3x^2\cos x^3\)

Example \(\PageIndex{5}\): Using the Fundamental Theorem of Calculus with Two Variable Limits of Integration

Let \(\displaystyle F(x)=∫^{2x}_x t^3\,dt\). Find \(F′(x)\).

We have \(\displaystyle F(x)=∫^{2x}_x t^3\,dt\). Both limits of integration are variable, so we need to split this into two integrals. We get

\[\begin{align*} F(x) &=∫^{2x}_xt^3\,dt =∫^0_xt^3\,dt+∫^{2x}_0t^3\,dt \\[4pt] &=−∫^x_0t^3\,dt+∫^{2x}_0t^3\,dt. \end{align*}\]

Differentiating the first term, we obtain

\[ \frac{d}{\,dx} \left[−∫^x_0t^3\, dt\right]=−x^3 . \nonumber \]

Differentiating the second term, we first let \((x)=2x.\) Then,

\[\begin{align*} \frac{d}{dx} \left[∫^{2x}_0t^3\,dt\right] &=\frac{d}{dx} \left[∫^{u(x)}_0t^3\,dt \right] \\[4pt] &=(u(x))^3\,du\,\,dx \\[4pt] &=(2x)^3⋅2=16x^3.\end{align*}\]

\[\begin{align*} F′(x) &=\frac{d}{dx} \left[−∫^x_0t^3\,dt \right]+\frac{d}{dx} \left[∫^{2x}_0t^3\,dt\right] \\[4pt] &=−x^3+16x^3=15x^3 \end{align*}\]

Exercise \(\PageIndex{5}\)

Let \(\displaystyle F(x)=∫^{x^2}_x \cos t \, dt.\) Find \(F′(x)\).

Use the procedures from Example \(\PageIndex{5}\) to solve the problem

\(F′(x)=2x\cos x^2−\cos x\)

Fundamental Theorem of Calculus, Part 2: The Evaluation Theorem

The Fundamental Theorem of Calculus, Part 2, is perhaps the most important theorem in calculus. After tireless efforts by mathematicians for approximately 500 years, new techniques emerged that provided scientists with the necessary tools to explain many phenomena. Using calculus, astronomers could finally determine distances in space and map planetary orbits. Everyday financial problems such as calculating marginal costs or predicting total profit could now be handled with simplicity and accuracy. Engineers could calculate the bending strength of materials or the three-dimensional motion of objects. Our view of the world was forever changed with calculus.

After finding approximate areas by adding the areas of n rectangles, the application of this theorem is straightforward by comparison. It almost seems too simple that the area of an entire curved region can be calculated by just evaluating an antiderivative at the first and last endpoints of an interval.

Theorem \(\PageIndex{3}\): The Fundamental Theorem of Calculus, Part 2

If \(f(x)\) is continuous over the interval \([a,b]\) and \(F(x)\) is any antiderivative of \(f(x),\) then

\[ ∫^b_af(x)\,dx=F(b)−F(a). \label{FTC2} \]

We often see the notation \(\displaystyle F(x)|^b_a\) to denote the expression \(F(b)−F(a)\). We use this vertical bar and associated limits \(a\) and \(b\) to indicate that we should evaluate the function \(F(x)\) at the upper limit (in this case, \(b\)), and subtract the value of the function \(F(x)\) evaluated at the lower limit (in this case, \(a\)).

The Fundamental Theorem of Calculus, Part 2 (also known as the evaluation theorem ) states that if we can find an antiderivative for the integrand, then we can evaluate the definite integral by evaluating the antiderivative at the endpoints of the interval and subtracting.

Let \(P={x_i},i=0,1,…,n\) be a regular partition of \([a,b].\) Then, we can write

\[ \begin{align*} F(b)−F(a) &=F(x_n)−F(x_0) \\[4pt] &=[F(x_n)−F(x_{n−1})]+[F(x_{n−1})−F(x_{n−2})] + … + [F(x_1)−F(x_0)] \\[4pt] &=\sum^n_{i=1}[F(x_i)−F(x_{i−1})]. \end{align*} \nonumber \]

Now, we know \(F\) is an antiderivative of \(f\) over \([a,b],\) so by the Mean Value Theorem for derivatives (see The Mean Value Theorem ) for \(i=0,1,…,n\) we can find \(c_i\) in \([x_{i−1},x_i]\) such that

\[F(x_i)−F(x_{i−1})=F′(c_i)(x_i−x_{i−1})=f(c_i)\,Δx. \nonumber \]

Then, substituting into the previous equation, we have

\[ F(b)−F(a)=\sum_{i=1}^nf(c_i)\,Δx. \nonumber \]

Taking the limit of both sides as \(n→∞,\) we obtain

\[ F(b)−F(a)=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=∫^b_af(x)\,dx. \nonumber \]

Example \(\PageIndex{6}\): Evaluating an Integral with the Fundamental Theorem of Calculus

Use Equation \ref{FTC2} to evaluate

\[ ∫^2_{−2}(t^2−4)\,dt. \nonumber \]

Recall the power rule for Antiderivatives:

If \(y=x^n\),

\[∫x^n\,dx=\frac{x^{n+1}}{n+1}+C. \nonumber \]

Use this rule to find the antiderivative of the function and then apply the theorem. We have

\[ \begin{align*} ∫^2_{−2}(t^2−4)dt &=\left( \frac{t^3}{3}−4t \right)∣^2_{−2} \\[4pt] &=\left[\frac{(2)^3}{3}−4(2)\right]−\left[\frac{(−2)^3}{3}−4(−2)\right] \\[4pt] &=\left[\frac{8}{3}−8\right] − \left[−\frac{8}{3}+8 \right] \\[4pt] &=\frac{8}{3}−8+\frac{8}{3}−8 \\[4pt] &=\frac{16}{3}−16=−\frac{32}{3}.\end{align*} \nonumber \]

Notice that we did not include the “\(+ C\)” term when we wrote the antiderivative. The reason is that, according to the Fundamental Theorem of Calculus, Part 2 (Equation \ref{FTC2}), any antiderivative works. So, for convenience, we chose the antiderivative with \(C=0\). If we had chosen another antiderivative, the constant term would have canceled out. This always happens when evaluating a definite integral.

The region of the area we just calculated is depicted in Figure \(\PageIndex{3}\). Note that the region between the curve and the \(x\)-axis is all below the \(x\)-axis. Area is always positive, but a definite integral can still produce a negative number (a net signed area). For example, if this were a profit function, a negative number indicates the company is operating at a loss over the given interval.

Example \(\PageIndex{7}\): Evaluating a Definite Integral Using the Fundamental Theorem of Calculus, Part 2

Evaluate the following integral using the Fundamental Theorem of Calculus, Part 2 (Equation \ref{FTC2}):

\[ ∫^9_1\frac{x−1}{\sqrt{x}}dx. \nonumber \]

First, eliminate the radical by rewriting the integral using rational exponents. Then, separate the numerator terms by writing each one over the denominator:

\[ ∫^9_1\frac{x−1}{x^{1/2}}\,dx=∫^9_1 \left(\frac{x}{x^{1/2}}−\frac{1}{x^{1/2}} \right)\,dx. \nonumber \]

Use the properties of exponents to simplify:

\[ ∫^9_1 \left(\frac{x}{x^{1/2}}−\frac{1}{x^{1/2}}\right)\,dx=∫^9_1(x^{1/2}−x^{−1/2})\,dx. \nonumber \]

Now, integrate using the power rule:

\[ \begin{align*} ∫^9_1(x^{1/2}−x^{−1/2})\,dx &= \left(\frac{x^{3/2}}{\frac{3}{2}}−\frac{x^{1/2}}{\frac{1}{2}}\right)∣^9_1 \\[4pt] &= \left[\frac{(9)^{3/2}}{\frac{3}{2}}−\frac{(9)^{1/2}}{\frac{1}{2}}\right]− \left[\frac{(1)^{3/2}}{\frac{3}{2}}−\frac{(1)^{1/2}}{\frac{1}{2}} \right] \\[4pt] &= \left[\frac{2}{3}(27)−2(3)\right]−\left[\frac{2}{3}(1)−2(1)\right] \\[4pt] &=18−6−\frac{2}{3}+2=\frac{40}{3}. \end{align*} \nonumber \]

See Figure \(\PageIndex{4}\).

Exercise \(\PageIndex{6}\)

Use Note to evaluate \(\displaystyle ∫^2_1x^{−4}\,dx.\)

Use the power rule.

\(\frac{7}{24}\)

Example \(\PageIndex{8}\): A Roller-Skating Race

James and Kathy are racing on roller skates. They race along a long, straight track, and whoever has gone the farthest after 5 sec wins a prize. If James can skate at a velocity of \(f(t)=5+2t\) ft/sec and Kathy can skate at a velocity of \(g(t)=10+\cos\left(\frac{π}{2}t\right)\) ft/sec, who is going to win the race?

We need to integrate both functions over the interval \([0,5]\) and see which value is bigger. For James, we want to calculate

\[ ∫^5_0(5+2t)\,dt. \nonumber \]

Using the power rule, we have

\[ \begin {align*} ∫^5_0(5+2t)\,dt &= \left(5t+t^2\right)∣^5_0 \\[4pt] &=(25+25) \\[4pt] &=50. \end{align*}\]

Thus, James has skated 50 ft after 5 sec. Turning now to Kathy, we want to calculate

\[∫^5_010 + \cos \left(\frac{π}{2}t\right)\, dt. \nonumber \]

We know \(\sin t\) is an antiderivative of \(\cos t\), so it is reasonable to expect that an antiderivative of \(\cos\left(\frac{π}{2}t\right)\) would involve \(\sin\left(\frac{π}{2}t\right)\). However, when we differentiate \(\sin \left(π^2t\right)\), we get \(π^2 \cos\left(π^2t\right)\) as a result of the chain rule, so we have to account for this additional coefficient when we integrate. We obtain

\[ \begin{align*} ∫^5_010+\cos \left(\frac{π}{2}t\right)\,dt &= \left(10t+\frac{2}{π} \sin \left(\frac{π}{2}t\right)\right)∣^5_0 \\[4pt] &=\left(50+\frac{2}{π}\right)−\left(0−\frac{2}{π} \sin 0\right )≈50.6. \end{align*}\]

Kathy has skated approximately 50.6 ft after 5 sec. Kathy wins, but not by much!

Exercise \(\PageIndex{7}\)

Suppose James and Kathy have a rematch, but this time the official stops the contest after only 3 sec. Does this change the outcome?

Change the limits of integration from those in Example \(\PageIndex{7}\).

Kathy still wins, but by a much larger margin: James skates 24 ft in 3 sec, but Kathy skates 29.3634 ft in 3 sec.

A Parachutist in Free Fall

Julie is an avid skydiver with more than 300 jumps under her belt and has mastered the art of making adjustments to her body position in the air to control how fast she falls. If she arches her back and points her belly toward the ground, she reaches a terminal velocity of approximately 120 mph (176 ft/sec). If, instead, she orients her body with her head straight down, she falls faster, reaching a terminal velocity of 150 mph (220 ft/sec).

Since Julie will be moving (falling) in a downward direction, we assume the downward direction is positive to simplify our calculations. Julie executes her jumps from an altitude of 12,500 ft. After she exits the aircraft, she immediately starts falling at a velocity given by \(v(t)=32t.\)

She continues to accelerate according to this velocity function until she reaches terminal velocity. After she reaches terminal velocity, her speed remains constant until she pulls her ripcord and slows down to land.

On her first jump of the day, Julie orients herself in the slower “belly down” position (terminal velocity is 176 ft/sec). Using this information, answer the following questions.

• How long after she exits the aircraft does Julie reach terminal velocity?
• Based on your answer to question 1, set up an expression involving one or more integrals that represents the distance Julie falls after 30 sec.
• If Julie pulls her ripcord at an altitude of 3000 ft, how long does she spend in a free fall?
• Julie pulls her ripcord at 3000 ft. It takes 5 sec for her parachute to open completely and for her to slow down, during which time she falls another 400 ft. After her canopy is fully open, her speed is reduced to 16 ft/sec. Find the total time Julie spends in the air, from the time she leaves the airplane until the time her feet touch the ground. On Julie’s second jump of the day, she decides she wants to fall a little faster and orients herself in the “head down” position. Her terminal velocity in this position is 220 ft/sec. Answer these questions based on this velocity:
• How long does it take Julie to reach terminal velocity in this case?
• Before pulling her ripcord, Julie reorients her body in the “belly down” position so she is not moving quite as fast when her parachute opens. If she begins this maneuver at an altitude of 4000 ft, how long does she spend in a free fall before beginning the reorientation?

Some jumpers wear “ wingsuits ” (Figure \(\PageIndex{6}\)). These suits have fabric panels between the arms and legs and allow the wearer to glide around in a free fall, much like a flying squirrel. (Indeed, the suits are sometimes called “flying squirrel suits.”) When wearing these suits, terminal velocity can be reduced to about 30 mph (44 ft/sec), allowing the wearers a much longer time in the air. Wingsuit flyers still use parachutes to land; although the vertical velocities are within the margin of safety, horizontal velocities can exceed 70 mph, much too fast to land safely.

Answer the following question based on the velocity in a wingsuit.

7. If Julie dons a wingsuit before her third jump of the day, and she pulls her ripcord at an altitude of 3000 ft, how long does she get to spend gliding around in the air

Key Concepts

• The Mean Value Theorem for Integrals states that for a continuous function over a closed interval, there is a value c such that \(f(c)\) equals the average value of the function.
• The Fundamental Theorem of Calculus, Part 1 shows the relationship between the derivative and the integral.
• The Fundamental Theorem of Calculus, Part 2 is a formula for evaluating a definite integral in terms of an antiderivative of its integrand. The total area under a curve can be found using this formula.

Key Equations

• Mean Value Theorem for Integrals

If \(f(x)\) is continuous over an interval \([a,b]\), then there is at least one point \(c∈[a,b]\) such that \[f(c)=\frac{1}{b−a}∫^b_af(x)\,dx.\nonumber \]

• Fundamental Theorem of Calculus, Part 1

If \(f(x)\) is continuous over an interval \([a,b]\), and the function \(F(x)\) is defined by \[ F(x)=∫^x_af(t)\,dt,\nonumber \]

then \[F′(x)=f(x).\nonumber \]

• Fundamental Theorem of Calculus, Part 2

If \(f\) is continuous over the interval \([a,b]\) and \(F(x)\) is any antiderivative of \(f(x)\), then \[∫^b_af(x)\,dx=F(b)−F(a).\nonumber \]

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^{2}-x-6=0
• -x+3\gt 2x+1
• line\:(1,\:2),\:(3,\:1)
• prove\:\tan^2(x)-\sin^2(x)=\tan^2(x)\sin^2(x)
• \frac{d}{dx}(\frac{3x+9}{2-x})
• (\sin^2(\theta))'
• \lim _{x\to 0}(x\ln (x))
• \int e^x\cos (x)dx
• \int_{0}^{\pi}\sin(x)dx
• \sum_{n=0}^{\infty}\frac{3}{2^n}
• Is there a step by step calculator for math?
• Symbolab is the best step by step calculator for a wide range of math problems, from basic arithmetic to advanced calculus and linear algebra. It shows you the solution, graph, detailed steps and explanations for each problem.
• Is there a step by step calculator for physics?
• Symbolab is the best step by step calculator for a wide range of physics problems, including mechanics, electricity and magnetism, and thermodynamics. It shows you the steps and explanations for each problem, so you can learn as you go.
• How to solve math problems step-by-step?
• To solve math problems step-by-step start by reading the problem carefully and understand what you are being asked to find. Next, identify the relevant information, define the variables, and plan a strategy for solving the problem.
• Practice, practice, practice Math can be an intimidating subject. Each new topic we learn has symbols and problems we have never seen. The unknowing...

Please add a message.

Message received. Thanks for the feedback.

• Solve equations and inequalities
• Simplify expressions
• Factor polynomials
• Graph equations and inequalities
• Advanced solvers
• All solvers
• Arithmetics
• Determinant
• Percentages
• Scientific Notation
• Inequalities

The calculus section of QuickMath allows you to differentiate and integrate almost any mathematical expression.

What is calculus?

Calculus is a vast topic, and it forms the basis for much of modern mathematics. The two branches of calculus are differential calculus and integral calculus.

Differential calculus is the study of rates of change of functions. At school, you are introduced to differential calculus by learning how to find the derivative of a function in order to determine the slope of the graph of that function at any point.

Integral calculus is often introduced in school in terms of finding primitive functions (indefinite integrals) and finding the area under a curve (definite integrals).

Differentiate

The differentiate command allows you to find the derivative of an expression with respect to any variable. In the advanced section, you also have the option of specifying arbitrary functional dependencies within your expression and finding higher order derivatives. The differentiate command knows all the rules of differential calculus, including the product rule, the quotient rule and the chain rule.

Go to the Differentiate page

The integrate command can be used to find either indefinite or definite integrals. If an indefinite integral (primitive function) is sought but cannot be found for a particular function, QuickMath will let you know. Definite integrals will always be given in their exact form when possible, but failing this QuickMath will use a numerical method to give you an approximate value.

Go to the Integrate page

The Fundamental Theorem of Calculus

Integrals were evaluated in the previous tutorial by identifying the integral with an appropriate area and then using methods from geometry to find the area. This procedure will succeed only for very simple integrals. The main result of this section, the fundamental theorem of calculus, includes a very important formula for evaluating integrals. This theorem shows us how to evaluate integrals by first evaluating antiderivatives. The theorem establishes an amazing relationship between the integral, which may be interpreted as an area, and the antiderivative, which is inversely related to the derivative; that is, it relates area and the derivative.

Let f be a continuous function on [a, b ], and define a function F by

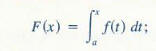
The following theorem is called the fundamental theorem and is a consequence of Theorem 1 . The Fundamental Theorem of Calculus

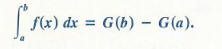
0 = F (a) = G (a) + c

Math Topics

More solvers.

• Add Fractions
• Simplify Fractions

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&