how to solve problems with ratio

One to one maths interventions built for KS4 success

Weekly online one to one GCSE maths revision lessons now available

In order to access this I need to be confident with:

This topic is relevant for:

Ratio Problem Solving

Here we will learn about ratio problem solving, including how to set up and solve problems. We will also look at real life ratio problems.

There are also ratio problem solving worksheets based on Edexcel, AQA and OCR exam questions, along with further guidance on where to go next if you’re still stuck.

What is ratio problem solving?

Ratio problem solving is a collection of word problems that link together aspects of ratio and proportion into more real life questions. This requires you to be able to take key information from a question and use your knowledge of ratios (and other areas of the curriculum) to solve the problem.

A ratio is a relationship between two or more quantities . They are usually written in the form a:b where a and b are two quantities. When problem solving with a ratio, the key facts that you need to know are,

• What is the ratio involved?
• What order are the quantities in the ratio?
• What is the total amount / what is the part of the total amount known?
• What are you trying to calculate ?

As with all problem solving, there is not one unique method to solve a problem. However, this does not mean that there aren’t similarities between different problems that we can use to help us find an answer. 

The key to any problem solving is being able to draw from prior knowledge and use the correct piece of information to allow you to get to the next step and then the solution.

Let’s look at a couple of methods we can use when given certain pieces of information.

When solving ratio problems it is very important that you are able to use ratios. This includes being able to use ratio notation. 

For example, Charlie and David share some sweets in the ratio of 3:5. This means that for every 3 sweets Charlie gets, David receives 5 sweets.

Charlie and David share 40 sweets, how many sweets do they each get?

We use the ratio to divide 40 sweets into 8 equal parts. 

Then we multiply each part of the ratio by 5.

3 x 5:5 x 5 = 15:25

This means that Charlie will get 15 sweets and David will get 25 sweets.

• Dividing ratios

Step-by-step guide: Dividing ratios (coming soon)

Ratios and fractions (proportion problems)

We also need to consider problems involving fractions. These are usually proportion questions where we are stating the proportion of the total amount as a fraction.

Simplifying and equivalent ratios

• Simplifying ratios

Equivalent ratios

Units and conversions ratio questions

Units and conversions are usually equivalent ratio problems (see above).

• If £1:\$1.37 and we wanted to convert £10 into dollars, we would multiply both sides of the ratio by 10 to get £10 is equivalent to \$13.70.
• The scale on a map is 1:25,000. I measure 12cm on the map. How far is this in real life, in kilometres? After multiplying both parts of the ratio by 12 you must then convert 12 \times 25000=300000 \ cm to km by dividing the solution by 100 \ 000 to get 3km.

Notice that for all three of these examples, the units are important. For example if we write the mapping example as the ratio 4cm:1km, this means that 4cm on the map is 1km in real life.

Top tip: if you are converting units, always write the units in your ratio.

Usually with ratio problem solving questions, the problems are quite wordy . They can involve missing values , calculating ratios , graphs , equivalent fractions , negative numbers , decimals and percentages .

Highlight the important pieces of information from the question, know what you are trying to find or calculate , and use the steps above to help you start practising how to solve problems involving ratios.

How to do ratio problem solving

In order to solve problems including ratios:

Identify key information within the question.

Know what you are trying to calculate.

Use prior knowledge to structure a solution.

Explain how to do ratio problem solving

Ratio problem solving worksheet

Get your free ratio problem solving worksheet of 20+ questions and answers. Includes reasoning and applied questions.

Related lessons on ratio

Ratio problem solving is part of our series of lessons to support revision on ratio . You may find it helpful to start with the main ratio lesson for a summary of what to expect, or use the step by step guides below for further detail on individual topics. Other lessons in this series include:

• How to work out ratio  
• Ratio to fraction
• Ratio scale
• Ratio to percentage

Ratio problem solving examples

Example 1: part:part ratio.

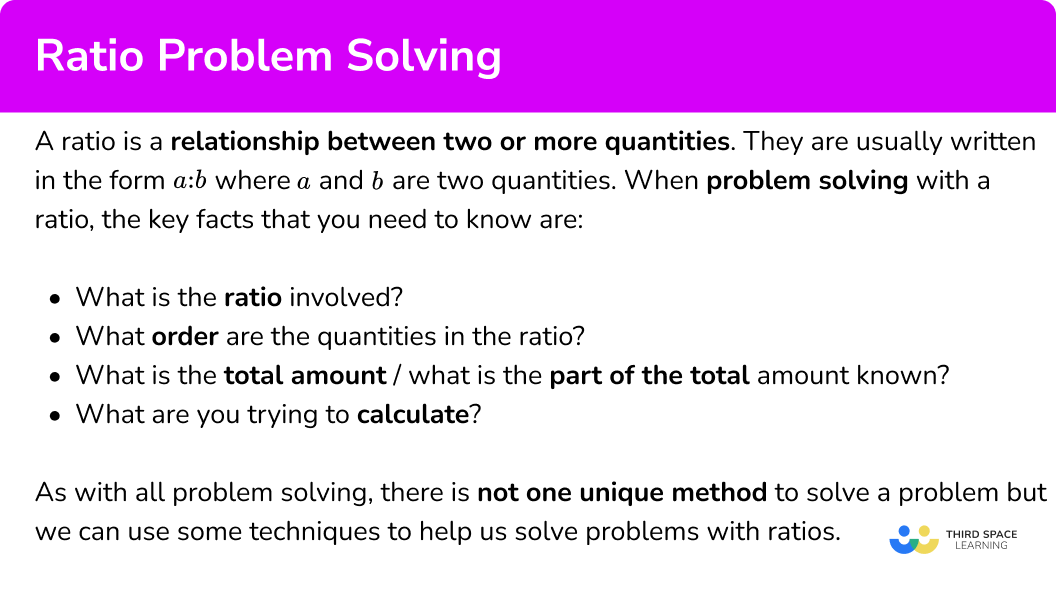
Within a school, the number of students who have school dinners to packed lunches is 5:7. If 465 students have a school dinner, how many students have a packed lunch?

Within a school, the number of students who have school dinners to packed lunches is \bf{5:7.} If \bf{465} students have a school dinner , how many students have a packed lunch ?

Here we can see that the ratio is 5:7 where the first part of the ratio represents school dinners (S) and the second part of the ratio represents packed lunches (P).

We could write this as

Where the letter above each part of the ratio links to the question.

We know that 465 students have school dinner.

2 Know what you are trying to calculate.

From the question, we need to calculate the number of students that have a packed lunch, so we can now write a ratio below the ratio 5:7 that shows that we have 465 students who have school dinners, and p students who have a packed lunch.

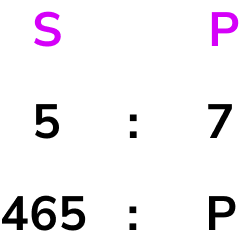
We need to find the value of p.

3 Use prior knowledge to structure a solution.

We are looking for an equivalent ratio to 5:7. So we need to calculate the multiplier. We do this by dividing the known values on the same side of the ratio by each other.

So the value of p is equal to 7 \times 93=651.

There are 651 students that have a packed lunch.

Example 2: unit conversions

The table below shows the currency conversions on one day.

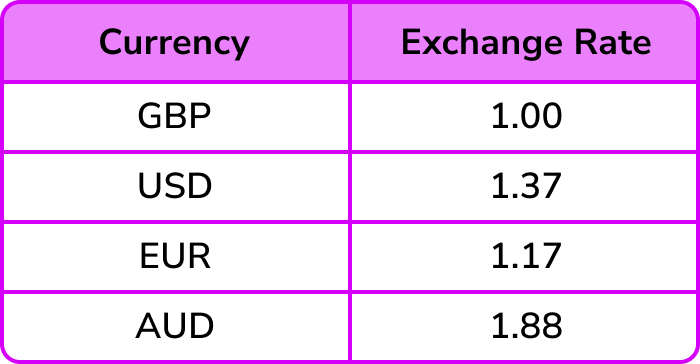
Use the table above to convert £520 (GBP) to Euros € (EUR).

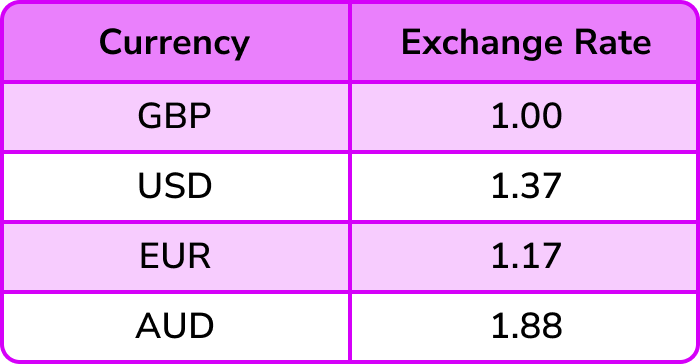
Use the table above to convert \bf{£520} (GBP) to Euros \bf{€} (EUR).

The two values in the table that are important are GBP and EUR. Writing this as a ratio, we can state

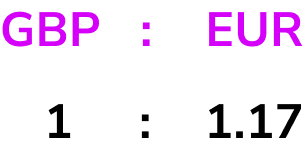
We know that we have £520.

We need to convert GBP to EUR and so we are looking for an equivalent ratio with GBP = £520 and EUR = E.

To get from 1 to 520, we multiply by 520 and so to calculate the number of Euros for £520, we need to multiply 1.17 by 520.

1.17 \times 520=608.4

So £520 = €608.40.

Example 3: writing a ratio 1:n

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the 500ml of concentrated plant food must be diluted into 2l of water. Express the ratio of plant food to water respectively in the ratio 1:n.

Liquid plant food is sold in concentrated bottles. The instructions on the bottle state that the \bf{500ml} of concentrated plant food must be diluted into \bf{2l} of water . Express the ratio of plant food to water respectively as a ratio in the form 1:n.

Using the information in the question, we can now state the ratio of plant food to water as 500ml:2l. As we can convert litres into millilitres, we could convert 2l into millilitres by multiplying it by 1000.

2l = 2000ml

So we can also express the ratio as 500:2000 which will help us in later steps.

We want to simplify the ratio 500:2000 into the form 1:n.

We need to find an equivalent ratio where the first part of the ratio is equal to 1. We can only do this by dividing both parts of the ratio by 500 (as 500 \div 500=1 ).

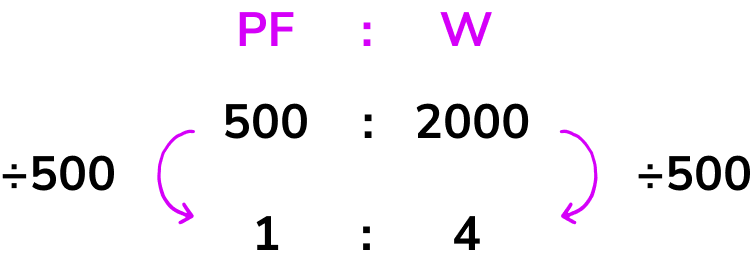
So the ratio of plant food to water in the form 1:n is 1:4.

Example 4: forming and solving an equation

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their age. Kieran is 3 years older than Josh. Luke is twice Josh’s age. If Josh receives £8 pocket money, how much money do the three siblings receive in total?

Three siblings, Josh, Kieran and Luke, receive pocket money per week proportional to their ages. Kieran is \bf{3} years older than Josh . Luke is twice Josh’s age. If Luke receives \bf{£8} pocket money, how much money do the three siblings receive in total ?

We can represent the ages of the three siblings as a ratio. Taking Josh as x years old, Kieran would therefore be x+3 years old, and Luke would be 2x years old. As a ratio, we have

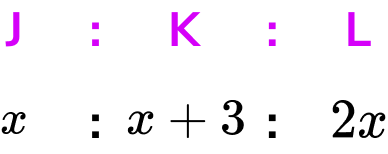
We also know that Luke receives £8.

We want to calculate the total amount of pocket money for the three siblings.

We need to find the value of x first. As Luke receives £8, we can state the equation 2x=8 and so x=4.

Now we know the value of x, we can substitute this value into the other parts of the ratio to obtain how much money the siblings each receive.

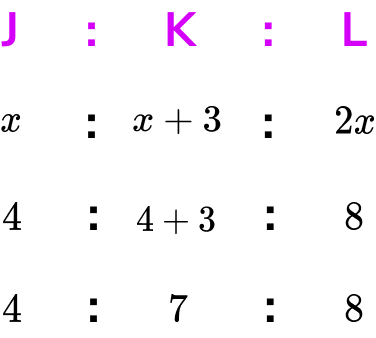
The total amount of pocket money is therefore 4+7+8=£19.

Example 5: simplifying ratios

Below is a bar chart showing the results for the colours of counters in a bag.

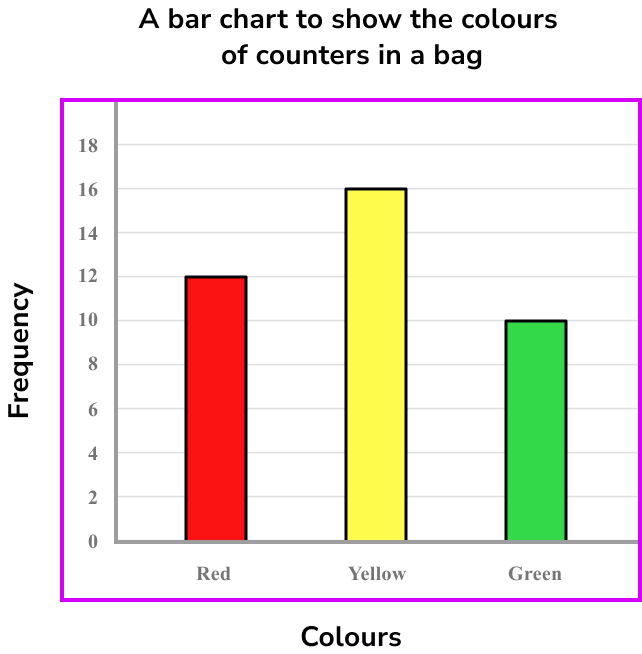
Express this data as a ratio in its simplest form.

From the bar chart, we can read the frequencies to create the ratio.

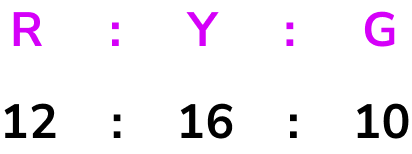
We need to simplify this ratio.

To simplify a ratio, we need to find the highest common factor of all the parts of the ratio. By listing the factors of each number, you can quickly see that the highest common factor is 2.

\begin{aligned} &12 = 1, {\color{red} 2}, 3, 4, 6, 12 \\\\ &16 = 1, {\color{red} 2}, 4, 8, 16 \\\\ &10 = 1, {\color{red} 2}, 5, 10 \end{aligned}

HCF (12,16,10) = 2

Dividing all the parts of the ratio by 2 , we get

Our solution is 6:8:5 .

Example 6: combining two ratios

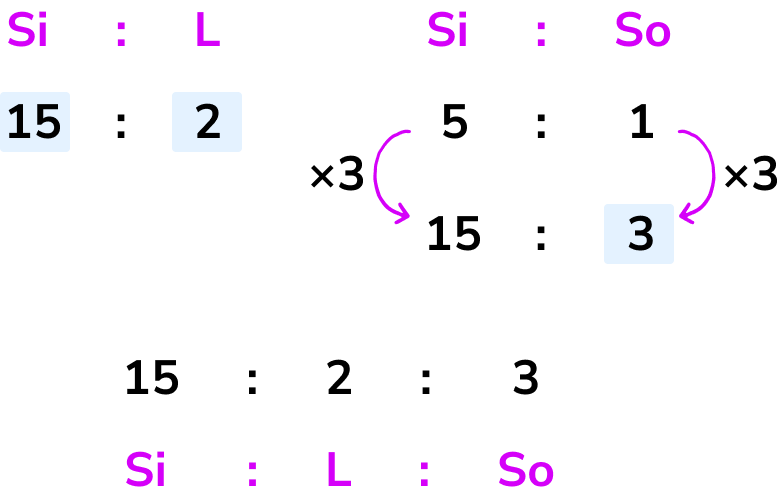
Glass is made from silica, lime and soda. The ratio of silica to lime is 15:2. The ratio of silica to soda is 5:1. State the ratio of silica:lime:soda.

Glass is made from silica, lime and soda. The ratio of silica to lime is \bf{15:2.} The ratio of silica to soda is \bf{5:1.} State the ratio of silica:lime:soda .

We know the two ratios

We are trying to find the ratio of all 3 components: silica, lime and soda.

Using equivalent ratios we can say that the ratio of silica:soda is equivalent to 15:3 by multiplying the ratio by 3.

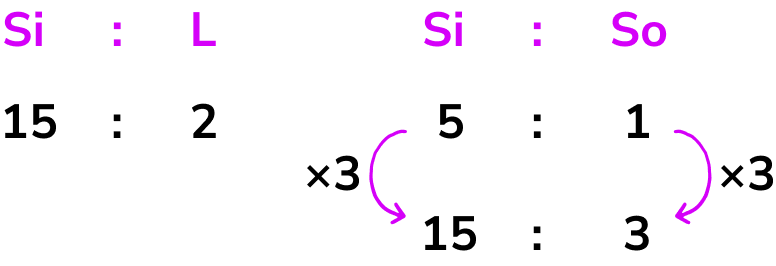
We now have the same amount of silica in both ratios and so we can now combine them to get the ratio 15:2:3.

Example 7: using bar modelling

India and Beau share some popcorn in the ratio of 5:2. If India has 75g more popcorn than Beau, what was the original quantity?

India and Beau share some popcorn in the ratio of \bf{5:2.} If India has \bf{75g} more popcorn than Beau , what was the original quantity?

We know that the initial ratio is 5:2 and that India has three more parts than Beau.

We want to find the original quantity.

Drawing a bar model of this problem, we have

Where India has 5 equal shares, and Beau has 2 equal shares.

Each share is the same value and so if we can find out this value, we can then find the total quantity.

From the question, India’s share is 75g more than Beau’s share so we can write this on the bar model.

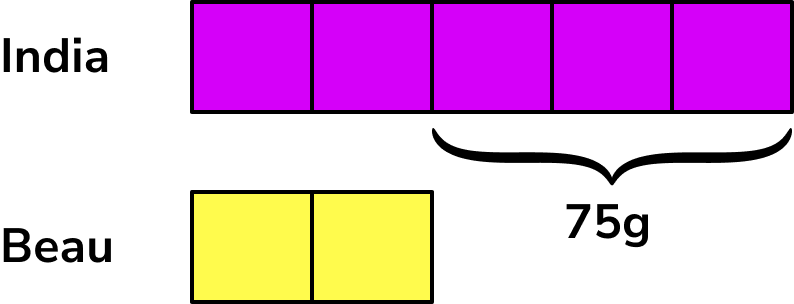
We can find the value of one share by working out 75 \div 3=25g.

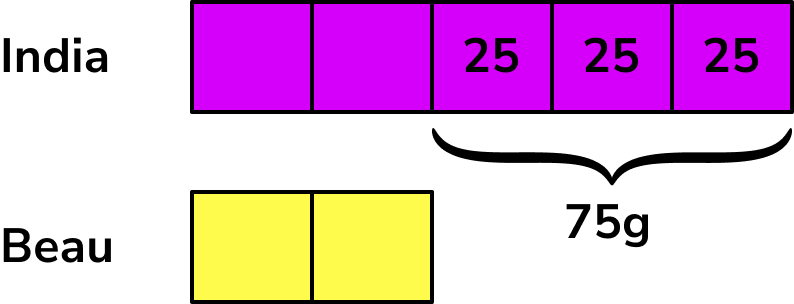
We can fill in each share to be 25g.

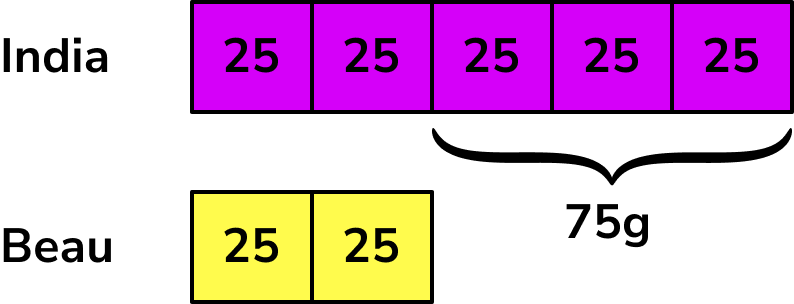
Adding up each share, we get

India = 5 \times 25=125g

Beau = 2 \times 25=50g

The total amount of popcorn was 125+50=175g.

Common misconceptions

• Mixing units

Make sure that all the units in the ratio are the same. For example, in example 6 , all the units in the ratio were in millilitres. We did not mix ml and l in the ratio.

• Ratio written in the wrong order

For example the number of dogs to cats is given as the ratio 12:13 but the solution is written as 13:12.

• Ratios and fractions confusion

Take care when writing ratios as fractions and vice-versa. Most ratios we come across are part:part. The ratio here of red:yellow is 1:2. So the fraction which is red is \frac{1}{3} (not \frac{1}{2} ).

• Counting the number of parts in the ratio, not the total number of shares

For example, the ratio 5:4 has 9 shares, and 2 parts. This is because the ratio contains 2 numbers but the sum of these parts (the number of shares) is 5+4=9. You need to find the value per share, so you need to use the 9 shares in your next line of working.

• Ratios of the form \bf{1:n}

The assumption can be incorrectly made that n must be greater than 1 , but n can be any number, including a decimal.

Practice ratio problem solving questions

1. An online shop sells board games and computer games. The ratio of board games to the total number of games sold in one month is 3:8. What is the ratio of board games to computer games?

8-3=5 computer games sold for every 3 board games.

2. The volume of gas is directly proportional to the temperature (in degrees Kelvin). A balloon contains 2.75l of gas and has a temperature of 18^{\circ}K. What is the volume of gas if the temperature increases to 45^{\circ}K?

3. The ratio of prime numbers to non-prime numbers from 1-200 is 45:155. Express this as a ratio in the form 1:n.

4. The angles in a triangle are written as the ratio x:2x:3x. Calculate the size of each angle.

5. A clothing company has a sale on tops, dresses and shoes. \frac{1}{3} of sales were for tops, \frac{1}{5} of sales were for dresses, and the rest were for shoes. Write a ratio of tops to dresses to shoes sold in its simplest form.

6. During one month, the weather was recorded into 3 categories: sunshine, cloud and rain. The ratio of sunshine to cloud was 2:3 and the ratio of cloud to rain was 9:11. State the ratio that compares sunshine:cloud:rain for the month.

Ratio problem solving GCSE questions

1. One mole of water weighs 18 grams and contains 6.02 \times 10^{23} water molecules.

Write this in the form 1gram:n where n represents the number of water molecules in standard form.

2. A plank of wood is sawn into three pieces in the ratio 3:2:5. The first piece is 36cm shorter than the third piece.

Calculate the length of the plank of wood.

5-3=2 \ parts = 36cm so 1 \ part = 18cm

3. (a) Jenny is x years old. Sally is 4 years older than Jenny. Kim is twice Jenny’s age. Write their ages in a ratio J:S:K.

(b) Sally is 16 years younger than Kim. Calculate the sum of their ages.

Learning checklist

You have now learned how to:

• Relate the language of ratios and the associated calculations to the arithmetic of fractions and to linear functions
• Develop their mathematical knowledge, in part through solving problems and evaluating the outcomes, including multi-step problems
• Make and use connections between different parts of mathematics to solve problems

The next lessons are

• Compound measures
• Best buy maths

Still stuck?

Prepare your KS4 students for maths GCSEs success with Third Space Learning. Weekly online one to one GCSE maths revision lessons delivered by expert maths tutors.

Find out more about our GCSE maths tuition programme.

Privacy Overview

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons
• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.3: Ratios

• Last updated
• Save as PDF
• Page ID 130902

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

You've likely heard the word "ratio" before — it is perhaps one of the most well-known and commonly use mathematical concepts. In this section we'll define what the word ratio actually means, and get practice using ratios to answer questions in various contexts.

In this section, you will learn to:

• Define, recognize, and compute ratios in various forms
• Compare different ratios
• Use ratios to describe and answer contextualized questions
• Compute two specific real-world ratios

Introduction to Ratios

Humans find it useful to compare quantities. Given two quantities, we might want to compare them by using words like larger, smaller, much less than, much more than, and so on. These types of comparisons provide some qualitative information about how two quantities can be related.

Ratios give us a more precise way to compare two quantities. For example, if you're trying to make cookies, your recipe might call for \(2\) cups of flour and \(1\) cup of sugar. In this case, you'll use "one more" cup of flour than sugar. But let's say you wanted to make a big batch -- one that used \(3\) cups of sugar instead of \(1\) cup. In this case, would you still use one more cup of flour -- in this case, \(4\) cups of flour?

If you did this — used \(4\) cups of flour for \(3\) cups of sugar — your cookies would be very sweet and be likely to burn in the oven. The reason is that quantities used in baking are proportional. When you triple the amount of sugar, you also need to triple the amount of flour! That is, you'd need \(2 \times 3 = 6\) cups of flour if you plan to use \(1 \times 3 = 3\) cups of sugar.

The commonality here is not the difference between the two quantities. Rather, it's the fact that in either case, there is twice as much flour as sugar. This is a situation in which a ratio is useful to compare two quantities.

Definition: Ratio

A ratio is a way to describe the relative size of two quantities.

There are several common ways in which ratios are represented. We will study three of them.

It is important to note that these three things are different ways of expressing the same idea. However, some of them, in particular Fraction Notation, can also have slightly different meanings in other contexts.

Each of these notations has their virtues and their drawbacks. The virtue of using Fraction Notation is that it is standard across all of mathematics. The benefit of this is that there are clear rules for how to manipulate fractions, which you can rely upon to help you solve real world problems. One drawback of Fraction Notation is that using fractions tends to make it look like you are considering part of a whole, which may not always be the case when you are using ratios. The virtue of Verbal or Colon Notation is that they both make it clear that you are comparing two quantities. For example, we might say: "at Western Oregon University the ratio of out-of-state to in-state students is about \(1 \colon 4\)." The colon makes it clear that for every out-of-state student there are four in-state students. However, if we wrote instead that the ratio is \(\frac{1}{4}\), it is tempting to jump to the conclusion that we are making some claim about one fourth of the student population. But we are not really talking about one fourth of anything! This is why you will see all of these notations represented both in this textbook and in the broader world.

It is possible for two ratios that look different to actually represent the same ratio! That happens if the numbers in one ratio can be multiplied by the same number to get the other ratio. For example, \(\frac{2}{3}\) and \(\frac{8}{12}\) represent the same ratio, because \(2 \times 4 = 8\) and \(3 \times 4 = 12\). In other words, we can take the ratio \(\frac{2}{3}\), multiply both the top and bottom by 4, and get \(\frac{8}{12}\). Thus, they are equivalent ratios. You may also notice that if you reduce the fraction \(\frac{8}{12}\) by cancelling the common factor of \(4\) from the top and bottom, you get \(\frac{2}{3}\). That's not a coincidence! In general, to compare or easily visualize ratios, it is often helpful to write them in a common way:

Definition: Lowest Terms and Equivalent Ratios

A ratio is in lowest terms if its fractional form has been fully reduced. That is, all common whole number factors on the top and bottom of the fraction have been cancelled out.

Two ratios are  equivalent ratios  if, when reduced to lowest terms, they are identical. 

Let's see an example of how we can write ratios in different ways, and how to put a ratio in lowest terms.

Example \(\PageIndex{1}\)

Write the ratio \(\frac{6}{3}\) using two other types of notation. Then write \(\frac{6}{3}\) in lowest terms. Finally, write three equivalent ratios in fractional form.

First, we will write \(\frac{6}{3}\) in the two other types of notations. They are:

• \(6\) to \(3\)
• \(6 \colon 3\)

Next, we will reduce \(\frac{6}{3}\) to lowest terms. There is a common factor of \(3\) in both the top and bottom of the fraction, so when we cancel those factors out, \(\frac{6}{3}\) reduces to \(\frac{2}{1}\). Now there are no more common factors (besides \(1\), but canceling that does not change the answer). So, this ratio in lowest terms is \(\frac{2}{1}\). Note that this is probably more easily understood than \(\frac{6}{3}\) in most contexts.

Last, we'll find several equivalent ratios. To do that, we'll multiply both the top and bottom of the fraction \(\frac{6}{3}\) by the same numbers. For example, if we multiply both by \(2\), we get \(\frac{12}{6}\). This is equivalent to \(\frac{6}{3}\). We also found that \(\frac{2}{1}\) is equivalent to \(\frac{6}{3}\), since we can multiply both the top and bottom by \(\frac{1}{3}\). Said another way, you can see this by dividing both by the top and bottom numbers by \(3\). 

There are many other equivalent ratios: \(\frac{4}{2}\), \(\frac{10}{5}, \frac{18}{9}, \frac{200}{100}\) — any fraction where the top number is twice the bottom number. This is the essence of equivalent ratios: even though they have different numbers, those two numbers have the same relationship to one another.

Next, we need to understand ratios in context. See if you can answer the question below before revealing the answer!

Example \(\PageIndex{2}\)

The director of an animal shelter is writing a newsletter about the current operations at the shelter. In the animal shelter, there are \(18\) dogs and \(24\) cats. In her newsletter, she wants to list the ratio of cats to dogs in an easy-to-understand way. What sentence should she write?

Here's one possibility: the ratio of cats to dogs in the shelter is \(24 \colon 18\). (Notice that the order matters here!)

That ratio gives an accurate description, but it doesn't lead to an easily visualized comparison for the newsletter readers. So, she should put it in lowest terms. If we rewrite our ratio as \(\frac{24}{18}\), we can reduce this to lowest terms by eliminating a factor of \(6\) from both top and bottom. Then the ratio becomes \(\frac{4}{3}\), which has no more common factors to cancel.

The sentence she writes will be: "There's a \(4\) to \(3\) ratio of cats to dogs in the shelter."

Now, of course, there are many possible good answers to the question above. In this class, grading will be much more fluid than in other math classes, because often there is more than one good answer when we are asked to contextualize mathematics. You should focus on making the mathematics understandable in context. Throughout these notes you will see many more examples of how to do that.

In some contexts, ratios are rounded slightly so they are easier to understand. This happens particularly when the actual quantities being compared are large, but it's helpful to represent the ratio using smaller numbers.

Example \(\PageIndex{3}\)

According to the WOU website , as of 2023, the total enrollment is listed as 3752 students, and the student-to-faculty ratio is listed as \(13 \colon 1\). You want to know how many faculty there are at WOU. How might you find this out, and how do you explain your answer?

To figure this out, we need to find a student-to-faculty ratio that is equivalent to \(13 \colon 1\), but where the number of students is 3752. We will use the a letter, \(x\), to represent the number of faculty. That is, we want to find a value for \(x\) so that

\[3752:x \quad \text{and} \quad 13:1\]

are equivalent ratios. If these are equivalent ratios, then we must be able to multiply 13 by some number to get \(3752\). To find this number, we simply divide \(3752\div 13\), since multiplication and division are inverse operations. This gives us

\[3752 \div 13 = \frac{3752}{13} \approx 288.6\]

using a calculator, rounding to the nearest tenth. That is, \(13 \times 288.6 \approx 3752\). You can check this using a calculator.

In order for these ratios to be equivalent, we have \(1 \times 288.6 = x\). Therefore, it must be \(288.6 = x\), and so there are \(288.6\) faculty at WOU. But this answer is not a whole number, even though it is referring to a number of people. So, what does it mean to have \(288.6\) faculty?

It could mean several things. First, it could mean that some faculty are part-time, which means that they are counted as only part of a whole faculty member. But it could also mean that the ratio \(13 \colon 1\) was just slightly rounded, which is also likely. For example, say there are \(289\) faculty — then the real student to faculty ratio would be \(3752 \colon 289\), which cannot be reduced. This ratio, \(3752\) to \(289\), would not be a good ratio to put on the website, because it's hard to understand. The ratio \(13 \colon 1\), while it may have been rounded just slightly, provides a better picture of what class sizes at Western look like.

Now, in the previous example, you may have seen a quicker way to solve this problem using proportions. In general, if you find a way to solve a problem that works for you, as long as you get the same numerical answer, you can use that method. We will cover proportions in the next section. In this section, we are choosing to focus on equivalent ratios as a method for problem-solving.

Let's see one more example.

Example \(\PageIndex{4}\)

In a given afternoon, a librarian checks out \(52\) total books. Of those, \(24\) are fiction books. What is the ratio, in lowest terms, of non-fiction books to fiction books checked out of the library that afternoon?

In a given afternoon, a librarian checks out 52 total books. Of those, 24 are fiction books. What is the ratio, in lowest terms, of non-fiction books to fiction books checked out of the library that afternoon?

In this problem we need to know that library books are either fiction or non-fiction books. Therefore, the number of non-fiction books can be found by calculating \(\underset{\text{total books}}{52} - \underset{\text{fiction books}}{24} = \underset{\text{non-fiction books}}{28}\)

Thus, the ratio of non-fiction books to fiction books is \(28 \colon 24\). We see that both \(28\) and \(24\) have a factor of \(4\), so when we divide both parts of the ratio by \(4\), we get a ratio of \(7 \colon 6\). That ratio is in lowest terms, so the answer is: There was a ratio of \(7 \colon 6\) non-fiction books to fiction books checked out of the library that afternoon. 

Two Important Real-World Ratios

The remainder of this section is dedicated to two real-world ratios that you will likely encounter at some point in your life. They are:

• Your cholesterol ratio
• Your debt-to-income ratio

Before we proceed, you should know: the person writing these notes is neither a medical doctor nor a financial professional. The information in this section should not replace the advice of an actual physician or financial planner! The guidelines outlined below are based on publicly available information, and sources are cited where appropriate. In some cases some simplifications have been made for the sake of clarity.

First, we'll study the cholesterol ratio, which is used to indicate risk of heart attack and coronary disease by doctors. Cholesterol is a fat-like substance that's found in many common foods. There are two main types of cholesterol:

• HDL , or high-density lipoprotein , which is sometimes called "good cholesterol." HDL carries other cholesterol away from your arteries and to your liver, thereby reducing the risk of clogged arteries. HDL is found in foods like avocado, nuts, and vegetable-based oils. Smoking can also decrease HDL levels.
• LDL , or low-density lipoprotein , which is sometimes called "bad cholesterol." LDL is the type of cholesterol that sticks to the sides of your arteries, thereby increasing the risk of clogged arteries. LDL is found in foods with lots of saturated and trans fats, like butter, red meat, and fried foods. Smoking can also increase LDL levels.

You can get your own cholesterol tested by requesting a lipoprotein panel from a physician. In general, it is ideal to have an LDL level below 100 milligrams per deciliter (mg/dL) and an HDL level above 45 mg/dL. Additionally, your total cholesterol should be below 200 mg/dL. Various demographic factors affect your personal ideal levels.

However, since the two types of cholesterol interact, doctors will often monitor a number known as your cholesterol ratio . This is calculated in the following way:

\[\underset{\text{HDL}}{45} + \underset{\text{LDL}}{110} = \underset{\text{total cholesterol}}{155}\]

where the "total cholesterol" is calculated as

\[\text{cholesterol ratio} = \frac{\text{total cholesterol}}{\text{HDL}} = \frac{155}{45} \approx 3.44\]

Since HDL is good cholesterol, and LDL is bad cholesterol, a low cholesterol ratio is an indicator of better health and lower heart attack risk. Mathematically, we want the top of the fraction, LDL + HDL, to be relatively low compared to the bottom, which is just HDL. In general, the ideal ratio is 3.5 or lower, and should be kept below 5 .

Note that the ratio has no units — it is simply a number. As with LDL and HDL recommendations, various demographic factors affect the exact recommended levels. You can find more information about this here .

Example \(\PageIndex{5}\)

You receive the results of a lipoprotein panel from your doctor. Your LDL is 110 mg/dL, and your HDL is 45 mg/dL. What is your cholesterol ratio, and what does this indicate about your risk for heart disease? Round numerical answers to two decimal places.

To calculate your cholesterol ratio, we need to know the total cholesterol. We calculate this as follows: \[\underset{\text{HDL}}{45} + \underset{\text{LDL}}{110} = \underset{\text{total cholesterol}}{155}\]

Now we calculate your cholesterol ratio as follows \[\text{cholesterol ratio} = \frac{\text{total cholesterol}}{\text{HDL}} = \frac{155}{45} \approx 3.44\]

This ratio represents a fairly low risk for heart disease, since it is below 3.5. Additionally, your total cholesterol is below 200 mg/dL, which is good. However, the LDL number is a bit high — ideally, it should be below 100 mg/dL. 

The last ratio we'll study is the debt-to-income ratio, also called DTI . This ratio is used frequently by lenders to determine if someone is eligible to borrow money for a large purchase or credit line. This is not be confused with a person's credit score. 

To calculate a person's debt-to-income ratio, we use the following formula:

\[\text{DTI }= \text{debt-to-income ratio} = \frac{\text{total monthly debt payments}}{\text{monthly gross income}}\]

Let's examine the two parts of the fraction. A person's monthly gross income is the amount of money they make in a month before any taxes or deductions, such as federal tax, state tax, or Social Security tax are taken out. This amount can be found on a pay stub, and it's likely higher than what you actually take home in your paycheck.

A person's total monthly debt payments can be calculated by adding up the debt payments they make each month to debts they have. Debt payments include things like:

• House payment (mortgage) or rent payments
• Student loan payments
• Auto loan payments
• Credit card payments
• Child support or alimony payments
• Any other type of debt: personal loan, medical loan, etc.

Other monthly payments that you might make are typically not considered debt. For example, groceries, utilities, subscriptions, and gas do not count towards your total monthly debt payments

It's important to note that different lenders use slightly different definitions of what counts as debt. The list above is intended to be as general as possible, and is what we will use in this class; however, you may encounter slightly different criteria when you actually apply for a loan. For more information, visit a financial institution's website such as this one .

Once the debt-to-income ratio is calculated, it is compared to a benchmark number. In practice, that benchmark number varies, but is typically around .36, which is what we will use in this class. If your DTI is less than .36, that means you are a good candidate for lending — your debts are relatively low compared to your income. If your DTI is more than .36, that means you are a riskier candidate for lending, because your debts are already somewhat high compared to your income.

In general, you want to keep your debt-to-income ratio as low as possible. However, some lenders accept a DTI of up to 50%, depending on the type of loan.

Example \(\PageIndex{6}\)

You currently make \(\$2800\) gross income per month. Your rent costs \(\$550\) per month, your monthly minimum credit card payments are \(\$300\), you spend \(\$350\) per month on groceries, and your car payment is \(\$150\) per month. What is your debt-to-income ratio? If you applied for a home loan, do you think you would be approved? Why or why not? 

First, we add up all of the monthly debt payments. Be careful -- not every monthly expense is a debt payment! You will need to read carefully and consult the list of debts above to tell what expenses are and aren't debts. The debts in this case are the rent, credit card payments, and car payments. The groceries are not a debt payment, so we don't include them. We add the debt payments to find the total monthly debt payments: \[\underset{\text{rent}}{\$550} + \underset{\text{credit cards}}{\$300} + \underset{\text{car loan}}{\$150} = 1000 = \text{ total monthly debt payments}\]

Now, to find the DTI, we calculate \[{DTI }= \frac{\text{total monthly debt payments}}{\text{Monthly gross income}} = \frac{\$1000}{\$2800} \approx .357\]

We see that this DTI is just slightly less than the ideal number, .36. That means that you're likely a good candidate for a home loan, but close to being a risky candidate. You are fairly likely to be approved for a home loan.

Make sure to include supporting work for all answers

• Write \(6 \colon 11\) in two other ways.
• Write three equivalent ratios.
• Is the ratio \(6\colon 11\) in lowest terms? Explain why or why not in a complete sentence.
• In a given pond, there are 22 rock fish for every 121 minnows. Express the ratio of minnows to rock fish in lowest terms.
• The ratio of the amount of food that my cat Jade eats to the amount of food that my cat Poe eats is \(3 \colon 2\). If Jade eats 6 ounces of food, how many ounces of food will Poe eat? (Your answer should be a whole number.)
• Sourdough bread uses a 5 to 4 ratio of flour to sourdough starter. If you have 10 cups of flour, how much sourdough starter should you use?
• Elizabeth's total cholesterol is 182 and her LDL is 128. What is her cholesterol ratio? How might you evaluate her overall heart health in 1-2 sentences?
• Mark's gross monthly income is $2300. His rent is $575, his monthly car payment is $120, his utilities cost $300 per month, his student loan payment is $63 per month, and he spends $300 per month on groceries. What is his debt-to-income ratio? If he applied for a mortgage, do you think he would be approved? Why or why not?
• Do a bit of research and write a paragraph (4-5 sentences) about what a person's credit score is, including how it is calculated and how it affects one's chances of being approved to borrow money.

Maths with Mum

Be your child's best tutor

Solving Ratio Problems

• We add the parts of the ratio to find the total number of parts.
• There are 2 + 3 = 5 parts in the ratio in total.
• To find the value of one part we divide the total amount by the total number of parts.
• 50 ÷ 5 = 10.
• We multiply the ratio by the value of each part.
• 2:3 multiplied by 10 gives us 20:30.
• The 50 counters are shared into 20 counters to 30 counters.

• 2 + 3 = 5 and so there are 5 parts in the ratio in total.
• We divide by this total number of parts to find the value of each part.
• We multiply the original ratio by the value of each part.
• We have 20:30.

• Sharing in a Ratio: Part 1

Ratio Problems: Worksheets and Answers

How to Solve Ratio Problems

Share this:

• Click to share on Twitter (Opens in new window)
• Click to share on Facebook (Opens in new window)
• Click to share on WhatsApp (Opens in new window)
• Click to share on Pinterest (Opens in new window)
• Click to email a link to a friend (Opens in new window)
• Click to print (Opens in new window)
• Click to share on Tumblr (Opens in new window)
• Click to share on Pocket (Opens in new window)
• Click to share on Telegram (Opens in new window)
• Click to share on Skype (Opens in new window)

A ratio compares values .

A ratio says how much of one thing there is compared to another thing.

Ratios can be shown in different ways:

A ratio can be scaled up:

Try it Yourself

Using ratios.

The trick with ratios is to always multiply or divide the numbers by the same value .

Example: A Recipe for pancakes uses 3 cups of flour and 2 cups of milk.

So the ratio of flour to milk is 3 : 2

To make pancakes for a LOT of people we might need 4 times the quantity, so we multiply the numbers by 4:

3 ×4 : 2 ×4 = 12 : 8

In other words, 12 cups of flour and 8 cups of milk .

The ratio is still the same, so the pancakes should be just as yummy.

"Part-to-Part" and "Part-to-Whole" Ratios

The examples so far have been "part-to-part" (comparing one part to another part).

But a ratio can also show a part compared to the whole lot .

Example: There are 5 pups, 2 are boys, and 3 are girls

Part-to-Part:

The ratio of boys to girls is 2:3 or 2 / 3

The ratio of girls to boys is 3:2 or 3 / 2

Part-to-Whole:

The ratio of boys to all pups is 2:5 or 2 / 5

The ratio of girls to all pups is 3:5 or 3 / 5

Try It Yourself

We can use ratios to scale drawings up or down (by multiplying or dividing).

Example: To draw a horse at 1/10th normal size, multiply all sizes by 1/10th

This horse in real life is 1500 mm high and 2000 mm long, so the ratio of its height to length is

1500 : 2000

What is that ratio when we draw it at 1/10th normal size?

We can make any reduction/enlargement we want that way.

"I must have big feet, my foot is nearly as long as my Mom's!"

But then she thought to measure heights, and found she is 133cm tall, and her Mom is 152cm tall.

In a table this is:

The "foot-to-height" ratio in fraction style is:

We can simplify those fractions like this:

And we get this (please check that the calcs are correct):

"Oh!" she said, "the Ratios are the same".

"So my foot is only as big as it should be for my height, and is not really too big."

You can practice your ratio skills by Making Some Chocolate Crispies

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• Mathematics

How to Calculate Ratios

Last Updated: January 29, 2024 References

This article was co-authored by Grace Imson, MA . Grace Imson is a math teacher with over 40 years of teaching experience. Grace is currently a math instructor at the City College of San Francisco and was previously in the Math Department at Saint Louis University. She has taught math at the elementary, middle, high school, and college levels. She has an MA in Education, specializing in Administration and Supervision from Saint Louis University. This article has been viewed 3,126,695 times.

Ratios are mathematical expressions that compare two or more numbers. They can compare absolute quantities and amounts or can be used to compare portions of a larger whole. Ratios can be calculated and written in several different ways, but the principles guiding the use of ratios are universal to all.

Practice Problems

Understanding Ratios

• Ratios can be used to show the relation between any quantities, even if one is not directly tied to the other (as they would be in a recipe). For example, if there are five girls and ten boys in a class, the ratio of girls to boys is 5 to 10. Neither quantity is dependent on or tied to the other, and would change if anyone left or new students came in. The ratio merely compares the quantities.

• You will commonly see ratios represented using words (as above). Because they are used so commonly and in such a variety of ways, if you find yourself working outside of mathematic or scientific fields, this may the most common form of ratio you will see.
• Ratios are frequently expressed using a colon. When comparing two numbers in a ratio, you'll use one colon (as in 7 : 13). When you're comparing more than two numbers, you'll put a colon between each set of numbers in succession (as in 10 : 2 : 23). In our classroom example, we might compare the number of boys to the number of girls with the ratio 5 girls : 10 boys. We can simply express the ratio as 5 : 10.
• Ratios are also sometimes expressed using fractional notation. In the case of the classroom, the 5 girls and 10 boys would be shown simply as 5/10. That said, it shouldn't be read out loud the same as a fraction, and you need to keep in mind that the numbers do not represent a portion of a whole.

Using Ratios

• In the classroom example above, 5 girls to 10 boys (5 : 10), both sides of the ratio have a factor of 5. Divide both sides by 5 (the greatest common factor) to get 1 girl to 2 boys (or 1 : 2). However, we should keep the original quantities in mind, even when using this reduced ratio. There are not 3 total students in the class, but 15. The reduced ratio just compares the relationship between the number of boys and girls. There are 2 boys for every girl, not exactly 2 boys and 1 girl.
• Some ratios cannot be reduced. For example, 3 : 56 cannot be reduced because the two numbers share no common factors - 3 is a prime number, and 56 is not divisible by 3.

• For example, a baker needs to triple the size of a cake recipe. If the normal ratio of flour to sugar is 2 to 1 (2 : 1), then both numbers must be increased by a factor of three. The appropriate quantities for the recipe are now 6 cups of flour to 3 cups of sugar (6 : 3).
• The same process can be reversed. If the baker needed only one-half of the normal recipe, both quantities could be multiplied by 1/2 (or divided by two). The result would be 1 cup of flour to 1/2 (0.5) cup of sugar.

• For example, let's say we have a small group of students containing 2 boys and 5 girls. If we were to maintain this proportion of boys to girls, how many boys would be in a class that contained 20 girls? To solve, first, let's make two ratios, one with our unknown variables: 2 boys : 5 girls = x boys : 20 girls. If we convert these ratios to their fraction forms, we get 2/5 and x/20. If you cross multiply, you are left with 5x=40, and you can solve by dividing both figures by 5. The final solution is x=8.

Grace Imson, MA

Look at the order of terms to figure out the numerator and denominator in a word problem. The first term is usually the numerator, and the second is usually the denominator. For example, if a problem asks for the ratio of the length of an item to its width, the length will be the numerator, and width will be the denominator.

Catching Mistakes

• Wrong method: "8 - 4 = 4, so I added 4 potatoes to the recipe. That means I should take the 5 carrots and add 4 to that too... wait! That's not how ratios work. I'll try again."
• Right method: "8 ÷ 4 = 2, so I multiplied the number of potatoes by 2. That means I should multiply the 5 carrots by 2 as well. 5 x 2 = 10, so I want 10 carrots total in the new recipe."

• A dragon has 500 grams of gold and 10 kilograms of silver. What is the ratio of gold to silver in the dragon's hoard?

• The dragon has 500 grams of gold and 10,000 grams of silver.

• Example problem: If you have six boxes, and in every three boxes there are nine marbles, how many marbles do you have?

One common problem is knowing which number to use as a numerator. In a word problem, the first term stated is usually the numerator and the second term stated is usually the denominator. If you want the ratio of the length of an item to the width, length becomes your numerator and width becomes your denominator.

Community Q&A

You Might Also Like

• ↑ http://www.virtualnerd.com/common-core/grade-6/6_RP-ratios-proportional-relationships/A
• ↑ http://www.purplemath.com/modules/ratio.htm
• ↑ http://www.helpwithfractions.com/math-homework-helper/least-common-denominator/
• ↑ http://www.mathplanet.com/education/algebra-1/how-to-solve-linear-equations/ratios-and-proportions-and-how-to-solve-them
• ↑ http://www.math.com/school/subject1/lessons/S1U2L2DP.html

About This Article

To calculate a ratio, start by determining which 2 quantities are being compared to each other. For example, if you wanted to know the ratio of girls to boys in a class where there are 5 girls and 10 boys, 5 and 10 would be the quantities you're comparing. Then, put a colon or the word "to" between the numbers to express them as a ratio. In this example, you'd write "5 to 10" or "5:10." Finally, simplify the ratio if possible by dividing both numbers by the greatest common factor. To learn how to solve equations and word problems with ratios, scroll down! Did this summary help you? Yes No

• Send fan mail to authors

Reader Success Stories

Stew Jackson

Feb 9, 2021

Did this article help you?

Maria Bustos

May 3, 2021

Lynn Robinson

Apr 17, 2017

Mar 15, 2019

Dec 11, 2021

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Level up your tech skills and stay ahead of the curve

Ratio Math Problems - Three Term Ratios

In these lessons, we will learn how to solve ratio word problems that involve three terms.

Related Pages Two-Term Ratio Word Problems More Ratio Word Problems Math Word Problems More Algebra Lessons

Ratio problems are word problems that use ratios to relate the different items in the question.

Ratio problems: Three-term Ratios

Example 1: A special cereal mixture contains rice, wheat and corn in the ratio of 2:3:5. If a bag of the mixture contains 3 pounds of rice, how much corn does it contain?

Step 2: Solve the equation: Cross Multiply

2 × x = 3 × 5 2x = 15

Answer: The mixture contains 7.5 pounds of corn.

Example 2: Clothing store A sells T-shirts in only three colors: red, blue and green. The colors are in the ratio of 3 to 4 to 5. If the store has 20 blue T-shirts, how many T-shirts does it have altogether?

Solution: Step 1: Assign variables: Let x = red shirts y = green shirts

Step 2: Solve the equation: Cross Multiply both equations 3 × 20 = x × 4 60 = 4x x = 15

5 × 20 = y × 4 100 = 4y y = 25

The total number of shirts would be 15 + 25 + 20 = 60

Answer: There are 60 shirts.

How to solve Ratio Word Problems with three terms?

Example: A piece of string that is 63 inches long is cut into 3 parts such that the lengths of the parts of the string are in the ratio of 5 to 6 to 10. Find the lengths of the 3 parts.

How to solve Two Term and Three Term Ratio Problems?

A Ratio compares two things that have the same units A Part to Part Ratio compares one thing to another thing A Part to Total (whole) Ratio compares one thing to the total number

Example: In a class of 30 students, there are 18 girls and 12 boys. What is the ratio of boys to girls? What is the ratio of girls to boys? What is the ratio of girls to total?

We can have a three term ratio of red to blue to green marbles.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

How do we solve ratio problems?

If you're seeing this message, it means we're having trouble loading external resources on our website.

If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.

To log in and use all the features of Khan Academy, please enable JavaScript in your browser.

Course: 6th grade   >   Unit 1

• Ratios on coordinate plane
• Ratios and measurement
• Ratios and units of measurement

Part to whole ratio word problem using tables

• Part-part-whole ratios

Want to join the conversation?

• Upvote Button navigates to signup page
• Downvote Button navigates to signup page
• Flag Button navigates to signup page

Video transcript

• Math Article
• Ratios And Proportion

Ratios and Proportion

Ratio and Proportion are explained majorly based on fractions. When a fraction is represented in the form of a:b, then it is a ratio whereas a proportion states that two ratios are equal. Here, a and b are any two integers.  The ratio and proportion are the two important concepts, and it is the foundation to understand the various concepts in mathematics as well as in science.

In our daily life, we use the concept of ratio and proportion such as in business while dealing with money or while cooking any dish, etc. Sometimes, students get confused with the concept of ratio and proportion. In this article, the students get a clear vision of these two concepts with more solved examples and problems.

For example, ⅘ is a ratio and the proportion statement is 20/25 = ⅘. If we solve this proportional statement, we get:

20 x 5 = 25 x 4

Check: Ratio and Proportion PDF

Therefore, the ratio defines the relationship between two quantities such as a:b, where b is not equal to 0. Example: The ratio of 2 to 4 is represented as 2:4 = 1:2. And the statement is said to be in proportion here. The application of proportion can be seen in direct proportion .

What is Ratio and Proportion in Maths?

The definition of ratio and proportion is described here in this section. Both concepts are an important part of Mathematics. In real life also, you may find a lot of examples such as the rate of speed (distance/time) or price (rupees/meter) of a material, etc, where the concept of the ratio is highlighted.

Proportion is an equation that defines that the two given ratios are equivalent to each other. For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.

Let us now learn Maths ratio and proportion concept one by one.

Ratio Meaning

In certain situations, the comparison of two quantities by the method of division is very efficient. We can say that the comparison or simplified form of two quantities of the same kind is referred to as a ratio. This relation gives us how many times one quantity is equal to the other quantity. In simple words, the ratio is the number that can be used to express one quantity as a fraction of the other ones.

The two numbers in a ratio can only be compared when they have the same unit. We make use of ratios to compare two things. The sign used to denote a ratio is ‘:’.

A ratio can be written as a fraction, say 2/5. We happen to see various comparisons or say ratios in our daily life.

Hence, the ratio can be represented in three different forms, such as:

Key Points to Remember: 

• The ratio should exist between the quantities of the same kind
• While comparing two things, the units should be similar
• There should be significant order of terms
• The comparison of two ratios can be performed, if the ratios are equivalent like the fractions

Definition of Proportion

Proportion is an equation that defines that the two given ratios are equivalent to each other. In other words, the proportion states the equality of the two fractions or the ratios. In proportion, if two sets of given numbers are increasing or decreasing in the same ratio, then the ratios are said to be directly proportional to each other.

For example, the time taken by train to cover 100km per hour is equal to the time taken by it to cover the distance of 500km for 5 hours. Such as 100km/hr = 500km/5hrs.

Ratio and proportions are said to be faces of the same coin. When two ratios are equal in value, then they are said to be in proportion . In simple words, it compares two ratios. Proportions are denoted by the symbol  ‘::’ or ‘=’.

The proportion can be classified into the following categories, such as:

Direct Proportion

Inverse proportion, continued proportion.

Now, let us discuss all these methods in brief:

The direct proportion describes the relationship between two quantities, in which the increases in one quantity, there is an increase in the other quantity also. Similarly, if one quantity decreases, the other quantity also decreases. Hence, if “a” and “b” are two quantities, then the direction proportion is written as a∝b.

The inverse proportion describes the relationship between two quantities in which an increase in one quantity leads to a decrease in the other quantity. Similarly, if there is a decrease in one quantity, there is an increase in the other quantity. Therefore, the inverse proportion of two quantities, say “a” and “b” is represented by a∝(1/b).

Consider two ratios to be a: b and c: d .

Then in order to find the continued proportion for the two given ratio terms, we convert the means to a single term/number. This would, in general, be the LCM of means.

For the given ratio, the LCM of b & c will be bc.

Thus, multiplying the first ratio by c and the second ratio by b, we have

First ratio- ca:bc

Second ratio- bc: bd

Thus, the continued proportion can be written in the form of ca: bc: bd

Ratio and Proportion Formula

Now, let us learn the Maths ratio and proportion formulas here.

Ratio Formula

Assume that, we have two quantities (or two numbers or two entities) and we have to find the ratio of these two, then the formula for ratio is defined as;

where a and b could be any two quantities .

Here, “a” is called the first term or antecedent , and “b” is called the second term or consequent .

Example: In ratio 4:9, is represented by 4/9, where 4 is antecedent and 9 is consequent.

If we multiply and divide each term of ratio by the same number (non-zero), it doesn’t affect the ratio.

Example: 4:9 = 8:18 = 12:27

Also, read:    Ratio Formula

Proportion Formula

Now, let us assume that, in proportion, the two ratios are a:b & c:d. The two terms ‘b’ and ‘c’ are called  ‘means or mean term,’ whereas the terms ‘a’ and ‘d’ are known as ‘ extremes or extreme terms.’

Example:  Let us consider one more example of a number of students in a classroom. Our first ratio of the number of girls to boys is 3:5 and that of the other is 4:8, then the proportion can be written as:

3 : 5 ::  4 : 8 or 3/5 = 4/8

Here, 3 & 8 are the extremes, while 5 & 4 are the means.

Note: The ratio value does not affect when the same non-zero number is multiplied or divided on each term.

Important Properties of Proportion

The following are the important properties of proportion:

• Addendo – If a : b = c : d, then a + c : b + d
• Subtrahendo – If a : b = c : d, then a – c : b – d
• Dividendo – If a : b = c : d, then a – b : b = c – d : d
• Componendo – If a : b = c : d, then a + b : b = c+d : d
• Alternendo – If a : b = c : d, then a : c = b: d
• Invertendo – If a : b = c : d, then b : a = d : c
• Componendo and dividendo – If a : b = c : d, then a + b : a – b = c + d : c – d

Difference Between Ratio and Proportion

To understand the concept of ratio and proportion, go through the difference between ratio and proportion given here.

Fourth, Third and Mean Proportional

If a : b = c : d, then:

• d is called the fourth proportional to a, b, c.
• c is called the third proportion to a and b.
• Mean proportional between a and b is √(ab).

Comparison of Ratios

If (a:b)>(c:d) = (a/b>c/d)

The compounded ratio of the ratios: (a : b), (c : d), (e : f) is (ace : bdf).

Duplicate Ratios

If a:b is a ratio, then:

• a 2 :b 2  is a duplicate ratio
• √a:√b is the sub-duplicate ratio
• a 3 :b 3 is a triplicate ratio

Ratio and Proportion Tricks

Let us learn here some rules and tricks to solve problems based on ratio and proportion topics.

• If u/v = x/y, then uy = vx
• If u/v = x/y, then u/x = v/y
• If u/v = x/y, then v/u = y/x
• If u/v = x/y, then (u+v)/v = (x+y)/y
• If u/v = x/y, then (u-v)/v = (x-y)/y
• If u/v = x/y, then (u+v)/ (u-v) = (x+y)/(x-y), which is known as componendo -Dividendo Rule
• If a/(b+c) = b/(c+a) = c/(a+b) and a+b+ c ≠0, then a =b = c

Ratio and Proportion Summary

• Ratio defines the relationship between the quantities of two or more objects. It is used to compare the quantities of the same kind.
• If two or more ratios are equal, then it is said to be in proportion.
• The proportion can be represented in two different ways. Either it can be represented using an equal sign or by using a colon symbol. (i.e) a:b = c:d or a:b :: c:d
• If we multiply or divide each term of the ratio by the same number, it does not affect the ratio.
• For any three quantities, the quantities are said to be in continued proportion, if the ratio between the first and second quantity is equal to the ratio between the second and third quantity.
• For any four quantities, they are said to be in continued proportion, if the ratio between the first and second quantities is equal to the ratio between the third and fourth quantities

Ratio And Proportion Examples

Example 1: 

Are the ratios 4:5 and 8:10 said to be in Proportion?

4:5= 4/5 = 0.8 and 8: 10= 8/10= 0.8

Since both the ratios are equal, they are said to be in proportion.

Are the two ratios 8:10 and 7:10 in proportion?

8:10= 8/10= 0.8 and 7:10= 7/10= 0.7

Since both the ratios are not equal, they are not in proportion.

Example 3: 

Given ratio are-

Find a: b: c.

Multiplying the first ratio by 5, second by 3 and third by 6, we have

a:b = 10: 15

b:c = 15 : 6

c:d = 6 : 24

In the ratio’s above, all the mean terms are equal, thus

a:b:c:d = 10:15:6:24

Check whether the following statements are true or false.

a] 12 : 18 = 28 : 56

b] 25 people : 130 people = 15kg : 78kg

The given statement is false.

12 : 18 = 12 / 18 = 2 / 3 = 2 : 3

28 : 56 = 28 / 56 = 1 / 2 = 1 : 2

They are unequal.

b] 25 persons : 130 persons = 15kg : 78kg

The given statement is true.

25 people : 130 people = 5: 26

15kg : 78kg = 5: 26

They are equal.

The earnings of Rohan is 12000 rupees every month and Anish is 191520 per year. If the monthly expenses of every person are around 9960 rupees. Find the ratio of the savings.

Savings of Rohan per month = Rs (12000-9960) = Rs. 2040

Yearly income of Anish = Rs. 191520

Hence, the monthly income of Anish = Rs. 191520/12 = Rs. 15960.

So, the savings of Anish per month = Rs (15960 – 9960) = Rs. 6000

Thus, the ratio of savings of Rohan and Anish is Rs. 2040: Rs.6000 = 17: 50.

Twenty tons of iron is Rs. 600000 (six lakhs). What is the cost of 560 kilograms of iron?

1 ton = 1000 kg 20 tons = 20000 kg The cost of 20000 kg iron = Rs. 600000 The cost of 1 kg iron = Rs{600000}/ {20000} = Rs. 30 The cost of 560 kg iron = Rs 30 × 560 = Rs 16800

The dimensions of the rectangular field are given. The length and breadth of the rectangular field are 50 meters and 15 meters. What is the ratio of the length and breadth of the field?

Length of the rectangular field = 50 m

Breadth of the rectangular field = 15 m

Hence, the ratio of length to breadth = 50: 15

⇒ 50: 15 = 10: 3.

Thus, the ratio of length and breadth of the rectangular field is 10:3.

Obtain a ratio of 90 centimetres to 1.5 meters.

The given two quantities are not in the same units.

Convert them into the same units.

1.5 m = 1.5 × 100 = 150 cm

Hence, the required ratio is 90 cm: 150 cm

⇒ 90: 150 = 3: 5

Therefore, the ratio of 90 centimetres to 1.5 meters is 3: 5.

There exists 45 people in an office. Out of which female employees are 25 and the remaining are male employees. Find the ratio of

a] The count of females to males.

b] The count of males to females.

Count of females = 25

Total count of employees = 45

Count of males = 45 – 25 = 20

The ratio of the count of females to the count of males

The count of males to the count of females

Example 10:

Write two equivalent ratios of 6: 4.

Given Ratio : 6: 4, which is equal to 6/4.

Multiplying or dividing the same numbers on both numerator and denominator, we will get the equivalent ratio.

⇒(6×2)/(4×2) = 12/8 = 12: 8

⇒(6÷2)/(4÷2) = 3/2 = 3: 2

Therefore, the two equivalent ratios of 6: 4 are 3: 2 and 12: 8

Example 11 : 

Out of the total students in a class, if the number of boys is 5 and the number of girls is 3, then find the ratio between girls and boys.

The ratio between girls and boys can be written as 3:5 (Girls: Boys). The ratio can also be written in the form of factor like 3/5.

Example 12: 

Two numbers are in the ratio 2 : 3. If the sum of numbers is 60, find the numbers.

Given, 2/3 is the ratio of any two numbers.

Let the two numbers be 2x and 3x.

As per the given question, the sum of these two numbers = 60

So, 2x + 3x = 60

Hence, the two numbers are;

2x = 2 x 12 = 24

3x = 3 x 12 = 36

24 and 36 are the required numbers.

Maths ratio and proportion are used to solve many real-world problems. Register with BYJU’S – The Learning App and get solutions for many difficult questions in easy methodology and followed by the step-by-step procedure.

Frequently Asked Questions on Ratios and Proportion

What is the ratio give an example., what is a proportion give example, how to solve proportions with examples, what is the concept of ratios, what are the two different types of proportions.

The two different types of proportions are: Direct Proportion Inverse Proportion

Can we express ratio in terms of fractions?

Yes, we can express ratio in terms of fractions. For example, 3: 4 can be expressed as 3/4.

What is the formula for ratio and proportion?

The formula for ratio is: x:y ⇒ x/y, where x is the first term and y is the second term. The formula for proportion is: p: q :: r : s ⇒ p/q = r/s, Where p and r are the first term in the first and second ratio q and s are the second term and in the first and second ratio.

Find the means and extremes of the proportion 1: 2 :: 3: 4.

In the given proportion 1: 2 :: 3: 4, Means are 2 and 3 Extremes are 1 and 4.

Put your understanding of this concept to test by answering a few MCQs. Click ‘Start Quiz’ to begin!

Select the correct answer and click on the “Finish” button Check your score and answers at the end of the quiz

Visit BYJU’S for all Maths related queries and study materials

Your result is as below

Request OTP on Voice Call

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Post My Comment

Very helpful

• Share Share

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

• Parallelogram
• Quadrilateral
• Parallelepiped
• Tetrahedron
• Dodecahedron
• Fraction Calculator
• Mixed Fraction Calculator
• Greatest Common Factor Calulator
• Decimal to Fraction Calculator
• Whole Numbers
• Rational Numbers
• Place Value
• Irrational Numbers
• Natural Numbers
• Binary Operation
• Numerator and Denominator
• Order of Operations (PEMDAS)
• Scientific Notation

Last modified on August 3rd, 2023

Ratio Word Problems

Here, we will learn to do some practical word problems involving ratios.

Amelia and Mary share $40 in a ratio of 2:3. How much do they get separately?

There is a total reward of $40 given.  Let Amelia get = 2x and Mary get = 3x Then, 2x + 3x = 40 Now, we solve for x => 5x = 40 => x = 8 Thus, Amelia gets = 2x = 2 × 8 = $16 Mary gets = 3x = 3 × 8 = $24

In a bag of blue and red marbles, the ratio of blue marbles to red marbles is 3:4. If the bag contains 120 green marbles, how many blue marbles are there?

Let the total number of blue marbles be x Thus, ${\dfrac{3}{4}=\dfrac{x}{120}}$ x = ${\dfrac{3\times 120}{4}}$ x = 90 So, there are 90 blue marbles in the bag.

Gregory weighs 75.7 kg. If he decreases his weight in the ratio of 5:4, find his reduced weight.

Let the decreased weight of Gregory be = x kg Thus, 5x = 75.7 x = \dfrac{75\cdot 7}{5} = 15.14 Thus his reduced weight is 4 × 15.14 = 60.56 kg

A recipe requires butter and sugar to be in the ratio of 2:3. If we require 8 cups of butter, find how many cups of sugar are required. Write the equivalent fraction.

Thus, for every 2 cups of butter, we use 3 cups of sugar Here we are using 8 cups of butter, or 4 times as much So you need to multiply the amount of sugar by 4 3 × 4 = 12 So, we need to use 12 cups of sugar Thus, the equivalent fraction is ${\dfrac{2}{3}=\dfrac{8}{12}}$

Jerry has 16 students in his class, of which 10 are girls. Write the ratio of girls to boys in his class. Reduce your answer to its simplest form.

Total number of students = 16 Number of girls = 10 Number of boys = 16 – 10 = 6 Thus the ratio of girls to boys is ${\dfrac{10}{6}=\dfrac{5}{3}}$

A bag containing chocolates is divided into a ratio of 5:7. If the larger part contains 84 chocolates, find the total number of chocolates in the bag.

Let the total number of chocolates be x

Then the two parts are:

${\dfrac{5x}{5+7}}$ and ${\dfrac{7x}{5+7}}$

${\dfrac{7x}{5+7}}$ = 84

=> ${\dfrac{7x}{12}}$ = 84

Thus, the total number of chocolates that were present in the bag was 144

Leave a comment Cancel reply

Your email address will not be published. Required fields are marked *

Save my name, email, and website in this browser for the next time I comment.

• Privacy Policy
• Trigonometry

Join Our Newsletter

© 2024 Mathmonks.com . All rights reserved. Reproduction in whole or in part without permission is prohibited.