quadratic equation solver with imaginary numbers

Quadratic Formula Calculator & Solver

Calculator for solutions to any quadratic equation..

The calculator uses the quadratic formula to find solutions to any quadratic equation .

The quadratic formula calculator below will solve any quadratic equation that you type in. Simply type in a number for 'a', 'b' and 'c' then hit the 'solve' button.

Quadratic Formula Calculator and Solver

The Discriminant

The Actual Solutions

Parabola Animated Gifs

More Quadratic Gifs

The calculator on this page shows how the quadratic formula operates, but if you have access to a graphing calculator you should be able to solve quadratic equations, even ones with imaginary solutions.

• Step 1) Most graphing calculators like the TI- 83 and others allow you to set the "Mode" to "a + bi" (Just click on 'mode' and select 'a+bi').
• If you can set your calculator's mode to a + bi you should be able to even calculate imaginary solutions.
• The rest of the steps just involve typing in a,b and c. Make sure that you divide the entire numerator by 2a, just use parentheses.
• Quadratic formula worksheets (several free printable pdfs with answer keys on the quadratic formula)

Create the graph of any Parabola

Save Graph as Image to your desktop

• Quadratic Equations
• Other Free Math Calculators
• All roots calculated

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Wolfram|Alpha Widgets Overview Tour Gallery Sign In

Share this page.

• StumbleUpon
• Google Buzz

Output Type

Output width, output height.

To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.

To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:

Save to My Widgets

Build a new widget.

We appreciate your interest in Wolfram|Alpha and will be in touch soon.

Quadratic Equation Solver

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Step-By-Step Example

Example (click to try), choose your method, solve by factoring.

Example: 3x^2-2x-1=0

Complete The Square

Example: 3x^2-2x-1=0 (After you click the example, change the Method to 'Solve By Completing the Square'.)

Take the Square Root

Example: 2x^2=18

Quadratic Formula

Example: 4x^2-2x-1=0

About quadratic equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Quadratic Equation Solver »

Quadratic Formula Calculator

Enter the equation you want to solve using the quadratic formula.

The Quadratic Formula Calculator finds solutions to quadratic equations with real coefficients. For equations with real solutions, you can use the graphing tool to visualize the solutions.

Quadratic Formula : x = − b ± b 2 − 4 a c 2 a

Click the blue arrow to submit. Choose "Solve Using the Quadratic Formula" from the topic selector and click to see the result in our Algebra Calculator !

Solve Using the Quadratic Formula Apply the Quadratic Formula

Popular Problems

Solve Using the Quadratic Formula x 2 + 5 x + 6 = 0 Solve Using the Quadratic Formula x 2 - 9 = 0 Solve Using the Quadratic Formula 5 x 2 - 7 x - 3 = 0 Apply the Quadratic Formula x 2 - 14 x + 49 Apply the Quadratic Formula x 2 - 18 x - 4

Please ensure that your password is at least 8 characters and contains each of the following:

• a special character: @$#!%*?&

Video Crash Courses

Junior Math

Math Essentials

Tutor-on-Demand

Encyclopedia

Digital Tools

How to Solve Quadratic Equations with Complex Numbers

When solving quadratic equations using the quadratic formula , you sometimes get a negative value under the square root. In these cases, the equation does not have any real solutions.

But now that you’re working with complex numbers , you’re able to find all the solutions to quadratic equations. The reason for this is the fact that the imaginary unit i can be utilized to find complex solutions to the quadratic formula.

Complex Quadratic Equations

Let a , b , c ∈ ℂ be complex numbers with a ≠ 0 . Then a z 2 + b z + c = 0 has the following solutions:

If the expression b 2 − 4 a c is negative, you have to use the imaginary unit i to find the solutions.

Solve z 2 − 4 z + 5 = 0 for z

You recognize the coefficients of the equation to be a = 1 , b = − 4 and c = 5 . This means that you can use the quadratic formula to find the solutions:

Since you have a negative number inside the square root, the equation has no real solutions. However, by utilizing the imaginary, you can still find complex solutions:

Thus the final solutions to the equation are:

Note! In Example 1 you used the following relation:

This relation does not hold in general for complex numbers. Using this relation for complex numbers can yield inconsistencies. The following is an example of such inconsistencies:

The reason this calculation yields a contradiction is that − 1 ⋅ − 1 ≠ − 1 ⋅ − 1 . The rule stating that a b = a b only holds when both a and b are positive numbers.

By using the quadratic formula, you can even solve quadratic equations involving complex coefficients. In those cases, you need some knowledge about complex roots in order to simplify the expression inside the square root.

Solve 1 2 z 2 + i z + 3 2 i = 0 for z

You recognize the coefficients as a = 1 2 , b = i and c = 3 2 i . This means that you can use the quadratic formula to find the solutions:

All complex numbers w have two square roots. In this case you only need to consider the root whose argument lies in the interval [ 0 , π ) . The reason for this is that both solutions are included in ± w .

In order to find the square root of w = − 1 − 3 i , you first need to write w in polar form . In this case, the norm of w is r = 2 , while the argument is 𝜃 = 4 π 3 . Thus w = 2 e i 4 π 3 in polar form. You can now find the square root of w by taking the square root of the norm of w and dividing the argument of w by 2 . Thus the square root of w is 2 e i 2 π 3 . In Cartesian form, the square root is written as − 2 2 + 6 2 i . Thus the solutions to the equation are:

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.5: Quadratic Equations with Complex Roots

• Last updated
• Save as PDF
• Page ID 40893

• Richard W. Beveridge
• Clatsop Community College

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

In Section \(1.3,\) we considered the solution of quadratic equations that had two real-valued roots. This was due to the fact that in calculating the roots for each equation, the portion of the quadratic formula that is square rooted (\(b^{2}-4 a c,\) often called the discriminant) was always a positive number.

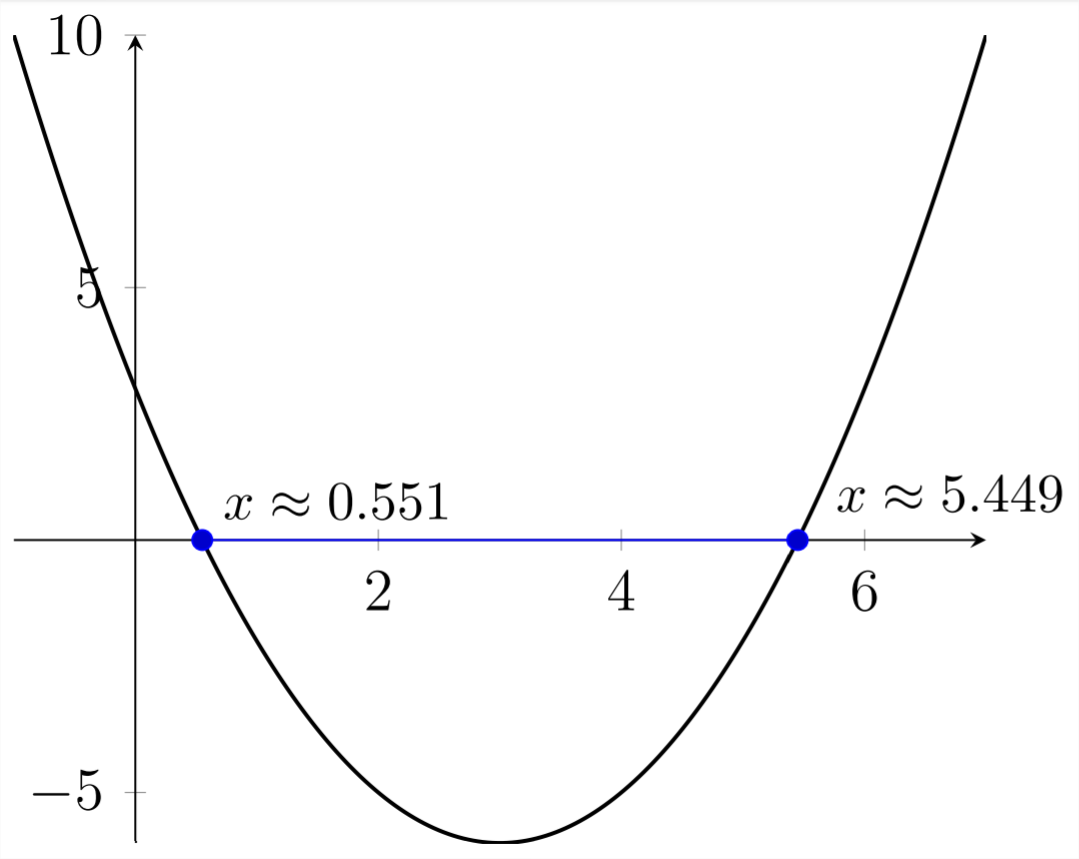
For example, in using the quadratic formula to calculate the the roots of the equation \(x^{2}-6 x+3=0,\) the discriminant is positive and we will end up with two real-valued roots: \[ \begin{array}{c} x^{2}-6 x+3=0 \\ a=1, b=-6, c=3 \\ =\frac{-(-6) \pm \sqrt{(-6)^{2}-4(1)(3)}}{2 * 1} \\ =\frac{6 \pm \sqrt{36-12}}{2} \\ =\frac{6 \pm \sqrt{24}}{2} \\ =\frac{6 \pm 4.899}{2} \end{array} \] \begin{array}{ll} \approx \frac{6+4.899}{2} & \approx \frac{6-4.899}{2} \\ \approx \frac{10.899}{2} & \approx \frac{1.101}{2} \\ \approx 5.449 & \approx 0.551 \end{array}

When we added and subtracted the square root of 24 to 6 in the quadratic formula, this created two answers, and they were real-valued because the square root of 24 is real-valued.

Another way to see this is graphically. If we graph \(y=x^{2}-6 x+3\) and find the \(x\) values that make \(y=0,\) these will appear along the \(x\) -axis, and will be the same values that solve the equation \(x^{2}-6 x+3=0\)

If we consider a related, but slightly different equation to start with, these relationships between the roots, the discriminant and the graphical intersections will be slightly different. \[ \begin{array}{c} x^{2}-6 x+9=0 \\ a=1, b=-6, c=9 \end{array} \]

\begin{aligned} x &=\frac{-(-6) \pm \sqrt{(-6)^{2}-4(1)(9)}}{2 * 1} \\ &=\frac{6 \pm \sqrt{36-36}}{2} \\ &=\frac{6 \pm \sqrt{0}}{2} \\ &=\frac{6}{2}=3 \end{aligned}

Because the discriminant was 0 in this problem, we only get one real-valued answer.

Graphically, the additional 6 that was added to the original equation to change it from \(x^{2}-6 x+3\) to \(x^{2}-6 x+9\) shifts every \(y\) value on the graph up 6 units.

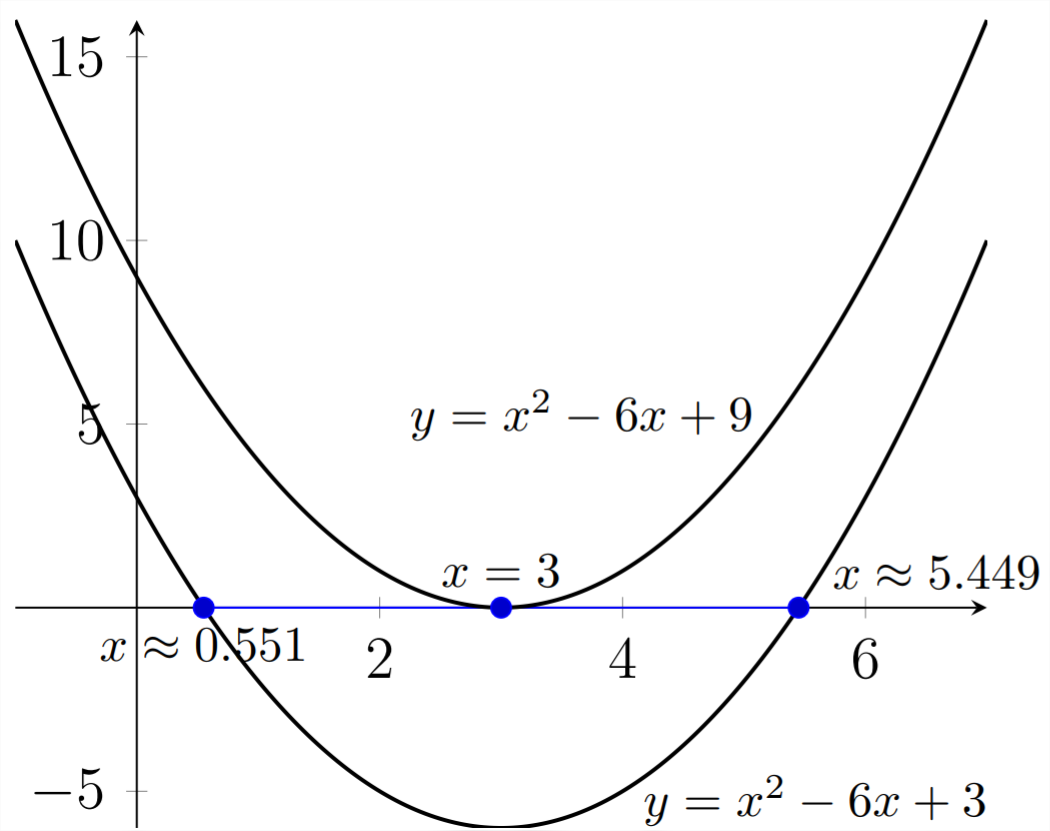
If we add an additional three units to the constant term of this quadratic equation, we encounter a third possibility.

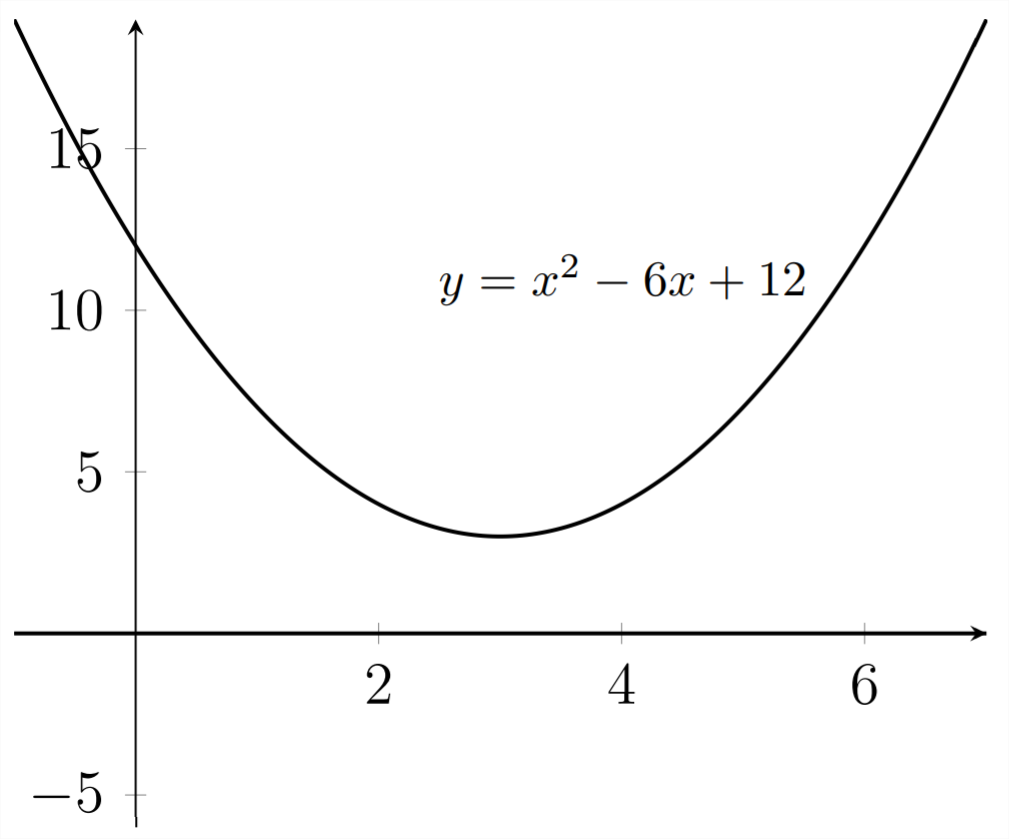
\begin{array}{c} x^{2}-6 x+12=0 \\ a=1, b=-6, c=12 \\ =\frac{-(-6) \pm \sqrt{(-6)^{2}-4(1)(12)}}{2 * 1} \\ =\frac{6 \pm \sqrt{36-48}}{2} \\ =\frac{6 \pm \sqrt{-12}}{2} \\ =\frac{6}{2} \pm \frac{6 \cdot 464 i}{2} \\ \approx 3 \pm 1.732 i \end{array}

Here the discriminant is negative, which leads to two complex-valued answers. If the equation has real-valued coefficients, the complex roots will always come in conjugate pairs. Complex conjugates share the same real-valued part and have opposite signs in their complex-valued (or imaginary) parts: \(a \pm b i\)

Graphically, the previous problem was one step away from not intersecting the \(x\) -axis at all and the additional three units that we added on to get \(y=x^{2}-\) \(6 x+12\) moves the graph entirely away from the \(x\) -axis. Because the roots are complex-valued, we don't see any roots on the \(x\) -axis. The \(x\) -axis contains only real numbers.

since the calculator has been programmed for the quadratic formula, the focus of the problems in this section will be on putting them into standard form.

Example \(\PageIndex{1}\)

Solve for \(x\) \((2 x+1)(x+5)-2 x(x+7)=5(x+3)^{2}\)

\[ \begin{array}{c} (2 x+1)(x+5)-2 x(x+7)=5(x+3)^{2} \\ 2 x^{2}+11 x+5-2 x^{2}-14 x=5(x+3)(x+3) \\ -3 x+5=5\left(x^{2}+6 x+9\right) \\ -3 x+5=5 x^{2}+30 x+45 \\ 0=5 x^{2}+33 x+40 \\ x=5, b=33, c=40 \\ x=-5,-1.6 \end{array} \]

The fact that the roots of this equation were rational numbers means that the equation could have been solved by factoring. \[ \begin{array}{cc} 0=5 x^{2}+33 x+40 \\ 0=(5 x+8)(x+5) \\ 5 x=-8 & x+5=0 \\ 5 x+8=0 & x=-5 \\ x=-1.6 & \end{array} \]

Solve for \(x\) \((x-2)^{2}+3(4 x-1)(x+1) &=7(x+1)(x-1)\)

\[ \begin{aligned} x^{2}-4 x+4+3\left(4 x^{2}+3 x-1\right) &=7\left(x^{2}-1\right) \\ x^{2}-4 x+4+12 x^{2}+9 x-3 &=7 x^{2}-7 \\ 13 x^{2}+5 x+1 &=7 x^{2}-7 \\ 6 x^{2}+5 x+8 &=0 \\ a=6, b=5, c=8 & \\ x \approx-0.41 \overline{6} \pm 1.077 i \approx-\frac{5}{12} \pm 1.077 i \end{aligned} \]

Exercise \(\PageIndex{1}\)

Solve for \(x\) in each equation. Round any irrational values to the nearest 1000 th. 1) \(\quad 3 x^{2}-3 x=4\) 2) \(\quad 4 x^{2}-2 x=7\) 3) \(\quad 5 x^{2}=3-7 x\) 4) \(\quad 3 x^{2}=21-14 x\) 5) \(\quad 6 x^{2}+1=2 x\) 6) \(\quad 5 x-3 x^{2}=17\) 7) \(\quad (5 x-1)(2 x+3)=3 x-20\) 8) \(\quad (x+4)(3 x-1)=9 x-5\) 9) \(\quad (x-2)^{2}=8 x(x-1)+10\) 10) \(\quad (2 x-3)^{2}=2 x-7 x^{2}\) 11) \(\quad (x+5)(x-6)=(2 x-1)(x-4)\) 12) \(\quad (3 x-4)(x+2)=(2 x-5)(x+5)\)

1) \(\quad x \approx 1.758,-0.758\) 3) \(\quad x \approx 0.344,-1.744\) 5) \(\quad x \approx 0.1 \overline{6} \pm 0.373 i\) 7) \(\quad x \approx-0.5 \pm 1.204 i\) 9) \(\quad x \approx 0.286 \pm 0.881 i\) 11) \(\quad x \approx 4 \pm 4.243 i\)

Quadratic Equation Solver

We can help you solve an equation of the form " ax 2 + bx + c = 0 " Just enter the values of a, b and c below :

Is it Quadratic?

Only if it can be put in the form ax 2 + bx + c = 0 , and a is not zero .

The name comes from "quad" meaning square, as the variable is squared (in other words x 2 ).

These are all quadratic equations in disguise:

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• x^4-5x^2+4=0
• \sqrt{x-1}-x=-7
• \left|3x+1\right|=4
• \log _2(x+1)=\log _3(27)
• 3^x=9^{x+5}
• What is the completing square method?
• Completing the square method is a technique for find the solutions of a quadratic equation of the form ax^2 + bx + c = 0. This method involves completing the square of the quadratic expression to the form (x + d)^2 = e, where d and e are constants.
• What is the golden rule for solving equations?
• The golden rule for solving equations is to keep both sides of the equation balanced so that they are always equal.
• How do you simplify equations?
• To simplify equations, combine like terms, remove parethesis, use the order of operations.
• How do you solve linear equations?
• To solve a linear equation, get the variable on one side of the equation by using inverse operations.

equation-calculator

• High School Math Solutions – Quadratic Equations Calculator, Part 1 A quadratic equation is a second degree polynomial having the general form ax^2 + bx + c = 0, where a, b, and c...

Please add a message.

Message received. Thanks for the feedback.