how to solve absolute values equations

Absolute Value in Algebra

Absolute value means ....

... how far a number is from zero:

"6" is 6 away from zero, and "−6" is also 6 away from zero.

So the absolute value of 6 is 6 , and the absolute value of −6 is also 6

Absolute Value Symbol

To show we want the absolute value we put "|" marks either side (called "bars"), like these examples:

More Formal

More formally we have:

Which says the absolute value of x equals:

• x when x is greater than zero
• 0 when x equals 0
• −x when x is less than zero (this "flips" the number back to positive)

So when a number is positive or zero we leave it alone, when it is negative we change it to positive using −x.

Example: what is |−17| ?

Well, it is less than zero, so we need to calculate "−x":

− ( −17 ) = + 17

(Because two minuses make a plus )

Useful Properties

Here are some properties of absolute values that can be useful:

That makes sense ... |a| can never be less than zero.

Squaring a makes it positive or zero (for a as a Real Number). Then taking the square root will "undo" the squaring, but leave it positive or zero.

Means these are the same:

• the absolute value of (a times b), and
• (the absolute value of a) times (the absolute value of b)

Which can also be useful when solving

Which is often the key to solving most absolute value questions.

Example: Solve |x+2| = 5

Using "|u| = a is the same as u = ±a ":

Which has two solutions:

Graphically

Let us graph that example:

It is easier to graph when we have an "=0" equation, so subtract 5 from both sides:

|x+2| − 5 = 0

Now let's plot y=|x+2|−5 and find where it equals zero.

Here is the plot of y=|x+2|−5 , but just for fun let's make the graph by shifting it around :

And the two solutions (circled) are −7 and +3 .

Absolute Value Inequalities

Mixing Absolute Values and Inequalites needs a little care!

There are 4 inequalities:

Less Than, Less Than or Equal To

With " < " and " ≤ " we get one interval centered on zero:

Example: Solve |x| < 3

This means the distance from x to zero must be less than 3:

Everything in between (but not including) −3 and 3

It can be rewritten as:

−3 < x < 3

As an interval it can be written as:

The same thing works for "Less Than or Equal To":

Example: Solve |x| ≤ 3

Everything in between and including -3 and 3

How about a bigger example?

Example: Solve |3x-6| ≤ 12

Rewrite it as:

−12  ≤  3x−6  ≤  12

−6  ≤  3x  ≤  18

Lastly, multiply by (1/3). Because we are multiplying by a positive number, the inequalities will not change:

−2  ≤  x  ≤  6

Greater Than, Greater Than or Equal To

This is different ... we get two separate intervals :

Example: Solve |x| > 3

It looks like this:

less than -3 or from 3 onwards

It can be rewritten as

x < −3   or   x > 3

(−∞, −3) U (3, +∞)

Note: U means "Union" of the two intervals.

Careful! Do not write it as

Because x cannot be less than -3 and greater than 3 at the same time

It is really:

x is less than −3 or greater than 3

The same thing works for "Greater Than or Equal To":

Example: Solve |x| ≥ 3

Can be rewritten as

x ≤ −3   or   x ≥ 3

(−∞, −3] U [3, +∞)

Reset password New user? Sign up

Existing user? Log in

Absolute Value Equations

Already have an account? Log in here.

• Pranshu Gaba
• Alan Enrique Ontiveros Salazar
• Kai Hsien Boo
• Agnishom Chattopadhyay
• Aditya Virani
• Prince Loomba
• Keshav Ramesh

Absolute value equations are equations involving expressions with the absolute value functions . This wiki intends to demonstrate and discuss problem solving techniques that let us solve such equations.

A very basic example would be as follows:

Find all values of \(x\) satisfying \(|x-2| + |x-4| = 4.\)

Usually, the basic approach is to analyze the behavior of the function before and after the point where they reach 0. For example, for \(|x-a|\) one could analyze the cases where \(x > a\) or \(x < a\), or even \(x = a\) if required. However, these problems are often simplified with a more sophisticated approach like being able to eliminate some of the cases, or graphing the functions. In this wiki, we intend to discuss this techniques along with strategies on when to use which.

Methodology

Technique - squaring both sides, technique - casework, technique - sketching graph, problem solving - miscellaneous.

Introduction to absolute value equations

Methodology to solve absolute value equations: the techniques used to solve absolute value equations and when to use which one

Take an example to describe the following methodology:

1) Understanding absolute value--positive, negative case (or graph approach) 2) Determining possible solutions 3) Verifying solutions

Explain - How do we use this technique to solve absolute value equations?

Remember to verify the possible solutions - why and how?

2-3 examples in increasing order of difficulty - explaining how we squared both sides to solve more difficult problems

Followed by 1-2 TIY problems - relevant to be solved by case work technique

Suppose we have an equation of the form \(\lvert a \rvert = \lvert b \rvert\). Since both sides are positive, we can square them without adding extraneous solutions: \[a^2=b^2.\] Then solve it as an ordinary equation: \[\begin{align} a^2-b^2&=0 \\ (a+b)(a-b)&=0. \end{align}\] So we see that \(a=-b\) or \(a=b\).

Solve the equation \(\lvert 3x+4 \rvert = \lvert 2x-7 \rvert\) for real \(x\). We square both sides to obtain \[(3x+4)^2=(2x-7)^2.\] Here we don't need to expand both sides; just apply the difference of two squares to find the factors: \[\begin{align} (3x+4+2x-7)(3x+4-2x+7)&=0 \\ (5x-3)(x+11)&=0. \end{align} \] The solutions are \(\left\{\frac{3}{5}, -11\right\}. \ _ \square\)

Because absolute value can be defined as piecewise functions, depending on where the value of \(x \) is with respect to the number line, you have to work with a different "piece" of the piecewise function.

General steps:

Using the definition of absolute value as a piecewise function, "undo" the absolute value sign(s) and write cases. For example, we know that the expression in the absolute value sign can either be positive or negative.

Solve each case for \( x\).

Verify the solutions.

Find all real values of \(x\) such that \( | 3x – 4 | – 2 = 3.\) We first isolate the absolute value onto one side: \[\begin{align} | 3x – 4 | – 2 & = 3\\ | 3x – 4 | &= 5. \end{align}\] Now, we "undo" the absolute value signs and split the equation into its two cases, the positive case and the negative case: \[\begin{array}{rlcccrl} (3x – 4) &= 5 &&\text{ or } && –(3x – 4) &= 5\\ 3x – 4 &= 5 &&\text{ or } && –3x + 4 &= 5\\ 3x &= 9 &&\text{ or } && –3x &= 1\\ x &= 3 &&\text{ or } && x &= –\frac{1}{3}. \ _\square \end{array}\]

Find all real values of \(x \) such that \( |x+1| + |2x+3| = 5 \). There are four possible cases, but one will be eliminated due to impossibility: Case 1. If \(x+1 \) and \( 2x+3 \) are both positive, then \[\begin{align} x+1 + 2x+3 &= 5 \\ 3x + 4 &= 5 \\ 3x &= 1 \\ x &= \dfrac{1}{3}. \end{align} \] Case 2. If \( x+1 \) is negative and \( 2x + 3 \) is positive, then \[\begin{align} - x - 1 + 2x + 3 &= 5 \\ x + 2 &= 5 \\ x &= 3. \end{align} \] However, when \( x = 3 \), \( x+1 \) and \( 2x+3 \) are both positive, so this is not a valid solution to the equation. Case 3. If \( x+1 \) and \( 2x+3 \) are both negative, then \[\begin{align} -x - 1 - 2x - 3 &= 5 \\ -3x - 4 &= 5 \\ -3x &= 9 \\ x &= -3. \end{align} \] Case 4. If \( x +1 \) is positive and \( 2x + 3 \) is negative, it is an impossible case. Graph the two lines if you are not convinced. Therefore, the solution set is \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\)

Find all real values of \(x\) such that \[|x+2|+|2x+6|+|3x-3|=12.\] In this problem we are dealing with 3 terms of absolute values. Their turning points (the values of \(x\) such that they change sign) of the three terms are \(x=-2, x=-3, x=1,\) respectively. Hence, we need to check the cases \(-\infty < x \leq -3\), \(-3<x\leq -2\), \(-2 < x \leq 1\), \(1<x<\infty\). Case 1. \(\, -\infty < x \leq -3\) In this case, the three terms will always be negative. Hence, \[\begin{aligned} -(x+2)-(2x+6)-(3x-3)&=12 \\ x &= -\frac{17}{6}. \end{aligned}\] However, \(x=-\frac{17}{6} >-3\) is not within the domain \(-\infty < x \leq -3\). Thus this solution is not valid. Case 2. \(\, -3<x\leq -2\) In this case, the three terms will be negative, positive, and negative, respectively. Hence, \[\begin{aligned} -(x+2)+(2x+6)-(3x-3)&=12 \\ x &= -\frac{5}{2}. \end{aligned}\] \(x=-\frac{5}{2}\) lies between \(-3\) and \(-2\). Thus \(\boxed{x=-\frac{5}{2}}\) is one of the solutions. Case 3. \(\, -2 < x \leq 1\) In this case, the three terms will be positive, positive, and negative, respectively. However, \[\begin{aligned} (x+2)+(2x+6)-(3x-3)=11 \neq 12. \end{aligned}\] Thus there is no solution within this domain. Case 4. \(\, 1<x<\infty\) In this case, the three terms are always positive. Hence, \[\begin{aligned} (x+2)+(2x+6)+(3x-3)&=12 \\ x &= \frac{7}{6}, \end{aligned}\] which lies between \(1\) and \(\infty\). Thus \(\boxed{x=\frac{7}{6}}\) is another solution. In conclusion, \(x=-\frac{5}{2}\) and \(x=\frac{7}{6}\) are the solutions for the given equation. \(_\square\)

Find all real values of \( x \) such that \( |x||x+1| = 2 \). Case 1. \(\, x, x+1 \) both positive \[\begin{align} x(x+1)-2 &= 0 \\ x^2 +x - 2 &= 0 \\ x &= 1, x = -2. \end{align} \] Reject \( x = -2 \) because it does not make both \(x \) and \( x +1 \) positive. Case 2. \(\, x\) negative, \( x + 1 \) positive \[\begin{align} -x(x+1)-2 &= 0 \\ -x^2 - x - 2 &= 0 \\ x^2 + x + 2 &= 0 \\ x &= \dfrac{-1 \pm \sqrt{1 - 4 \cdot 1 \cdot 2 }}{2}. \end{align} \] We only asked for real solutions, so at this point we ignore this case because we're going to get imaginary results. Case 3. \(\, x\) positive, \( x +1 \) negative This is an impossible case (graph the lines and you'll see why), so we can ignore it. Case 4. \(\, x, x+1 \) both negative Because they're both negative, the negatives end up "canceling" and become positive, which was what we had in Case 1. However, the restriction is different from Case 1 (here, both \( x \) and \( x +1 \) have to be negative, not positive ), so instead of rejecting \( x = -2 \), we reject \( x = 1 \) from this case. Basically, in this specific case 4, \( x = 1 \) is not a possible solution, but it does not mean it's not a possible solution for Case 1 because we're simply going piece by piece in this piecewise function--in the end we will take the union of all possible solutions. Thus, the solutions are \( \left \{ -2, 1 \right \} \). \(_\square\)

Sometimes absolute value equations have a ridiculous number of cases and it would take too long to go through every single case. Therefore, we can instead graph the absolute value equations using the definition of absolute value as a piecewise function. To get each piece, you must figure out the domain of each piece. This method is highly beneficial when the question writer asks for the number of solutions instead of the actual solutions. Let's work through some examples to see how this is done.

Find all real solutions to \( |3x-4| = 5 \). To graph this, there are two possible cases: when \( 3x - 4\) is positive, and when \( 3x-4 \) is negative. When is \( 3x-4 \) positive? \[\begin{align} 3x - 4 &> 0 \\ 3x &> 4 \\ x &> \dfrac{4}{3}. \end{align} \] (Also, when \( x < \frac{4}{3} \), \( 3x- 4 \) will be negative.) We know that there will be a "turning point" at \( x = \frac{4}{3} \) for the graph of \( y = |3x-4| \). Finally, using the definition of absolute value, we know that when \( x > \frac{4}{3} \), \( y = 3x - 4 \), and when \( x \leqslant \frac{4}{3} \), \( y = -3x + 4 \). We now just need to graph \( y = 5 \) and look for the intersections. You can see that the solutions are \(\left \{ -\frac{1}{3} , 3 \right \}.\ _\square\). Another benefit of this graphing technique is that you do not need to verify any of the solutions--since we are only graphing the pieces that are actually mathematically possible, we get all the solutions we are looking for, no less and no more. If you could not discern the solutions from the picture, you can simply solve the equation for each case.

Find all real solutions to \( |x+1| + |2x+3| = 5 \). The possible cases are that \(\hspace{0.5cm}\) 1. \( \, x+1, 2x+3 \) are both positive; \(\hspace{0.5cm}\) 2. \( \, x+1 \) is negative and \( 2x+3 \) is positive; \(\hspace{0.5cm}\) 3. \( \, x+1 , 2x + 3 \) are both negative. We need to figure out the domains for which each of these holds. Case 1 holds when \( x > -1 \). Case 2 holds when \( -\frac{3}{2} < x< -1 \). Case 3 holds when \( x < -\frac{3}{2} \). Now, let's write our piecewise function. When \( x > -1 \), we have \( y = x+1 + 2x + 3 = 3x + 4 \). When \( -\dfrac{3}{2} < x< -1 \), we have\( y = -x -1 + 2x + 3 = x + 2 \). When \( x < - \dfrac{3}{2} \), we have \( y = -x - 1 -2x - 3 = -3x -4 \). As you can see in the graph, the solutions for the given equation are \(\left \{ -3, \frac{1}{3} \right \}.\ _\square\) .

Find all real solutions to \( |x||x+1| = 2 \). To graph this, we again only look at the possible cases and when they would occur: \(\hspace{0.5cm}\) 1. \(\, x, x+1 \) both positive \(\hspace{0.5cm}\) 2. \(\, x \) negative, \( x+1 \) positive \(\hspace{0.5cm}\) 3. \(\, x, x+1 \) both negative. Case 1 is true when \( x>0 \). Case 2 is true when \( -1 < x < 0 \). Case 3 is true when \( x<-1 \). When \( x>0 \) and when \( x< -1 \), we have \( y = x(x+1) = x^2 + x \). When \( -1 < x < 0 \), we have \( y = -x(x+1) = -x^2 - x \). It is evident that the solutions are \(\{-2, 1\}.\ _\square\)

Any other technique (fact, definition) you can use to solve the problems? Otherwise move on to the followings.

3-4 examples solved by using a mix of more than one of above techniques

Add guiding text in between. Guiding text means phrasing the section in a way that it keeps on telling the reader what's going on in this section.

3-4 TIY problems - using multiple techniques to solve

What is the sum of all real numbers \(x\) satisfying \[ x^2-\sqrt{x^2} = \lvert x-1 \rvert +5?\] Observe that \(\sqrt{x^2}=\lvert x \rvert.\) Then the given equation becomes \[ x^2-\lvert x \rvert= \lvert x-1 \rvert +5.\] If \(x<0,\) then we rewrite the equation to obtain \[\begin{align} x^2-(-x)&=-(x-1)+5\\ x^2+2x-6&=0\\ x&=-1\pm \sqrt{7}\\ x&=-1-\sqrt{7}. \qquad (\text{since } x<0) \end{align}\] If \(0\le x<1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=-(x-1)+5\\ x^2&=6\\ x&=\pm \sqrt{6}, \end{align}\] which do not satisfy the assumption \(0\leq x<1.\) Thus there are no solutions in this interval. If \(x\ge 1,\) then we rewrite the equation to obtain \[\begin{align} x^2-x&=x-1+5\\ x^2-2x-4&=0\\ x&=1\pm \sqrt{5}\\ x&=1+\sqrt{5}. \qquad (\text{since } x\ge 1) \end{align}\] Therefore, the above three cases give two solutions \(x=-1-\sqrt{7}\) and \(x=1+\sqrt{5},\) the sum of which is \(\sqrt{5}-\sqrt{7}.\) \(_\square\)

[IMO 1959/2] Solve the equation \(\sqrt{x+\sqrt{2x-1}}+\sqrt{x-\sqrt{2x-1}}=A\) for real \(x\) (where the square roots are only defined for non-negative values), when \(A=\sqrt{2}\); \(A=1\); \(A=2\). Here we don't see any absolute value involved with the equation. Before doing anything, note that our first restriction for \(x\) is \(x \geq \frac{1}{2}\) and for \(A\) is \(A>0\). Intuitively, we could square both sides to get rid of some square roots: \[\begin{align} x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{x^2-(2x-1)}&=A^2 \\ 2x+2\sqrt{(x-1)^2}&=A^2. \end{align}\] Great! We find a perfect square inside the square root, so an absolute value will appear: \[2x+2|x-1|=A^2.\] Now we are going to find the possible cases for \(A\): When \(x-1 > 0\), we have \[\begin{align} 2x+2(x-1)&=A^2 \\ x&=\dfrac{A^2+2}{4}. \end{align}\] Then, by our assumption of \(x-1 > 0\), we get that this solution only works when \(A^2 > 2\). When \(x-1 \leq 0\), something interesting happens: \[\begin{align} 2x-2(x-1)&=A^2 \\ 2&=A^2. \end{align}\] So, when \(A^2=2 (\text{or }A=\sqrt{2})\), the equation becomes independent of \(x\), implying that any value of the interval \(x \in \left[\frac{1}{2},1\right]\) will be a solution for the first point. When \(A=1\), there are no solutions by our restriction of \(A^2 \geq 2\). Finally, when \(A=2\) we have \[x=\dfrac{2^2+2}{4}=\frac{3}{2}.\ _\square\] What happens if we allow the square roots to admit negative values?

Sometimes, in minimization problems, it often helps us to see that the value of an expression inside the absolute value is at least 0.

No problem found with slug "absolute-warm-up"

Problem Loading...

Note Loading...

Set Loading...

How to solve absolute value equations

|x + 5| = 3.

Worksheet on Abs Val Equations Abs Val Eqn Solver

The General Steps to solve an absolute value equation are:

• Rewrite the absolute value equation as two separate equations, one positive and the other negative
• Solve each equation separately
• After solving, substitute your answers back into original equation to verify that you solutions are valid
• Write out the final solution or graph it as needed

It's always easiest to understand a math concept by looking at some examples so, check outthe many examples and practice problems below.

You can always check your work with our Absolute value equations solver too

Practice Problems

Example equation.

Solve the equation: | X + 5| = 3

Click here to practice more problems like this one , questions that involve variables on 1 side of the equation.

Some absolute value equations have variables both sides of the equation. However, that will not change the steps we're going to follow to solve the problem as the example below shows:

Solve the equation: |3 X | = X − 21

Solve the following absolute value equation: | 5X +20| = 80

Solve the following absolute value equation: | X | + 3 = 2 X

This first set of problems involves absolute values with x on just 1 side of the equation (like problem 2 ).

Solve the following absolute value equation: |3 X −6 | = 21

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

• Mathematicians
• Math Lessons
• Square Roots
• Math Calculators
• Solving Absolute Value Equations – Methods & Examples

JUMP TO TOPIC

What is Absolute Value?

Practice questions, solving absolute value equations – methods & examples.

Solving equations containing an absolute value is as simple as working with regular linear equations . Before we can embark on solving absolute value equations, let’s take a review of what the word absolute value means.

In mathematics, the absolute value of a number refers to the distance of a number from zero, regardless of direction. The absolute value of a number x is generally represented as | x | = a, which implies that, x = + a and -a.

We say that the absolute value of a given number is the positive version of that number . For example, the absolute value of negative 5 is positive 5, and this can be written as: | − 5 | = 5.

Other examples of absolute values of numbers include:  |− 9| = 9, |0| = 0, − |−12| = −12 etc. From these examples of absolute values, we simply define absolute value equations as equations containing expressions with absolute value functions.

How to Solve Absolute Value Equations?

The following are the general steps for solving equations containing absolute value functions:

• Isolate the expression containing the absolute value function.
• Get rid of the absolute value notation by setting up the two equations so that in the first equation, the quantity inside absolute notation is positive. In the second equation, it is negative. You will remove the absolute notation and write the quantity with its suitable sign.
• Calculate the unknown value for the positive version of the equation.
• Solve for the negative version of the equation, in which you will first multiply the value on the other side of the equal sign by -1, and then solve.

In addition to the above steps, there are other important rules you should keep in mind when solving absolute value equations.

• The ∣x∣is always positive: ∣x∣ → +x.
• In | x| = a, if the  a on the right is a positive number or zero, then there is a solution.

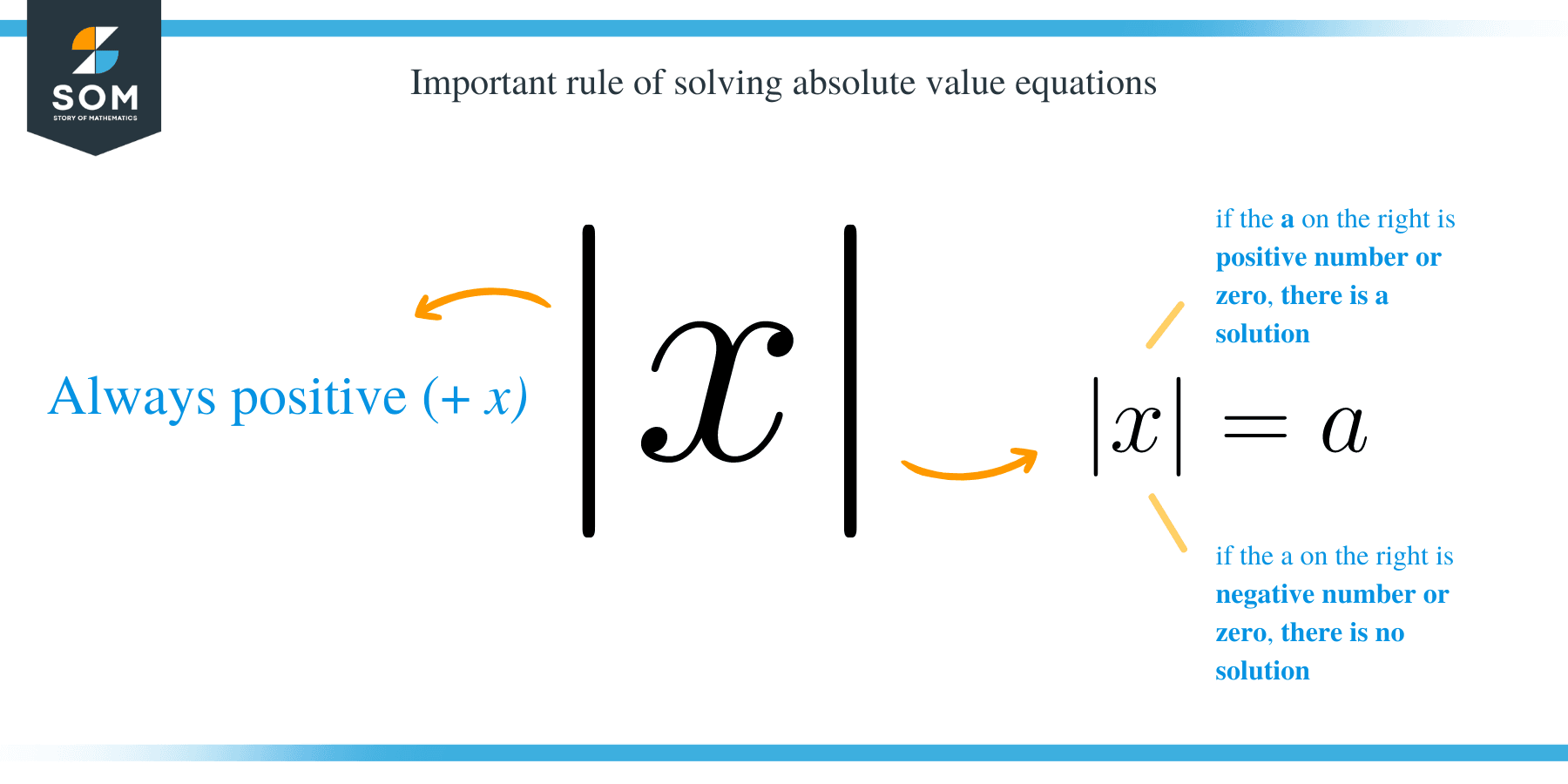
Solve the equation for x: |3 + x| − 5 = 4.

• Isolate the absolute value expression by applying the Law of equations. This means, we add 5 to both sides of the equation to obtain;

| 3 + x | − 5 + 5 = 4 + 5

| 3 + x |= 9

• Calculate for the positive version of the equation. Solve the equation by assuming the absolute value symbols.

| 3 +  x  | = 9 → 3 +  x  = 9

Subtract 3 from both sides of the equation.

3 – 3 + x = 9 -3

• Now calculate for the negative version of the equation by multiplying 9 by -1.

3 +  x  | = 9 → 3 +  x  = 9 × ( −1)

Also subtract 3 from both side to isolate x.

3 -3 + x = – 9 -3

Therefore 6 and -12 are the solutions.

Solve for all real values of x such that | 3x – 4 | – 2 = 3.

• Isolate the equation with absolute function by add 2 to both sides.

= | 3x – 4 | – 2 + 2 = 3 + 2

= | 3x – 4 |= 5

Assume the absolute signs and solve for the positive version of the equation.

| 3x – 4 |= 5→3x – 4 = 5

Add 4 to both sides of the equation.

3x – 4 + 4 = 5 + 4

Divide: 3x/3 =9/3

Now solve for the negative version by multiplying 5 by -1.

3x – 4 = 5→3x – 4 = -1(5)

3x – 4 = -5

3x – 4 + 4 = – 5 + 4

Divide by 3 on both sides.

Therefore, 3 and 1/3 are the solutions.

Solve for all real values of x: Solve | 2 x  – 3 | – 4 = 3

Add 4 to both sides.

| 2 x  – 3 | -4 = 3 →| 2 x  – 3 | = 7

Assume the absolute symbols and solve for the positive version of x.

2 x  – 3 = 7

2x – 3 + 3 = 7 + 3

Now solve for the negative version of x by multiplying 7 by -1

2 x  – 3 = 7→2 x  – 3 = -1(7)

Add 3 to both sides.

2x – 3 + 3 = – 7 + 3

x = – 2

Therefore, x  = –2, 5

Solve for all real numbers of x: | x + 2 | = 7

Already the absolute value expression is isolated, therefore assume the absolute symbols and solve.

| x + 2 | = 7 → x + 2 = 7

Subtract 2 from both sides.

x + 2 – 2 = 7 -2

Multiply 7 by -1 to solve for the negative version of the equation.

x + 2 = -1(7) → x + 2 = -7

Subtract by 2 on both sides.

x + 2 – 2 = – 7 – 2

Therefore, x = -9, 5

Previous Lesson  |  Main Page | Next Lesson

• EXPLORE Random Article

How to Solve Absolute Value Equations

Last Updated: January 31, 2023 References

This article was co-authored by wikiHow Staff . Our trained team of editors and researchers validate articles for accuracy and comprehensiveness. wikiHow's Content Management Team carefully monitors the work from our editorial staff to ensure that each article is backed by trusted research and meets our high quality standards. This article has been viewed 23,120 times.

Setting up the Problem

• For example, |9| = 9; |-9| = -(-9) = 9.

Calculating the Values

Check Your Work

Expert Q&A

• Remember that absolute value bars are distinct from parentheses and function differently. Thanks Helpful 0 Not Helpful 0
• Once you've solved for any variables, remember to simplify absolute values accordingly. Thanks Helpful 0 Not Helpful 0

You Might Also Like

• ↑ http://tutorial.math.lamar.edu/Classes/Alg/SolveAbsValueEqns.aspx
• ↑ https://www.mathsisfun.com/numbers/absolute-value.html
• ↑ http://www.varsitytutors.com/high_school_math-help/solving-absolute-value-equations
• ↑ http://www.purplemath.com/modules/solveabs.htm
• ↑ https://www.khanacademy.org/math/algebra/absolute-value-equations-functions/absolute-value-equations/v/absolute-value-equations

About this article

To solve absolute value equations, first isolate the absolute value terms by moving anything outside of the vertical bars to the other side of the equation. Next, solve for the positive value of the equation by isolating the variable. Since the absolute variable can represent 2 numbers, then solve for the negative value by putting a negative sign outside the vertical bars. Then, move the negative by dividing both sides by -1 and solve for the variable. If you want to learn how to check your answers for an absolute value equation, keep reading the article! Did this summary help you? Yes No

Did this article help you?

• About wikiHow
• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

1.2: Solving Absolute Value Equations

• Last updated
• Save as PDF
• Page ID 134532

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

By the end of this section, you will be able to:

• Solve absolute value equations
• Solve absolute value inequalities with “less than”
• Solve absolute value inequalities with “greater than”
• Solve applications with absolute value

Before you get started, take this readiness quiz.

• Evaluate: \(−|7|\). If you missed this problem, review [link] .
• Fill in \(<,>,<,>,\) or \(=\) for each of the following pairs of numbers. ⓐ \(|−8|\text{___}−|−8|\) ⓑ \(12\text{___}−|−12|\) ⓒ \(|−6|\text{___}−6\) ⓓ \(−(−15)\text{___}−|−15|\) If you missed this problem, review [link] .
• Simplify: \(14−2|8−3(4−1)|\). If you missed this problem, review [link] .

Solve Absolute Value Equations

As we prepare to solve absolute value equations, we review our definition of absolute value .

ABSOLUTE VALUE

The absolute value of a number is its distance from zero on the number line.

The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers.

Absolute values are always greater than or equal to zero.

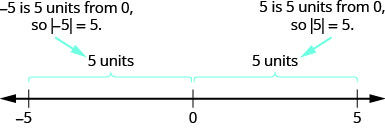
We learned that both a number and its opposite are the same distance from zero on the number line. Since they have the same distance from zero, they have the same absolute value. For example:

• \(−5\) is 5 units away from 0, so \(|−5|=5\).
• \(5\) is 5 units away from 0, so \(|5|=5\).

Figure \(\PageIndex{1}\) illustrates this idea.

For the equation |x|=5,|x|=5, we are looking for all numbers that make this a true statement. We are looking for the numbers whose distance from zero is 5. We just saw that both 5 and −5−5 are five units from zero on the number line. They are the solutions to the equation.

\(\begin{array} {ll} {\text{If}} &{|x|=5} \\ {\text{then}} &{x=−5\text{ or }x=5} \\ \end{array}\)

The solution can be simplified to a single statement by writing \(x=\pm 5\). This is read, “ x is equal to positive or negative 5”.

We can generalize this to the following property for absolute value equations.

ABSOLUTE VALUE EQUATIONS

For any algebraic expression, u , and any positive real number, a ,

\[\begin{array} {ll} {\text{if}} &{|u|=a} \\ {\text{then}} &{u=−a \text{ or }u=a} \\ \nonumber \end{array}\]

Remember that an absolute value cannot be a negative number.

Example \(\PageIndex{1}\)

• \(|y|=−6\)

\(\begin{array} {ll} {} &{|x|=8} \\ {\text{Write the equivalent equations.}} &{x=−8 \text{ or } x=8} \\ {} &{x=\pm 8} \\ \end{array}\)

\(\begin{array} {ll} {} &{|y|=−6} \\ {} &{\text{No solution}} \\ \end{array}\) Since an absolute value is always positive, there are no solutions to this equation.

\(\begin{array} {ll} {} &{|z|=0} \\ {\text{Write the equivalent equations.}} &{z=−0\text{ or }z=0} \\ {\text{Since }−0=0,} &{z=0} \\ \end{array}\) Both equations tell us that z=0z=0 and so there is only one solution.

EXERCISE \(\PageIndex{2}\)

• \(|y|=−4\)

no solution

EXERCISE \(\PageIndex{3}\)

• \(|y|=−5\)

To solve an absolute value equation , we first isolate the absolute value expression using the same procedures we used to solve linear equations. Once we isolate the absolute value expression we rewrite it as the two equivalent equations.

How to Solve Absolute Value Equations

Example \(\pageindex{4}\).

Solve \(|5x−4|−3=8\).

EXERCISE \(\PageIndex{5}\)

Solve: \(|3x−5|−1=6\).

\(x=4, \space x=−\frac{2}{3}\)

EXERCISE \(\PageIndex{6}\)

Solve: \(|4x−3|−5=2\).

\(x=−1,\space x=\frac{5}{2}\)

The steps for solving an absolute value equation are summarized here.

SOLVE ABSOLUTE VALUE EQUATIONS.

• Isolate the absolute value expression.
• Write the equivalent equations.
• Solve each equation.
• Check each solution.

Example \(\PageIndex{7}\)

Solve \(2|x−7|+5=9\).

Exercise \(\PageIndex{8}\)

Solve: \(3|x−4|−4=8\).

\(x=8,\space x=0\)

Exercise \(\PageIndex{9}\)

Solve: \(2|x−5|+3=9\).

\(x=8,\space x=2\)

Remember, an absolute value is always positive!

Example \(\PageIndex{10}\)

Solve: \(|\frac{2}{3}x−4|+11=3\).

\(\begin{array} {ll} {} &{|\frac{2}{3}x−4|=−8} \\ {\text{Isolate the absolute value term.}} &{|\frac{2}{3}x−4|=−8} \\ {\text{An absolute value cannot be negative.}} &{\text{No solution}} \\ \end{array}\)

Exercise \(\PageIndex{11}\)

Solve: \(|\frac{3}{4}x−5|+9=4\).

No solution

Exercise \(\PageIndex{12}\)

Solve: \(|\frac{5}{6}x+3|+8=6\).

Some of our absolute value equations could be of the form \(|u|=|v|\) where u and v are algebraic expressions. For example, \(|x−3|=|2x+1|\).

How would we solve them? If two algebraic expressions are equal in absolute value, then they are either equal to each other or negatives of each other. The property for absolute value equations says that for any algebraic expression, u , and a positive real number, a , if \(|u|=a\), then \(u=−a\) or \(u=a\).

This tell us that

\(\begin{array} {llll} {\text{if}} &{|u|=|v|} &{} &{} \\ {\text{then}} &{|u|=v} &{\text{or}} &{|u|=−v} \\ {\text{and so}} &{u=v \text{ or } u = −v} &{\text{or}} &{u=−v \text{ or } u = −(−v)} \\ \end{array}\)

This leads us to the following property for equations with two absolute values.

EQUATIONS WITH TWO ABSOLUTE VALUES

For any algebraic expressions, u and v ,

\[\begin{array} {ll} {\text{if}} &{|u|=|v|} \\ {\text{then}} &{u=−v\text{ or }u=v} \\ \nonumber \end{array}\]

When we take the opposite of a quantity, we must be careful with the signs and to add parentheses where needed.

Example \(\PageIndex{13}\)

Solve: \(|5x−1|=|2x+3|\).

\(\begin{array} {ll} {} &{} &{|5x−1|=|2x+3|} &{} \\ {} &{} &{} &{} \\ {\text{Write the equivalent equations.}} &{5x−1=−(2x+3)} &{\text{or}} &{5x−1=2x+3} \\ {} &{5x−1=−2x−3} &{\text{or}} &{3x−1=3} \\ {\text{Solve each equation.}} &{7x−1=−3} &{} &{3x=4} \\ {} &{7x=−2} &{} &{x=43} \\ {} &{x=−27} &{\text{or}} &{x=43} \\ {\text{Check.}} &{} &{} &{} \\ {\text{We leave the check to you.}} &{} &{} &{} \\ \end{array}\)

Exercise \(\PageIndex{14}\)

Solve: \(|7x−3|=|3x+7|\).

\(x=−\frac{2}{5}, \space x=\frac{5}{2}\)

Exercise \(\PageIndex{15}\)

Solve: \(|6x−5|=|3x+4|\).

\(x=3, x=19\)

Solve Absolute Value Inequalities with “Less Than”

Let’s look now at what happens when we have an absolute value inequality . Everything we’ve learned about solving inequalities still holds, but we must consider how the absolute value impacts our work. Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line. For the equation \(|x|=5\), we saw that both 5 and \(−5\) are five units from zero on the number line. They are the solutions to the equation.

\[\begin{array} {lll} {} &{|x|=5} &{} \\ {x=−5} &{\text{or}} &{x=5} \\ \nonumber \end{array}\]

What about the inequality \(|x|\leq 5\)? Where are the numbers whose distance is less than or equal to 5? We know \(−5\) and 5 are both five units from zero. All the numbers between \(−5\) and 5 are less than five units from zero (Figure \(\PageIndex{2}\)).

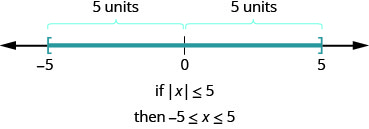
In a more general way, we can see that if \(|u|\leq a\), then \(−a\leq u\leq a\) (Figure \(\PageIndex{3}\)).

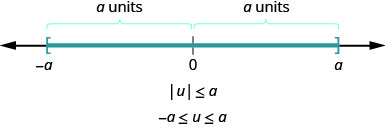
This result is summarized here.

ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)

\[ \text{if} \quad |u|<a, \quad \text{then} \space −a<u<a \\ \text{if} \quad |u|\leq a, \quad \text{then} \space−a\leq u\leq a \nonumber\]

After solving an inequality, it is often helpful to check some points to see if the solution makes sense. The graph of the solution divides the number line into three sections. Choose a value in each section and substitute it in the original inequality to see if it makes the inequality true or not. While this is not a complete check, it often helps verify the solution.

Example \(\PageIndex{16}\)

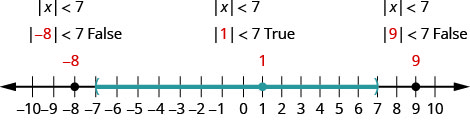
Solve \(|x|<7\). Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −8,−8, 1, and 9.

EXERCISE \(\PageIndex{17}\)

Graph the solution and write the solution in interval notation: \(|x|<9\).

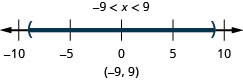
EXERCISE \(\PageIndex{18}\)

Graph the solution and write the solution in interval notation: \(|x|<1\).

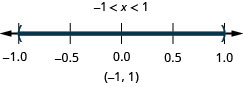
Example \(\PageIndex{19}\)

Solve \(|5x−6|\leq 4\). Graph the solution and write the solution in interval notation.

EXERCISE \(\PageIndex{20}\)

Solve \(|2x−1|\leq 5\). Graph the solution and write the solution in interval notation:

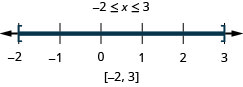
EXERCISE \(\PageIndex{21}\)

Solve \(|4x−5|\leq 3\). Graph the solution and write the solution in interval notation:

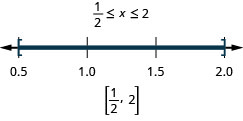
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(<\) OR \(\leq\)

\[\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{−a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{−a\leq u\leq a} \\ \nonumber \end{array}\]

• Solve the compound inequality.
• Graph the solution
• Write the solution using interval notation.

Solve Absolute Value Inequalities with “Greater Than”

What happens for absolute value inequalities that have “greater than”? Again we will look at our definition of absolute value. The absolute value of a number is its distance from zero on the number line.

We started with the inequality \(|x|\leq 5\). We saw that the numbers whose distance is less than or equal to five from zero on the number line were \(−5\) and 5 and all the numbers between \(−5\) and 5 (Figure \(\PageIndex{4}\)).

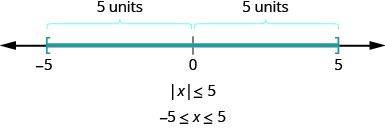
Now we want to look at the inequality \(|x|\geq 5\). Where are the numbers whose distance from zero is greater than or equal to five?

Again both \(−5\) and 5 are five units from zero and so are included in the solution. Numbers whose distance from zero is greater than five units would be less than \(−5\) and greater than 5 on the number line (Figure \(\PageIndex{5}\)).

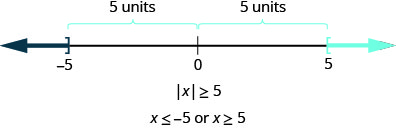
In a more general way, we can see that if \(|u|\geq a\), then \(u\leq −a\) or \(u\leq a\). See Figure .

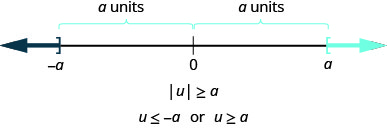
ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\)

\[\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\quad \text{then } u<−a \text{ or } u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\quad \text{then } u\leq −a \text{ or } u\geq a} \\ \nonumber \end{array}\]

Example \(\PageIndex{22}\)

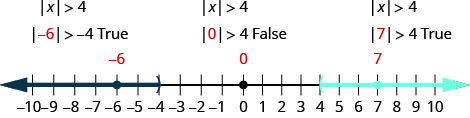
Solve \(|x|>4\). Graph the solution and write the solution in interval notation.

To verify, check a value in each section of the number line showing the solution. Choose numbers such as −6,−6, 0, and 7.

EXERCISE \(\PageIndex{23}\)

Solve \(|x|>2\). Graph the solution and write the solution in interval notation.

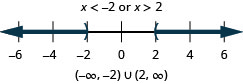
EXERCISE \(\PageIndex{24}\)

Solve \(|x|>1\). Graph the solution and write the solution in interval notation.

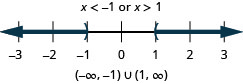
Example \(\PageIndex{25}\)

Solve \(|2x−3|\geq 5\). Graph the solution and write the solution in interval notation.

EXERCISE \(\PageIndex{26}\)

Solve \(|4x−3|\geq 5\). Graph the solution and write the solution in interval notation.

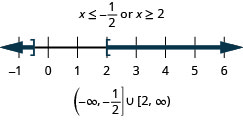
EXERCISE \(\PageIndex{27}\)

Solve \(|3x−4|\geq 2\). Graph the solution and write the solution in interval notation.

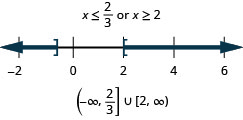
SOLVE ABSOLUTE VALUE INEQUALITIES WITH \(>\) OR \(\geq\).

\[\begin{array} {lll} { |u| >a } &{\quad \text{is equivalent to}} &{ u<−a \quad \text{ or } \quad u>a} \\ { |u| \geq a } &{\quad \text{is equivalent to}} &{ u\leq −a \quad \text{ or } \quad u\geq a} \\ { |u| >a } &{\quad \text{is equivalent to}} &{ u<−a \quad \text{ or } \quad u>a} \\ { |u| \geq a } &{\quad \text{is equivalent to}} &{ u\leq −a \quad \text{ or } \quad u\geq a} \\ \nonumber \end{array}\]

Solve Applications with Absolute Value

Absolute value inequalities are often used in the manufacturing process. An item must be made with near perfect specifications. Usually there is a certain tolerance of the difference from the specifications that is allowed. If the difference from the specifications exceeds the tolerance, the item is rejected.

\[|\text{actual-ideal}|\leq \text{tolerance} \nonumber\]

Example \(\PageIndex{28}\)

The ideal diameter of a rod needed for a machine is 60 mm. The actual diameter can vary from the ideal diameter by \(0.075\) mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

\(\begin{array} {ll} {} &{\text{Let }x=\text{ the actual measurement}} \\ {\text{Use an absolute value inequality to express this situation.}} &{|\text{actual-ideal}|\leq \text{tolerance}} \\ {} &{|x−60|\leq 0.075} \\ {\text{Rewrite as a compound inequality.}} &{−0.075\leq x−60\leq 0.075} \\ {\text{Solve the inequality.}} &{59.925\leq x\leq 60.075} \\ {\text{Answer the question.}} &{\text{The diameter of the rod can be between}} \\ {} &{59.925 mm \text{ and } 60.075 mm.} \\ \end{array}\)

ExERCISE \(\PageIndex{29}\)

The ideal diameter of a rod needed for a machine is 80 mm. The actual diameter can vary from the ideal diameter by 0.009 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

The diameter of the rod can be between 79.991 and 80.009 mm.

ExERCISE \(\PageIndex{30}\)

The ideal diameter of a rod needed for a machine is 75 mm. The actual diameter can vary from the ideal diameter by 0.05 mm. What range of diameters will be acceptable to the customer without causing the rod to be rejected?

The diameter of the rod can be between 74.95 and 75.05 mm.

Access this online resource for additional instruction and practice with solving linear absolute value equations and inequalities.

• Solving Linear Absolute Value Equations and Inequalities

Key Concepts

• Absolute Value The absolute value of a number is its distance from 0 on the number line. The absolute value of a number n is written as \(|n|\) and \(|n|\geq 0\) for all numbers. Absolute values are always greater than or equal to zero.
• Absolute Value Equations For any algebraic expression, u , and any positive real number, a , \(\begin{array} {ll} {\text{if}} &{\quad |u|=a} \\ {\text{then}} &{\quad u=−a \text{ or } u=a} \\ \end{array}\) Remember that an absolute value cannot be a negative number.
• Equations with Two Absolute Values For any algebraic expressions, u and v , \(\begin{array} {ll} {\text{if}} &{\quad |u|=|v|} \\ {\text{then}} &{\quad u=−v \text{ or } u=v} \\ \end{array}\)
• Absolute Value Inequalities with \(<\) or \(\leq\) For any algebraic expression, u , and any positive real number, a , \(\begin{array} {llll} {\text{if}} &{\quad |u|=a} &{\quad \text{then}} &{−a<u<a} \\ {\text{if}} &{\quad |u|\leq a} &{\quad \text{then}} &{−a\leq u\leq a} \\ \end{array}\)
• Write the equivalent compound inequality. \(\begin{array} {lll} {|u|<a} &{\quad \text{is equivalent to}} &{\quad −a<u<a} \\ {|u|\leq a} &{\quad \text{is equivalent to}} &{\quad −a\leq u\leq a} \\ \end{array}\)
• Write the solution using interval notation
• Absolute Value Inequalities with \(>\) or \(\geq\) For any algebraic expression, u , and any positive real number, a , \(\begin{array} {lll} {\text{if}} &{\quad |u|>a,} &{\text{then } u<−a\text{ or }u>a} \\ {\text{if}} &{\quad |u|\geq a,} &{\text{then } u\leq −a\text{ or }u\geq a} \\ \end{array}\)
• Write the equivalent compound inequality. \(\begin{array} {lll} {|u|>a} &{\quad \text{is equivalent to}} &{\quad u<−a\text{ or }u>a} \\ {|u|\geq a} &{\quad \text{is equivalent to}} &{\quad u\leq −a\text{ or }u\geq a} \\ \end{array}\)

• HW Guidelines
• Study Skills Quiz
• Find Local Tutors
• Demo MathHelp.com
• Join MathHelp.com

Select a Course Below

• ACCUPLACER Math
• Math Placement Test
• PRAXIS Math
• + more tests
• 5th Grade Math
• 6th Grade Math
• Pre-Algebra
• College Pre-Algebra
• Introductory Algebra
• Intermediate Algebra
• College Algebra

Solving Simpler Absolute-Value Equations

Simpler Harder Special Case

When we take the absolute value of a number, we always end up with a positive number (or zero). Whether the input was positive or negative (or zero), the output is always positive (or zero). For instance, | 3 | = 3 , and | −3 | = 3 also.

This property — that both the positive and the negative become positive — makes solving absolute-value equations a little tricky. But once you learn the "trick", they're not so bad. Let's start with something simple:

Content Continues Below

MathHelp.com

Solving Absolute Value Equations

Solve | x | = 3

I've pretty much already solved this, in my discussion above:

| −3 | = 3

So then x must be equal to 3 or equal to −3 .

But how am I supposed to solve this if I don't already know the answer? I will use the positive / negative property of the absolute value to split the equation into two cases, and I will use the fact that the "minus" sign in the negative case indicates "the opposite sign", not "a negative number".

For example, if I have x = −6 , then " − x " indicates "the opposite of x " or, in this case, −(−6) = +6 , a positive number. The "minus" sign in " − x " just indicates that I am changing the sign on x . It does not indicate a negative number. This distinction is crucial!

Whatever the value of x might be, taking the absolute value of x makes it positive. Since x might originally have been positive and might originally have been negative, I must acknowledge this fact when I remove the absolute-value bars. I do this by splitting the equation into two cases. For this exercise, these cases are as follows:

a. If the value of x was non-negative (that is, if it was positive or zero) to start with, then I can bring that value out of the absolute-value bars without changing its sign, giving me the equation x = 3 .

b. If the value of x was negative to start with, then I can bring that value out of the absolute-value bars by changing the sign on x , giving me the equation − x = 3 , which solves as x = −3 .

Then my solution is

x = ±3

We can, by the way, verify the above solution graphically. When we attempt to solve the absolute-value equation | x  | = 3 , we are, in effect, setting two line equations equal to each other and finding where they cross. For instance:

In the above, I've plotted the graph of y 1  = |  x  | (being the blue line that looks like a "V") and y 2  = 3 (being the green horizontal line). These two graphs cross at x  = −3 and at x  = +3 (being the two red dots).

If you're wanting to check your answers on a test (before you hand it in), it can be helpful to plug each side of the original absolute-value equation into your calculator as their own functions; then ask the calculator for the intersection points.

Of course, any solution can also be verified by plugging it back into the original exercise, and confirming that the left-hand side (LHS) of the equation simplifies to the same value as does the right-hand side (RHS) of the equation. For the equation above, here's my check:

x = −3

LHS: | x | = | −3 |

LHS: | x | = | +3 |

If you're ever in doubt about your solution to an equation, try graphing or else try plugging your solution back into the original question. Checking your work is always okay!

The step in the above, where the absolute-value equation was restated in two forms, one with a "plus" and one with a "minus", gives us a handy way to simplify things: When we have isolated the absolute value and go to take off the bars, we can split the equation into two cases; we will signify these cases by placing a "minus" on the opposite side of the equation (for one case) and a "plus" on the opposite side (for the other). Here's how this works:

Solve | x + 2 | = 7 , and check your solution(s).

Advertisement

The absolute value is isolated on the left-hand side of the equation, so it's already set up for me to split the equation into two cases. To clear the absolute-value bars, I must split the equation into its two possible two cases, one each for if the contents of the absolute-value bars (that is, if the "argument" of the absolute value) is negative and if it's non-negative (that is, if it's positive or zero). To do this, I create two new equations, where the only difference between then is the sign on the right-hand side. First, I'll do the "minus" case:

x + 2 = −7

x = −9

Now I'll do the non-negative case, where I can just drop the bars and solve:

Now I need to check my solutions. I'll do this by plugging them back into the original equation, since the grader can't see me checking plots on my graphing calculator.

x = −9:

LHS: |(−9) + 2|

= |−7| = 7 = RHS

LHS: |(5) + 2|

= |7| = 7 = RHS

Both solutions check, so my answer is:

x = −9, 5

Solve | 2 x − 3 | − 4 = 3

First, I'll isolate the absolute-value part of the equation; that is, I'll get the absolute-value expression by itself on one side of the "equals" sign, with everything else on the other side:

| 2 x − 3 | − 4 = 3

| 2 x − 3 | = 7

Now I'll clear the absolute-value bars by splitting the equation into its two cases, one for each sign on the argument. First I'll do the negative case:

2 x − 3 = −7

2 x = −4

x = −2

And then I'll do the non-negative case:

2 x − 3 = 7

The exercise doesn't tell me to check, so I won't. (But, if I'd wanted to, I could have plugged "abs(2X−3)−4" and "3" into my calculator (as Y1 and Y2, respectively), and seen that the intersection points were at my x -values.) My answer is:

x = −2, 5

URL: https://www.purplemath.com/modules/solveabs.htm

Page 1 Page 2 Page 3

Standardized Test Prep

College math, homeschool math, share this page.

• Terms of Use
• About Purplemath
• About the Author
• Tutoring from PM
• Advertising
• Linking to PM
• Site licencing

Solver Title

Generating PDF...

• Pre Algebra Order of Operations Factors & Primes Fractions Long Arithmetic Decimals Exponents & Radicals Ratios & Proportions Percent Modulo Number Line Expanded Form Mean, Median & Mode
• Algebra Equations Inequalities System of Equations System of Inequalities Basic Operations Algebraic Properties Partial Fractions Polynomials Rational Expressions Sequences Power Sums Interval Notation Pi (Product) Notation Induction Logical Sets Word Problems
• Pre Calculus Equations Inequalities Scientific Calculator Scientific Notation Arithmetics Complex Numbers Polar/Cartesian Simultaneous Equations System of Inequalities Polynomials Rationales Functions Arithmetic & Comp. Coordinate Geometry Plane Geometry Solid Geometry Conic Sections Trigonometry
• Calculus Derivatives Derivative Applications Limits Integrals Integral Applications Integral Approximation Series ODE Multivariable Calculus Laplace Transform Taylor/Maclaurin Series Fourier Series Fourier Transform
• Functions Line Equations Functions Arithmetic & Comp. Conic Sections Transformation
• Linear Algebra Matrices Vectors
• Trigonometry Identities Proving Identities Trig Equations Trig Inequalities Evaluate Functions Simplify
• Statistics Mean Geometric Mean Quadratic Mean Average Median Mode Order Minimum Maximum Probability Mid-Range Range Standard Deviation Variance Lower Quartile Upper Quartile Interquartile Range Midhinge Standard Normal Distribution
• Physics Mechanics
• Chemistry Chemical Reactions Chemical Properties
• Finance Simple Interest Compound Interest Present Value Future Value
• Economics Point of Diminishing Return
• Conversions Roman Numerals Radical to Exponent Exponent to Radical To Fraction To Decimal To Mixed Number To Improper Fraction Radians to Degrees Degrees to Radians Hexadecimal Scientific Notation Distance Weight Time Volume
• Pre Algebra
• One-Step Addition
• One-Step Subtraction
• One-Step Multiplication
• One-Step Division
• One-Step Decimals
• Two-Step Integers
• Two-Step Add/Subtract
• Two-Step Multiply/Divide
• Two-Step Fractions
• Two-Step Decimals
• Multi-Step Integers
• Multi-Step with Parentheses
• Multi-Step Rational
• Multi-Step Fractions
• Multi-Step Decimals
• Solve by Factoring
• Completing the Square
• Quadratic Formula
• Biquadratic
• Logarithmic
• Exponential
• Rational Roots
• Floor/Ceiling
• Equation Given Roots
• Newton Raphson
• Substitution
• Elimination
• Cramer's Rule
• Gaussian Elimination
• System of Inequalities
• Perfect Squares
• Difference of Squares
• Difference of Cubes
• Sum of Cubes
• Polynomials
• Distributive Property
• FOIL method
• Perfect Cubes
• Binomial Expansion
• Negative Rule
• Product Rule
• Quotient Rule
• Expand Power Rule
• Fraction Exponent
• Exponent Rules
• Exponential Form
• Logarithmic Form
• Absolute Value
• Rational Number
• Powers of i
• Complex Form
• Partial Fractions
• Is Polynomial
• Leading Coefficient
• Leading Term
• Standard Form
• Complete the Square
• Synthetic Division
• Linear Factors
• Rationalize Denominator
• Rationalize Numerator
• Identify Type
• Convergence
• Interval Notation
• Pi (Product) Notation
• Boolean Algebra
• Truth Table
• Mutual Exclusive
• Cardinality
• Caretesian Product
• Age Problems
• Distance Problems
• Cost Problems
• Investment Problems
• Number Problems
• Percent Problems
• Addition/Subtraction
• Multiplication/Division
• Dice Problems
• Coin Problems
• Card Problems
• Pre Calculus
• Linear Algebra
• Trigonometry
• Conversions

Most Used Actions

Number line.

• \left|3x+1\right|=4
• \left|a-6\right|=\left|6-a\right|
• 1.5\left|3p\right|=4.5
• 4\left|2x-8\right|=9
• \left|3x+4\right|=-3
• 5-\left|2(x+3)\right|=0

absolute-equation-calculator

• High School Math Solutions – Absolute Value Equation Calculator Solving absolute value equations is somewhat tricky; it requires understanding of the absolute value property....

Please add a message.

Message received. Thanks for the feedback.

Absolute Value Equation Calculator

What do you want to calculate.

• Solve for Variable
• Practice Mode
• Step-By-Step

Example (Click to try)

About absolute value equations.

• Get the absolve value expression by itself.
• Set up two equations and solve them separately.

Absolute Value Equation Video Lesson

• Khan Academy Video: Absolute Value Equations

Need more problem types? Try MathPapa Algebra Calculator

Clear Absolute Value Equation Calculator »

• School Guide
• Mathematics
• Number System and Arithmetic
• Trigonometry
• Probability
• Mensuration
• Maths Formulas
• Class 8 Maths Notes
• Class 9 Maths Notes
• Class 10 Maths Notes
• Class 11 Maths Notes
• Class 12 Maths Notes
• Solving Absolute Value Equations
• Absolute Value
• Linear Inequalities
• Real-Life Applications of Absolute Value
• Compound Inequalities
• Inequalities
• Mean Absolute Deviation
• Absolute Value of a Complex Number
• Quadratic Inequalities
• Inequalities in LaTeX
• Ruby | BigDecimal absolute value
• Get the absolute values in Pandas
• Ruby | BigDecimal class absolute value
• Python | Absolute value of list elements
• Python - Absolute Tuple Summation
• GRE Algebra | Solving Linear Inequalities
• Program to find absolute value of a given number
• Getting square of absolute value in Julia - abs2() Method
• Minimize the maximum value of the absolute difference

Absolute Value Inequalities

Inequalities that involve algebraic expressions with absolute value symbols and inequality symbols are called Absolute Value Inequality. In this article, we will discuss inequalities and absolute value inequalities and others in detail.

Table of Content

What is Inequalities?

What is absolute value inequalities, solving absolute value inequalities, types of absolute value inequalities, intersection and union in absolute value inequalities, examples on absolute value inequalities.

Inequalities can be understood as the complement of equations. Inequalities are used to establish a relationship between two or more mathematical values based on the unequal relationship between them. Let us look at an example

• 5 + x > y + 10
• x > y + 5

The above relationship indicates that x is not equal to y+5 rather it is greater than the value of y after 5 is added to it.

Absolute Value Inequalities are a subcategory of inequalities that compare absolute values of mathematical quantities. These usually include symbols like >, < which denote unequal relationships.

What is Absolute Value?

Let us see the formal definition

An absolute value inequality is an expression that uses absolute value expression and variables to denote the relationship between quantities.

We can categorize the inequality into two major types:

• Lesser Than or Equal To
• Greater Than or Equal To
• Compound Inequalities with Absolute Values

Each of the given types is denoted using different symbols which will be discussed later.

Example of Absolute Value Inequalities

Here are some examples to understand the Absolute Value Inequalities

• |x + 5| < 8
• -13 < x < 3

We use number line approach to solve an inequality and follow the steps added below:

Step 1: Write down the inequality and assume it to be an equality making it an equation instead of inequation. Step 2: Draw a number line depending on the intervals and represent the equation on the number line. Step 3: From each interval, select a number and check if it satisfies the inequality. Step 4: Perform step 3 for every interval and the intervals for which a random number satisfies the inequality will be included in your final answer. Step 5: Take the union of all the intervals to get the answer.

Graphical Representation of Inequalities

We can use a graph to plot the inequalities and find the corresponding solution for the inequalities. Let us see how we can use the graph to plot the solution

Note: Open dot ◌ is used for representing an open interval whereas a closed dot ⚈ is used to represent a closed interval in the graph.

Here is the representation of different cases:

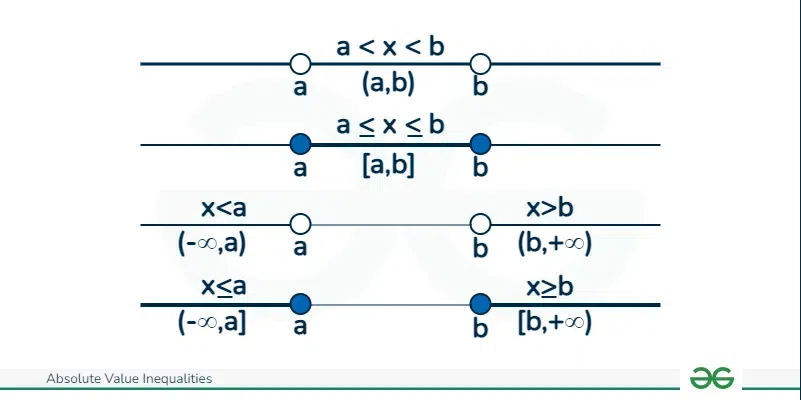
Representation of Inequalities

Depending on the type of sign in the inequality, there are different types of inequalities which are mentioned below:

Inequalities with Greater Than Condition

Inequalities with less than condition, compound inequalities involving absolute values.

These inequalities generally use a greater than sign i.e. the number is greater than the value of some other mathematical value. Here are some examples of such inequalities

• x+ y > 7 + 3y
• 65y > x + 22

These inequalities generally use a less-than sign i.e. the number is less than the value of some other mathematical value. Here are some examples of such inequalities

• x + y < 89
• 5y + 6x < 0

As the name suggests, Compound Inequalities involve both greater than and less than cases i.e. the number is less than and greater than the value of some other mathematical value. These inequalities use the absolute value. Here are some examples of such inequalities

• |x – 5| < 7
• |x + 6y| > 89
• |4x + 2| <= 24

Let us understand how we can take Intersection and Union in Absolute Value Inequalities.

Union of Inequalities

For a given set of values, if the inequality is x>=a or x<b then we need to find the union of the values of x which can be given by

Case 1: x >= a or x < b

{x: x < b U x ≥ a}

Case 2: x < a or x >= b

{x: x <a U x ≥ b} = {x: x < a}∪{x: x ≥ b}.

The solution i.e. the union can be calculated using graph. Consider the example x <= 3 || x >= -4 , then the union of the inequalities will give an overlapping interval which will include all real numbers as shown below.

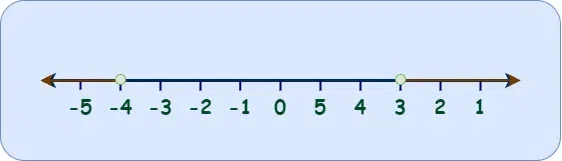
Intersection of Inequalities

For a given set of values, if the inequality is x >= a and x < b then we need to find the intersection of the values of x which can be given by

Case 1: a <= x < b

{x: a≤x < b}

Case 2: a <= x U b > x

{x: a ≤ x U x < b}

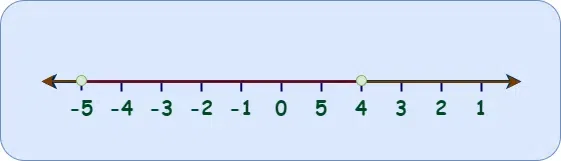
The solution i.e. the intersection can be calculated using graph. Consider the example x <= 4 U x >= -5 , then the intersection of the inequalities will give an interval which will include all real numbers from -5 and 4 as shown below.

Triangle Inequality Compound Inequalities Word Problems of Linear Inequalities

Example 1: Solve for inequality |x+24|>-5 using the formula-based approach.

Given Inequality |x + a| > b -∞ < x + a < -b b < x + a < +∞ Solving both of them individually Case 1: -∞ < x < -a – b Case 2: b – a < x < ∞ x ⋿ (-∞,-a-b) ⋃ (b-a, ∞)

Example 2: Solve this less than equal to absolute inequality |y + 5| <= 3y

Given Inequality |y + 5| <= 3y Case 1: y + 5 <= 3y 5 <= 2y 5/2 <= y y ϵ [5/2, ∞)…(i) Case 2: -3y <= y + 5 -4y <= 5 y >= -1.25 y ϵ (-∞, -5/4]…(ii) From eq. (i) and eq. (ii) y ϵ [5/2, -5/4]

Practice Problems on Absolute Value Inequalities

P1. Use the union and intersection method to find the solution for x given |x+7|<1001 and |x+2|>24.

P2. Use the graphical representation method to find the solution of |2x+5|+y>7x

P3. Solve the inequality ∣2x + 3∣ < 5.

P4. Find all values of such that ∣x − 4∣ ≥ 2.

FAQs Absolute Value Inequalities

When do we use curved and square brackets while writing the solution of inequality.

Curved bracket i.e. ( ) is used to denote a quantity that is not included in the range of possible values of the variable whereas the square bracket i.e. [ ] is used when the number is included in the range of values of the variable.

What are the equivalents of curved and square brackets in graphical representation?

Open dot denotes the curved bracket. Closed dot is used instead of the square bracket.

When is the sign switched from negative to positive and vice-versa in an inequality?

Sign in an inequality changes when we multiply the quantity on both sides of the equation by a negative sign or divide the quantity on both sides by a negative value.

Can an absolute value inequality be negative?

No, absolute value inequality can never be negative.

Please Login to comment...

Similar reads.

• linear algebra
• School Learning

Improve your Coding Skills with Practice

What kind of Experience do you want to share?