

Factoring Algebraic Expressions Word Problems
Factorization of algebraic means finding the factors of the given expression which refers to finding two or more expressions whose product is the given expression. This process of finding two or more expressions whose product is the given expression is known as the factorization of algebraic expressions. A factor is a number that divides the given number without any remainder. It simply means expressing a number as a multiplication of two other numbers. Similarly, in Algebra we write the algebraic expressions as a product of their factors. The only difference here is that an algebraic expression involves numbers and variables combined with an arithmetic operation like addition or subtraction.
1. Read the word problem and determine the greatest common factor of the terms. 2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. 3. Verify your answer by multiplying the factors to get the original expression.
A rectangular garden is being separated into 6 equal sections for different types of flowers. The area of the garden is (12x + 30) square meters. What is the area of each section of the garden?
1. Find the greatest common factor of the two terms. The greatest common factor of 12 and 30 is 6.
2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. (12x + 30) = (6 ● 2x) + (6 ● 5) 6(2x + 5)
3. Verify your answer by multiplying the factors to get the original expression. 6(2x + 5) 12x + 30
Therefore, the area of each section of the garden is (2x + 5) square meters.
Practice Factoring Algebraic Expressions Word Problems
Practice Problem 1
Practice Problem 2
Practice Problem 3
Factor – is a number that divides the given number without any remainder.
Linear Expression – an algebraic expression in which the variable is raised to the first power, and variables are not multiplied or divided.
Term – either a single number or variable, or numbers and variables multiplied together. Terms are separated by + or − signs.
Like terms – Terms that have the same power for the same variables. In like terms, one can only change the numerical coefficient.
Unlike terms – Terms that have different variables or the same variables raised to different powers.
Distributive Property – to multiply a sum or difference by a number, multiply each term inside the parenthesis by the number outside the parenthesis.
Constant – a term without a variable.
Variable – In algebra, a symbol (usually a letter) standing in for an unknown numerical value in an equation or expression.
Coefficient – is an integer that is multiplied with the variable of a single term or the terms of a polynomial.
Pre-requisite Skills Identify Factors Greatest Common Factor-GCF Arithmetic Sequences Geometric Sequences The Distributive Property Simplifying Complex Algebraic Expressions Add Linear Expressions Subtract Linear Expressions
Related Skills Solve One-Step Equations by Addition and Subtraction Solve One-Step Equations by Multiplying and Dividing Solve Equations with Rational Coefficients Solve Two-Step Equations Solve Complex Equations Solve Equations with Rational Coefficients Solve Two-Step Equations Write Two-Step Equations Solve Two-Sided Equations with Rational Coefficients Solve Multi-Step Equations
Calcworkshop
How to Solve Factoring Problems? 9 Amazing Examples!
// Last Updated: January 20, 2020 - Watch Video //
Polynomials and factoring impact our day-to-to lives.

Jenn, Founder Calcworkshop ® , 15+ Years Experience (Licensed & Certified Teacher)
Don’t believe me?
The next time you go outside look up at a building and notice its structure. Or take a walk along a sidewalk or patio and observe how the stones lie upon the ground. Admire a picture frame, and see the sharp, precise corners. Look up in the sky and watch the birds fly overhead.
All of these real-world encounters can be can be defined mathematically using polynomial factoring! And we’re going to learn how to solve these types of factoring applications .
And these factoring applications help us to explain the world around us, as ck-12 nicely states. We can measure the time it takes for a ball to hit the ground after being thrown. We can calculate the size of the perfect rug that will lay in our living room. Or better understand how to play our most favorite video games.
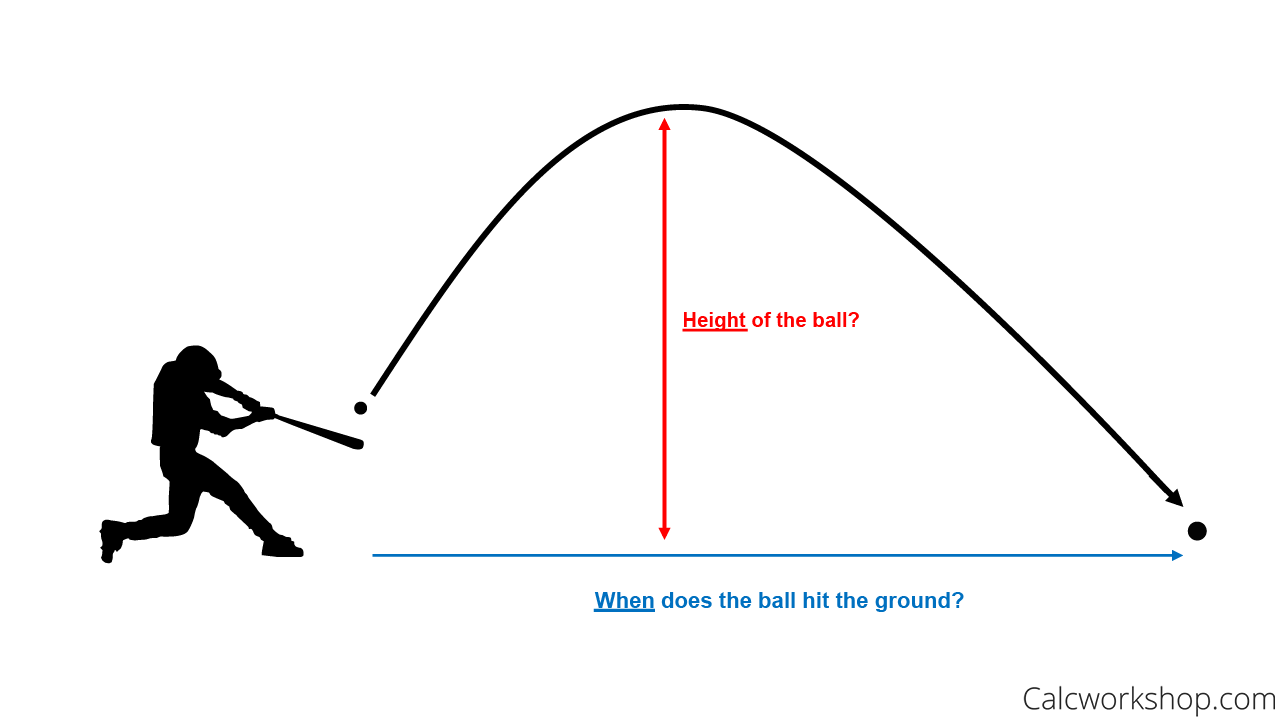
Finding Distances and Time Traveled using Polynomials
So, together we are going to look at factoring in the real world, and see how to solve word problems involving area and perimeter, height, speed, and distance.
But it is important to note that while these problems lead to polynomial equations that can be solved by factoring, not all solutions will satisfy the given conditions.
What this means, is that we may have to discard solutions that don’t make sense.
For example, we know that a negative number cannot represent the length of a rectangle or the distance a car travels, so we will need to make sure that we always check our solutions to ensure their reasonableness.
Factoring Word Problems (How-To) – Video
Get access to all the courses and over 450 HD videos with your subscription
Monthly and Yearly Plans Available
Get My Subscription Now
Still wondering if CalcWorkshop is right for you? Take a Tour and find out how a membership can take the struggle out of learning math.


Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.
Chapter 7: Factoring
7.6 Factoring Quadratics of Increasing Difficulty
Factoring equations that are more difficult involves factoring equations and then checking the answers to see if they can be factored again.
Example 7.6.1
Factor [latex]y^4 - 81x^4[/latex].
This is a standard difference of squares that can be rewritten as [latex](y^2)^2 - (9x^2)^2[/latex], which factors to [latex](y^2 - 9x^2)(y^2 + 9x^2)[/latex]. This is not completely factored yet, since [latex](y^2 - 9x^2)[/latex] can be factored once more to give [latex](y - 3x)(y + 3x)[/latex].
Therefore, [latex]y^4 - 81x^4 = (y^2 + 9x^2)(y - 3x)(y + 3x)[/latex].
This multiple factoring of an equation is also common in mixing differences of squares with differences of cubes.
Example 7.6.2
Factor [latex]x^6 - 64y^6[/latex].This is a standard difference of squares that can be rewritten as [latex](x^3)^2 + (8x^3)^2[/latex], which factors to [latex](x^3 - 8y^3)(x^3 + 8x^3)[/latex]. This is not completely factored yet, since both [latex](x^3 - 8y^3)[/latex] and [latex](x^3 + 8x^3)[/latex] can be factored again.
[latex](x^3-8y^3)=(x-2y)(x^2+2xy+y^2)[/latex] and [latex](x^3+8y^3)=(x+2y)(x^2-2xy+y^2)[/latex]
This means that the complete factorization for this is:
[latex]x^6 - 64y^6 = (x - 2y)(x^2 + 2xy + y^2)(x + 2y)(x^2 - 2xy + y^2)[/latex]
Example 7.6.3
A more challenging equation to factor looks like [latex]x^6 + 64y^6[/latex]. This is not an equation that can be put in the factorable form of a difference of squares. However, it can be put in the form of a sum of cubes.
[latex]x^6 + 64y^6 = (x^2)^3 + (4y^2)^3[/latex]
In this form, [latex](x^2)^3+(4y^2)^3[/latex] factors to [latex](x^2+4y^2)(x^4+4x^2y^2+64y^4)[/latex].
Therefore, [latex]x^6 + 64y^6 = (x^2 + 4y^2)(x^4 + 4x^2y^2 + 64y^4)[/latex].
Example 7.6.4
Consider encountering a sum and difference of squares question. These can be factored as follows: [latex](a + b)^2 - (2a - 3b)^2[/latex] factors as a standard difference of squares as shown below:
[latex](a+b)^2-(2a-3b)^2=[(a+b)-(2a-3b)][(a+b)+(2a-3b)][/latex]
Simplifying inside the brackets yields:
[latex][a + b - 2a + 3b] [a + b + 2a - 3b][/latex]
Which reduces to:
[latex][-a + 4b] [3a - 2b][/latex]
[latex](a + b)^2 - (2a - 3b)^2 = [-a - 4b] [3a - 2b][/latex]
Examples 7.6.5
Consider encountering the following difference of cubes question. This can be factored as follows:
[latex](a + b)^3 - (2a - 3b)^3[/latex] factors as a standard difference of squares as shown below:
[latex](a+b)^3-(2a-3b)^3[/latex] [latex]=[(a+b)-(2a+3b)][(a+b)^2+(a+b)(2a+3b)+(2a+3b)^2][/latex]
[latex][a+b-2a-3b][a^2+2ab+b^2+2a^2+5ab+3b^2+4a^2+12ab+9b^2][/latex]
Sorting and combining all similar terms yields:
[latex]\begin{array}{rrl} &[\phantom{-1}a+\phantom{0}b]&[\phantom{0}a^2+\phantom{0}2ab+\phantom{00}b^2] \\ &[-2a-3b]&[2a^2+\phantom{0}5ab+\phantom{0}3b^2] \\ +&&[4a^2+12ab+\phantom{0}9b^2] \\ \hline &[-a-2b]&[7a^2+19ab+13b^2] \end{array}[/latex]
Therefore, the result is:
[latex](a + b)^3 - (2a - 3b)^3 = [-a - 2b] [7a^2 + 19ab + 13b^2][/latex]
Completely factor the following equations.
- [latex]x^4-16y^4[/latex]
- [latex]16x^4-81y^4[/latex]
- [latex]x^4-256y^4[/latex]
- [latex]625x^4-81y^4[/latex]
- [latex]81x^4-16y^4[/latex]
- [latex]x^4-81y^4[/latex]
- [latex]625x^4-256y^4[/latex]
- [latex]x^6-y^6[/latex]
- [latex]x^6+y^6[/latex]
- [latex]x^6-64y^6[/latex]
- [latex]64x^6+y^6[/latex]
- [latex]729x^6-y^6[/latex]
- [latex]729x^6+y^6[/latex]
- [latex]729x^6+64y^6[/latex]
- [latex]64x^6-15625y^6[/latex]
- [latex](a+b)^2-(c-d)^2[/latex]
- [latex](a+2b)^2-(3a-4b)^2[/latex]
- [latex](a+3b)^2-(2c-d)^2[/latex]
- [latex](3a+b)^2-(a-b)^2[/latex]
- [latex](a+b)^3-(c-d)^3[/latex]
- [latex](a+3b)^3+(4a-b)^3[/latex]
Answer Key 7.6
Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.
Share This Book
Word Problems on Quadratic Equations by Factoring
We will learn how to solve Word Problems on quadratic equations by factoring.
1. The product of two numbers is 12. If their sum added to the sum of their squares is 32, find the numbers.
Let the numbers be x and y.
As their product is 12, we get xy = 12 ..................... (i)
According to the question, x + y + x\(^{2}\) + y\(^{2}\) = 32 ..................... (ii)
From (i), y = \(\frac{12}{x}\)
Putting y = \(\frac{12}{x}\) in (ii), we get
x + \(\frac{12}{x}\) + x\(^{2}\) + (\(\frac{12}{x}\))\(^{2}\) = 32
⟹ (x + \(\frac{12}{x}\)) + (x + \(\frac{12}{x}\))\(^{2}\) - 2 x ∙ \(\frac{12}{x}\) = 32
⟹ (x + \(\frac{12}{x}\))\(^{2}\) + (x + \(\frac{12}{x}\)) - 56 = 0
Putting x + \(\frac{12}{x}\) = t,
t\(^{2}\) + t - 56 = 0
⟹ t\(^{2}\) + 8t – 7t – 56 = 0
⟹ t(t + 8) - 7(t + 8) = 0
⟹ (t + 8)(t - 7) = 0
⟹ t + 8 = 0 or, t – 7 = 0
⟹ t = -8 or, t = 7
When t = -8,
x + \(\frac{12}{x}\) = t = -8
⟹ x\(^{2}\) + 8x + 12 = 0
⟹ x\(^{2}\) + 6x + 2x + 12 = 0
⟹ x(x + 6) + 2(x + 6) = 0
⟹ (x + 6)(x + 2) = 0
⟹ x + 6 = 0 or, x + 2 = 0
⟹ x = -6 or, x = -2
x + \(\frac{12}{x}\) = t = 7
⟹ x\(^{2}\) - 7x + 12 = 0
⟹ x\(^{2}\) - 4x - 3x + 12 = 0
⟹ x(x – 4) - 3(x – 4) = 0
⟹ (x - 4)(x - 3) = 0
⟹ x - 4 = 0 or, x - 3 = 0
⟹ x = 4 or 3
Thus, x = -6, -2, 4, 3
Then, the other number y = \(\frac{12}{x}\) = \(\frac{12}{-6}\) , \(\frac{12}{-2}\), \(\frac{12}{4}\), \(\frac{12}{3}\) = -2, -6, 3, 4.
Thus, the two numbers x, y are -6, -2, or -2, -6, or 4, 3 or 3, 4.
Therefore, the required two numbers are -6, -2 or 4, 3.
2. An association has a fund of $195. In addition that, each member of the association contributes the number of dollars equal to the number of members. The total money is divided equally among the members. If each of the members gets $ 28, find the number of members in the association.
Let the number of members be x.
Total contributions from them = $ x\(^{2}\) and the association has a fund of $ 195.
According to the problem,
x\(^{2}\) + 195 = 28x
⟹ x\(^{2}\) - 28x + 195 = 0
⟹ x\(^{2}\) - 15x - 13x + 195 = 0
⟹ x(x - 15) - 13(x - 15) = 0
⟹ (x - 15)(x - 13) = 0
Therefore, x = 15 or 13
There are 15 or 13 members in the association.
Note: Two answers are acceptable in this case.
Quadratic Equation
Introduction to Quadratic Equation
Formation of Quadratic Equation in One Variable
Solving Quadratic Equations
General Properties of Quadratic Equation
Methods of Solving Quadratic Equations
Roots of a Quadratic Equation
Examine the Roots of a Quadratic Equation
Problems on Quadratic Equations
Quadratic Equations by Factoring
Word Problems Using Quadratic Formula
Examples on Quadratic Equations
Worksheet on Formation of Quadratic Equation in One Variable
Worksheet on Quadratic Formula
Worksheet on Nature of the Roots of a Quadratic Equation
Worksheet on Word Problems on Quadratic Equations by Factoring
- 9th Grade Math
From Word Problems on Quadratic Equations by Factoring to HOME PAGE
Didn't find what you were looking for? Or want to know more information about Math Only Math . Use this Google Search to find what you need.
New! Comments
- Preschool Activities
- Kindergarten Math
- 1st Grade Math
- 2nd Grade Math
- 3rd Grade Math
- 4th Grade Math
- 5th Grade Math
- 6th Grade Math
- 7th Grade Math
- 8th Grade Math
- 10th Grade Math
- 11 & 12 Grade Math
- Concepts of Sets
- Probability
- Boolean Algebra
- Math Coloring Pages
- Multiplication Table
- Cool Maths Games
- Math Flash Cards
- Online Math Quiz
- Math Puzzles
- Binary System
- Math Dictionary
- Conversion Chart
- Homework Sheets
- Math Problem Ans
- Free Math Answers
- Printable Math Sheet
- Funny Math Answers
- Employment Test
- Math Patterns
- Link Partners
- Privacy Policy

Recent Articles
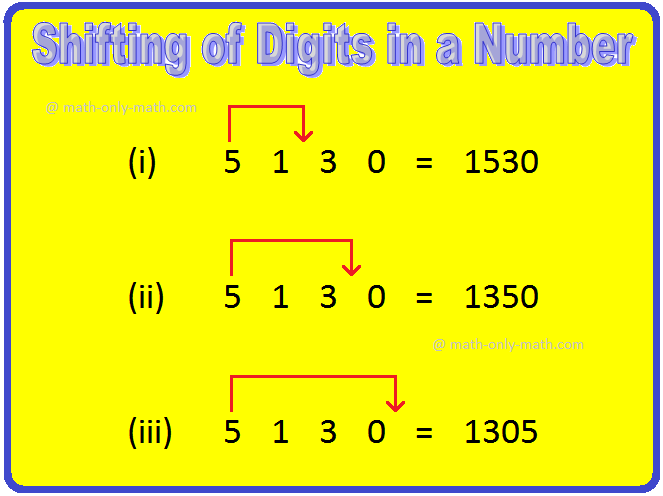
Shifting of Digits in a Number |Exchanging the Digits to Another Place
May 19, 24 06:35 PM
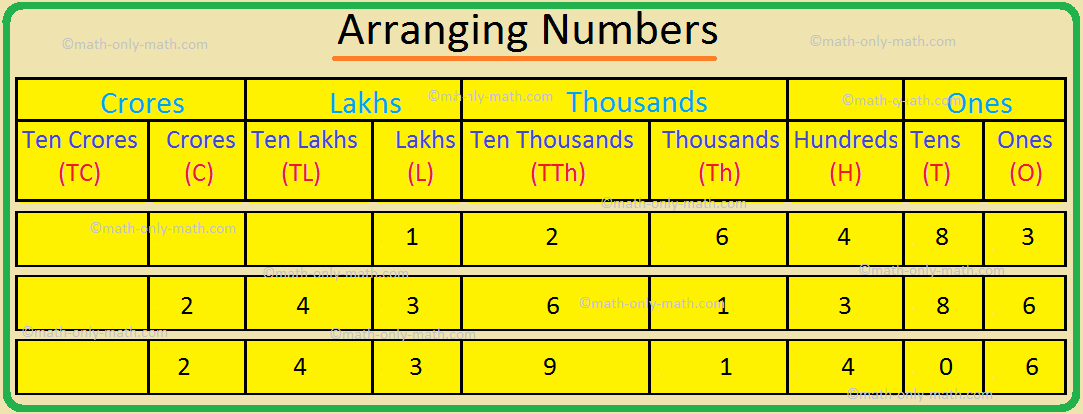
Formation of Greatest and Smallest Numbers | Arranging the Numbers
May 19, 24 03:36 PM

Formation of Numbers with the Given Digits |Making Numbers with Digits
May 19, 24 03:19 PM
Arranging Numbers | Ascending Order | Descending Order |Compare Digits
May 19, 24 02:23 PM
Comparison of Numbers | Compare Numbers Rules | Examples of Comparison
May 19, 24 01:26 PM

© and ™ math-only-math.com. All Rights Reserved. 2010 - 2024.
Mathematics 8 Quarter 1 – Module 2 Solving Problems Involving Factors of Polynomials
In this module, you will discover that the different methods of factoring can be used and applied in solving word problems. The scope of this material involves real-world encounters that can be defined mathematically using polynomial factoring. You are going to look at factoring at the real world and see how to solve word problems with reasonable solutions involving area, perimeter or finding two numbers that are consecutive values or create an equation that you are going to solve with accuracy and using variety of strategies.
This module contains:
Lesson 1- Solving Problems Involving Factors of Polynomials
After going through this module, you are expected to:
1. recall the different techniques of factoring polynomials;
2. apply the concept of factoring in solving related problems; and
3. describe the importance of understanding factoring and its application to real-life;
Can't Find What You'RE Looking For?
We are here to help - please use the search box below.
Leave a Comment Cancel reply

How Do You Solve a Word Problem by Factoring a Quadratic Equation?
- word problem
Background Tutorials
Introduction to algebraic expressions.

What is a Variable?
You can't do algebra without working with variables, but variables can be confusing. If you've ever wondered what variables are, then this tutorial is for you!
The Distributive Property

What is the Distributive Property?
The distributive property is a very deep math principle that helps make math work. It's the rule that lets you expand parentheses, and so it's really critical to understand if you want to get good at simplifying expressions. So check out the tutorial and let us know what you think!
Properties of Equality

What's the Subtraction Property of Equality?
Solving equations can be tough, especially if you've forgotten or have trouble understanding the tools at your disposal. One of those tools is the subtraction property of equality, and it lets you subtract the same number from both sides of an equation. Watch the video to see it in action!
Solving Polynomial Equations

What's the Zero Product Property?
The zero-product property let's you split the product of factors into separate equations. Then, you can solve each equation to get the solutions to your original equation! Learn all about this very useful property by watching this tutorial.
Solving Quadratics by Factoring
How Do You Solve a Quadratic Equation by Factoring?
One of the many ways you can solve a quadratic equation is by factoring it. In this tutorial, you'll see how to factor a quadratic equation using the guess and check method of factoring. Then, use the zero product property to find the solution!
- Terms of Use

- school Campus Bookshelves
- menu_book Bookshelves
- perm_media Learning Objects
- login Login
- how_to_reg Request Instructor Account
- hub Instructor Commons
Margin Size
- Download Page (PDF)
- Download Full Book (PDF)
- Periodic Table
- Physics Constants
- Scientific Calculator
- Reference & Cite
- Tools expand_more
- Readability
selected template will load here
This action is not available.

6.7: Applications Involving Quadratic Equations
- Last updated
- Save as PDF
- Page ID 23744

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
Learning Objectives
- Set up and solve applications involving relationships between real numbers.
- Set up and solve applications involving geometric relationships involving area and the Pythagorean theorem.
- Set up and solve applications involving the height of projectiles.
Number Problems
The algebraic setups of the word problems that we have previously encountered led to linear equations. When we translate the applications to algebraic setups in this section, the setups lead to quadratic equations. Just as before, we want to avoid relying on the “guess and check” method for solving applications. Using algebra to solve problems simplifies the process and is more reliable.
Example \(\PageIndex{1}\)
One integer is \(4\) less than twice another integer, and their product is \(96\). Set up an algebraic equation and solve it to find the two integers.
First, identify the variables. Avoid two variables by using the relationship between the two unknowns.
.png?revision=1)
The key phrase, “their product is \(96\),” indicates that we should multiply and set the product equal to \(96\).
\(n\cdot (2n-4)=96\)
Once we have the problem translated to a mathematical equation, we then solve. In this case, we can solve by factoring. The first step is to write the equation in standard form:
\(\begin{array} {cc} {n\cdot (2n-4)=96}&{\color{Cerulean}{Distribute\:n.}}\\{2n^{2}-4n=96}&{\color{Cerulean}{Subtract\:96\:from\:both\:sides.}}\\{2n^{2}-4n-96=0}&{} \end{array}\)
Next, factor completely and set each variable factor equal to zero.
\(\begin{array}{cc}{2n^{2}-4n-96=0}&{\color{Cerulean}{Factor\:out\:the\:GCF,\:2.}}\\{2(n^{2}-2n-48)=0}&{\color{Cerulean}{Factor\:the\:resulting\:trinomial.}}\\{2(n+6)(n-8)=0}&{\color{Cerulean}{Set\:each\:variable\:factor\:equal\:to\:zero.}} \end{array}\)
\(\begin{array}{ccc}{n+6=0}&{\text{or}}&{n-8=0}\\{n=-6}&{}&{n=8} \end{array}\)
The problem calls for two integers whose product is \(+96\). The product of two positive numbers is positive and the product of two negative numbers is positive. Hence we can have two sets of solutions. Use \(2n−4\) to determine the other integers.
\(\begin{array} {cc} {n=-6}&{n=8}\\{2n-4=2(\color{OliveGreen}{-6}\color{black}{)-4}}&{2n-4=2(\color{OliveGreen}{8}\color{black}{)-4}}\\{=-12-4}&{=16-4}\\{=-16}&{=12} \end{array}\)
Two sets of integers solve this problem: {\(8, 12\)} and {\(−6, −16\)}. Notice that \((8)(12) = 96\) and \((−6)(−16) = 96\); our solutions check out.
With quadratic equations, we often obtain two solutions for the identified unknown. Although it may be the case that both are solutions to the equation, they may not be solutions to the problem. If a solution does not solve the original application, then we disregard it.
Recall that consecutive odd and even integers both are separated by two units.
.png?revision=1)
Example \(\PageIndex{2}\)
- The product of two consecutive positive odd integers is \(99\). Find the integers.
Let \(n\) represent the first positive odd integer.
Let \(\color{OliveGreen}{n+2}\) represent the next positive odd integer.
The key phase, “product…is 99,” indicates that we should multiply and set the product equal to \(99\).
\(n\cdot (n+2)=99\)
Rewrite the quadratic equation in standard form and solve by factoring.
\(\begin{aligned} n^{2}+2n&=99 \\ n^{2}+2n-99&=0 \\ (n-9)(n+11)&=0 \end{aligned}\)
\(\begin{array}{ccc}{n-9=0}&{\text{or}}&{n+11=0}\\{n=9}&{}&{n=-11} \end{array}\)
Because the problem asks for positive integers, \(n=9\) is the only solution. Back substitute to determine the next odd integer.
\(\begin{aligned} n+2&=\color{OliveGreen}{9}\color{black}{+2} \\ &=11 \end{aligned}\)
The consecutive positive odd integers are \(9\) and \(11\).
Example \(\PageIndex{3}\)
Given two consecutive positive odd integers, the product of the larger and twice the smaller is equal to \(70\). Find the integers.
Let \(n\) represent the smaller positive odd integer.
Let \(n+2\) represent the next positive odd integer.
The key phrase “twice the smaller” can be translated to \(2n\). The phrase “product…is 70” indicates that we should multiply this by the larger odd integer and set the product equal to \(70\).
\((n+2)\cdot 2n=70\)
Solve by factoring.
\(\begin{array}{cc}{(n+2)\cdot 2n=70}&{\color{Cerulean}{Distribute.}}\\{2n^{2}+4n=70}&{\color{Cerulean}{Subtract\:70\:from\:both\:sides.}}\\{2n^{2}+4n-70=0}&{\color{Cerulean}{Factor\:out\:the\:GCF,\:2.}}\\{2(n^{2}+2n-35)=0}&{\color{Cerulean}{Factor\:the\:resulting\:trinomial.}}\\{2(n-5)(n+7)=0}&{\color{Cerulean}{Set\:each\:variable\:factor\:equal\:to\:zero.}} \end{array}\)
\(\begin{array}{ccc}{n-5=0}&{\text{or}}&{n+7=0}\\{n=5}&{}&{n=-7} \end{array}\)
Because the problem asks for positive integers, \(n=5\) is the only solution.
Back substitute into \(n + 2\) to determine the next odd integer.
\(\begin{aligned} n+2&=\color{OliveGreen}{5}\color{black}{+2}\\&=7 \end{aligned}\)
The positive odd integers are \(5\) and \(7\).
Exercise \(\PageIndex{1}\)
The product of two consecutive positive even integers is \(168\). Find the integers.
The positive even integers are \(12\) and \(14\).
Geometry Problems
When working with geometry problems, it is helpful to draw a picture. Below are some area formulas that you are expected to know. (Recall that \(π≈3.14\).)
Example \(\PageIndex{4}\)
The floor of a rectangular room has a length that is \(4\) feet more than twice its width. If the total area of the floor is \(240\) square feet, then find the dimensions of the floor.
.png?revision=1)
Use the formula \(A=l⋅w\) and the fact that the area is \(240\) square feet to set up an algebraic equation.
\(\begin{aligned} A&=l\cdot w \\ \color{OliveGreen}{240}&\color{black}{=(}\color{OliveGreen}{2w+4}\color{black}{)\cdot w} \end{aligned}\)
\(\begin{array} {ccc} {w-10=0}&{\text{or}}&{w+12=0} \\{w=10}&{}&{w=-12} \end{array}\)
At this point we have two possibilities for the width of the rectangle. However, since a negative width is not defined, choose the positive solution, \(w=10\). Back substitute to find the length.
\(\begin{aligned} 2w+4&=2(\color{OliveGreen}{10}\color{black}{)+4} \\ &=20+4 \\ &=24 \end{aligned}\)
The width is \(10\) feet and the length is \(24\) feet.
It is important to include the correct units in the final presentation of the answer. In the previous example, it would not make much sense to say the width is \(10\). Make sure to indicate that the width is \(10\) feet.
Example \(\PageIndex{5}\)
The height of a triangle is \(3\) inches less than twice the length of its base. If the total area of the triangle is \(7\) square inches, then find the lengths of the base and height.
.png?revision=1)
Use the formula \(A=\frac{1}{2}bh\) and the fact that the area is \(7\) square inches to set up an algebraic equation.
\(\begin{aligned} A&=\frac{1}{2} b\cdot h \\ \color{OliveGreen}{7}&\color{black}{=\frac{1}{2}b(\color{OliveGreen}{2b-3}\color{black}{)}} \end{aligned}\)
To avoid fractional coefficients, multiply both sides by \(2\) and then rewrite the quadratic equation in standard form.
Factor and then set each factor equal to zero.
\(\begin{array}{ccc}{2b-7=0}&{\text{or}}&{b+2=0}\\{2b=7}&{}&{b=-2}\\{b=\frac{7}{2}}&{}&{} \end{array}\)
In this case, disregard the negative answer; the length of the base is \(\frac{7}{2}\) inches long. Use \(2b−3\) to determine the height of the triangle.
The base measures \(\frac{7}{2} = 3\frac{1}{2}\) inches and the height is \(4\) inches.
The base of a triangle is \(5\) units less than twice the height. If the area is \(75\) square units, then what is the length of the base and height?
The height is \(10\) units and the base is \(15\) units.
Recall that a right triangle is a triangle where one of the angles measures \(90\)°. The side opposite of the right angle is the longest side of the triangle and is called the hypotenuse. The Pythagorean theorem gives us a relationship between the legs and hypotenuse of any right triangle, where \(a\) and \(b\) are the lengths of the legs and \(c\) is the length of the hypotenuse:
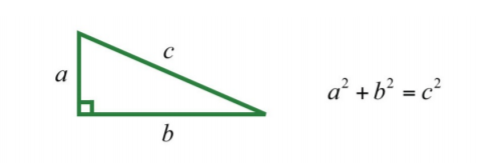.png?revision=1)
Given certain relationships, we use this theorem when determining the lengths of sides of right triangles.
Example \(\PageIndex{6}\)
The hypotenuse of a right triangle is \(10\) inches. If the short leg is \(2\) inches less than the long leg, then find the lengths of the legs.
.png?revision=1)
Given that the hypotenuse measures \(10\) inches, substitute its value into the Pythagorean theorem and obtain a quadratic equation in terms of \(x\).
\(\begin{aligned} a^{2}+b^{2}&=c^{2} \\ (\color{OliveGreen}{x-2}\color{black}{)^{2}+}\color{OliveGreen}{x}\color{black}{^{2}}&=\color{OliveGreen}{10}\color{black}{^{2}} \end{aligned}\)
Multiply and rewrite the equation in standard form.
\(\begin{aligned} (x-2)^{2}+x^{2}&=10^{2} \\ x^{2}-4x+4+x^{2}&=100 \\ 2x^{2}-4x-96&=0 \end{aligned}\)
Once it is in standard form, factor and set each variable factor equal to zero.
\(\begin{aligned} 2x^{2}-4x-96&=0\\ 2(x^{2}-2x-48)&=0 \\ 2(x+6)(x-8)&=0 \end{aligned}\)
\(\begin{array}{ccc}{x+6=0}&{\text{or}}&{x-8=0}\\{x=-6}&{}&{x=8} \end{array}\)
Because lengths cannot be negative, disregard the negative answer. In this case, the long leg measures \(8\) inches. Use \(x−2\) to determine the length of the short leg.
\(\begin{aligned} x-2&=\color{OliveGreen}{8}\color{black}{-2} \\ &=6 \end{aligned}\)
The short leg measures \(6\) inches and the long leg measures \(8\) inches.
Example \(\PageIndex{7}\)
One leg of a right triangle measures \(3\) centimeters. The hypotenuse of the right triangle measures \(3\) centimeters less than twice the length of the unknown leg. Find the measure of all the sides of the triangle.
.png?revision=1)
To set up an algebraic equation, we use the Pythagorean theorem.
\(\begin{aligned} a^{2}+b^{2}&=c^{2} \\ \color{OliveGreen}{3}\color{black}{^{2}+}\color{OliveGreen}{x}\color{black}{^{2}}&=(\color{OliveGreen}{2x-3}\color{black}{)^{2}} \end{aligned}\)
\(\begin{aligned} 3^{2}+x^{2}&=(2x-3)^{2} \\ 9+x^{2}&=4x^{2}-12x+9 \\ 0&=3x^{2}-12x \\ 0&=3x(x-4) \end{aligned}\)
\(\begin{array}{ccc}{3x=0}&{\text{or}}&{x-4=0}\\{x=0}&{}&{x=4} \end{array}\)
Disregard \(0\). The length of the unknown leg is \(4\) centimeters. Use \(2x−3\) to determine the length of the hypotenuse.
The sides of the triangle measure \(3\) centimeters, \(4\) centimeters, and \(5\) centimeters.
Exercise \(\PageIndex{2}\)
The hypotenuse of a right triangle measures \(13\) units. If one leg is \(2\) units more than twice that of the other, then find the length of each leg.
The two legs measure \(5\) units and \(12\) units.

Projectile Problems
The height of an object launched upward, ignoring the effects of air resistance, can be modeled with the following formula:
\[\text{height}=-\frac{1}{2}gt^{2}+v_{0}t+s_{0}\]
Using function notation, which is more appropriate, we have
\[h(t)=-\frac{1}{2}gt^{2}+v_{0}t+s_{0}\]
With this formula, the height can be calculated at any given time \(t\) after the object is launched. The coefficients represent the following:
We consider only problems where the acceleration due to gravity can be expressed as \(g=32\) ft/sec\(^{2}\). Therefore, in this section time will be measured in seconds and the height in feet. Certainly though, the formula is valid using units other than these.
Example \(\PageIndex{8}\)
The height of a projectile launched upward at a speed of \(32\) feet/second from a height of \(128\) feet is given by the function \(h(t)=−16t^{2}+32t+128\). How long does it take to hit the ground?
An inefficient method for finding the time to hit the ground is to simply start guessing at times and evaluating. To do this, construct a chart.
.png?revision=1)
Use the table to sketch the height of the projectile over time.
.png?revision=1)
We see that at \(4\) seconds, the projectile hits the ground. Note that when this occurs, the height is equal to \(0\). Now we need to solve this problem algebraically. To find the solution algebraically, use the fact that the height is \(0\) when the object hits the ground. We need to find the time, \(t\), when \(h(t)=0\).
\(h(t)=-16t^{2}+32t+128 \\ \color{Cerulean}{\downarrow} \\ 0 =-16t^{2}+32t+128\)
Solve the equation by factoring
\(\begin{aligned} 0 &=-16t^{2}+32t+128 \\ 0 &=-16(t^{2}-2t-8) \\ 0&=-16(t-4)(t+2) \end{aligned}\)
Now set each variable factor to zero.
\(\begin{array}{ccc}{t-4=0}&{\text{or}}&{t+2=0}\\{t=4}&{}&{t=-2} \end{array}\)
As expected, the projectile hits the ground at \(t=4\) seconds. Disregard \(−2\) as a solution because negative time is not defined.
The projectile hits the ground \(4\) seconds after it is launched.
Example \(\PageIndex{9}\)
The height of a certain book dropped from the top of a \(144\) foot building is given by \(h(t)=−16t^{2}+144\). How long does it take to hit the ground?
Find the time \(t\) when the height \(h(t)=0\).
\(\begin{aligned}0&=-16t^{2}+144 \\ 0&=-16(t^{2}-9) \\ 0&=-16(t+3)(t-3) \end{aligned}\)
\(\begin{array}{ccc}{t+3=0}&{\text{or}}&{t-3=0}\\{t=-3}&{}&{t=3} \end{array}\)
The book takes \(3\) seconds to hit the ground when dropped from the top of a \(144\)-foot building.
Exercise \(\PageIndex{3}\)
The height of a projectile, shot straight up into the air from the ground, is given by \(h(t)=−16t^{2}+80t\). How long does it take to come back down to the ground?
It will take 5 seconds to come back down to the ground.
Key Takeaways
- It is best to translate a word problem to a mathematical setup and then solve using algebra. Avoid using the “guess and check” method of solving applications in this section.
- When solving applications, check that your solutions make sense in the context of the question. For example, if you wish to find the length of the base of a triangle, then you would disregard any negative solutions.
- It is important to identify each variable and state in a sentence what each variable represents. It is often helpful to draw a picture.
Exercise \(\PageIndex{4}\) Number Problems
Set up an algebraic equation and then solve.
- One integer is five times another. If the product of the two integers is \(80\), then find the integers.
- One integer is four times another. If the product of the two integers is \(36\), then find the integers.
- An integer is one more than four times another. If the product of the two integers is \(39\), then find the integers.
- An integer is \(3\) more than another. If the product of the two integers is \(130\), then find the integers.
- An integer is \(2\) less than twice another. If the product of the two integers is \(220\), then find the integers.
- An integer is \(3\) more than twice another. If the product of the two integers is \(90\), then find the integers.
- One integer is \(2\) units more than another. If the product of the two integers is equal to five times the larger, then find the two integers.
- A positive integer is \(1\) less than twice another. If the product of the two integers is equal to fifteen times the smaller, then find the two integers.
- A positive integer is \(3\) more than twice a smaller positive integer. If the product of the two integers is equal to six times the larger, then find the integers.
- One positive integer is \(3\) more than another. If the product of the two integers is equal to twelve times the smaller, then find the integers.
- An integer is \(3\) more than another. If the product of the two integers is equal to \(2\) more than four times their sum, then find the integers.
- An integer is \(5\) more than another. If the product of the two integers is equal to \(2\) more than twice their sum, then find the integers.
- The product of two consecutive positive even integers is \(120\). Find the integers.
- The product of two consecutive positive integers is \(110\). Find the integers.
- The product of two consecutive positive integers is \(42\). Find the integers.
- The product of two consecutive positive odd integers is equal to \(1\) less than seven times the sum of the integers. Find the integers.
- The product of two consecutive positive even integers is equal to \(22\) more than eleven times the sum of the integers. Find the integers.
- The sum of the squares of two consecutive positive odd integers is \(74\). Find the integers.
- The sum of the squares of two consecutive positive even integers is \(100\). Find the integers.
- The sum of the squares of two consecutive positive integers is \(265\). Find the integers.
- The sum of the squares of two consecutive positive integers is \(181\). Find the integers.
- For two consecutive positive odd integers, the product of twice the smaller and the larger is \(126\). Find the integers.
- For two consecutive positive even integers, the product of the smaller and twice the larger is \(160\). Find the integers.
1. {\(4, 20\)} or {\(−4, −20\)}
3. \(3, 13\)
5. {\(11, 20\)} or {\(−22, −10\)}
7. {\(5, 7\)} or {\(−2, 0\)}
9. \(6, 15\)
11. {\(7, 10\)} or {\(−2, 1\)}
13. \(10, 12\)
15. \(10, 11\)
17. \(13, 15\)
19. \(5, 7\)
21. \(11, 12\)
23. \(7, 9\)
Exercise \(\PageIndex{5}\) Geometry Problems
- The width of a rectangle is \(7\) feet less than its length. If the area of the rectangle is \(170\) square feet, then find the length and width.
- The length of a rectangle is \(2\) feet more than its width. If the area of the rectangle is \(48\) square feet, then find the length and width.
- The width of a rectangle is \(3\) units less than the length. If the area is \(70\) square units, then find the dimensions of the rectangle.
- The width of a rectangle measures one half of the length. If the area is \(72\) square feet, then find the dimensions of the rectangle.
- The length of a rectangle is twice that of its width. If the area of the rectangle is \(72\) square inches, then find the length and width.
- The length of a rectangle is three times that of its width. If the area of the rectangle is \(75\) square centimeters, then find the length and width.
- The length of a rectangle is \(2\) inches more than its width. The area of the rectangle is equal to \(12\) inches more than three times the perimeter. Find the length and width of the rectangle.
- The length of a rectangle is \(3\) meters more than twice the width. The area of the rectangle is equal to \(10\) meters less than three times the perimeter. Find the length and width of the rectangle.
- A uniform border is to be placed around an \(8\)-inch-by-\(10\)-inch picture. If the total area including the border must be \(224\) square inches, then how wide should the border be?
.png?revision=1)
10. A \(2\)-foot brick border is constructed around a square cement slab. If the total area, including the border, is \(121\) square feet, then what are the dimensions of the slab?
11. The area of a picture frame including a \(2\)-inch wide border is \(99\) square inches. If the width of the inner area is \(2\) inches more than its length, then find the dimensions of the inner area.
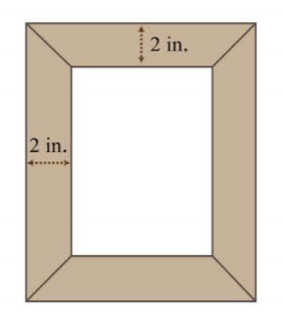.png?revision=1)
12. A box can be made by cutting out the corners and folding up the edges of a square sheet of cardboard. A template for a cardboard box with a height of \(2\) inches is given. What is the length of each side of the cardboard sheet if the volume of the box is to be \(50\) cubic inches?
.png?revision=1)
13. The height of a triangle is \(3\) inches more than the length of its base. If the area of the triangle is \(44\) square inches, then find the length of its base and height.
14. The height of a triangle is \(4\) units less than the length of the base. If the area of the triangle is \(48\) square units, then find the length of its base and height.
15. The base of a triangle is twice that of its height. If the area is \(36\) square centimeters, then find the length of its base and height.
16. The height of a triangle is three times the length of its base. If the area is \(73\frac{1}{2}\) square feet, then find the length of the base and height.
17. The height of a triangle is \(1\) unit more than the length of its base. If the area is \(5\) units more than four times the height, then find the length of the base and height of the triangle.
18. The base of a triangle is \(4\) times that of its height. If the area is \(3\) units more than five times the height, then find the length of the base and height of the triangle.
19. The diagonal of a rectangle measures \(5\) inches. If the length is \(1\) inch more than its width, then find the dimensions of the rectangle.
20. The diagonal of a rectangle measures \(10\) inches. If the width is \(2\) inches less than the length, then find the area of the rectangle.
21. If the sides of a right triangle are consecutive even integers, then what are their measures?
22. The hypotenuse of a right triangle is \(13\) units. If the length of one leg is \(2\) more than twice the other, then what are their lengths?
23. The shortest leg of a right triangle measures \(9\) centimeters and the hypotenuse measures \(3\) centimeters more than the longer leg. Find the length of the hypotenuse.
24. The long leg of a right triangle measures \(24\) centimeters and the hypotenuse measures \(4\) centimeters more three times the short leg. Find the length of the hypotenuse.
1. Length: \(17\) feet; width: \(10\) feet
3. Length: \(10\) units; width: \(7\) units
5. Length: \(12\) inches; width: \(6\) inches
7. Length: \(14\) inches; width: \(12\) inches
9. \(3\) inches
11. \(5\) inches by \(7\) inches
13. Base: \(8\) inches; height: \(11\) inches
15. Base: \(12\) centimeters; height: \(6\) centimeters
17. Base: \(9\) units; height: \(10\) units
19. \(3\) inches by \(4\) inches
21. \(6\) units, \(8\) units, and \(10\) units
23. \(15\) centimeters
Exercise \(\PageIndex{6}\) Projectile Problems
- The height of a projectile launched upward at a speed of \(32\) feet/second from a height of \(48\) feet is given by the function \(h(t)=−16t^{2}+32t+48. How long will it take the projectile to hit the ground?
- The height of a projectile launched upward at a speed of \(16\) feet/second from a height of \(192\) feet is given by the function \(h(t)=−16t^{2}+16t+192\). How long will it take to hit the ground?
- An object launched upward at a speed of \(64\) feet/second from a height of \(80\) feet. How long will it take the projectile to hit the ground?
- An object launched upward at a speed of \(128\) feet/second from a height of \(144\) feet. How long will it take the projectile to hit the ground?
- The height of an object dropped from the top of a \(64\)-foot building is given by \(h(t)=−16t^{2}+64\). How long will it take the object to hit the ground?
- The height of an object dropped from an airplane at \(1,600\) feet is given by \(h(t)=−16t^{2}+1,600\). How long will it take the object to hit the ground?
- An object is dropped from a ladder at a height of \(16\) feet. How long will it take to hit the ground?
- An object is dropped from a \(144\)-foot building. How long will it take to hit the ground?
- The height of a projectile, shot straight up into the air from the ground at \(128\) feet/second, is given by \(h(t)=−16t^{2}+128t\). How long does it take to come back down to the ground?
- A baseball, tossed up into the air from the ground at \(32\) feet/second, is given by \(h(t)=−16t^{2}+32t\). How long does it take to come back down to the ground?
- How long will it take a baseball thrown into the air at \(48\) feet/second to come back down to the ground?
- A football is kicked up into the air at \(80\) feet/second. Calculate how long will it hang in the air.
1. \(3\) seconds
3. \(5\) seconds
5. \(2\) seconds
7. \(1\) second
9. \(8\) seconds
11. \(3\) seconds
Exercise \(\PageIndex{7}\) Discussion Board Topics
- Research and discuss the life of Pythagoras.
- If the sides of a square are doubled, then by what factor is the area increased? Why?
- Design your own geometry problem involving the area of a rectangle or triangle. Post the question and a complete solution on the discussion board.
- Write down your strategy for setting up and solving word problems. Share your strategy on the discussion board.
1. Answers may vary
3. Answers may vary
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 3: Polynomial factorization
About this unit.
Let's get equipped with a variety of key strategies for breaking down higher degree polynomials. From taking out common factors to using special products, we'll build a strong foundation to help us investigate polynomial functions and prove identities.
Factoring monomials
- Introduction to factoring higher degree polynomials (Opens a modal)
- Introduction to factoring higher degree monomials (Opens a modal)
- Which monomial factorization is correct? (Opens a modal)
- Worked example: finding the missing monomial factor (Opens a modal)
- Worked example: finding missing monomial side in area model (Opens a modal)
- Factoring monomials (Opens a modal)
- Factor monomials Get 3 of 4 questions to level up!
Greatest common factor
- Greatest common factor of monomials (Opens a modal)
- Greatest common factor of monomials Get 3 of 4 questions to level up!
Taking common factors
- Taking common factor from binomial (Opens a modal)
- Taking common factor from trinomial (Opens a modal)
- Taking common factor: area model (Opens a modal)
- Factoring polynomials by taking a common factor (Opens a modal)
- Factor polynomials: common factor Get 3 of 4 questions to level up!
Factoring higher degree polynomials
- Factoring higher degree polynomials (Opens a modal)
- Factoring higher-degree polynomials: Common factor (Opens a modal)
- Factor higher degree polynomials Get 3 of 4 questions to level up!
Factoring using structure
- Identifying quadratic patterns (Opens a modal)
- Factorization with substitution (Opens a modal)
- Factoring using the perfect square pattern (Opens a modal)
- Factoring using the difference of squares pattern (Opens a modal)
- Identify quadratic patterns Get 3 of 4 questions to level up!
- Factorization with substitution Get 3 of 4 questions to level up!
- Factor polynomials using structure Get 3 of 4 questions to level up!
Polynomial identities
- Polynomial identities introduction (Opens a modal)
- Analyzing polynomial identities (Opens a modal)
- Describing numerical relationships with polynomial identities (Opens a modal)
- Polynomial identities Get 3 of 4 questions to level up!
Geometric series
- Geometric series introduction (Opens a modal)
- Finite geometric series formula (Opens a modal)
- Worked examples: finite geometric series (Opens a modal)
- Geometric series word problems: swing (Opens a modal)
- Geometric series word problems: hike (Opens a modal)
- Polynomial factorization: FAQ (Opens a modal)
- Geometric series formula Get 3 of 4 questions to level up!
- Finite geometric series word problems Get 3 of 4 questions to level up!
MAKE WAVES WITH THIS FREE WEEKLONG VOCABULARY UNIT!

Strategies for Solving Word Problems – Math

It’s one thing to solve a math equation when all of the numbers are given to you but with word problems, when you start adding reading to the mix, that’s when it gets especially tricky.
The simple addition of those words ramps up the difficulty (and sometimes the math anxiety) by about 100!
How can you help your students become confident word problem solvers? By teaching your students to solve word problems in a step by step, organized way, you will give them the tools they need to solve word problems in a much more effective way.
Here are the seven strategies I use to help students solve word problems.
1. read the entire word problem.
Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little better too.
2. Think About the Word Problem
Students need to ask themselves three questions every time they are faced with a word problem. These questions will help them to set up a plan for solving the problem.
Here are the questions:
A. what exactly is the question.
What is the problem asking? Often times, curriculum writers include extra information in the problem for seemingly no good reason, except maybe to train kids to ignore that extraneous information (grrrr!). Students need to be able to stay focused, ignore those extra details, and find out what the real question is in a particular problem.
B. What do I need in order to find the answer?
Students need to narrow it down, even more, to figure out what is needed to solve the problem, whether it’s adding, subtracting, multiplying, dividing, or some combination of those. They’ll need a general idea of which information will be used (or not used) and what they’ll be doing.
This is where key words become very helpful. When students learn to recognize that certain words mean to add (like in all, altogether, combined ), while others mean to subtract, multiply, or to divide, it helps them decide how to proceed a little better
Here’s a Key Words Chart I like to use for teaching word problems. The handout could be copied at a smaller size and glued into interactive math notebooks. It could be placed in math folders or in binders under the math section if your students use binders.
One year I made huge math signs (addition, subtraction, multiplication, and divide symbols) and wrote the keywords around the symbols. These served as a permanent reminder of keywords for word problems in the classroom.
If you’d like to download this FREE Key Words handout, click here:

C. What information do I already have?
This is where students will focus in on the numbers which will be used to solve the problem.
3. Write on the Word Problem
This step reinforces the thinking which took place in step number two. Students use a pencil or colored pencils to notate information on worksheets (not books of course, unless they’re consumable). There are lots of ways to do this, but here’s what I like to do:
- Circle any numbers you’ll use.
- Lightly cross out any information you don’t need.
- Underline the phrase or sentence which tells exactly what you’ll need to find.
4. Draw a Simple Picture and Label It
Drawing pictures using simple shapes like squares, circles, and rectangles help students visualize problems. Adding numbers or names as labels help too.
For example, if the word problem says that there were five boxes and each box had 4 apples in it, kids can draw five squares with the number four in each square. Instantly, kids can see the answer so much more easily!
5. Estimate the Answer Before Solving
Having a general idea of a ballpark answer for the problem lets students know if their actual answer is reasonable or not. This quick, rough estimate is a good math habit to get into. It helps students really think about their answer’s accuracy when the problem is finally solved.
6. Check Your Work When Done
This strategy goes along with the fifth strategy. One of the phrases I constantly use during math time is, Is your answer reasonable ? I want students to do more than to be number crunchers but to really think about what those numbers mean.
Also, when students get into the habit of checking work, they are more apt to catch careless mistakes, which are often the root of incorrect answers.
7. Practice Word Problems Often
Just like it takes practice to learn to play the clarinet, to dribble a ball in soccer, and to draw realistically, it takes practice to become a master word problem solver.
When students practice word problems, often several things happen. Word problems become less scary (no, really).
They start to notice similarities in types of problems and are able to more quickly understand how to solve them. They will gain confidence even when dealing with new types of word problems, knowing that they have successfully solved many word problems in the past.
If you’re looking for some word problem task cards, I have quite a few of them for 3rd – 5th graders.
This 3rd grade math task cards bundle has word problems in almost every one of its 30 task card sets..
There are also specific sets that are dedicated to word problems and two-step word problems too. I love these because there’s a task card set for every standard.
CLICK HERE to take a look at 3rd grade:

This 4th Grade Math Task Cards Bundle also has lots of word problems in almost every single of its 30 task card sets. These cards are perfect for centers, whole class, and for one on one.
CLICK HERE to see 4th grade:

This 5th Grade Math Task Cards Bundle is also loaded with word problems to give your students focused practice.
CLICK HERE to take a look at 5th grade:

Want to try a FREE set of math task cards to see what you think?
3rd Grade: Rounding Whole Numbers Task Cards
4th Grade: Convert Fractions and Decimals Task Cards
5th Grade: Read, Write, and Compare Decimals Task Cards
Thanks so much for stopping by!

- Read more about: Math
You might also like...

Fraction Activities Students Love – Math
Fractions can be tough! While it takes time and repeated exposure with fractions for students to have a real understanding of them, there are lots

Math Games Using Dice
Games are an important part of math class, in my opinion. Not only are kids able to practice the skills that we have been focusing

Math Games Using Dominoes
Math games have always been part of our math time. I love the fact that any time I introduce a math game, I know I’ll
Hi, I’m Jenn, CEO and owner of The Teacher Next Door!
I know that you strive to be an effective upper elementary teacher while maintaining a healthy work-life balance.
In order to do that, you need resources that are impactful, yet simple .
The problem is that most resources and curriculums out there are far from simple. The pages upon pages of daily lesson plans are just plain overwhelming .
At TTND, we believe teachers should be living their lives outside of the classroom, and not spend hours lesson planning and searching for resources.
We understand that now, more than ever, teachers need space to be themselves which is why we create and support teachers with timesaving tips and standards-aligned resources.
Want access to TTND's Free Resource Library? Sign up for our newsletter and we'll email you the exclusive password!
Trending posts.

SEARCH BY TOPIC
- Classroom Ideas
- Holidays and Seasonal
- Mentor Texts
- Reading Block
- Uncategorized
- Writing & Grammar
POPULAR RESOURCES

Facebook Group
Teachers Pay Teachers
Free Resource Library
💌 Contact Us
Disclosures
Privacy Policy
Refund Policy
Purchase Orders
Your Downloads
Reward Points
© The Teacher Next Door, LLC. All rights reserved.
* Please note: If your school has strong email filters, you may wish to use your personal email to ensure access.

COMMENTS
Solution. 1. Find the greatest common factor of the two terms. The greatest common factor of 12 and 30 is 6. 2. Keep the greatest common factor outside the brackets, divide the polynomial terms by this factor and write the remaining expression inside the brackets. (12x + 30) = (6 2x) + (6 5) 6 (2x + 5) 3.
going to look at factoring at the real world and see how to solve word problems with reasonable solutions involving area, perimeter or finding two numbers that are consecutive values or create an equation that you are going to solve with accuracy and using variety of strategies. This module contains: Lesson 1- Solving Problems Involving Factors ...
Finding Distances and Time Traveled using Polynomials. So, together we are going to look at factoring in the real world, and see how to solve word problems involving area and perimeter, height, speed, and distance. But it is important to note that while these problems lead to polynomial equations that can be solved by factoring, not all ...
Solution: Since the "widest" and "split things" concepts are present, this is a GCF problem. Using prime factorization on 84 and 96, find the GCF: 84 = 2 x 2 x 3 x 7. 96 = 2 x 2 x 2 x 2 x 2 x 3. GCF = 2 x 2 x 3 = 12. Kyle should cut each tarp into 12 inch widths. FYI: If you look at 84 + 96 = 12 (7 + 8)
7.6 Factoring Quadratics of Increasing Difficulty. Factoring equations that are more difficult involves factoring equations and then checking the answers to see if they can be factored again. Factor y4 −81x4 y 4 − 81 x 4. This is a standard difference of squares that can be rewritten as (y2)2 − (9x2)2 ( y 2) 2 − ( 9 x 2) 2, which ...
Yes. The first term is a perfect square since 4 x 2 = ( 2 x) 2 , and the last term is a perfect square since 9 = ( 3) 2 . Also, the middle term is twice the product of the numbers that are squared since 12 x = 2 ( 2 x) ( 3) . We can use the perfect square trinomial pattern to factor the quadratic. = 4 x 2 + 12 x + 9 = ( 2 x) 2 + 2 ( 2 x) ( 3 ...
Quadratic word problems (factored form) Google Classroom. You might need: Calculator. Ricardo throws a stone off a bridge into a river below. The stone's height (in meters above the water), x seconds after Ricardo threw it, is modeled by. w ( x) = − 5 ( x − 8) ( x + 4)
the factored expression is ( x + 2) ( x − 5) . The complete solution of the equation would go as follows: x 2 − 3 x − 10 = 0 ( x + 2) ( x − 5) = 0 Factor. ↙ ↘ x + 2 = 0 x − 5 = 0 x = − 2 x = 5. Now it's your turn to solve a few equations on your own. Keep in mind that different equations call for different factorization methods.
How to use a problem solving strategy to solve word problems. Read the problem. Make sure all the words and ideas are understood. Identify what we are looking for. Name what we are looking for. Choose a variable to represent that quantity. Translate into an equation. It may be helpful to restate the problem in one sentence with all the ...
Solutions for Solving Word Problems using Factoring. 1. The product of two consecutive integers is 272. Find the value of each integer. The first thing you need to do is to define the integers. Let n = the first integer Let n+1 = the 2nd integer. The product means to multiply so we need to multiply the two integers together.
Word Problems on Quadratic Equations by Factoring. We will learn how to solve Word Problems on quadratic equations by factoring. 1. The product of two numbers is 12. If their sum added to the sum of their squares is 32, find the numbers. Solution: Let the numbers be x and y.
Use a problem solving strategy to solve word problems. Step 1. Read the problem. Make sure all the words and ideas are understood. Step 2. Identify what we are looking for. Step 3. Name what we are looking for. Choose a variable to represent that quantity. Step 4. Translate into an equation. It may be helpful to restate the problem in one ...
You are going to look at factoring at the real world and see how to solve word problems with reasonable solutions involving area, perimeter or finding two numbers that are consecutive values or create an equation that you are going to solve with accuracy and using variety of strategies.
Additionally, notice that the middle term is two times the product of the numbers that are squared: 2 ( x) ( 4) = 8 x . This tells us that the polynomial is a perfect square trinomial, and so we can use the following factoring pattern. a 2 + 2 a b + b 2 = ( a + b) 2. In our case, a = x and b = 4 . We can factor our polynomial as follows: x 2 ...
One of the many ways you can solve a quadratic equation is by factoring it. In this tutorial, you'll see how to factor a quadratic equation using the guess and check method of factoring. Then, use the zero product property to find the solution! Virtual Nerd's patent-pending tutorial system provides in-context information, hints, and links to ...
Design your own geometry problem involving the area of a rectangle or triangle. Post the question and a complete solution on the discussion board. Write down your strategy for setting up and solving word problems. Share your strategy on the discussion board. Answer. 1. Answers may vary. 3. Answers may vary
ShowHide Resources. Apply quadratic factoring techniques to solve real-world problems.
About this unit. Let's get equipped with a variety of key strategies for breaking down higher degree polynomials. From taking out common factors to using special products, we'll build a strong foundation to help us investigate polynomial functions and prove identities.
Here are the seven strategies I use to help students solve word problems. 1. Read the Entire Word Problem. Before students look for keywords and try to figure out what to do, they need to slow down a bit and read the whole word problem once (and even better, twice). This helps kids get the bigger picture to be able to understand it a little ...
Considering the difficulties students face when solving word problems, a paucity of studies (e.g., Brack, 2020) has recommended a potential mnemonic problem-solving strategy that fosters deep knowledge and skills in solving word problems.This study examines the effectiveness of the KNOWS strategy (K—Know, N—Need to know, O—Organize, W—Work, and S—Solution) as a mnemonic approach in ...
factoring at the real world and see how to solve word problems with reasonable solutions involving area, perimeter or finding two numbers that are consecutive values or create an equation that you are going to solve with accuracy and using variety of strategies. This module contains: Lesson 1- Solving Problems Involving Factors of Polynomials ...
<iframe src="//www.googletagmanager.com/ns.html?id=GTM-NFJ3V2" height="0" width="0" style="display: none; visibility: hidden" ></iframe >