equilibrium of rigid bodies solved problems

12.5: Rigid Body Equilibrium Problems - I

Chapter 1: units, dimensions, and measurements, chapter 2: vectors and scalars, chapter 3: motion along a straight line, chapter 4: motion in two or three dimensions, chapter 5: newton's laws of motion, chapter 6: application of newton's laws of motion, chapter 7: work and kinetic energy, chapter 8: potential energy and energy conservation, chapter 9: linear momentum, impulse and collisions, chapter 10: rotation and rigid bodies, chapter 11: dynamics of rotational motions, chapter 12: equilibrium and elasticity, chapter 13: fluid mechanics, chapter 14: gravitation, chapter 15: oscillations, chapter 16: waves, chapter 17: sound, chapter 18: temperature and heat, chapter 19: the kinetic theory of gases, chapter 20: the first law of thermodynamics, chapter 21: the second law of thermodynamics, chapter 22: electric charges and fields, chapter 23: gauss's law, chapter 24: electric potential, chapter 25: capacitance, chapter 26: current and resistance, chapter 27: direct-current circuits, chapter 28: magnetic forces and fields, chapter 29: sources of magnetic fields, chapter 30: electromagnetic induction, chapter 31: inductance, chapter 32: alternating-current circuits, chapter 33: electromagnetic waves.

The JoVE video player is compatible with HTML5 and Adobe Flash. Older browsers that do not support HTML5 and the H.264 video codec will still use a Flash-based video player. We recommend downloading the newest version of Flash here, but we support all versions 10 and above.

For a rigid body to be in equilibrium, the net force and the net torque acting on it must be equal to zero. Solving a rigid body equilibrium problem typically involves three main steps.

Step one, create an idealized model of the object by separating it from its surroundings.

In the second step, draw a free-body diagram depicting all the applied forces on the system and identify the unknown to be determined.

Finally, select a coordinate axis and specify the positive direction of rotation due to the acting torques. Additionally, choose a reference point about which to calculate the net torque.

Apply the equations of equilibrium and substitute the values to solve for the unknown.

A rigid body is said to be in static equilibrium when the net force and the net torque acting on the system is equal to zero. To solve for rigid body equilibrium problems, do the following steps.

Step 1: Identify the object to be analyzed and all forces acting on the object. In addition, identify the known and unknown variables in the given problem.
Step 2: Set up a free-body diagram for the object. Choose the xy -reference frame for the problem. Draw a free-body diagram of the object, including only the forces that act on it. Label all forces in the x- and y -directions. For an unknown force, the direction must be assigned arbitrarily, that is, as a working direction. A plus sign (+) means that the working direction is the actual direction. A minus sign (−) means that the actual direction is opposite to the assumed working direction. Also, choose the location of the pivot point with respect to which all the forces are computed.
Step 3. Set up the equations of equilibrium for the object. Use the free-body diagram to write a correct equilibrium condition for the force and torque components in the x - y direction and along the axis of rotation, respectively
Step 4. Simplify and solve the system of equations for equilibrium to obtain unknown quantities. The number of equations should be the same as the number of unknowns. Then, evaluate the expressions for the unknown quantities.

This text is adapted from Openstax, University Physics Volume 1, Section 12.2: Examples of Static Equilibrium.

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

mktb-description

We use cookies to enhance your experience on our website.

By continuing to use our website or clicking “Continue”, you are agreeing to accept our cookies.

Engineering Statics: Open and Interactive

(5 reviews)

Daniel W. Baker, Colorado State University

William Haynes, Massachusetts Maritime Academy

Publisher: Daniel Baker and William Haynes

Language: English

Formats Available

Conditions of use.

Learn more about reviews.

Reviewed by Mohammad Valipour, Assistant Professor, Metropolitan State University of Denver on 8/28/23

Comprehensiveness rating: 4 see less

I found this book very interesting and thorough. Fortunately, the book covers most of the syllabus for Statics courses that I teach. The order of the chapters is also logical and in a standard form including Introduction to Statics, Forces and Other Vectors, Equilibrium of Particles, Moments and Static Equivalence, Rigid Body Equilibrium, Equilibrium of Structures, Centroids and Centers of Gravity, Internal Forces, Friction, and Moments of Inertia. There are interactive problems at the end of each chapter of the book which can be considered as a quick review of the book. Also, I found the trigonometric tables very useful for students who have forgotten basic geometry and trigonometry. One of the interesting parts of this book is using QR codes for which you can have access to dynamic pictures of the book. The only negative point that I can mention is the lack of enough sample problems for each content. Students who take Engineering Statics need to practice many problems/examples to get ready for their exams. Only one sample problem for most of the topics is not enough particularly for those who need time to understand the concepts through solving sample problems. I think students can use this book as a study guide very well but they also need an auxiliary textbook/pamphlet to fill the gap of not solving multiple problems for each topic. Adding an index/glossary is also helpful.

Content Accuracy rating: 5

In the current format, the book looks accurate. I could not find any problem with a wrong answer neither in the solution nor in the final answers.

Relevance/Longevity rating: 5

I found the relevancy aspect of this book pretty high. Since the topics rely on the fundamentals of physics and follow Euclidean geometry, we cannot expect any change in the near future. However, the authors try to stay up to date by using matrix solutions which is highly appreciated. In addition, the users can take advantage of the graphical solutions if they use technology such as GeoGebra or a CAD program to make the diagram, then their answers will be precise.

Clarity rating: 4

Using subsections facilitates the readability aspect of the book. Supporting graphs are also useful. Thinking Deeper sections are also interesting for those students who want to know more about the concepts behind the problems. I like the friendly tone that has been used by the authors and the vocabulary and terminology are understandable for all readers even international students. Using more colorful figures may be attractive for students who are less interested in engineering problems.

Consistency rating: 4

This is my favorite part of this book. It is very consistent and readable like a story from chapter 1 to chapter 10. The overall structure of the book holds together quite well. I like that figures in each chapter have their own numbering system with respect to the chapter number. However, figure captions look too short, and adding some more information may be useful.

Modularity rating: 5

There are 10 chapters in this book. The author has done a nice job by putting sections and subsections in the right place. Different parts of the text are useable to be presented to students in different topics which might not be even the same in the book. The book includes occasional references to other subsections for further information, but such self-references do not look disruptive.

Organization/Structure/Flow rating: 5

I think the material is provided and put together realistically. The organization of this book is logical. The sections and even subsections flow easily together with the previous and following sections/subsections. I like the idea of using key questions at the beginning of each chapter. This book is organized and follows a clear structure. Each chapter starts with a chapter description and a list of sections. I found the online version of the book flow better due to the interactive design. The PDF version is also well formatted. Also, the topics are presented in a short concise fashion.

Interface rating: 5

An advantage of this book is having a user-friendly interface which makes it much easier for students to follow up with the materials discussed in the book. Unlike many other OER books, the PDF version does look like a regular book. In my opinion, the navigation of the book is easy for both the PDF version and the online version. All figures and graphs are clear and readable. The sections and subsections are loaded quickly, and the figures and diagrams can be loaded without any issues.

Grammatical Errors rating: 5

I could not find any grammatical errors in the book.

Cultural Relevance rating: 4

I did not find the book offensive/insensitive in any way. It would be better to cover more examples from different parts of the world to be fairer for international readers/students.

Reviewed by James Book, Assistant Instructional Professor, Pittsburg State University on 12/15/22

This text covers most all topics under the statics umbrella with the notable exception of virtual work. The end of chapter interactive problem sets are excellent and make for a good review of the topics covered. The option to "randomize" each problem is a great help in exam preparation. The back matter covers useful trigonometric functions and provides handy steel sections tables.

I found no obvious errors or biases in the text. The back matter equations and reference tables are accurate.

The basic principles of statics covered by this text will remain relevant for a very long time. The end of chapter problem "randomization" feature will provide fresh challenges to the student and teacher. The prose used in writing the text is modern and up to date. Since it is provided on-line, the text should be relatively easy to keep current.

Clarity rating: 5

The text is written in an easy-to-read style with a fairly basic vocabulary. The technical terms used are well explained. The illustrations are adequate but could be expanded to include some simple video content. A feature to vary the font type and size would make the text more accessible. The use of color in many of the illustrations helps with clarity. The method of concealing the answer and solution guides to the example problems is clever.

Consistency rating: 5

The text follows a consistent, repeated pattern throughout. The presentation of each topic adequately builds on ideas and concepts from previous chapters. The overall structure of the text holds together well.

The text is divided into very manageable segments that can stand on their own. It does not appear to be overly self-referential. There are no enormous blocks of text or sections that run-on unnecessarily.

The text is well organized with deliberate and logical progression through statics concepts. The on-line version of the text seems to flow better due to the interactive design, but both on-line and pdf versions are well organized.

Both the on-line and pdf versions of the text provide easy and clear navigation. A check of several of the text hyperlinks showed accurate navigation. Charts, graphs, and other images were clear and readable.

No obvious grammatical errors were encountered.

Cultural Relevance rating: 5

The topic of statics does not lend itself to much discussion of cultural topics. The examples used in the text were generic and did not seem to be culturally biased, offensive, or insensitive.

Reviewed by Michael Pastor, Assistant Professor, Tidewater Community College on 11/27/22

A fully hyperlinked and intuitive table of contents is available for this text. I could find no index, however, the PDF version is searchable, and a search bar exists in the browser edition. For the most part, this text covers all topics normally associated with a typical engineering undergraduate class in mechanics dealing with the state of bodies at rest. The text begins with Newton's Laws, Forces, and Vectors, then moves on to the analysis of particles and rigid bodies. The text also includes chapters on centroids and moments of inertia, as well as chapters on internal loading and friction. A section on virtual work and energy methods is however, missing.

I have not noticed in inaccuracies and have used this text as an optional online resource in my sophomore level statics class for a number of semesters now. Students have never reported any issues.

The relevance for this text is quite high. The material presented here has not changed in at least the last 4 decades. The online mode of delivery, however, is quite refreshing and a relative new achievement. This text is licensed under CC Attribution-Non Commercial-Share Alike.

Chapters are divided into sections and the information is brief and to the point. Occasionally supporting graphics are presented and these can be easily magnified. Very little time is spent on derivation or formulation of relationships presented. However, occasionally extra "thinking deeper" information is presented at a mouse click. Here optional background information is presented on certain subjects. There are some example problems associated with topics and these are somewhat interactive... usually involving showing an answer then showing a more detailed solution on mouse click . Occasionally, there is an interactive diagram demonstrating some concept visually. However, I did not always find these intuitive, and in some cases did not understand how to effectively manipulate them.

I did not notice any inconsistencies in terminology or framework. The work is authored in PreTeXt and powered by MathJax. I have always found it quite easy to navigate chapters and sections consistently in this text. However, I have never tried using it on a cell phone or pad. In the appendix, there is a notation chapter outlining many if not all symbols used in the text.

Modularity rating: 4

The text is divided into chapters (common to most texts of this type). Each chapter is then broken down into sections. An appendix with math formulas and steel section properties is also included. This helps comply with ABET standards. I, however, could not locate simple shape properties in any tables or diagrams either in the chapters or appendices.

Organization/Structure/Flow rating: 4

The topics are present is a short concise fashion. This in my opinion is appropriate for an online resource. However, I would like to see the availability of more details concerning the derivation and/or development of some concepts and equations. Perhaps this could be added in optional user interactive sections.

Navigation of chapters, sections, and pages is quite easy and intuitive for this text. Some of the interactive diagrams were confusing and not well explained. A search bar is available to help locate specific ideas. However, this material is so consistently organized that navigation with the interactive Contents menu is all that I have ever needed.

I saw no issues here.

I noticed no insensitive or offensive areas in this text.

I have used this text for a number of semesters as a secondary resource for students in my engineering static classes. I think it would also work well as an instructor resource. The license allows for it to be upgraded and specialized to a users needs in a non-commercial and open way.

Reviewed by Anahita Khodadadi, Assistant Professor, Portland State University on 6/22/22

The textbook covers the fundamental concepts of statics including, force and vector analysis, equilibrium, internal reactions, and geometrical properties. The textbook also includes required steel section tables and a review of trigonometry principles. I would suggest this textbook in combination with a textbook on basics of mechanics and material properties to students who seek learning about basic concepts of engineering design.

To the best of my understanding the content of the textbook and the interactive exercises look accurate, unbiased, and thorough.

The textbook contains basic principles of statics which are not expected to be changed unless a groundbreaking theory in physics emerges in the future! The text itself is arranged in a way that can easily be edited and extended. I appreciate the efforts that the author has made to create and embed the interactive diagrams and exercises within the textbook instead of inserting the link of available items across different references. This will maintain the configuration of the textbook in the long term.

The text is written in a friendly tone and even students’ presumptions and concerns are early discussed in first chapters. Technical terms are well explained for those who may not have any background in engineering. In the future, the author may include relevant videos to the textbook as well to enhance the clarity of the materials and better engage audio-visual learners.

The text and even visuals are consistent in terms of terminology, format, and graphics. All figures are numbered and mentioned within the text.

The textbook is appropriately organized in 10 chapters. Each chapter is explained in multiple subsections that allow readers focusing on small chunks of learning materials. The text includes occasional references to other subsections for further information but such self-references do not look disruptive.

Both online and PDF version of the book are presented in a fine, clear and logical fashion. The online version allows easy navigation between different sections and subsections. The PDF version is also clearly formatted. It is helpful that each chapter begins with a series of key questions and ends with a number of exercises.

I reviewed the online version both on a computer and smartphone. The interface looks fine on a computer but on a smartphone some of the interactive diagrams cannot be displayed. However, I think students may rarely use a smartphone as a primary means of accessing the textbook.

The textbook looks well proofed.

The textbook is focused on math and physics and doesn’t discuss culturally sensitive topics. Examples intrinsically do not have the capacity to demonstrate diversity and inclusion matters.

Reviewed by Peter Kazarinoff, Professor, Portland Community College on 12/16/21

Comprehensiveness rating: 5 see less

The topics covered in a typical college Engineering Statics course are present. The chapters follow a common Statics textbook pattern of concepts, starting with forces and particles and ending with friction and moments of inertia. Chapter 6 includes the method of cuts and the method of joints. The only thing that many commercial Statics textbooks have compared to this book is an extensive number of problems at the end of each chapter (the fiction chapter, in particular, had few practice problems) and more reference material at the end of the book such as the centroid of common shapes. What this book has that those commercial books lack are interactive problems.

To the best of my knowledge, the content in the book is accurate. The interactive problems I attempted showed the same auto-generated answer as I recorded using pencil and paper. The equations seem accurate throughout. The reference material at the end of the book which contains things like trig identities and properties of steel sections seems accurate.

The fundamentals of Engineering Statics, like introductory Physics and Chemistry, have not changed in a decade. So the content in the book is relevant to a current Statics course and will be relevant to future Statics classes. The only reason the book could become dated is that the interactive animations and interactive problems are no longer supported by new web browsers or new web browsing tools that I can’t even imagine will be in place in 10 years. The book has a pdf version that can be printed.

The clarity of the writing is high, the font and spacing are easy to read. The book is written in a formal academic style which is clear but can seem terse. The diagrams in the book are easy to read and use a common style to show forces, angles, and geometry.

The book is consistent from chapter to chapter and the formatting is consistent from chapter to chapter. The book has a clear numbering system for chapters, sections, and subsections. Each of the diagrams and pictures in the book follows the same captioning format. Equations in the book are formatted consistently and labeled in the same way. Each section within a chapter in the book contains a set of “key questions” that section addresses.

The book is broken up into chapters and each chapter is broken down into sections. A typical quarter or semester-long Statics course would cover almost all of the book. It would be possible to only cover a few chapters. These chapters would need to start at the beginning of the book. It wouldn’t make sense to try and pull out just the middle or end chapters as the material in the book builds up chapter to chapter. One way the book could be used is to just assign the interactive problems for practice.

This book is organized and follows a clear structure. Each chapter starts with a chapter description and a list of sections. Each section starts with “Key Questions” and then proceeds with the section content. There are interactive problems at the end of each chapter.

Interface rating: 4

The online book interface is easy to navigate. Each chapter and section is clickable and it is easy to determine which part of the book you are reading. The sections load quickly and the images, diagrams, and interactive problems load without issue. In particular, the interactive problems are pretty slick. The only reason I don’t rate the interface as a 5 is that there is no search function. I don’t know how hard it would be to add a search bar to the online version of the book, but I do think a search function would be helpful. On my device, the book only took up the left half of my screen. This may be related to the browser/device I use, but in my reading, it seems like half of the screen real estate is wasted and a lot of scrolling is needed.

No grammatical or structural errors were found. The book seems to be free of typos and seems well-proofed. There also don’t seem to be any formatting inconsistencies chapter to chapter or section to section.

Cultural Relevance rating: 3

From what I read, I didn't notice any insensitive or offensive passages in the book. However, the lens of diversity and cultural relevance is not addressed in this book. Some of the pictures in the book depicting statics topics cover common “male-dominated” examples such as motorcycles, and football training sleds.

This is a well-written, high-quality, and organized book. It is a great resource for both instructors and students in undergraduate courses in Engineering Statics. For our needs, at a community college with a 2-year program in Mechanical Engineering and Civil Engineering, this book is a good alternative to commercial offerings from Pearson or McGraw-Hill. It’s a high-quality and interesting book with fantastic interactive problems. The only knock against it is that there could be more worked examples and problems at the end of each chapter for student practice.

1 Introduction to Statics
2 Forces and Other Vectors
3 Equilibrium of Particles
4 Moments and Static Equivalence
5 Rigid Body Equilibrium
6 Equilibrium of Structures
7 Centroids and Centers of Gravity
8 Internal Loadings
10 Moments of Inertia

Ancillary Material

Daniel Baker and William Haynes

About the Book

Engineering Statics is a free, open-source textbook appropriate for anyone who wishes to learn more about vectors, forces, moments, static equilibrium, and the properties of shapes. Specifically, it has been written to be the textbook for Engineering Mechanics: Statics, the first course in the Engineering Mechanics series offered in most university-level engineering programs.

This book’s content should prepare you for subsequent classes covering Engineering Mechanics: Dynamics and Mechanics of Materials. At its core, Engineering Statics provides the tools to solve static equilibrium problems for rigid bodies. The additional topics of resolving internal loads in rigid bodies and computing area moments of inertia are also included as stepping stones for later courses. We have endeavored to write in an approachable style and provide many questions, examples, and interactives for you to engage with and learn from.

About the Contributors

Daniel W. Baker , Colorado State University

William Haynes , Massachusetts Maritime Academy

Contribute to this Page

EN - English

DE - Deutsch

ES - Español

IT - Italiano

FR - Français

PT - Português

Table of content

Full table of contents

A rigid body is said to be in static equilibrium when the net force and the net torque acting on the system is equal to zero. To solve for rigid body equilibrium problems, do the following steps.

Step 1: Identify the object to be analyzed and all forces acting on the object. In addition, identify the known and unknown variables in the given problem.
Step 2: Set up a free-body diagram for the object. Choose the xy -reference frame for the problem. Draw a free-body diagram of the object, including only the forces that act on it. Label all forces in the x- and y -directions. For an unknown force, the direction must be assigned arbitrarily, that is, as a working direction. A plus sign (+) means that the working direction is the actual direction. A minus sign (−) means that the actual direction is opposite to the assumed working direction. Also, choose the location of the pivot point with respect to which all the forces are computed.
Step 3. Set up the equations of equilibrium for the object. Use the free-body diagram to write a correct equilibrium condition for the force and torque components in the x - y direction and along the axis of rotation, respectively
Step 4. Simplify and solve the system of equations for equilibrium to obtain unknown quantities. The number of equations should be the same as the number of unknowns. Then, evaluate the expressions for the unknown quantities.

This text is adapted from Openstax, University Physics Volume 1, Section 12.2: Examples of Static Equilibrium.

Recommend to library

JoVE NEWSLETTERS

JoVE Journal

Methods Collections

JoVE Encyclopedia of Experiments

JoVE Science Education

JoVE Lab Manual

Faculty Resource Center

Publishing Process

Editorial Board

Scope and Policies

Peer Review

Testimonials

Subscriptions

Library Advisory Board

12.2 Examples of Static Equilibrium

Learning objectives.

By the end of this section, you will be able to:

Identify and analyze static equilibrium situations
Set up a free-body diagram for an extended object in static equilibrium
Set up and solve static equilibrium conditions for objects in equilibrium in various physical situations

All examples in this chapter are planar problems. Accordingly, we use equilibrium conditions in the component form of Equation 12.7 to Equation 12.9 . We introduced a problem-solving strategy in Example 12.1 to illustrate the physical meaning of the equilibrium conditions. Now we generalize this strategy in a list of steps to follow when solving static equilibrium problems for extended rigid bodies. We proceed in five practical steps.

Problem-Solving Strategy

Static equilibrium.

Identify the object to be analyzed. For some systems in equilibrium, it may be necessary to consider more than one object. Identify all forces acting on the object. Identify the questions you need to answer. Identify the information given in the problem. In realistic problems, some key information may be implicit in the situation rather than provided explicitly.
Set up a free-body diagram for the object. (a) Choose the xy -reference frame for the problem. Draw a free-body diagram for the object, including only the forces that act on it. When suitable, represent the forces in terms of their components in the chosen reference frame. As you do this for each force, cross out the original force so that you do not erroneously include the same force twice in equations. Label all forces—you will need this for correct computations of net forces in the x - and y -directions. For an unknown force, the direction must be assigned arbitrarily; think of it as a ‘working direction’ or ‘suspected direction.’ The correct direction is determined by the sign that you obtain in the final solution. A plus sign ( + ) ( + ) means that the working direction is the actual direction. A minus sign ( − ) ( − ) means that the actual direction is opposite to the assumed working direction. (b) Choose the location of the rotation axis; in other words, choose the pivot point with respect to which you will compute torques of acting forces. On the free-body diagram, indicate the location of the pivot and the lever arms of acting forces—you will need this for correct computations of torques. In the selection of the pivot, keep in mind that the pivot can be placed anywhere you wish, but the guiding principle is that the best choice will simplify as much as possible the calculation of the net torque along the rotation axis.
Set up the equations of equilibrium for the object. (a) Use the free-body diagram to write a correct equilibrium condition Equation 12.7 for force components in the x -direction. (b) Use the free-body diagram to write a correct equilibrium condition Equation 12.11 for force components in the y -direction. (c) Use the free-body diagram to write a correct equilibrium condition Equation 12.9 for torques along the axis of rotation. Use Equation 12.10 to evaluate torque magnitudes and senses.
Simplify and solve the system of equations for equilibrium to obtain unknown quantities. At this point, your work involves algebra only. Keep in mind that the number of equations must be the same as the number of unknowns. If the number of unknowns is larger than the number of equations, the problem cannot be solved.
Evaluate the expressions for the unknown quantities that you obtained in your solution. Your final answers should have correct numerical values and correct physical units. If they do not, then use the previous steps to track back a mistake to its origin and correct it. Also, you may independently check for your numerical answers by shifting the pivot to a different location and solving the problem again, which is what we did in Example 12.1 .

Note that setting up a free-body diagram for a rigid-body equilibrium problem is the most important component in the solution process. Without the correct setup and a correct diagram, you will not be able to write down correct conditions for equilibrium. Also note that a free-body diagram for an extended rigid body that may undergo rotational motion is different from a free-body diagram for a body that experiences only translational motion (as you saw in the chapters on Newton’s laws of motion). In translational dynamics, a body is represented as its CM, where all forces on the body are attached and no torques appear. This does not hold true in rotational dynamics, where an extended rigid body cannot be represented by one point alone. The reason for this is that in analyzing rotation, we must identify torques acting on the body, and torque depends both on the acting force and on its lever arm. Here, the free-body diagram for an extended rigid body helps us identify external torques.

Example 12.3

The torque balance.

w 1 = m 1 g w 1 = m 1 g is the weight of mass m 1 ; m 1 ; w 2 = m 2 g w 2 = m 2 g is the weight of mass m 2 ; m 2 ;

w = m g w = m g is the weight of the entire meter stick; w 3 = m 3 g w 3 = m 3 g is the weight of unknown mass m 3 ; m 3 ;

F S F S is the normal reaction force at the support point S .

We choose a frame of reference where the direction of the y -axis is the direction of gravity, the direction of the x -axis is along the meter stick, and the axis of rotation (the z -axis) is perpendicular to the x -axis and passes through the support point S . In other words, we choose the pivot at the point where the meter stick touches the support. This is a natural choice for the pivot because this point does not move as the stick rotates. Now we are ready to set up the free-body diagram for the meter stick. We indicate the pivot and attach five vectors representing the five forces along the line representing the meter stick, locating the forces with respect to the pivot Figure 12.10 . At this stage, we can identify the lever arms of the five forces given the information provided in the problem. For the three hanging masses, the problem is explicit about their locations along the stick, but the information about the location of the weight w is given implicitly. The key word here is “uniform.” We know from our previous studies that the CM of a uniform stick is located at its midpoint, so this is where we attach the weight w , at the 50-cm mark.

Now we can find the five torques with respect to the chosen pivot:

The second equilibrium condition (equation for the torques) for the meter stick is

When substituting torque values into this equation, we can omit the torques giving zero contributions. In this way the second equilibrium condition is

Selecting the + y + y -direction to be parallel to F → S , F → S , the first equilibrium condition for the stick is

Substituting the forces, the first equilibrium condition becomes

We solve these equations simultaneously for the unknown values m 3 m 3 and F S . F S . In Equation 12.17 , we cancel the g factor and rearrange the terms to obtain

To obtain m 3 m 3 we divide both sides by r 3 , r 3 , so we have

To find the normal reaction force, we rearrange the terms in Equation 12.18 , converting grams to kilograms:

Significance

Check your understanding 12.3.

Repeat Example 12.3 using the left end of the meter stick to calculate the torques; that is, by placing the pivot at the left end of the meter stick.

In the next example, we show how to use the first equilibrium condition (equation for forces) in the vector form given by Equation 12.7 and Equation 12.8 . We present this solution to illustrate the importance of a suitable choice of reference frame. Although all inertial reference frames are equivalent and numerical solutions obtained in one frame are the same as in any other, an unsuitable choice of reference frame can make the solution quite lengthy and convoluted, whereas a wise choice of reference frame makes the solution straightforward. We show this in the equivalent solution to the same problem. This particular example illustrates an application of static equilibrium to biomechanics.

Example 12.4

Forces in the forearm.

Notice that in our frame of reference, contributions to the second equilibrium condition (for torques) come only from the y -components of the forces because the x -components of the forces are all parallel to their lever arms, so that for any of them we have sin θ = 0 sin θ = 0 in Equation 12.10 . For the y -components we have θ = ± 90 ° θ = ± 90 ° in Equation 12.10 . Also notice that the torque of the force at the elbow is zero because this force is attached at the pivot. So the contribution to the net torque comes only from the torques of T y T y and of w y . w y .

and the y -component of the net force satisfies

Equation 12.21 and Equation 12.22 are two equations of the first equilibrium condition (for forces). Next, we read from the free-body diagram that the net torque along the axis of rotation is

Equation 12.23 is the second equilibrium condition (for torques) for the forearm. The free-body diagram shows that the lever arms are r T = 1.5 in . r T = 1.5 in . and r w = 13.0 in . r w = 13.0 in . At this point, we do not need to convert inches into SI units, because as long as these units are consistent in Equation 12.23 , they cancel out. Using the free-body diagram again, we find the magnitudes of the component forces:

We substitute these magnitudes into Equation 12.21 , Equation 12.22 , and Equation 12.23 to obtain, respectively,

When we simplify these equations, we see that we are left with only two independent equations for the two unknown force magnitudes, F and T , because Equation 12.21 for the x -component is equivalent to Equation 12.22 for the y -component. In this way, we obtain the first equilibrium condition for forces

and the second equilibrium condition for torques

The magnitude of tension in the muscle is obtained by solving Equation 12.25 :

The force at the elbow is obtained by solving Equation 12.24 :

The negative sign in the equation tells us that the actual force at the elbow is antiparallel to the working direction adopted for drawing the free-body diagram. In the final answer, we convert the forces into SI units of force. The answer is

The second equilibrium condition, τ T + τ w = 0 , τ T + τ w = 0 , can be now written as

From the free-body diagram, the first equilibrium condition (for forces) is

Equation 12.26 is identical to Equation 12.25 and gives the result T = 433.3 lb . T = 433.3 lb . Equation 12.27 gives

We see that these answers are identical to our previous answers, but the second choice for the frame of reference leads to an equivalent solution that is simpler and quicker because it does not require that the forces be resolved into their rectangular components.

Check Your Understanding 12.4

Repeat Example 12.4 assuming that the forearm is an object of uniform density that weighs 8.896 N.

Example 12.5

A ladder resting against a wall.

the net force in the y -direction is

and the net torque along the rotation axis at the pivot point is

where τ w τ w is the torque of the weight w and τ F τ F is the torque of the reaction F . From the free-body diagram, we identify that the lever arm of the reaction at the wall is r F = L = 5.0 m r F = L = 5.0 m and the lever arm of the weight is r w = L / 2 = 2.5 m . r w = L / 2 = 2.5 m . With the help of the free-body diagram, we identify the angles to be used in Equation 12.10 for torques: θ F = 180 ° − β θ F = 180 ° − β for the torque from the reaction force with the wall, and θ w = 180 ° + ( 90 ° − β ) θ w = 180 ° + ( 90 ° − β ) for the torque due to the weight. Now we are ready to use Equation 12.10 to compute torques:

We substitute the torques into Equation 12.30 and solve for F : F :

We obtain the normal reaction force with the floor by solving Equation 12.29 : N = w = 400.0 N . N = w = 400.0 N . The magnitude of friction is obtained by solving Equation 12.28 : f = F = 150.7 N . f = F = 150.7 N . The coefficient of static friction is μ s = f / N = 150.7 / 400.0 = 0.377 . μ s = f / N = 150.7 / 400.0 = 0.377 .

The net force on the ladder at the contact point with the floor is the vector sum of the normal reaction from the floor and the static friction forces:

Its magnitude is

and its direction is

We should emphasize here two general observations of practical use. First, notice that when we choose a pivot point, there is no expectation that the system will actually pivot around the chosen point. The ladder in this example is not rotating at all but firmly stands on the floor; nonetheless, its contact point with the floor is a good choice for the pivot. Second, notice when we use Equation 12.10 for the computation of individual torques, we do not need to resolve the forces into their normal and parallel components with respect to the direction of the lever arm, and we do not need to consider a sense of the torque. As long as the angle in Equation 12.10 is correctly identified—with the help of a free-body diagram—as the angle measured counterclockwise from the direction of the lever arm to the direction of the force vector, Equation 12.10 gives both the magnitude and the sense of the torque. This is because torque is the vector product of the lever-arm vector crossed with the force vector, and Equation 12.10 expresses the rectangular component of this vector product along the axis of rotation.

Check Your Understanding 12.5

For the situation described in Example 12.5 , determine the values of the coefficient μ s μ s of static friction for which the ladder starts slipping, given that β β is the angle that the ladder makes with the floor.

Example 12.6

Forces on door hinges.

We select the pivot at point P (upper hinge, per the free-body diagram) and write the second equilibrium condition for torques in rotation about point P :

We use the free-body diagram to find all the terms in this equation:

In evaluating sin β , sin β , we use the geometry of the triangle shown in part (a) of the figure. Now we substitute these torques into Equation 12.32 and compute B x : B x :

Therefore the magnitudes of the horizontal component forces are A x = B x = 100.0 N . A x = B x = 100.0 N . The forces on the door are

The forces on the hinges are found from Newton’s third law as

Check Your Understanding 12.6

Solve the problem in Example 12.6 by taking the pivot position at the center of mass.

Check Your Understanding 12.7

A 50-kg person stands 1.5 m away from one end of a uniform 6.0-m-long scaffold of mass 70.0 kg. Find the tensions in the two vertical ropes supporting the scaffold.

Check Your Understanding 12.8

A 400.0-N sign hangs from the end of a uniform strut. The strut is 4.0 m long and weighs 600.0 N. The strut is supported by a hinge at the wall and by a cable whose other end is tied to the wall at a point 3.0 m above the left end of the strut. Find the tension in the supporting cable and the force of the hinge on the strut.

As an Amazon Associate we earn from qualifying purchases.

This book may not be used in the training of large language models or otherwise be ingested into large language models or generative AI offerings without OpenStax's permission.

Want to cite, share, or modify this book? This book uses the Creative Commons Attribution License and you must attribute OpenStax.

Access for free at https://openstax.org/books/university-physics-volume-1/pages/1-introduction

Authors: William Moebs, Samuel J. Ling, Jeff Sanny
Publisher/website: OpenStax
Book title: University Physics Volume 1
Publication date: Sep 19, 2016
Location: Houston, Texas
Book URL: https://openstax.org/books/university-physics-volume-1/pages/1-introduction
Section URL: https://openstax.org/books/university-physics-volume-1/pages/12-2-examples-of-static-equilibrium

© Jan 19, 2024 OpenStax. Textbook content produced by OpenStax is licensed under a Creative Commons Attribution License . The OpenStax name, OpenStax logo, OpenStax book covers, OpenStax CNX name, and OpenStax CNX logo are not subject to the Creative Commons license and may not be reproduced without the prior and express written consent of Rice University.

Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies

Solved example problems for equilibrium of rigid bodies.

Solved Example Problems for Equilibrium

Example 5.12

Arun and Babu carry a wooden log of mass 28 kg and length 10 m which has almost uniform thickness. They hold it at 1 m and 2 m from the ends respectively. Who will bear more weight of the log? [g = 10 ms -2 ]

Let us consider the log is in mechanical equilibrium. Hence, the net force and net torque on the log must be zero. The gravitational force acts at the center of mass of the log downwards. It is cancelled by the normal reaction forces R A and R B applied upwards by Arun and Babu at points A and B respectively. These reaction forces are the weights borne by them.

The total weight, W = mg = 28 × 10 = 280 N, has to be borne by them together. The reaction forces are the weights borne by each of them separately. Let us show all the forces acting on the log by drawing a free body diagram of the log.

For translational equilibrium:

The net force acting on the log must be zero.

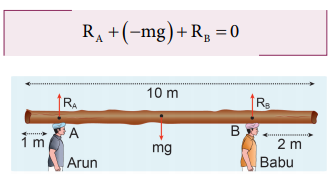
Here, the forces R A an R B are taken positive as they act upward. The gravitational force acting downward is taken negative.

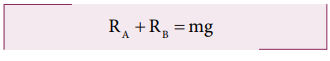
For rotational equilibrium:

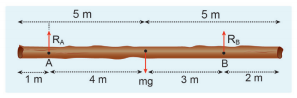
The net torque acting on the log must be zero. For ease of calculation, we can take the torque caused by all the forces about the point A on the log. The forces are perpendicular to the distances. Hence,

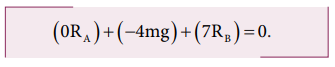
Here, the reaction force R A cannot produce any torque as the reaction forces pass through the point of reference A. The torque of force mg produces a clockwise turn about the point A which is taken negative and torque of force R B causes anticlockwise turn about A which is taken positive.

As R B is greater than R A , it is concluded that Babu bears more weight than Arun. The one closer to center of mass of the log bears more weight.

4.3 Rigid Body Equilibrium Equations

We use the equilibrium equations to calculate any unknown forces & moments using the known forces and values, and the following equations:

The particle equilibrium equations were covered in section 2.3. These are:

$$ \Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma F_{z}=0 $$

Now for a rigid body where forces are analyzed at different points on a body, we can take moments into account. There are 3 equations for 2d and 4 equations for 3d:

Rigid Body-Two Dimensions $$ \Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma M_{O}=0 $$ Rigid Body-Three Dimensions $$ \begin{gathered} \Sigma F_{x}=0, \Sigma F_{y}=0, \Sigma F_{z}=0 \\ \Sigma M_{x^{\prime}}=0, \Sigma M_{y^{\prime}}=0, \Sigma M_{z^{\prime}}=0 \end{gathered} $$

Because these are static bodies, the right side of the equations equal 0. In dynamics, they will equal the mass times the acceleration for translation and rotation.

For a rigid body in static equilibrium, that is a non-deformable body where forces are not concurrent, the sum of both the forces and the moments acting on the body must be equal to zero. The addition of moments (as opposed to particles where we only looked at the forces) adds another set of possible equilibrium equations, allowing us to solve for more unknowns as compared to particle problems.

Moments, like forces, are vectors. This means that our vector equation needs to be broken down into scalar components before we can solve the equilibrium equations. In a two dimensional problem, the body can only have clockwise or counter clockwise rotation (corresponding to rotations about the z axis). This means that a rigid body in a two dimensional problem has three possible equilibrium equations; that is, the sum of force components in the x and y directions, and the moments about the z axis. The sum of each of these will be equal to zero.

For a two dimensional problem, we break our one vector force equation into two scalar component equations.

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0$$

The one moment vector equation becomes a single moment scalar equation.

$$\sum\vec M=0\\\sum M_z=0$$

If we look at a three dimensional problem we will increase the number of possible equilibrium equations to six. There are three equilibrium equations for force, where the sum of the components in the x, y, and z direction must be equal to zero. The body may also have moments about each of the three axes. The second set of three equilibrium equations states that the sum of the moment components about the x, y, and z axes must also be equal to zero.

We break the forces into three component equations

$$\sum\vec F=0\\\sum F_x=0\:\sum F_y=0\:\sum F_z=0$$

We break the moments into three component equations

$$\sum\vec M=0\\\sum M_x=0\:\sum M_y=0\:\sum M_z=0$$

Finding the Equilibrium Equations:

As with particles, the first step in finding the equilibrium equations is to draw a free body diagram of the body being analyzed. This diagram should show all the force vectors acting on the body. In the free body diagram, provide values for any of the known magnitudes, directions, and points of application for the force vectors and provide variable names for any unknowns (either magnitudes, directions, or distances).

Next you will need to choose the x, y, z axes. These axes do need to be perpendicular to one another, but they do not necessarily have to be horizontal or vertical. If you choose coordinate axes that line up with some of your force vectors you will simplify later analysis.

Once you have chosen axes, you need to break down all of the force vectors into components along the x, y and z directions (see the vectors page in Appendix 1 page for more details on this process). Your first equation will be the sum of the magnitudes of the components in the x direction being equal to zero, the second equation will be the sum of the magnitudes of the components in the y direction being equal to zero, and the third (if you have a 3D problem) will be the sum of the magnitudes in the z direction being equal to zero.

Next you will need to come up with the the moment equations. To do this you will need to choose a point to take the moments about. Any point should work, but it is usually advantageous to choose a point that will decrease the number of unknowns in the equation. Remember that any force vector that travels through a given point will exert no moment about that point. To write out the moment equations simply sum the moments exerted by each force (adding in pure moments shown in the diagram) about the given point and the given axis (x, y, or z) and set that sum equal to zero. All moments will be about the z axis for two dimensional problems, though moments can be about x, y and z axes for three dimensional problems.

Once you have your equilibrium equations, you can solve these formulas for unknowns. The number of unknowns that you will be able to solve for will again be the number or equations that you have.

Source: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/3_equilibrium_rigid_body/3-6_equilibrium_equations_rigid_body/equilibrium_equations_rigid_body.html

Here is a visual example of using the equilibrium equations:

If we only consider the y (vertical) direction, the 200 lbs pushing down on the beam must be balanced by the reaction forces pushing up. The two reaction forces are equivalent because the forces on top are balanced evenly between the reaction forces. If they are at different locations, we use the sum of the moments equation and the distances of the people to determine the size of the reaction forces.

The car below has a mass of 1500 lbs with the center of mass 4 ft behind the front wheels of the car. What are the normal forces on the front and the back wheels of the car?

Source: Engineering Mechanics, Jacob Moore et al., http://mechanicsmap.psu.edu/websites/3_equilibrium_rigid_body/3-6_equilibrium_equations_rigid_body/pdf/EquilibriumEquationsExtended_WorkedProblem1.pdf

While sitting in a chair, a person exerts the forces in the diagram below. Determine all forces acting on the chair at points A and B. (Assume A is frictionless and B is a rough surface).

Key Takeaways

Basically: The equilibrium equations for rigid bodies are a way to determine unknown forces and moments using known forces and moments, separating the motion in 2 (or 3) directions for translation and rotation. Moments could be calculated because rigid bodies also consider shape and length.

Application: Calculate the reaction forces from the combined weight of an object.

Looking Ahead: This method will be used extensively in Ch 5 and 6.

Engineering Mechanics: Statics Copyright © by Libby (Elizabeth) Osgood; Gayla Cameron; Emma Christensen; Analiya Benny; and Matthew Hutchison is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

Sample Problems

Last updated
Save as PDF
Page ID 63408

Tom Weideman
University of California, Davis

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

All of the problems below have had their basic features discussed in an "Analyze This" box in this chapter. This means that the solutions provided here are incomplete, as they will refer back to the analysis performed for information (i.e. the full solution is essentially split between the analysis earlier and details here). If you have not yet spent time working on (not simply reading!) the analysis of these situations, these sample problems will be of little benefit to your studies.

Problem 5.1

A bug stands on the outer edge of a turntable as it begins to spin, accelerating rotationally in the horizontal plane from rest at a constant rate. The bug is held on the turntable by static friction, but as the turntable spins ever faster, this will not remain the case forever. The turntable, which has a radius of $0.40m$, has its rotational speed increase at a steady rate from rest, and reaches a speed of $\omega_1=1.2\frac{rad}{s}$ after its first full revolution.

Find the linear speed of the bug after the turntable makes $n$ full revolutions.
Find the coefficient of static friction if the bug falls off after the turntable makes $n$ full revolutions.

a. In the analysis , we indicated a kinematics relationship between $\alpha$, $\theta$, and $\omega$. The angular acceleration is constant, so it does not depend on the number of revolutions, and for $n$ revolutions, $\theta=2\pi n$, so the angular velocity after $n$ revolutions is:

\[\omega_n^2=2\alpha\left(2\pi n\right)=\omega_1^2 n\;\;\;\Rightarrow\;\;\;\omega_n=\omega_1\sqrt{n}\nonumber\]

The linear speed is the angular speed multiplied by the radius, so:

\[v_n=r\omega_n=r\omega_1\sqrt{n}=\left(0.40m\right)\left(1.2\frac{rad}{s}\right)\sqrt{n}=\left(0.48\frac{m}{s}\right)\sqrt{n}\nonumber\]

b. In the analysis we derived a formula for the coefficient of static friction in terms of the angular velocity and acceleration. Incorporating what we found above in terms of the number of full revolutions, we get:

\[\mu_s=\frac{r\sqrt{\omega_n^4+\alpha^2}}{g}=\frac{r\sqrt{n^2\omega_1^4+\left(\frac{\omega_1^2}{4\pi }\right)^2}}{g}=\frac{r\omega_1^2}{g}\sqrt{n^2+\frac{1}{16\pi^2}}=0.059\sqrt{n^2+0.0063}\nonumber\]

Notice that unless the angular acceleration is very large so that the bug falls off very quickly – in much less than a full revolution ($n\ll 1$) – virtually all of the static friction force goes into maintaining the centripetal acceleration, and only a very tiny fraction of the total static friction is involved with speeding up the bug.

Problem 5.2

The Blort Corporation makes a special widget that consists of a uniform disk pivoted around an axle at the end of a rod of negligible mass, which in turn rotates about its other end. This widget has two settings: It can be set in the "locked" position so that the disk does not rotate around its axle, or the "free" position so that the disk rotates frictionlessly about the axle. The difference these settings have on the motion of the disk as the rod rotates is depicted in the figure below.

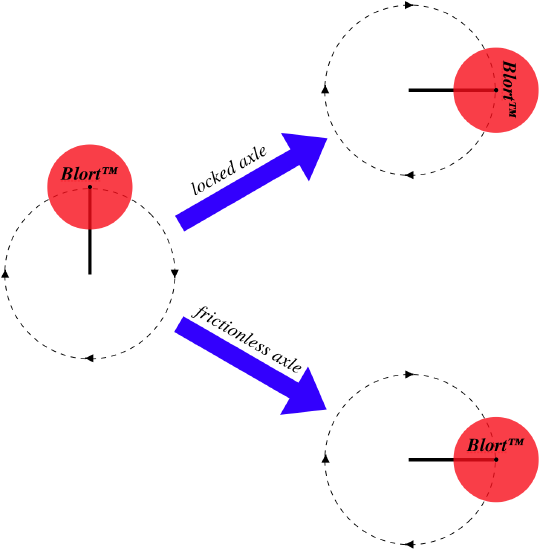
An engineer for a company that uses the Blort widgets in their manufacturing wants to make sure that the power output of the motor that turns the rod automatically adjusts so that the rod's rotation is the same whether the axle is in the fixed or free setting. The specifications of the widget indicates that the rod's length is equal to the diameter of the disk. By what factor must the power output of the motor be adjusted between these two settings?

In the analysis , we calculated the kinetic energies for a given rotational speed for each of these settings. The power from the motor goes directly into the kinetic energy of the widget, so the ratio of the kinetic energies will match the ratio of the power outputs:

\[\frac{P_{locked}}{P_{free}}=\frac{ {KE}_{locked}}{ {KE}_{free}} = \dfrac{\frac{1}{4}M\left(R^2+2L^2\right)\omega^2}{\frac{1}{2}ML^2\omega^2} = 1+\frac{1}{2}\left(\frac{R}{L}\right)^2\nonumber\]

The length of the rod is the diameter of the disk, so it is twice the radius, giving:

\[\frac{P_{locked}}{P_{free}} = 1.125\nonumber\]

Problem 5.3

A solid uniform sphere starts from rest and rolls down a flat ramp without slipping.

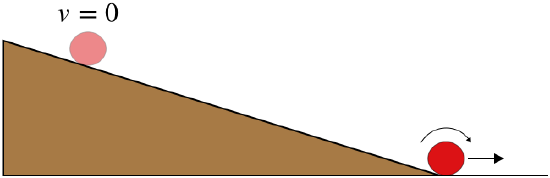
The sphere descends a vertical distance of $3.6m$ by the time it reaches the bottom, and it takes $6.6s$ to make the journey. Find the angle that the ramp makes with the horizontal.

We know the final speed of the sphere from our analysis :

\[v_f=\sqrt{\frac{10}{7}gh}\nonumber\]

The sphere started from rest, and as noted in the analysis, the acceleration is constant, so the average velocity is:

\[v_{ave}=\frac{v_o+v_f}{2}=\sqrt{\frac{5}{14}gh}\nonumber\]

This number, along with the time, gives us the straight-line (along the ramp) distance traveled by the ball:

\[d=v_{ave}t=\sqrt{\frac{5}{14}gh}\;t\nonumber\]

We now have the hypothenuse and opposite side of a right triangle, so we can get the angle:

\[\theta = \sin^{-1}\left(\frac{h}{d}\right)=\sin^{-1}\left(\sqrt{\frac{14h}{5gt^2}}\right)=\sin^{-1}\left(\sqrt{\frac{14\left(3.6m\right)}{5\left(9.8\frac{m}{s^2}\right)\left(6.6s\right)^2}}\right)=8.8^o\nonumber\]

Problem 5.4

A solid and a hollow sphere roll without slipping simultaneously (one behind the other) down a ramp and around a loop-de-loop. The radii of the spheres are negligible compared to the radius of the loop.

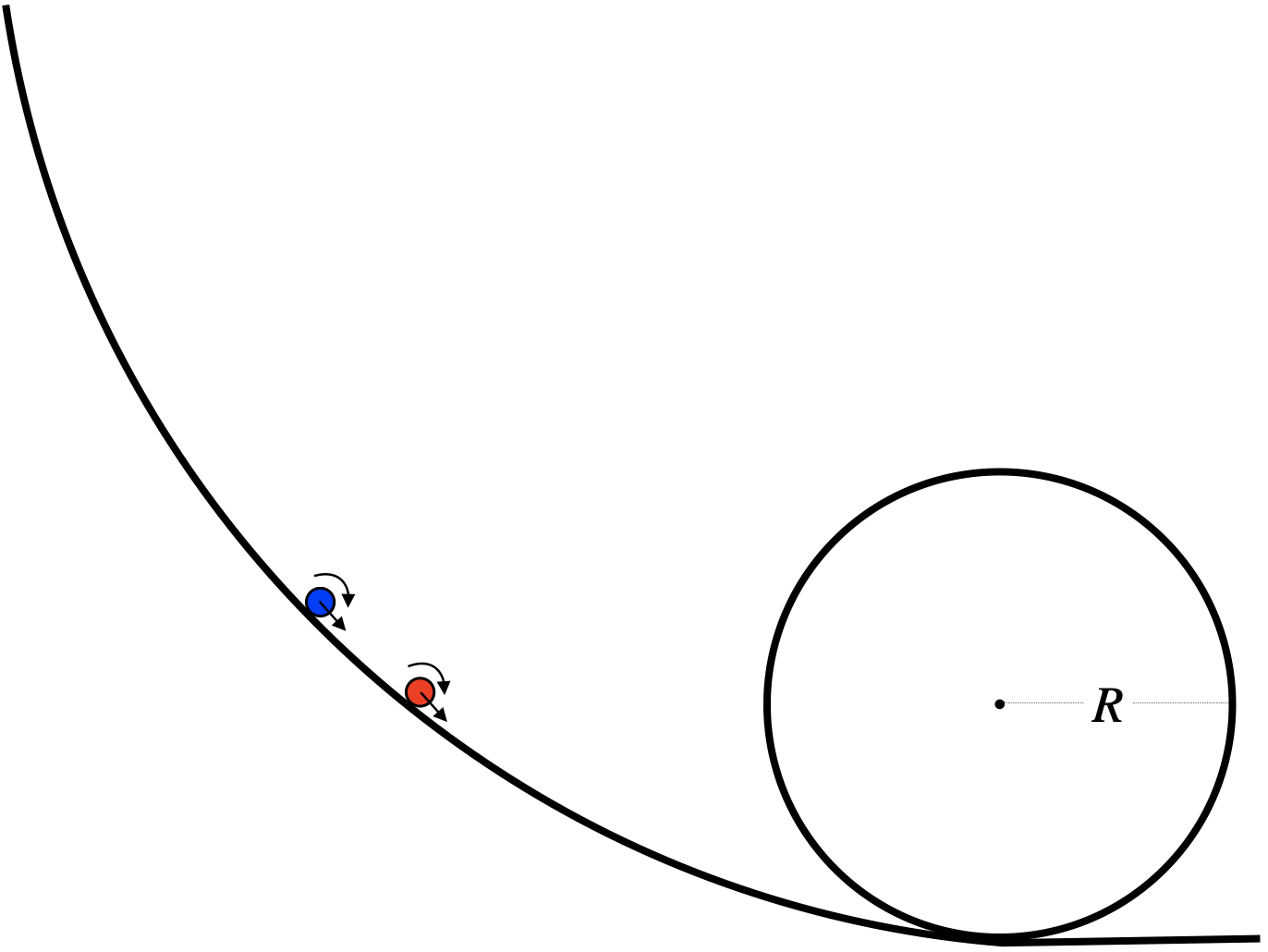
Both spheres are released simultaneously from rest, and both barely make it around the loop. Find which sphere is in front of the other, and the ratio of their starting heights.

In the analysis we found that if they have the same velocity, the two spheres will have different kinetic energies. We also found the speed either sphere must have in order to get all the way around the loop. Plugging this value into the kinetic energies of the spheres tells us how much kinetic energy they must have to make it around:

\[\left.\begin{array}{l} KE_{solid}=\frac{7}{10}mv^2 \\ v=\sqrt{gR} \end{array}\right\}\;\;\; KE_{solid}=\frac{7}{10}mgR\nonumber\]

\[\left.\begin{array}{l} KE_{hollow}=\frac{5}{6}mv^2 \\ v=\sqrt{gR} \end{array}\right\}\;\;\; KE_{solid}=\frac{5}{6}mgR\nonumber\]

Referencing zero gravitational potential energy at the bottom of the loop, at the top of the loop, the spheres alsoi have a potential energy of $2mgR$. Given that they start from rest, they start with only potential energy, so that equals their total energy:

\[E_{tot\;hollow}=mgh_{hollow}=mg\left(2R+\frac{5}{6}R\right)=\frac{17}{6}mgR\nonumber\]

\[E_{tot\;solid}=mgh_{solid}=mg\left(2R+\frac{7}{10}R\right)=\frac{27}{10}mgR\nonumber\]

The hollow sphere needs to start higher, and since they start simultaneously from rest, the leading sphere is the solid one. The ratio of their starting heights is:

\[\frac{h_{hollow}}{h_{solid}} = \frac{85}{81}\nonumber\]

Problem 5.5

One end of a massless rope is wound around a uniform solid cylinder, while the other end passes over a massless, frictionless pulley and is attached to a hanging block, as in the diagram below. The block is released from rest, pulling the cylinder along the horizontal surface such that it rolls without slipping.

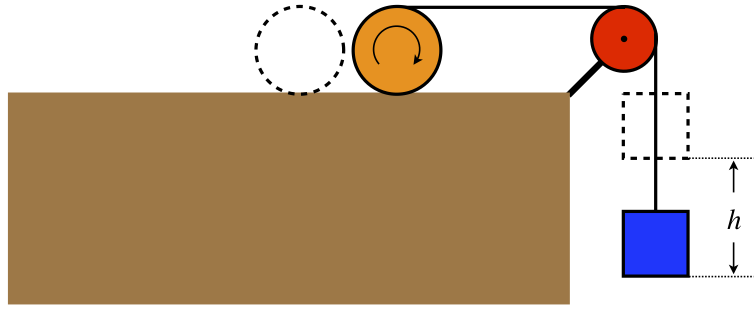
The cylinder and block are both weigh $22N$. Find the tension in the string.

In the analysis , we found the final velocity of the cylinder after the block drops a distance $h$. Plugging in equal masses for the block and cylinder gives, and solving for the velocity of the block using, $v_b=2v_c$:

\[v_f=2\sqrt{\frac{4m}{8m+3m}gh}=\sqrt{\frac{16}{11}gh}\nonumber\]

The acceleration of the block is constant, so from the kinematics equation with no time variable, we can get the acceleration:

\[v_f^2-v_o^2=2ay\;\;\;\Rightarrow\;\;\; a=\frac{v_f^2}{2h}=\frac{8}{11}g\nonumber\]

The acceleration is a result of the net force, which is the vector sum of the downward gravitational force and the upward tension force, so setting upward as the positive direction (making the acceleration negative), we get:

\[T-mg=ma\;\;\;\Rightarrow\;\;\;T=m\left(g+a\right)=m\left(g-\frac{8}{11}g\right)=\frac{3}{11}mg=\frac{3}{11}\left(22N\right)=6N\nonumber\]

Problem 5.6

Two disks are cut out of the same material, as shown in the diagram below. They are pivoted around stationary axles such that the two disks lie in the vertical plane, with their outer rims pinching a massless rope between them. The rope is pulled downward, causing both disks to turn without the rope slipping.

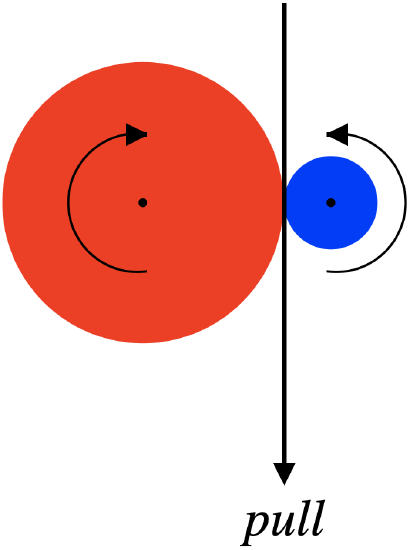
The smaller disk has one-third the radius of the larger disk. As the rope is pulled, power is delivered to the two-disk system. Find the fraction of the total power delivered to the larger disk.

To find the fraction of the power delivered, we only need to figure out the ratio of the energy of the small disk to the large disk at a given speed. This ratio is:

\[\frac{ {KE}_{small}}{ {KE}_{large}}=\dfrac{\frac{1}{2}I_{small}\omega_{small}^2}{\frac{1}{2}I_{large}\omega_{large}^2}=\left(\frac{I_{small}}{I_{large}}\right)\left(\frac{\omega_{small}}{\omega_{large}}\right)^2\nonumber\]

We found these ratios in terms of the ratios of the radii of the disks in the analysis .

\[\left.\begin{array}{l} \frac{I_{small}}{I_{large}}=\left(\frac{r}{R}\right)^4 \\ \frac{\omega_{small}}{\omega_{large}}=\frac{R}{r} \end{array}\right\} \;\;\; \frac{ {KE}_{small}}{ {KE}_{large}}= \left(\frac{r}{R}\right)^2=\left(\frac{1}{3}\right)^2=\frac{1}{9}\nonumber\]

Nine times as much power goes to the large disk as the small disk, which means that 90% of the total power delivered by the pulled rope is going to the large disk.

Problem 5.7

One end of a uniform metal thin rod is welded to the outer edge of a metal disk. The masses of these two objects are the same, and the length of the rod is equal to the diameter of the disk. The disk is suspended on a frictionless axle positioned at its center, and the rod is released from rest from a horizontal orientation and allowed to swing down to the vertical position.

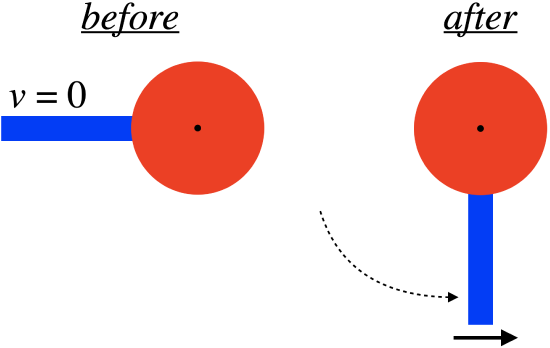
The linear speed of the open end of the rod at the bottom of the swing is measured to be $3.0\frac{m}{s}$. The pendulum is then removed from the axle and is swung in the same manner (from rest horizontally) with the open end of the rod now attached to the axle (so the disk is swinging down). Find the linear speed of the bottom edge of the disk when it gets to the bottom of the swing.

Let's start by using our result from the analysis to determine what is given. We know that the linear speed of the bottom of the rod is the angular velocity multiplied by the distance to the axle, so:

\[v_{rod\;end}=r\omega\;\;\;\Rightarrow\;\;\;3.0\frac{m}{s}=3R\omega_{rod\;swings}\nonumber\]

We can solve for the value of $R$ here, but as we will soon see, this is not necessary. We do, however, have to follow all the same steps from the analysis for the new setup. First, when pivoted at the open end of the rod, the center of mass of the whole object descends a distance of $2R$ (twice as far as the previous case), giving:

\[\Delta U = -2mg\left(2R\right)=-4mgR\nonumber\]

The moment of inertia also changes. This time we have the rod about its end and the disk extended by the parallel axis theorem:

\[I_{tot} = I_{rod}+I_{disk} = \frac{1}{3}m\left(2R\right)^2+\left[\frac{1}{2}mR^2+m\left(3R\right)^2\right] = \frac{65}{6}mR^2\nonumber\]

Putting this into the energy conservation gives:

\[{KE}_f=-\Delta U \;\;\;\Rightarrow\;\;\; \frac{1}{2}\left(\frac{65}{6}mR^2\right)\omega^2=4mgR\;\;\;\Rightarrow\;\;\; \omega=\sqrt{\frac{48g}{65R}}\nonumber\]

This is a bit slower than the previous case. The ratio of the two angular velocities are:

\[\frac{\omega_{disk\;swings}}{\omega_{rod\;swings}}=\sqrt{\frac{58}{65}}\nonumber\]

But we are interested in the linear velocity of the bottom of the disk. This is a distance of $4R$ from the axle, so using the result above, its linear velocity is:

\[v_{disk\;bottom}=4R\omega_{disk\;swings}=4R\left(\sqrt{\frac{58}{65}}\omega_{rod\;swings}\right)=\frac{4}{3}\sqrt{\frac{58}{65}}\left(3R\omega_{rod\;swings}\right)=\sqrt{\frac{928}{585}}\left(3.0\frac{m}{s}\right)=3.8\frac{m}{s}\nonumber\]

Problem 5.8

A small marble is attached to the end of a thin rigid rod with an equal mass, whose other end is held fixed at the origin. The rod starts at rest in the $x-y$ plane, and makes an angle $\theta$ up from the $x$-axis, as shown in the diagram. There is no gravity present, but the marble (not the rod) is subjected to a force from a potential energy field given by:

\[ U\left(x,y\right)=\beta x y+U_o \;,\;\;\;\; \beta=constant>0\nonumber \]

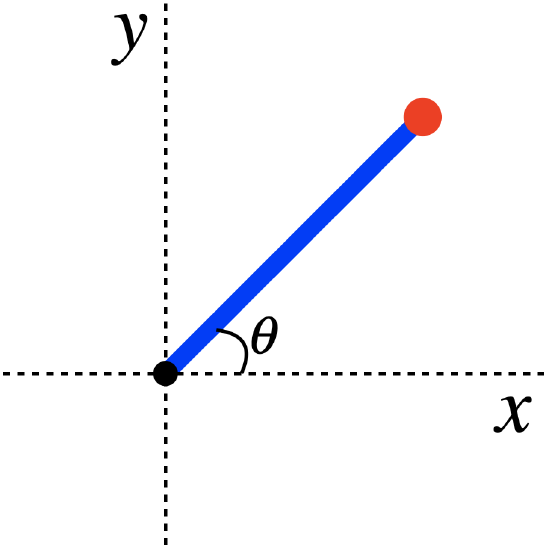
The values of the variables given above are:

\[\theta=30^o\;,\;\;\;\; \text{mass of marble}=0.45kg\;,\;\;\;\; \beta=1.2\frac{J}{m^2}\nonumber\]

Find the magnitude and direction of the angular acceleration when the rod is released. Express the direction of this acceleration both as a unit vector and as either clockwise or counterclockwise from the perspective of this diagram.
Find the maximum angular velocity attained by the rod, and the orientation angle of the rod when this maximum is reached.

a. As usual, most of the heavy-lifting in this problem was already done in the analysis . Using the expression for the angular acceleration derived in the analysis, we have:

\[\vec\alpha=-\frac{3\beta\cos2\theta}{4m}\;\hat k=-\frac{3\left(1.2\frac{J}{m^2}\right)\cos60^o}{4(0.45kg)}\;\hat k=-1.0\frac{rad}{s^2}\hat k\nonumber\]

This vector is in the $-\hat k$ direction, which points into the page, as we are using a right-handed coordinate system. From the RHR, this direction is clockwise from the perspective looking at the diagram.

b. Note that the linear velocity is a maximum when the rotational velocity is a maximum, so if we write the rotational velocity as a function of $\theta$, we just need to do calculus to find where the maximum occurs:

\[0=\frac{d\omega}{d\theta}=\frac{d\omega}{dt}\frac{dt}{d\theta}=\frac{\alpha}{\omega}\;\;\;\Rightarrow\;\;\;\alpha=0\nonumber\]

From the result for the angular acceleration, we see that the extrema occur at $\cos2\theta=0$, so $\theta = \pm 45^o$ or $\theta = \pm 135^o$. All of these angles satisfy $\left|x\right| = \left|y\right|.$ Next we need to determine which ones correspond to the maximum speed. Clearly the maximum kinetic energy occurs when the potential energy is a minimum, and looking at the potential energy function, this occurs when either $x$ or $y$ (but not both!) is negative. These two cases correspond to $\theta = -45^o$ and $\theta = 135^o$. The other two angles correspond to maximum potential energies, but since the marble starts with zero kinetic energy at a lower potential energy, it can never reach these points. Therefore the only place where the marble (which starts at $\theta=30^o$ and accelerates clockwise) can reach a maximum speed is $\theta=-45^o$.

Let's call the length of the rod $L$, as in the analysis. When the marble gets to $\theta=-45^o$, the potential energy is:

\[x=-y=\frac{1}{\sqrt 2}L;\;\;\Rightarrow\;\;\;U=-\frac{1}{2}\beta L^2+U_o\nonumber\]

Initially we had:

\[\left.\begin{array}{l}x=L\cos30^o=\frac{\sqrt 3}{2}L \\ y=L\sin30^o=\frac{1}{2}L \end{array}\right\} \;\;\;\;U=\frac{\sqrt 3}{4}\beta L^2+U_o\nonumber\]

The object starts from rest, so its final kinetic energy is just equal to the amount of potential energy lost:

\[KE=-\Delta U\;\;\;\Rightarrow\;\;\;\frac{1}{2}I_{tot}\omega^2=\left(\frac{\sqrt 3}{4}\beta L^2+U_o\right)-\left(-\frac{1}{2}\beta L^2+U_o\right)=\left(\frac{\sqrt 3+2}{4}\right)\beta L^2\nonumber\]

Plugging in for the moment of inertia of the whole object as found in the analysis, we get:

\[\frac{1}{2}\left(\frac{4}{3}mL^2\right)\omega^2=\left(\frac{\sqrt 3+2}{4}\right)\beta L^2\;\;\;\Rightarrow\;\;\;\omega = \sqrt{\frac{3}{8}\left(\sqrt 3+2\right)\left(\frac{1.2\frac{J}{m^2}}{0.45kg}\right)}=1.9\frac{rad}{s}\nonumber\]

Problem 5.9

Returning to the physical system of problem 5.6, we consider a new question. As before, the cylinder rolls without slipping, and the masses are equal (though here their exact values are not known).

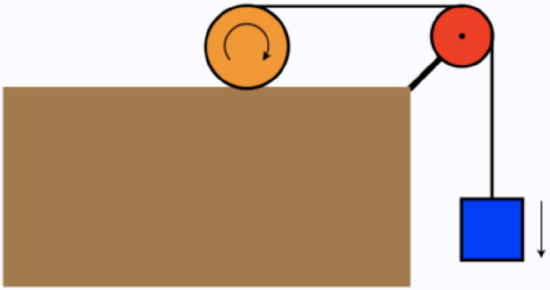
Find the minimum coefficient of static friction between the cylinder and the horizontal surface that will allow for this perfect rolling to occur.

In the analysis we wrote down the equations that come from Newton's 2nd Law (for linear and rotational motion), and found the accelerations of the cylinder and block. The if the cylinder is just barely rolling because the coefficient of friction is as low as it can be, that means that the largest possible static friction is occurring:

\[f=\mu_sN = m_smg\nonumber\]

Putting this into the $x$-direction equation for the cylinder from Newton's 2nd Law, and plugging in the tension in the rope and the acceleration (both found in the analysis) gives:

\[f+T=ma\;\;\;\Rightarrow\;\;\;\mu_smg=-\frac{3}{4}ma+ma=\frac{1}{4}ma=\frac{1}{4}m\left(\frac{4}{11}g\right)\;\;\;\Rightarrow\;\;\;\mu_s=\frac{1}{11}\nonumber\]

Problem 5.10

Two ends of a massless rope are wound around two spools with equal masses and radii. One of the spools is a solid, uniform disk, while the other is a thin, hollow cylinder. The rope between them goes over a massless, frictionless pulley in a vertical plane. The spools are released from rest from the same height, and the rope does not slip over the pulley.

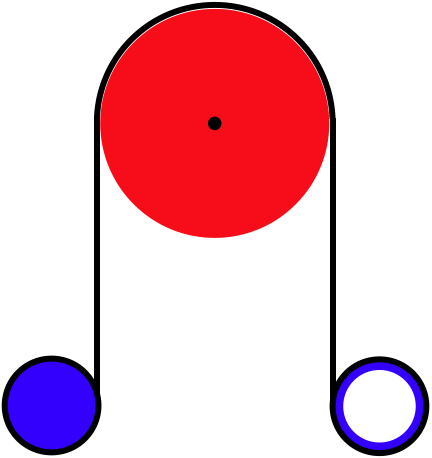
The radius of the pulley is $25cm$. Find the angle through which the pulley has turned when $2.0s$ has elapsed.

From the result in the analysis , we can compute how much additional rope is in play. It is simply twice the distance that the spools fall:

\[\Delta L = 2\Delta y = 2\left(\frac{1}{2}at^2\right)=\left(\frac{3}{5}g\right)t^2=\frac{3}{5}\left(9.8\frac{m}{s^2}\right)\left(2.0s\right)^2=23.5m\nonumber\]

The torques are the same on both spools, but the solid spool has one-half the moment of inertia of the hollow one, so it has twice the angular acceleration, which means that over the same time period, it loses twice as much rope. Let's call the amount of rope lost by the hollow spool $l$, so the amount lost by the solid spool is $2l$. The rotation of the pulley makes up for this difference, which means it takes $\frac{1}{2}l$ from the side where the solid spool is, and places it on the side of the hollow spool. Noting that the total rope lost by both spools combined is $3l=\Delta L$, and using the no-slipping condition, we have:

\[s=R\theta\;\;\;\Rightarrow\;\;\; \theta = \frac{s}{R}=\frac{\frac{1}{2}l}{R}=\frac{\Delta L}{6R}=\frac{23.52m}{6\left(0.25m\right)}=15.7rad\nonumber\]

Problem 5.11

A board starts at rest and is free of any attachments (it is not pivoted on anything). It is pushed in opposite directions on both of its ends with forces of equal magnitude, at right angles to the board. The forces continue to be applied at right angles with the same magnitude, causing the board to rotate in the manner depicted in the diagram until the board has rotated by $90^o$.

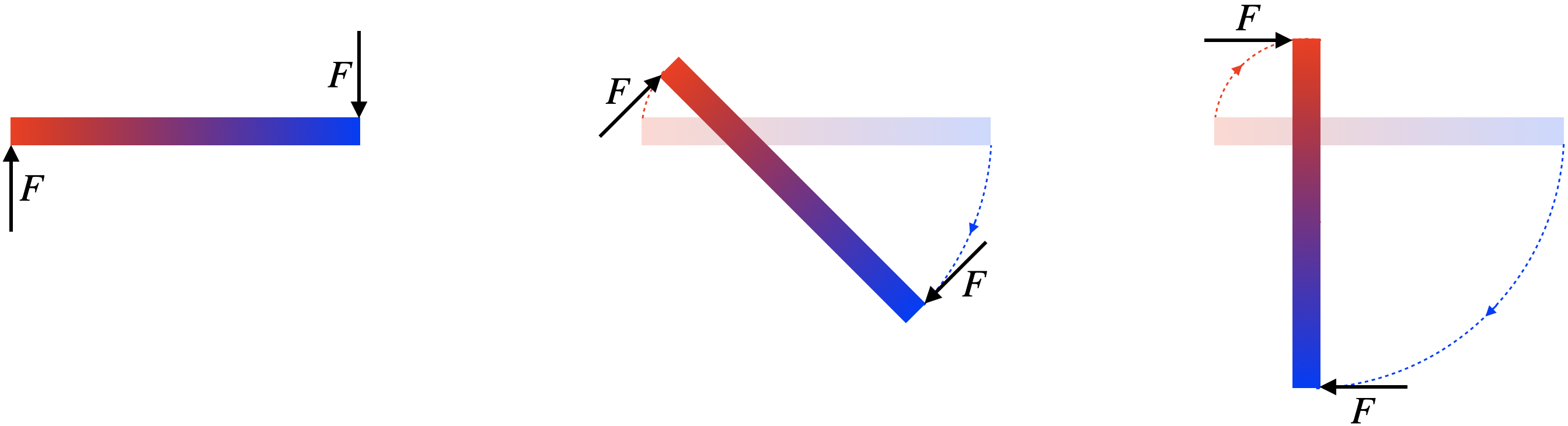
The time it takes the board to rotate the $90^o$ is $t$. Derive an expression for the moment of inertia of this board in terms of $ t$, the length of board $L$, and the force $F$.

The analysis showed us that wherever the center of mass happens to be, the torque applied is still equal to $FL$. Newton's 2nd Law for rotations gives:

\[\tau=I\alpha\;\;\;\Rightarrow\;\;\; I=\frac{\tau}{\alpha}=\frac{FL}{\alpha}\nonumber\]

The board starts from rest, and the torque remains constant, so it accelerates rotationally at a constant rate, which means its motion satisfies the usual kinematics equation:

\[\Delta\theta = \frac{1}{2}\alpha t^2\nonumber\]

We know that the rod rotates through an angle of $\frac{\pi}{2}$ radians, and we know the time elapsed is $t$, so we can solve for $\alpha$ and this gives our final answer:

\[\alpha = \frac{2\Delta\theta}{t^2}=\frac{\pi}{t^2}\;\;\;\Rightarrow\;\;\;I=\frac{FLt^2}{\pi}\nonumber\]

Problem 5.12

The blob in the figure below is rigid and in static equilibrium. The two forces shown are two of the total of three forces exerted on the object.

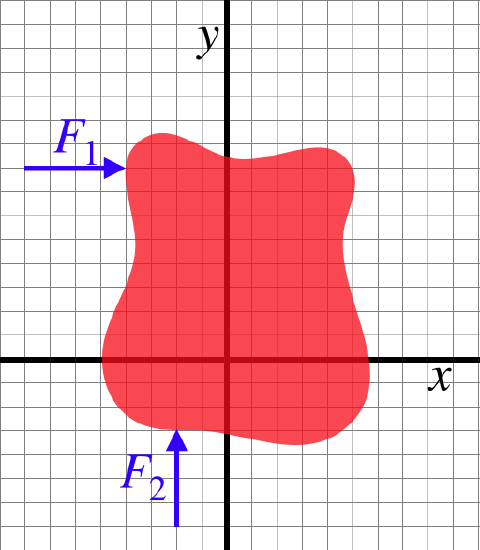
The magnitude of $F_1$ is three-quarters the magnitude of $F_2$. Find the equation of the line along which the third force acts.

For this object to remain in equilibrium, the net torque about every point in space must vanish. Consider the reference point $x=-2$, $y=+8$. Both of the given forces act through this point, so neither of them provides a torque around this reference point. There is only one more force present, and for the net torque around that reference point to be zero, the third force must also contribute zero torque, and this is only possible if that third force passes through the reference point.

In the analysis we found the tangent of the angle the force vector makes with the $x$-axis. This is the slope of the force line, and we are given the ratio of these two force magnitudes:

\[slope = \frac{F_2}{F_1} = \frac{4}{3}\nonumber\]

Now we know one point on the line and its slope, and these two quantities completely define it. Putting an arbitrary $\left(x,y\right)$ point and the reference point into the slope equation gives us the equation of the line:

\[\frac{4}{3}=slope=\frac{y-y_{ref}}{x-x_{ref}}=\frac{y-8}{x+2}\;\;\;\Rightarrow\;\;\;y=\frac{4}{3}x+\frac{32}{3}\nonumber\]

Problem 5.13

Two painters carry a plank of plywood that they use for scaffolding over their heads on their way to the job site. The plank has a uniform mass distribution. Atop the plank is a can of paint weighing one third as much as the plank. The painter in the rear is holding the plank at the very end and the painter in front is holding the plank one quarter of the the plank length from the front. The can of paint is two-fifths of the plank length from the front. The plank is horizontal as they carry it.

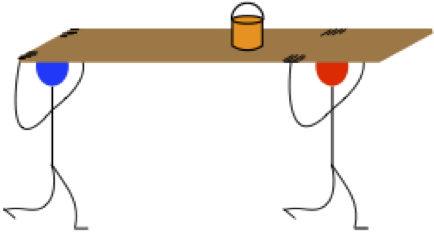
The can of paint weighs $50N$. Find how much force each painter is exerting on the plank.

As is typical for these types of problems, the analysis often solves the whole thing. In this case, we know that the plank weighs three times as much as the paint, so the total weight carried is $200N$. We found in the analysis how the load is distributed, so we have our answers already:

\[rear\;painter=0.30\left(200N\right)=60N\;,\;\;\;\;front\;painter=0.70\left(200N\right)=140N\nonumber\]

Problem 5.14

The diagram below depicts a yo-yo on an inclined plane with its string over a massless pulley and attached to a hanging block. The whole system is in static equilibrium.

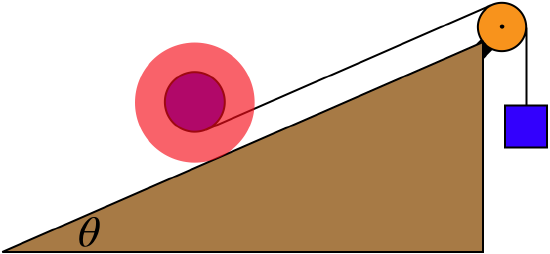
The inner radius of the yo-yo is half the outer radius, and the coefficient of friction is 0.40.

Find the maximum angle $\theta$ for which this system can be at static equilibrium (assume that the hanging mass can be adjusted to whatever is necessary).
The mass of the yo-yo is $0.35kg$. If the angle $\theta$ is at its maximum, find the hanging weight.

a. We have the equations of equilibrium from the analysis already. As the angle gets larger, the $F_y$ equation shows that the normal force on the yo-yo by the plane gets smaller. This reduces the value of the maximum static friction force available. When the angle is so great that the new maximum friction force equals the actual friction force, then making the angle any larger would cause the yo-yo to slip. So the maximum angle without slippage means that $f=\mu_sN$. Now we do some algebra.

Eliminate the tension first:

\[T=\frac{R}{r}f\;\;\;\Rightarrow\;\;\;\left(\frac{R}{r}-1\right)f-Mg\sin\theta=0\nonumber\]

Next eliminate the friction force:

\[f=\mu_sN\;\;\;\Rightarrow\;\;\;\left(\frac{R}{r}-1\right)\mu_sN-Mg\sin\theta=0\nonumber\]

And now the normal force:

\[N=Mg\cos\theta\;\;\;\Rightarrow\;\;\;\left(\frac{R}{r}-1\right)\mu_sMg\cos\theta-Mg\sin\theta=0\nonumber\]

Plugging-in the given $R=2r$ and solving for $\theta$ gives:

\[\theta = \tan^{-1}\mu_s=\tan^{-1}\left(0.4\right)=21.8^o\nonumber\]

b. Now to find the hanging mass, we need the tension. From the three equations above, we see that we can get the normal force from the mass of the yo-yo, the friction force from the normal force, and the tension from the friction:

\[mg=T=\frac{R}{r}f=\frac{R}{r}\mu_sN=\frac{R}{r}\mu_sMg\cos\theta\;\;\;\Rightarrow\;\;\;m=\left(2\right)\left(0.4\right)\left(0.35kg\right)\cos\left(21.8^o\right)\nonumber=0.26kg\]

Engineering Statics: Open and Interactive

Daniel W. Baker, William Haynes

Section 5.5 3D Rigid Body Equilibrium

Key questions.

What are the similarities and differences between solving two-dimensional and three-dimensional equilibrium problems?
Why are some three-dimensional reaction couple-moments “available but not engaged”?
What kinds of problems are solvable using linear algebra?

Resolving Forces and Moments into Components.

First, choose any point in the system to sum moments around.
Sum moments around each axis. For relatively simple systems with few position and force vector components, you can find the cross product for each non-parallel position and force pair. Using this method requires you to resolve the direction of each cross product pair using the right-hand rule as covered in Chapter 4 . Recall that there are up to six pairs of non-parallel components that you need to consider.
Sum all moments around a point using vector determinants. Choose a point in the system which is on the line of action of as many forces as possible, then set up each cross product as a determinant. After computing the components coming from each determinant, combine the $x\text{,}$ $y\text{,}$ and $z$ terms into each of the $\Sigma\vec{M}_x=0\text{,}$ $\Sigma\vec{M}_y=0\text{,}$ and $\Sigma\vec{M}_z=0$ equations.
Finally, add the components of any couple-moments into the corresponding $\Sigma\vec{M}_x=0\text{,}$ $\Sigma\vec{M}_y=0\text{,}$ and $\Sigma\vec{M}_z=0$ equations.

Solving for unknown values in equilibrium equations.

Three-dimensional equilibrium examples., example 5.5.1 . 3d bent bar..

Determine the force acting at point $A$ in Cartesian form. The force of the cable acts from $A$ to $B\text{.}$ This direction is described by the displacement vector from $A$ to $B$ \begin{equation*} \vec{r}_{AB} = \ft{(2 \ihat- 4 \jhat - 1 \khat )} \end{equation*} or the corresponding unit vector \begin{align*} \lambda_{AB} \amp = \frac{\vec{r}_{AB}}{\left|\vec{r}_{AB}\right|} \\ \amp = \frac{2 \ihat- 4 \jhat - 1 \khat}{\sqrt{(2)^2 + (-4)^2 + (-1)^2 }}\\ \amp = \frac{2 \ihat- 4 \jhat - 1 \khat}{\sqrt{21}} \text{.} \end{align*} Multiplying the unit vector by the cable tension gives the force acting on $A$ as a three-dimensional Cartesian force vector \begin{align*} \vec{F} \amp = \lambda_{AB} T \\ \amp = \left( \frac{2 \ihat - 4\jhat- 1 \khat}{\sqrt{21}} \right) \lb{500}\\ \amp = \left( 2 \ihat - 4\jhat- 1 \khat \right) \lb{\left(\frac{500}{\sqrt{21}}\right)} \end{align*} \begin{equation*} \vec{F} = \lb{(218 \ihat - 436 \jhat - 109 \khat)}\text{.} \end{equation*}
Determine the moment about $C$ . The moment about point $C$ is found with the cross product (4.3.4) where the moment arm is the displacement vector from $C$ to $A\text{.}$ \begin{equation*} \vec{r}_{CA} = \ft{(4 \ihat + 0 \jhat + 5 \khat )} \end{equation*} \begin{align*} \vec{M}_C \amp = \vec{r}_{CA} \times \vec{F} \\ \amp = \begin{vmatrix} \ihat \amp \jhat \amp \khat \\ 4 \amp 0 \amp 5 \\ 2 \amp -4 \amp -1 \\ \end{vmatrix} \left(\frac{500}{\sqrt{21}}\right) \end{align*} \begin{equation*} \vec{M}_C = \ftlb{(2182 \ihat + 1528 \jhat - 1746 \khat)} \end{equation*}
Apply the equations of equilibrium. \begin{align*} \Sigma \vec{F} \amp = 0 \qquad \begin{cases} \Sigma F_x = 0 : \amp C_x + F_x = 0 \\ \amp C_x = - \lb{218} \\ \Sigma T_y = 0 :\amp C_y - F_y = 0 \\ \amp C_y = + \lb{436} \\ \Sigma T_z = 0 : \amp C_z - F_z = 0 \\ \amp C_z = + \lb{109} \\ \end{cases} \\ \\ \Sigma \vec{M} \amp = 0 \qquad \begin{cases} \Sigma M_x = 0 :\amp M_x + {M_C}_x = 0 \\ \amp M_x = \ftlb{-2180} \\ \Sigma M_y = 0 : \amp M_y + {M_C}_y = 0 \\ \amp M_y = \ftlb{-1530} \\ \Sigma M_z = 0 : \amp M_z +{M_C}_z = 0 \\ \amp M_z = \ftlb{+1750} \\ \end{cases} \end{align*} The resulting vector equations for the reaction force $\vec{C}$ and reaction moment $\vec{M}$ are \begin{align*} \vec{C} \amp= \lb{(-218 \ihat + 436 \jhat + 109 \khat)}\\ \vec{M} \amp = \ftlb{(-2180 \ihat -1530 \jhat + 1750 \khat)}\text{.} \end{align*}

school Campus Bookshelves
menu_book Bookshelves
perm_media Learning Objects
login Login
how_to_reg Request Instructor Account
hub Instructor Commons

Margin Size

Download Page (PDF)
Download Full Book (PDF)
Periodic Table
Physics Constants
Scientific Calculator
Reference & Cite
Tools expand_more
Readability

selected template will load here

This action is not available.

5.5: 3D Rigid Body Equilibrium

Last updated
Save as PDF
Page ID 70237

Daniel W. Baker and William Haynes
Colorado State University via Engineeringstatics

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

Key Questions

What are the similarities and differences between solving two-dimensional and three-dimensional equilibrium problems?
Why are some three-dimensional reaction couple-moments “available but not engaged”?
What kinds of problems are solvable using linear algebra?

Three-dimensional systems are closer to reality than two-dimensional systems and the basic principles to solving both are the same, however they are generally harder solve because of the additional degrees of freedom involved and the difficulty visualizing and determining distances, forces and moments in three dimensions.

Three-dimensional problems are usually solved using vector algebra rather than the scalar approach used in the last section. The main differences are that directions are described with unit vectors rather than with angles, and moments are determined using the vector cross product rather scalar methods. Because they have more possible unknowns it is harder to find efficient equations to solve by hand. A problem might involve solving a system of up to six equations and six unknowns, in which case it is best solved using linear algebra and technology.

Resolving Forces and Moments into Components.

To break two-dimensional forces into components, you likely used right-triangle trigonometry, sine and cosine. However, three-dimensional forces will likely need to be broken into components using Section 2.5.

When summing moments, make sure to consider both the $\vec{r}\times\vec{F}$ moments and also the couple-moments with the following guidance:

First, choose any point in the system to sum moments around.
For relatively simple systems with few position and force vector components, you can find the cross product for each non-parallel position and force pair. Using this method requires you to resolve the direction of each cross product pair using the right-hand rule as covered in Chapter 4. Recall that there are up to six pairs of non-parallel components that you need to consider.
Choose a point in the system which is on the line of action of as many forces as possible, then set up each cross product as a determinant. After computing the components coming from each determinant, combine the $x\text{,}$ $y\text{,}$ and $z$ terms into each of the $\Sigma\vec{M}_x=0\text{,}$ $\Sigma\vec{M}_y=0\text{,}$ and $\Sigma\vec{M}_z=0$ equations.
Finally, add the components of any couple-moments into the corresponding $\Sigma\vec{M}_x=0\text{,}$ $\Sigma\vec{M}_y=0\text{,}$ and $\Sigma\vec{M}_z=0$ equations.

Solving for unknown values in equilibrium equations.

Once you have formulated $\Sigma\vec{F}=0$ and $\Sigma\vec{M}=0$ equations in each of the $x\text{,}$ $y$ and $z$ directions, you could be facing up to six equations and six unknown values.

Frequently these simultaneous equation sets can be solved with substitution, but it is often be easier to solve large equation sets with linear algebra. Note that the adjective “linear” specifies that the unknown values must be linear terms, which means that each unknown variable cannot be raised to a exponent, be an exponent, or buried inside of a $\sin$ or $\cos$ function. Luckily, most unknowns in equilibrium are linear terms, except for unknown angles. If you are not familiar with the use of linear algebra matrices to solve simultaneously equations, search the internet for Solving Systems of Equations Using Linear Algebra and you will find plenty of resources.

No matter how you choose to solve for the unknown values, any numeric values which come out to be negative indicate that your initial hypothesis of that vector’s sense was incorrect.

Three-dimensional Equilibrium Examples.

IMAGES

equilibrium of rigid bodies solved problems
equilibrium of rigid bodies solved problems
Equilibrium of Rigid Bodies (2D
Equilibrium of Rigid Bodies 3D force Systems
equilibrium of rigid bodies solved problems
5-65 Equilibrium of a Rigid Body (3D Equilibrium) Hibbeler Statics 14th Edition Engineers Academy

VIDEO

Solved examples; equilibrium of bodies
Solved examples; equilibrium of bodies
MECHANICS
(65) STATIC OF RIGID BODIES
Chapter 5 |Equilibrium of Rigid body |Part 5|Solved Problems |ENGINEERING MECHANICS Statics
Mechanics (Lecture 6): Equilibrium of Rigid Bodies

COMMENTS

3.6: Equilibrium Analysis for a Rigid Body
The one moment vector equation becomes a single moment scalar equation. ∑M = 0 (3.6.3) (3.6.3) ∑ M → = 0. ∑Mz = 0 (3.6.4) (3.6.4) ∑ M z = 0. If we look at a three-dimensional problem we will increase the number of possible equilibrium equations to six. There are three equilibrium equations for force, where the sum of the components in ...
PDF Chapter 5: Equilibrium of Rigid Bodies
The uniform truck ramp has weight 400 lb and is pinned to the body of the truck at each side and held in the position shown by the two side cables. Determine the reaction forces at the pins and the tension in the cables. The operator applies a vertical force to the pedal so that the spring is stretched 1.5 in. and the force in the short link at ...
Statics: 2D Rigid Body Equilibrium
5.4. 2D Rigid Body Equilibrium. Two-dimensional rigid bodies have three degrees of freedom, so they only require three independent equilibrium equations to solve. The six scalar equations of (5.3.3) can easily be reduced to three by eliminating the equations which refer to the unused \ (z\) dimension. For objects in the \ (xy\) plane there are ...
Rigid Body Equilibrium Problems
A rigid body is said to be in static equilibrium when the net force and the net torque acting on the system is equal to zero. To solve for rigid body equilibrium problems, do the following steps. Step 1: Identify the object to be analyzed and all forces acting on the object. In addition, identify the known and unknown variables in the given problem.
Engineering Statics: Open and Interactive
At its core, Engineering Statics provides the tools to solve static equilibrium problems for rigid bodies. The additional topics of resolving internal loads in rigid bodies and computing area moments of inertia are also included as stepping stones for later courses.
Rigid Body Equilibrium Problems
A rigid body is said to be in static equilibrium when the net force and the net torque acting on the system is equal to zero. To solve for rigid body equilibrium problems, do the following steps. Step 1: Identify the object to be analyzed and all forces acting on the object. In addition, identify the known and unknown variables in the given ...
Lesson Explainer: Equilibrium of a Rigid Body
A rigid body is in equilibrium if the sum of the forces and the sum of the moments on the body are zero. Consider a uniform rod of length 2 𝑙, negligible thickness, and weight 𝑊. The rod is suspended at one end by a rope that applies a tension 𝑇 vertically upward. The magnitudes of 𝑇 and 𝑊 are equal. The rod is in translational ...
12.2 Examples of Static Equilibrium
All examples in this chapter are planar problems. Accordingly, we use equilibrium conditions in the component form of Equation 12.7 to Equation 12.9.We introduced a problem-solving strategy in Example 12.1 to illustrate the physical meaning of the equilibrium conditions. Now we generalize this strategy in a list of steps to follow when solving static equilibrium problems for extended rigid bodies.
Solved Example Problems for Equilibrium of Rigid Bodies
Solved Example Problems for Equilibrium of Rigid Bodies. Physics : Motion of System of Particles and Rigid Bodies : Equilibrium. Solved Example Problems for Equilibrium. Example 5.12. Arun and Babu carry a wooden log of mass 28 kg and length 10 m which has almost uniform thickness. They hold it at 1 m and 2 m from the ends respectively.
4.3 Rigid Body Equilibrium Equations
For a rigid body in static equilibrium, that is a non-deformable body where forces are not concurrent, the sum of both the forces and the moments acting on the body must be equal to zero.The addition of moments (as opposed to particles where we only looked at the forces) adds another set of possible equilibrium equations, allowing us to solve for more unknowns as compared to particle problems.
Sample Problems
Problem 5.12. The blob in the figure below is rigid and in static equilibrium. The two forces shown are two of the total of three forces exerted on the object. The magnitude of $F_1$ is three-quarters the magnitude of $F_2$. Find the equation of the line along which the third force acts. Solution
Equilibrium of Rigid Bodies (2D
Learn to solve equilibrium problems in 2D (coplanar forces x - y plane). We talk about resultant forces, summation of forces in each direction and moments.🔹...
EQUILIBRIUM OF RIGID BODIES
The second condition of equilibrium applied to an axis perpendicular. to the paper at the hinge gives. E~ = T(sin e) L -(W)(L/2) - F(0.90)L = O. Solution of this last equation for T using the values of L, W, F, and e from the problem gives T = 450 N. The first two equations can then be solved to give.
Statics: 3D Rigid Body Equilibrium
5.4 2D Rigid Body Equilibrium. 5.5 3D Rigid Body Equilibrium. 5.6 Stability and Determinacy. 5.7 Equilibrium Examples. 5.8 Exercises (Ch. 5) 6 Equilibrium of Structures. ... Because they have more possible unknowns it is harder to find efficient equations to solve by hand. A problem might involve solving a system of up to six equations and six ...
4.17 Engineering Mechanics: Rigid body equilibrium (2D)
In this video we apply equilibrium conditions to a rigid body (2-dimensional) and determine the support reaction at the pin joint and the cable tension as w...
4.18 Engineering Mechanics: Rigid body equilibrium (2D)
In this video, two problems relating to equilibrium of two-dimensional rigid bodies are solved - the first involves 'collars sliding on fixed rods' and the s...
[Statics] Equilibrium of Rigid Bodies 2D Problems
Statics: Problem 5-32: Equilibrium of a Rigid body 2D. Mechanical Engineering with Dr. Sanei. 436. views. 03:18. Statics Example: 2D Rigid Body Equilibrium 2. UWMC Engineering. 563. ... How to Solve a 2D Equilibrium Problem - Step by Step Solution. AF Math & Engineering. 588. views. Showing 1 of 8 videos. Load more videos.
5: Rigid Body Equilibrium
The important difference between rigid bodies and the particles of Chapter 3 is that rigid bodies have the potential to rotate around a point or axis, while particles do not. For rigid body equilibrium, we need to maintain translational equilibrium with. ∑F = 0 (5.0.1) (5.0.1) ∑ F = 0. and also maintain a balance of rotational forces and ...
5.5: 3D Rigid Body Equilibrium
Solving for unknown values in equilibrium equations. Once you have formulated ΣF = 0 Σ F = 0 and ΣM = 0 Σ M = 0 equations in each of the x, x, y y and z z directions, you could be facing up to six equations and six unknown values. Frequently these simultaneous equation sets can be solved with substitution, but it is often be easier to solve ...

12.5: Rigid Body Equilibrium Problems - I

Get cutting-edge science videos from J o VE sent straight to your inbox every month.

Engineering Statics: Open and Interactive

Formats Available

Table of Contents

Ancillary Material

About the Book

About the Contributors

Contribute to this Page

12.2 Examples of Static Equilibrium

Problem-Solving Strategy

Example 12.3

Significance

Example 12.4

Check Your Understanding 12.4

Example 12.5

Check Your Understanding 12.5

Example 12.6

Check Your Understanding 12.6

Check Your Understanding 12.7

Check Your Understanding 12.8

Chapter: 11th Physics : UNIT 5 : Motion of System of Particles and Rigid Bodies

Example 5.12

For translational equilibrium:

For rotational equilibrium:

4.3 Rigid Body Equilibrium Equations

Finding the Equilibrium Equations:

Share This Book

Margin Size

Sample Problems

Engineering Statics: Open and Interactive

Section 5.5 3D Rigid Body Equilibrium

Resolving Forces and Moments into Components.

Solving for unknown values in equilibrium equations.

Margin Size

5.5: 3D Rigid Body Equilibrium

Resolving Forces and Moments into Components.

Solving for unknown values in equilibrium equations.

Three-dimensional Equilibrium Examples.

IMAGES

VIDEO

COMMENTS